Chapter 14: Practical Geometry

Introduction
Different different  geometrical shapes are made with the help of ruler or straight edge and compass. 
In this chapter we shall learn to make these shapes. In making these shapes we need to use some tools. So, we shall begin with listing these tools, describing them and looking at how they are used.

We are going to consider “Ruler and compasses constructions”, using ruler, only to draw lines, and compasses, only to draw arcs.

Chapter 14

Practical Geometry

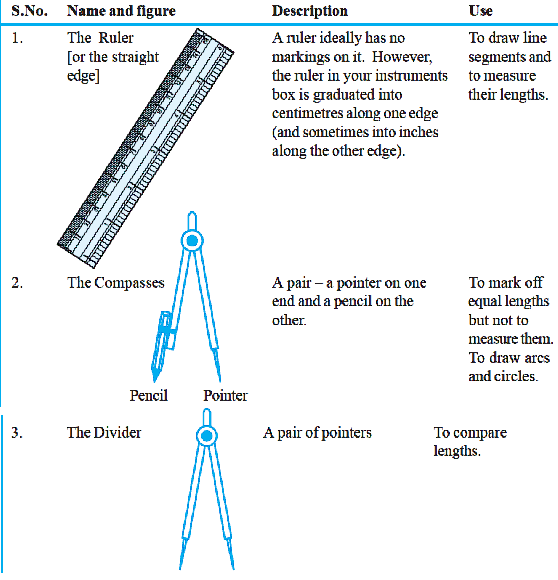
Introduction to geometrical tools

Geometric tools are the instruments used to draw different types of geometric shapes. To draw these shapes, there are different types of tools with different names used while solving problems based on geometry. Different figures have characteristic properties such as length, breadth, diameter, etc. which set them apart from one another and are parameters to produce the figures on paper. Practical geometry or Euclidean geometry is the most pragmatic branch of geometry that deals with the construction of different geometrical figures using geometric instruments such as rulers, compasses, and protractors. 

The early geometer studied figures such as points, lines, and angles that required the use of rulers and compasses only. With the advent of more geometric designs, other geometric tools were invented. Some of the most commonly used geometric tools are:

• Ruler
• Compass
• Protractor
• Divider
• Set-squares

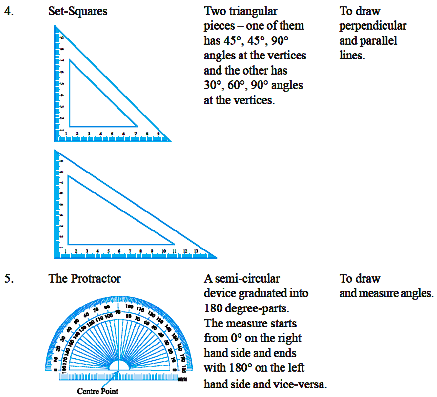
Introduction to circles

Circle is the set of points central from a given point. The distance from that point to the circle is called the radius of the circle .The point from which all the points on a circle are in middle  is known as  the center of the circle.

A circle is named with a single letter, its center

 Construction of a circle,

The circle above has its center at point C and a radius of length r. By definition, all radii of a circle are congruent, since all the points on a circle are the same distance from the center, and the radii of a circle have one endpoint on the circle and one at the center.

All circles have a diameter, too. The diameter of a circle is the segment that contains the center and whose endpoints are both on the circle. The length of the diameter is twice that of the radius. Therefore, all diameters of a circle are congruent, too.

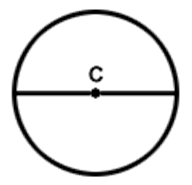
Introduction to line segments

This is a line! It has no endpoints and extends endlessly in both directions.

If you mark two points A and B on it and pick this segment separately, it becomes a line segment

This line segment has two endpoints A and B whose length is fixed. The length of this line segment is the distance between its endpoints A and B.
So, a line segment is a piece or part of a line having two endpoints. Unlike a line, a line segment has a definite length. 

The length of a line segment can be measured either in metric units such as millimetres, centimetres, or customary units like feet or inches. 

Copying an existing line segment

The key to copying a given line segment is to open your compass to the length of the segment; then, using that amount of opening, you can mark off another segment of the same length.

Step 1: Place one end of the compass on one end of the line segment and the other end of the compass on the other end of the line segment.

In the figure given above, AB¯¯¯¯¯¯ is being copied using a compass.

Step 2: Now draw a new line on the sheet of paper.

Step 3: By keeping the measurement obtained using the compass intact, place the pointy end of the compass anywhere on the line and draw an arc over the line using the pencil end.

Step 4: The point on the line where the pointy end was placed becomes one end of the line segment, while the point where the arc and the line meets becomes the other end of the line segment.

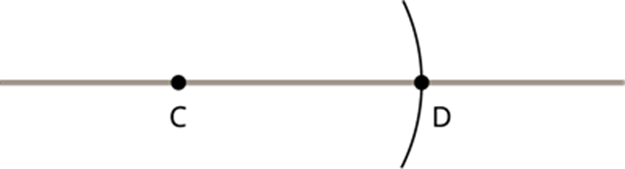
Using the same measurement of AB¯¯¯¯¯¯, CD¯¯¯¯¯¯ is formed.

In other words, AB¯¯¯¯¯¯=CD¯¯¯¯¯¯

If the arc does not fall over the line segment, keep extending the line until it meets the arc at some point.

Introduction to perpendiculars to a line segment

When line segment AB¯¯¯¯¯¯ meets CD¯¯¯¯¯¯ at right angles, then the line segments AB¯¯¯¯¯¯ and CD¯¯¯¯¯¯ are said to be perpendicular.

When two line segments meet at right angles to each other, then the two line segments are said to be perpendicular to each other.

Perpendicular to a line without a point on it,

A perpendicular to a line can also be drawn without a point on it.

Let us look at how to do that.

Construction using rulers and set squares

Step 1: Draw a line using a ruler on the sheet of paper.

Step 2: Place a point P anywhere on the sheet.

Step 3: Place the set square on the line such that the arm having 90^∘  lies on the line.

Step 4: Place a ruler on the other side of the set square.

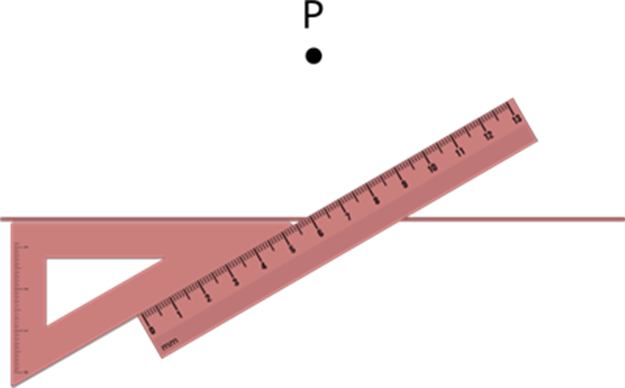
tep 5: While holding the ruler firmly, slide the set square until the other arm of the set square touches the point P.

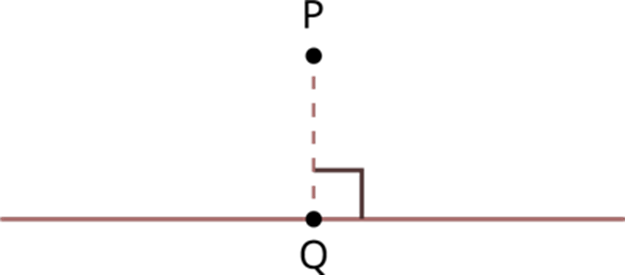
Step 6: Now draw a line from P until it meets the line already drawn at Q.

Construct a perpendicular bisector

Bisecting means dividing a line segment into two equal parts.

 Perpendicular bisector:

When a line segment is divided into two halves by a perpendicular line segment, then the perpendicular line segment becomes the perpendicular bisector.

In the figure given above, CD¯¯¯¯¯¯¯ is the perpendicular bisector of AB¯¯¯¯¯¯

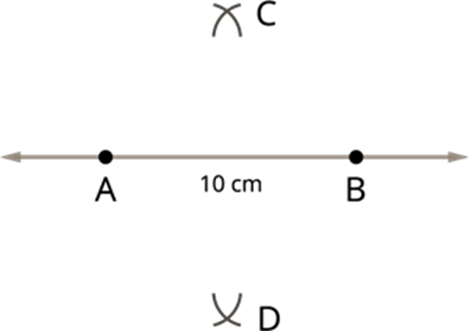
Make a note of the following steps to construct a perpendicular bisector of the line segment AB=10cm.

Step 1: Draw a line and mark two points A and B on it. That is, AB=10cm.

Step 2: Make A as centre and radius more than half of the length of AB, draw two arcs of same length, one above AB and one below AB.

Step 3: Now take B as centre, draw two arcs with the same radius to cut the arcs drawn in step 2. Mark the points of intersection of the arcs as C and D.

Step 4: Then, join C and D. The line CD will intersect AB. Mark the point of intersection as O. CD is the required perpendicular bisector of AB. Now measure the distance between A and O and O and B. We have AO=OB =5cm.

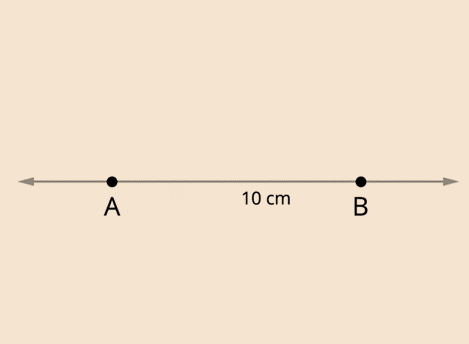
Thus, we have constructed the perpendicular bisector of AB and this perpendicular bisector divides the line AB=10cm into two parts, such that AO =OB =5cm.

 Introduction to angles,

Angle:

When two lines meet, they always meet at a certain angle. An angle is specified using a number followed by a (∘) symbol like 15∘, 120∘, 180∘, and so on.

Example:

In the figure given above, CD¯¯¯¯¯¯¯ meets CB¯¯¯¯¯¯ at 90∘

An angle can be constructed by using a protractor.

Let us see how to construct a an using a protractor.

Step 1: Draw a line segment PA.

Step 2: Place the protractor on the line segment PA by taking the midpoint of the protractor at point P, as shown in the figure.

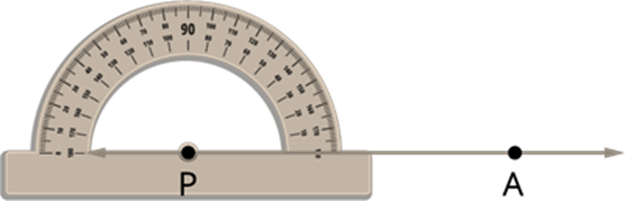
Step 3: On PA from the right, start counting from 0° in the ascending order (counter-clockwise direction and finally mark a point Q using a sharp pencil at the point showing 60° on the semi-circular edge of the protractor.

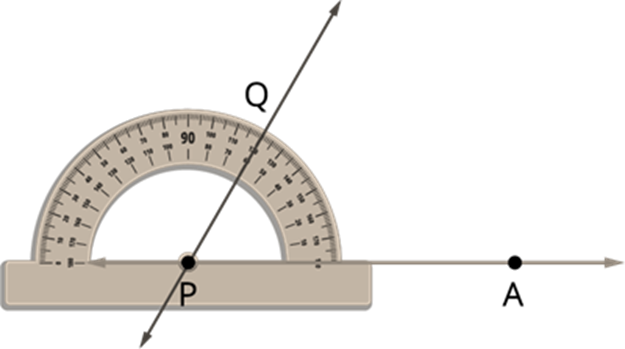
Step 4: Remove the protractor and join PQ.

We get the required angle, ∠APQ= 60°.

Copying an angle

Angles of unknown measurements can be copied using compasses.

Let us see how to copy an angle of unknown measure.

Copying an angle of unknown measure

Step 1: Draw a line on an empty sheet of paper.

Step 2: Consider the already existing angle formed by joining two different lines.

Step 3: With A as centre, draw an arc such that the arc cuts both the lines at B and C.

Step 4: Keeping the measurements of the arc drawn intact, place a point P on the line and with P as centre construct an arc such that the arc meets the line at Q.

Step 5: Similarly, after measuring the distance between B and C using a compass, with Q as centre place the point R on the arc.

Step 6: Join the points P and R to form the copied angle.

Angle bisector of an angle

The angle bisector is formed when a line or line segment divides an angle into two equal parts.

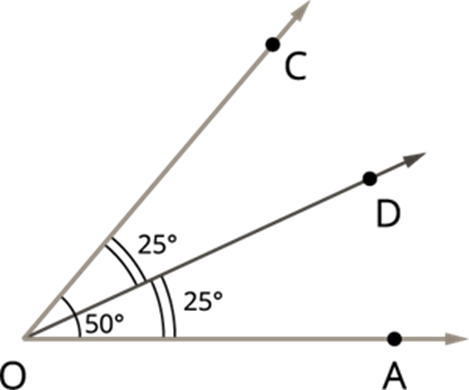
Follow the below steps, construct the bisector of the ∠A with the measure 60°.

 Step 1: Draw the given angle ∠A with the measure 60° using the protractor.

Step 2: Taking A as centre and convenient radius, draw an arc to cut the two lines such that the arc meets the lines at B and C.

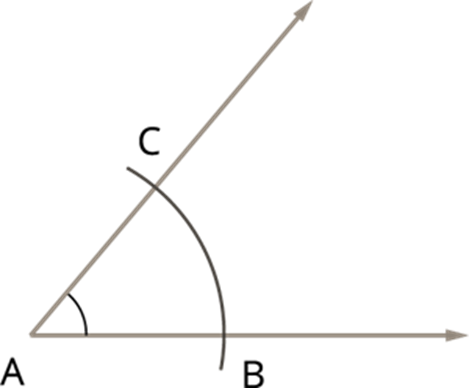
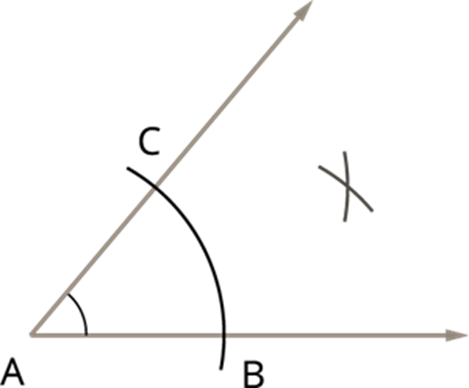
Step 3: With the same radius and B as centre, draw an arc, and with C as centre and with the same radius, cut the already drawn arc.

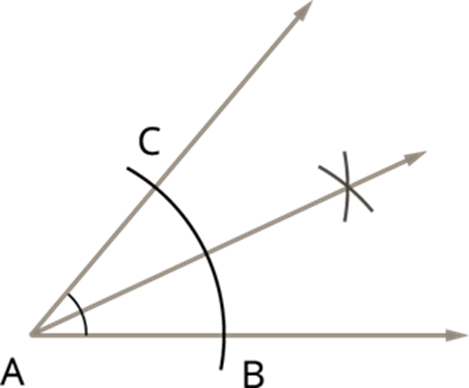
Step 4: Join A and the point of intersection of the arcs to form the angle bisector.

Construction of special angles

i) Construction of 60° angle:

Step 1: First draw a straight line, and mark a point A on it.

Step 2: Take the point A as centre, draw an arc of convenient radius to the line to meet at a point B.

Step 3: With the same radius, take B as centre, draw an arc to cut the previous arc at C.

Step 4: Join AC. Then ∠BAC is the required angle with the measure 60°.

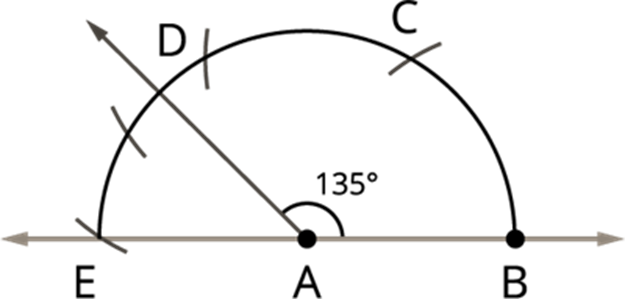
ii) Construction of 135° angle:

Step 1: First draw a straight line, and mark a point A on it.

Step 2: Take the point A as centre, draw an arc as below which meet at a point B.

Step 3: Take radius, and draw an arc for 60°, as shown above. This cuts an arc at point C.

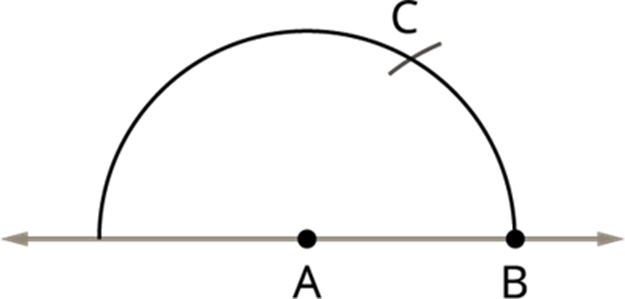
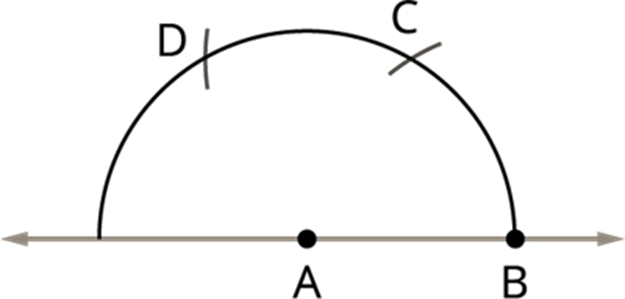
Step 4: Now take C as centre, draw an arc to with the same radius, point it as D. Here the point D gives the angles of 120°.

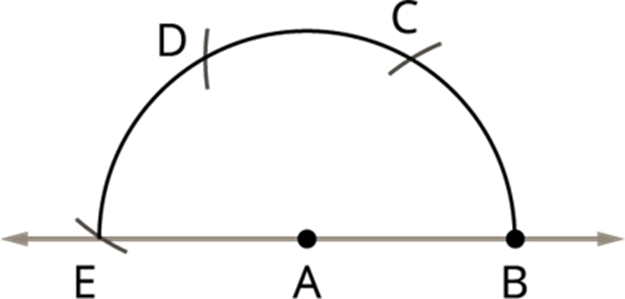
Step 5: With the same radius, draw an arc from the point D that cuts the E which gives the 180°.

Step 6: Finally, draw the angle bisector between the two points D (120°) and E (180°). The angle bisector separates the two points D and E and gives the angle 150°.

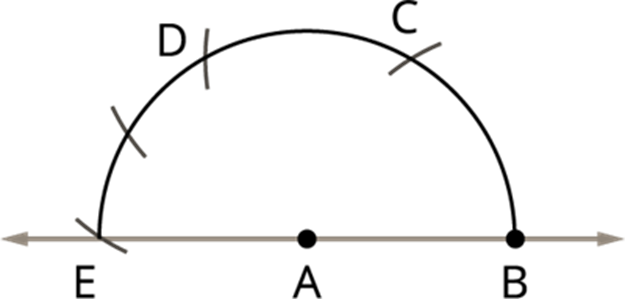
Step 7: Now again find the angle bisector between 150° and 120°, the resultant gives the required angle 135°.

Construction of a circle when its radius is known
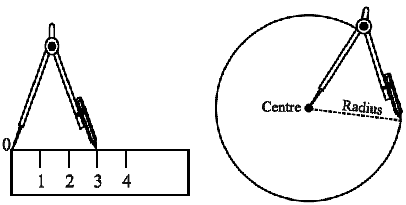
Suppose we want to draw a circle of radius 3 cm. We need to use our compasses. Here are the steps to follow.                             
Step 1   Open the compasses for the required radius of 3 cm.
Step 2   Mark a point with a sharp pencil where we want the centre of the circle to be. Name it as O.
Step 3   Place the pointer of the compasses on O.
Step 4  Turn the compasses slowly to draw the circle. Be careful to complete the movement around in one instant.

 

Line Segment
A line segment is bounded by two end-points. This makes it possible to measure its length with a ruler. 
If we know the length of a line segment, it becomes possible to represent it by a diagram. 

Construction of a line segment of a given length 
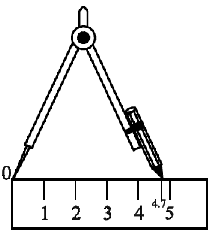
Suppose we want to draw a line segment of length 4.7 cm. We can use our ruler and mark two points A and B which are 4.7 cm apart. Join A and B and get AB . While marking the points A and B, we should look straight down at the measuring device. Otherwise we will get an incorrect value.
Step 1     Draw a line l. Mark a point A on a line l.

Step 2     Place the compasses pointer on the zero mark of the ruler. Open it to place the pencil point upto the 4.7cm mark.

Step 3     Taking caution that the opening of the compasses has not changed, place the pointer on A and swing an arc to cut l at B.

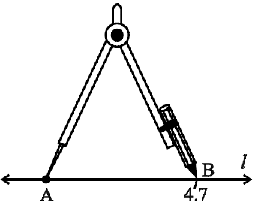
Step 4   AB   is a line segment of required length. 

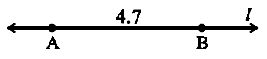
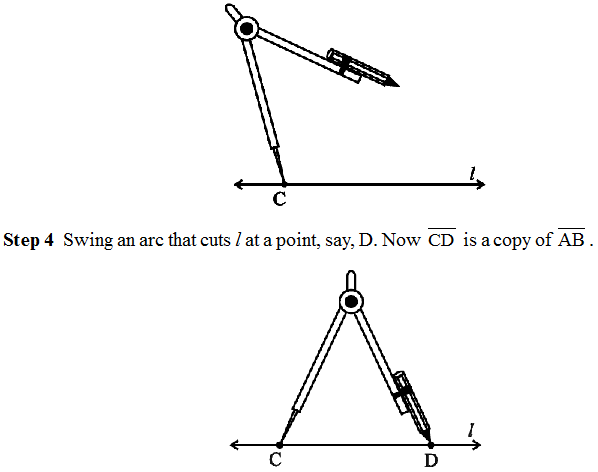
Constructing a copy of a given line segment

 

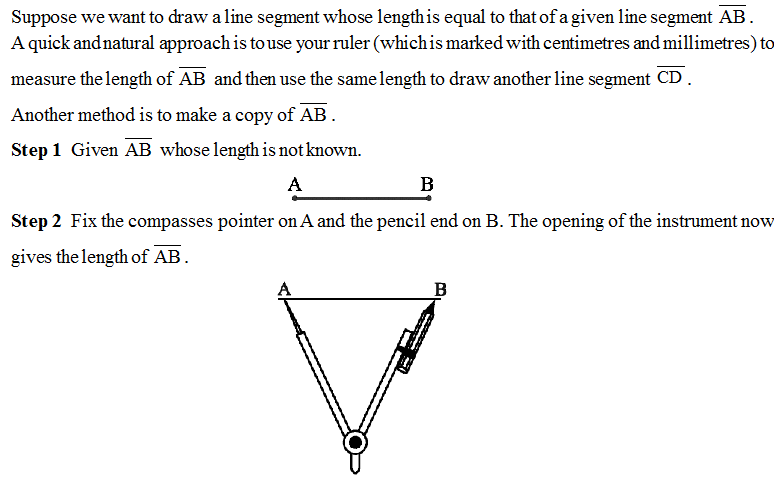
Step 3     Draw any line l. Choose a point C on l. Without changing the compasses setting, place the pointer on C.

Perpendiculars
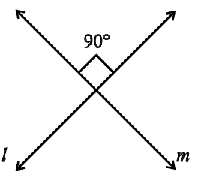
We know that two lines (or rays or segments) are said to be perpendicular if they intersect such that the angles formed between them are right angles.
In the figure, the lines l and m are perpendicular.

Perpendicular to a line through a point on it
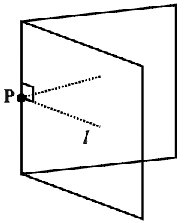
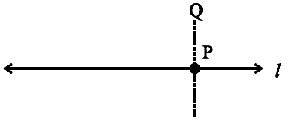
Let us do an activity. Given a line l drawn on a paper sheet and a point P lying on the line. It is easy to have a perpendicular to l through P.
We can simply fold the paper such that the lines on both sides of the fold overlap each other.
Tracing paper or any transparent paper could be better for this activity. Let us take such a paper and draw any line l on it. Let us mark a point P anywhere on l.  
Fold the sheet such that l is reflected on itself; adjust the fold so that the crease passes through the marked point P. Open out; the crease is perpendicular to l.

Construction perpendicular 
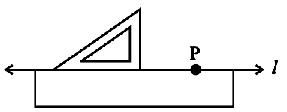
Method-1 (Using Ruler and A Set-square)
Step 1     A line l and a point P are given. Note that P is on the line l.

Step 2     Place a ruler with one of its edges along l. Hold this firmly.

Step 3     Place a set-square with one of its edges along the already aligned edge of the ruler such that the right angled corner is in contact with the ruler.

Step 4     Slide the set-square along the edge of ruler until its right angled corner coincides with P.

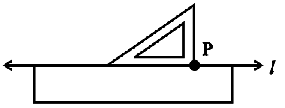
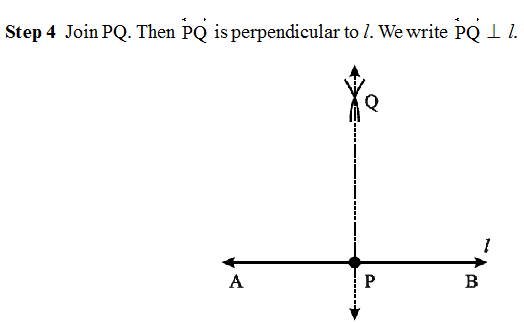
Step 5    Hold the set-square firmly in this position. Draw PQ along the edge of the set-square.

PQ is perpendicular to l.

Method-2 (Using to Ruler and Compasses)
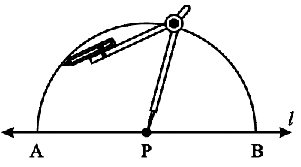
Step 1     Given a point P on a line l.

Step 2    With P as centre and a convenient radius, construct an arc intersecting the line l at two points A and B.

Step 3    With A and B as centres and a radius greater than AP construct two arcs, which cut each other at Q.

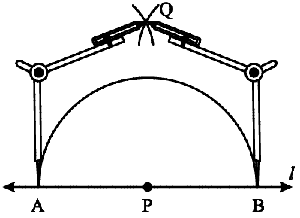
Construction Perpendicular to a line through a point not on it
Method-1 (Using Ruler and A Set-square)
Step 1     Let l be the given line and P be a point outside l.

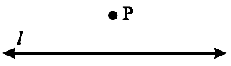
Step 2     Place a set-square on l such that one arm of its right angle aligns along l.

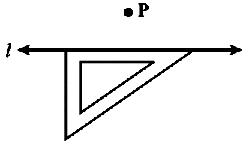
Step 3     Place a ruler along the edge opposite to the right angle of the set-square.

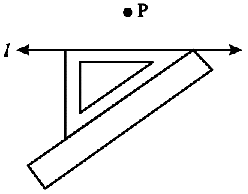
Step 4     Hold the ruler fixed. Slide the set-square along the ruler till the point P touches the other arm of the set-square.

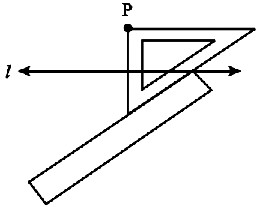
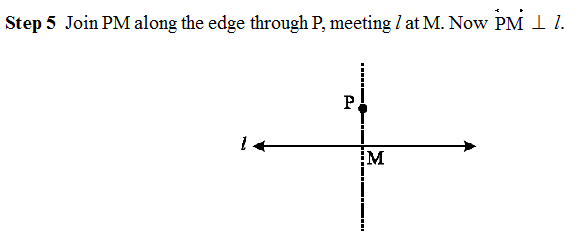
Method-2 (Using Ruler and Compasses)
This is the more convenient and accurate method.
Step 1     Given a line l and a point P not on it.

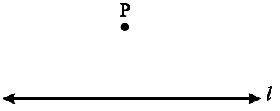
Step 2    With P as centre, draw an arc which intersects line l at two points A and B.

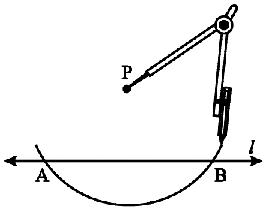
Step 3     Using the same radius and with A and B as centres, construct two arcs that intersect at a point, say Q, on the other side.

 

 

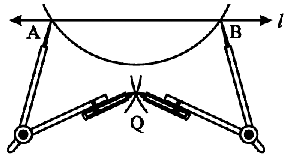
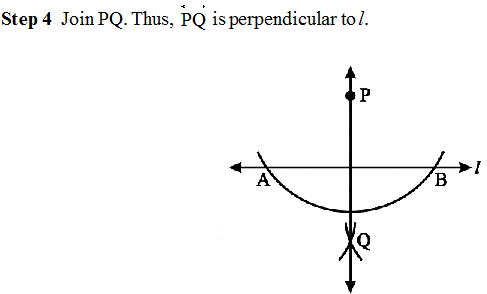
The perpendicular bisector of a line segment

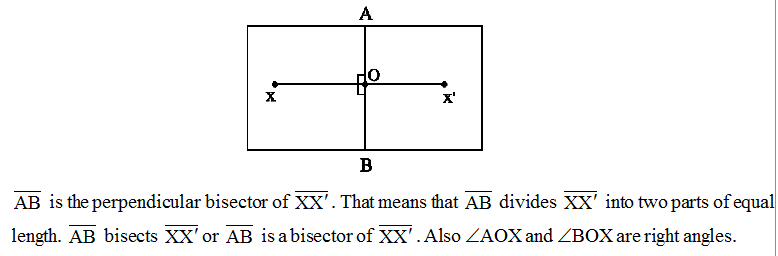
Construction using ruler and compasses

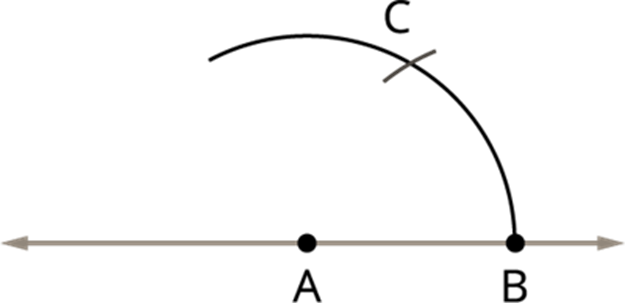
Step 1     Draw a line segment AB  of any length.

Step 2    With A as centre, using compasses, draw a circle. The radius of your circle should be more than half the length of AB.

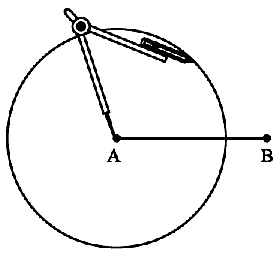
Step 3    With the same radius and with B as centre, draw another circle using compasses. Let it cut the previous circle at C and D.

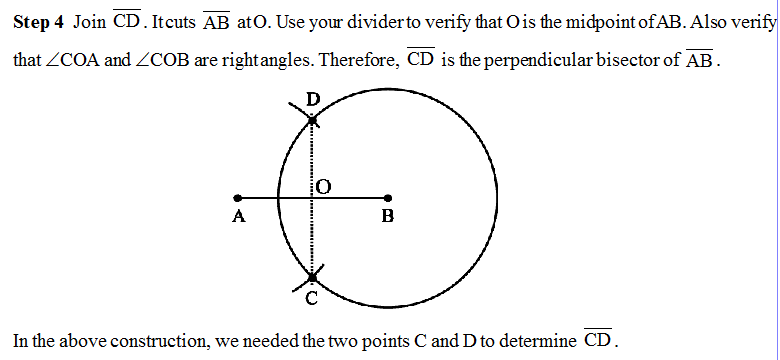
Angles
Constructing an angle of a given measure
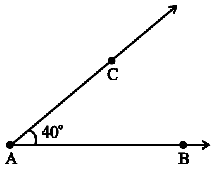
Suppose we want an angle of measure 40°. 
Here are the steps to follow :

Step 1     Draw AB of any length.

Step 2     Place the centre of the protractor at A and the zero edge along AB.

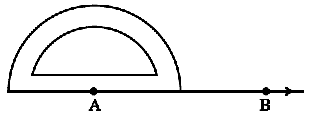
Step 3     Start with zero near B. Mark point C at 40°.

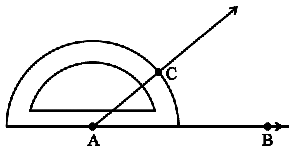
Step 4     Join AC. ∠BAC is the required angle.

Bisector of an angle
Construction with ruler and compasses
Let an angle, say, ∠A be given.

Step 1     With A as centre and using compasses, draw an arc that cuts both rays of ∠A . Label the points of intersection as B and C.

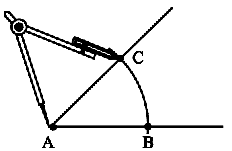
Step 2    With B as centre, draw (in the interior of ∠A ) an arc whose radius is more than half the length BC.

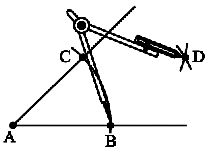
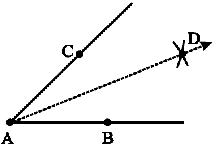
Step 3    With the same radius and with C as centre, draw another arc in the interior of ∠A. Let the two arcs intersect at D. Then AD  is the required bisector of∠A .    

 

Construction of Special Angles 
Constructing a 60° angle
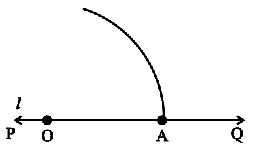
Step 1     Draw a line l and mark a point O on it.

Step 2     Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line  PQ at a point say, A.

Step 3    With the pointer at A (as centre), now draw an arc that passes through O.

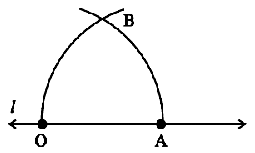
Step 4     Let the two arcs intersect at B. Join OB. We get ∠BOA whose measure is 60°.

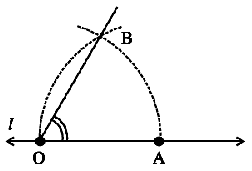
Constructing a 30° angle
Construct an angle of 60° as shown earlier. Now, bisect this angle. Each angle is 30°, verify by using a protractor.

Constructing a 120° angle
 An angle of 120° is nothing but twice of an angle of 60°. Therefore, it can be constructed as follows :
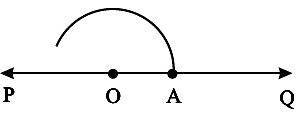
 Step 1     Draw any line PQ and take a point O on it.

Step 2    Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line at A.

Step 3    Without disturbing the radius on the compasses, draw an arc with A as centre which cuts the first arc at B.

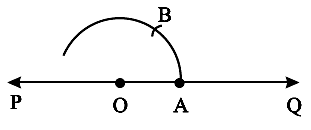
Step 4     Again without disturbing the radius on the compasses and with B as centre, draw an arc which cuts the first arc at C.

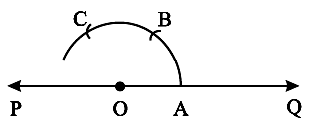
Step 5     Join OC, ∠COA is the required angle whose measure is 120°.

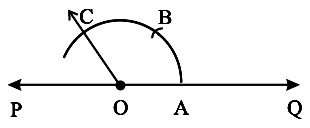
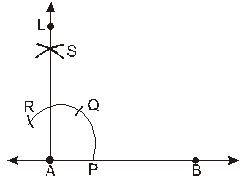
Constructing a 90° angle
Step 1    With A as centre and any suitable radius draw an arc cutting AB at P. 
Step 2    With P as centre and the same radius as before cut the arc of Step 1 at Q. With Q as centre and the same radius cut the arc again at R.     
Step 3    With Q and R as centres and any convenient radius (same for both) draw arcs cutting at S. Join A to S and produce A to L. Then ∠BAL = 90°, i.e., AL is perpendicular to AB at A.