Chapter 6: Integers

Introduction
We have learnt about natural and whole numbers in the previous chapters. But when we subtract a greater whole number from a smaller whole number, then the difference will not be a whole number. Hence, there is a need to extend the number system to include such numbers. Their are many examples in hour day to day life related to such type of numbers.
(i)    During the winter season, the minimum temperature in Shimla may be 5°C below 0°C. 
So we represent this as –5°C, read as minus five degree centigrade.
(ii)     the depth of an ocean, say 300 metres below the mean sea level, can be expressed as –300 metres high. If height is considered as positive, depth is considered as negative height and vice versa. 

Integers
Their are infinite numbers with negative sign on the numebr line. All these numbers are less than zero and are called negative numbers. They are –1, –2, –3.  
Whole numbers along with the negative numbers are called integers.
Their are some important properties with integers.
(i)    There are infinite positive numbers to the right of zero and there are infinite negative numbers to the left of zero as well.
(ii)    In the number line of integers, every number on the right is greater than all the numbers on its left.
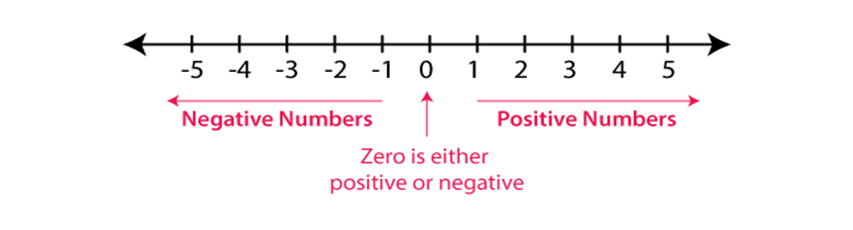
(iii)    Zero is neither negative nor positive.
The natural numbers 1, 2, 3, ... , etc., in the system of integers are called positive integers. The numbers to the left of zero are called negative integers and are always denoted as –1, –2, –3, ... , etc. . The whole number 0 is neither a positive integer nor a negative integer.

Chapter - 6

Integers

Introduction to integers

Introduction

The numbers 1, 2, 3, 4, 5 are Natural numbers and so on. When zero is added in to the collection of natural numbers, we get the new numbers called as whole numbers, that is, 0, 1, 2, 3, and 4 and so on.

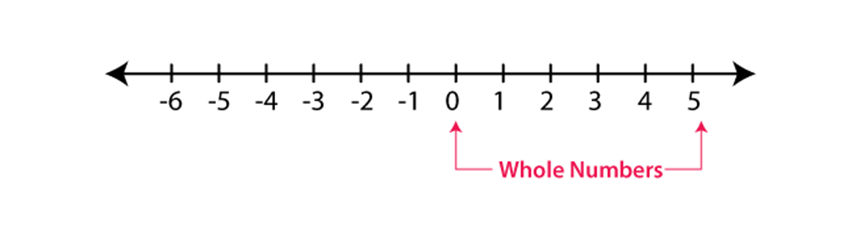
 There are negative numbers also that exist. When the whole numbers and the negative numbers are arranged together, the resultant of numbers will look as shown ….-4,-3,-2,-1, 0, 1,2,3,4 and so on. This resultant numbers are called as an Integer.

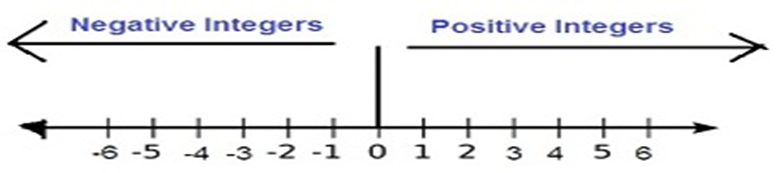
 Numbers that are more than zero - 1, 2, 3... Are called positive integers and numbers that are below zero – 1, – 2, – 3 ... are called negative integers.

 Representing integers on a number line

The integers are represented on the number line as follows:

The numbers that are the left of number zero are negative integers while numbers to the right of number zero are positive integers.

 Comparing integers

If we are at the zero mark on the number line, then either we can go negative integers left towards or positive integers right towards.
When moving left towards zero on the number line, the value of positive integer’s decreases and negative are increasing. When we move right direction from zero on the number line, the value of negative integers decreases.
Two integers that are middle from zero and on opposite sides of zero are called opposite numbers. The total of an integer and its opposite is zero altogether.

9 > 5 (since 9 is to the right of 5)
4 > 0 (since 4 is to the right of 0)
-7 < -2 (since -7 is to the left of -2)
-6 < 7 (since -6 is to the left of 7)

1. A positive number is greater than always than the negative number.

2.  When two positive integers are compared, then the integer with more number of digits is always greater than the integer with less number of digits.    (ii) If two positive integers have the exactly same number of digits, then compare the left-most digit of two numbers till reaches across unequal digits.

3. When compared with two negative integers, the greatest number with a negative sign is the smaller of two negative integers.

4. Negative numbers are less than zero always.

5. Positive numbers are greater than zero always.

Ordering integers

Order of integers: When we go to the right the integer’s value will increase. Therefore number 5 is greater than integer 3, integer 3 is greater than 2 and number 0 is greater than -2, -2 is greater than integer 2 and so on.

We can say that the number, – 4 < – 3, – 3 < – 1, – 2 < 0, 0 < 2, 2 < 3, 3 < 4 so on.

The number line tells us that which integers are lie between two integers and which integer is the greater integer. The number line shows how much steps should be taken to move forward or backward in order to go from one integer to another.

 Addition of integers

Addition of Integers
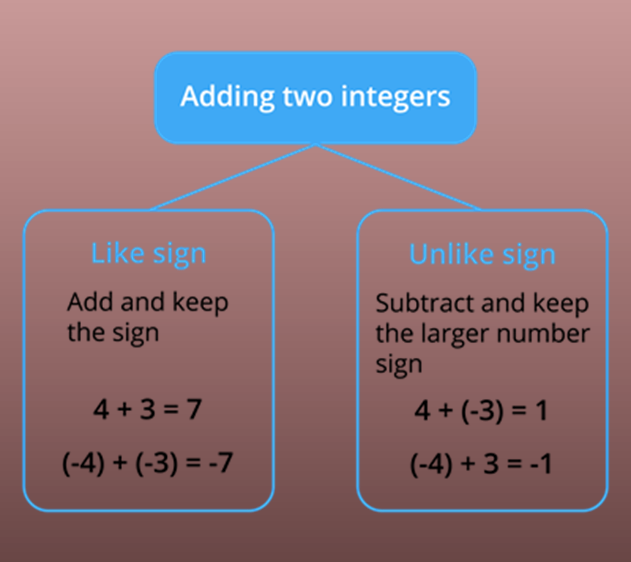
Adding integers without using number line
When the integers to be added with the same sign, add the numbers and assign the same sign to the sum
Sum of positive integers is a positive integer
Sum of negative integers is a negative integer

 

Additive Inverse

When two integers are added to each other, and their sum is zero, it means these two integers are called additive inverse of each other.
For example, -2 is the additive inverse of 2

 

Addition of integers on a number line,

Addition of Integers

The sums of any two positive numbers are also known as the addition of two positive integers. For e.g. 4+3= 7.

The sum of any two negative integers exactly same as positive integer addition except that the difference that answer will come with a negative sign. For e.g. (–4) + (–3) = (4+3) = –7

Whenever we have two integers, one positive and one negative integer, the integer must get subtracted, and the answer will use the sign of the integer whichever is bigger than second integer.

Ignore the signs of the numbers when you want to choose a bigger integer.

For e.g.

(3) + (-1) = 3-1 = 1.   3> 1. Hence the answer is positive.

(2) + (-4) = 2-4 = -2.   4>2. Hence the answer is negative.

Numbers such as 1 and – 1, 5 and – 5, when added always give their sum as zero. They are known as the additive inverse of each other.              

We can perform Operations of addition and subtraction by using a number line.

We move forward to the right, whenever we want to add a positive number   we move backward to the left, whenever we want to add a negative number

Whenever we want to subtract a positive number, we move backward to the left.

We move forward to the right, whenever a negative number is subtracted,

Addition of Integers on a Number Line

Addition of Two Positive Integers

Example

Add integer 3 and integer 4 on the number line.

Solution

To add numbers 3 and 4, first, we move 3 steps forward to the right of zero then again move 4 steps forward to the right from point 3.

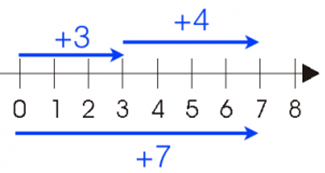
We then reached to the point 7, therefore numbers (+3) + (+4) = number +7

This tells that the sum of any two positive integers is always get positive number

Addition of Two Negative Integers

Example

Add numbers (-2) and (-5) using a number line.

Solution

To add numbers (-2) and (-5), first move 2 steps  backward to the left of zero then again move 5 steps backward  to the left of (-2). 

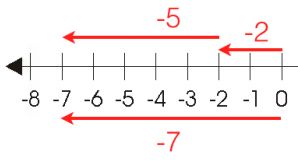
Then we will be reached to the point (-7), therefore integer (-2) + (-5) = -number 7.

This tells us that the sum of any two negative integers is always get the negative number

Addition of One Negative and One Positive Integer

A. when a positive number is greater than the negative number

To add  number (+6) and number  (-2),

first move forward 6 steps to the right from zero

Then move 2 steps backward to the left of point 6.

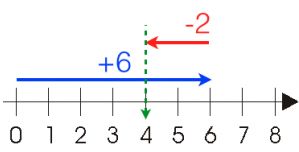
 Then we get the point 4, hence number (+6) + (-2) = number +4

b. When a negative integer is greater than the positive integer

2. To add Number (-5) and number (+4),

first  move 5 steps backward  to the left of zero

Then move 4 steps forward to the right from point (-5).

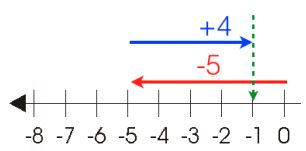
Then we get the point -1, hence number (-5) + (+4) = number (-1)

C. Additive Inverse

If we add numbers like (-2) and 2 then we get the result as zero. So these are called the Additive inverse of each other.

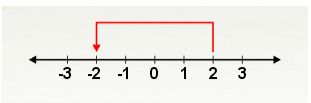
First move backward 2 steps to the left of zero

Then move forward two steps to the right of (-2).

Then finally reached to zero.

Therefore, when positive number and negative number of the same integer are added then the answer will be the zero.

Subtraction of integers,

Subtraction of Two Positive Integers

Example

Subtract number 2 from number 5.

Solution

To subtract number 2 from number 5,

first, move 5 steps forward  to the right from zero then

Move 2 steps backward to the left

Then we are at the point 3, so the number 5 – (+2) = 5 – 2 = 3

Subtracting an integer from another is somewhat similar as performing addition of integer’s additive inverse.
Additive inverse for an integer X, is –X.
Example: Subtract number 4 from -3
4 – (-3) = 4 + 3 = 7 (the additive inverse of number -3 is 3.)

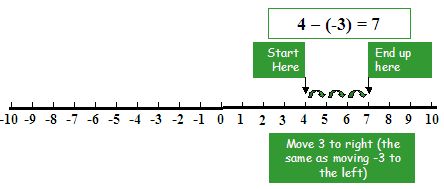
The sum of all positive and negative numbers always keeps the sign of a larger number

 Subtraction of integers on a number line

Subtraction of a number means to add its opposite numbers.

 Subtracting integers on number line

Positive integer is Subtracting from a positive integer, e.g.  9 – 3 then 9 – 3 = 6
Negative integer is Subtracting from a positive integer, e.g.  8 – (-6) then 8 – (-6) = 14
A positive integer is Subtracting from a negative integer, e.g. -7 – 6 then (-7) – 6 = -13
Subtracting a negative integer from a negative integer, say  e.g. -5 – (-7)-5 – (-7) = 2

Subtraction of One Negative number and One Positive number

To subtract a positive integer from any other integer.

Example 

Subtract number 3 from number (-4)

Solution

To subtract number (-4) from number (3),

first, we have to move backward  4 steps to the left of zero

Then move 3 steps forward more to the left.

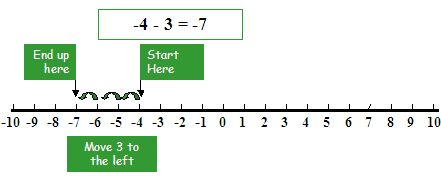
Then reached to point (-7), therefore point (-4) – (+3) = point (-4) + (-3) = number -7.

 To subtract a negative number from any other number

Example  Subtract number (-3) from number (4)

Solution

To subtract number  (-3) from number (4), first move 4 steps forward to the right of zero then move 3 steps forward more to the right.

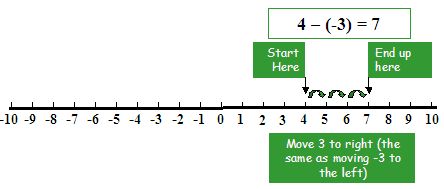
When we get point (7),  

Number (4) – (-3) = number (4) + (+3) = number +7

 

 Subtraction of One Negative number and One Positive number

To subtract a positive number from any other number.

Example

Subtract number 3 from number (-4)

Solution

To subtract number (-4) from number (3),

first, move 4 steps backward  to the left of zero

Then move 3 steps backward more to the left.

As we get point  (-7),

Therefore number (-4) – (+3) = number (-4) + (-3) = number -7.

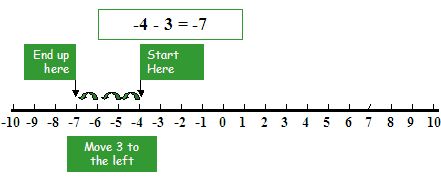
Subtracting integers on number line

1. from a positive integer Subtracting a positive integer  then  5 – 2
5– 2 = 3
2. From a positive integer, Subtracting a negative integer e.g. 6 – (-5)
6– (-5) = 11
3. From a negative integer, subtracting a positive integer then -5 – 9
(-5) – 9 = -14
4. From a negative integer, Subtracting a negative integer then -6 – (-8)
-6 – (-8) = 2
5. We move to the backward in left, whenever we want to subtract a positive integer,
6. Whenever a negative integer is subtracted, we move forward to the right the reason behind is that we are having a bigger integer.  E.g. 6- (-4) = 6+4 = 10.
7. Add the additive inverse of the integer that is being subtracted, whenever we want to subtract a number from another number to the other number.
E.g. In the case of 7 - (-3), the additive inverse of -3 can be used. The additive inverse of -3 is 3.

Representation of integers on a number line

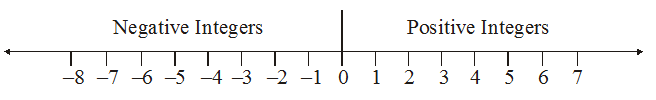
First we draw a line and mark some points at equal distance on it as shown in the figure. Mark a point as zero on it. Points to the right of zero are positive integers and are marked + 1, + 2, + 3, etc. or simply 1, 2, 3 etc. Points to the left of zero are negative integers and are marked – 1, – 2, – 3 etc. 
In order to mark – 6 on this line, we move 6 points to the left of zero.

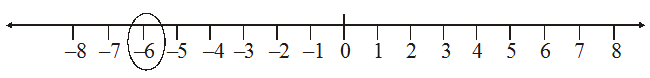
In order to mark + 2 on the number line, we move 2 points to the right of zero.

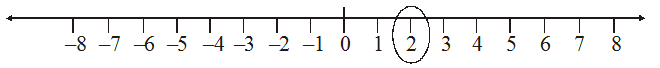
Ordering of integers
Let we observe the integers which are represented on the number line.

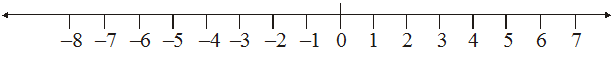
We know that 7 > 4 and from the number line shown above, we observe that 7 is to the right of 4. 
Similarly, 4 > 0 and 4 is to the right of 0. Now, since 0 is to the right of –3 so, 0 > – 3. Again, – 3 is to the right of – 8 so, – 3 > – 8.
Thus, we see that on a number line the number increases as we move to the right and decreases as we move to the left.
Therefore, – 3 < – 2, – 2 < – 1, – 1 < 0, 0 < 1, 1 < 2, 2 < 3 so on. 
Hence, the collection of integers can be written as..., –5, –4, – 3, – 2, – 1, 0, 1, 2, 3, 4, 5...

Ex.    Write all integers between 
         (i) – 2 and 3         (ii) – 4 and 2

(i)     The integers between – 2 and 3 are –1, 0, 1, 2.
(ii)     The integers between – 4 and 2 are – 3, – 2, –1, 0, 1.

Operation on Integers
Addition : In integers, addition can perform using following rule. 
(i)     When adding integers with like signs (both positive or both negative), add their absolute values, and place the common sign before the sum. 
(ii)     When adding integers of unlike signs, find the difference of their absolute values, and give the result the sign of the integer with the larger absolute value. 
(iii)    When the addition and subtraction signs are placed side by side without any number in between, these two opposite signs give a negative sign. 
Subtraction : Subtraction is reverse operation of addition.

Ex.1    Consider 8 – 5. Actually we have to subtract + 3 from 8. So, we need to find a number which when added to 3 gives 8. 
sol:     The answer 5, i.e., 8 – 3 = 8 + (– 3) = 5 
We can change subtraction to addition by adding the additive inverse of the second number to the first number. In the above example –3 is the additive inverse of +3 and vice versa is also possible.
Ex.2     Find the sum of (– 9) + (+ 4) + (– 6) + (+ 3)
Sol.     We can rearrange the numbers so that the positive integers and the negative integers are grouped together. We have 
(– 9) + (+ 4) + (– 6) + (+ 3) = (– 9) + (– 6) + (+ 4) + (+ 3) = (– 15) + (+ 7) = – 8

Ex.3     Find the value of (30) + (– 23) + (– 63) + (+ 55)
Sol.    (30) + (+ 55) + (– 23) + (– 63) = 85 + (– 86) = – 1 

Ex.4      Subtract (– 4) from (– 10)
Sol.:     (– 10) – (– 4) = (– 10) + (additive inverse of – 4) = –10 + 4 = – 6    

 Ex.5     Subtract (+ 3) from (– 3)
 Sol.:     (– 3) – (+ 3) = (– 3) + (additive inverse of + 3)     = (– 3) + (– 3) = – 6

 

Addition of integers on a number line
(i)     Let us add 3 and 5 on number line.

On the number line, we first move 3 steps to the right from 0 reaching 3, then we move 5 steps to the right of 3 and reach 8. Thus, we get 3 + 5 = 8

(ii)     Let us add – 3 and – 5 on the number line.

On the number line, we first move 3 steps to the left of 0 reaching – 3, then we move 5 steps to the left of – 3 and reach – 8. 
Thus, (– 3) + (– 5) = – 8.
We observe that when we add two positive integers, their sum is a positive integer. When we add two negative integers, their sum is a negative integer. 

(iii)     Suppose we wish to find the sum of (+ 5) and (– 3) on the number line. First we move to the right of 0 by 5 steps reaching 5. Then we move 3 steps to the left of 5 reaching 2.

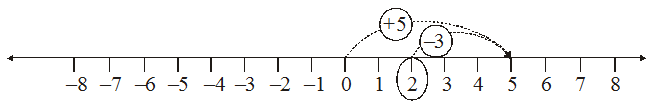
Thus, (+ 5) + (– 3) = 2
(iv)     Similarly, let us find the sum of (– 5) and (+ 3) on the number line. First we move 5 steps to 
the left of 0 reaching – 5 and then from this point we move 3 steps to the right. We reach the point – 2. 
Thus, (– 5) + (+3) = – 2.    

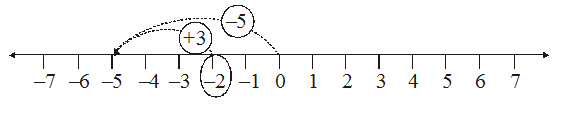
Subtraction of Integers with the help of a Number Line
We have added positive integers on a number line. For example, consider 6+2. We start from 6 and go 2 steps to the right side. We reach at 8. So, 6 + 2 = 8. 

We also saw that to add 6 and (–2) on a number line we can start from 6 and then move 2 steps to the left of 6. We reach at 4. So, we have, 6 + (–2) = 4.

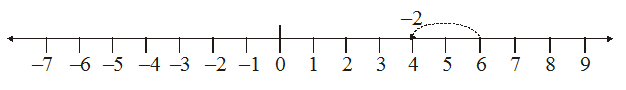
Thus, we find that, to add a positive integer we move towards the right on a number line and for adding a negative integer we move towards left. We have also seen that while using a number line for whole numbers, for subtracting 2 from 6, we would move towards left.

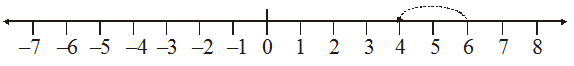
i.e. 6 – 2 = 4

Ex.1     Find the value of – 8 – (–10) using number line
Sol.:    – 8 – (– 10) is equal to – 8 + 10 as additive inverse of –10 is 10. 
On the number line, from – 8 we will move 10 steps towards right. 

We reach at 2. Thus, –8 – (–10) = 2
Hence, to subtract an integer from another integer it is enough to add the additive inverse of the integer that is being subtracted, to the other integer.

Ex.2 Subtract the sum of 998 and – 486 from the sum of – 290 and 732.
Sol. Sum of 998 and – 486 is 998 + (– 486) = (998 – 486) = 512
Sum of – 290 and 732 is  – 290 + 732  = 732 – 290 = 442
Now, 442 – 512 = 442 +(–512) = – 70
[We subtract 442 from 512 and give minus sign to  the result]

Ex.3  On a particular day, the temperature at Dehradun at 10 AM was 20ºC but by midnight , it fell down to 11ºC. The temperature at Bangaluru at 10AM the same day was 30º C but fell down to 18º C by the midnight . Which fall is greater ?
Sol.    Fall in temperature at Dehradun = 20ºC – 11ºC = 9ºC
Fall in temperature at Bangaluru= 30ºC – 18ºC = 12ºC
∴The fall in temperature at Bangaluru is greater and is 12ºC.