- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Comparing Numbers
Take two numbers. The number with greater number of digits is greater. However, if the two numbers have the same number of digits, then the number which has a larger left most digits is larger. If this digit also happens to be the same, then we proceed to next digit and use the same criterion and so on.
Ex: Which is greater of 270346 and 48356?
Sol. 270346 has 6 digits
48356 has 5 digits
6 digits are more than 5 digits
∴ 270346 is greater than 48356
or 270346 > 48356
Greater number has more number of digits.
Ex: Find the greatest and the smallest numbers from the following group of numbers :
23787,6895, 24569, 24659
Sol. Greatest number : 24659
Smallest number : 6895.
(i) Making number without repetition of digits : In case of non-repetition of digits, it is better if we start making the number from left.
Ex: Write the greatest and the smallest 5-digit numbers by using each of the digits 8, 4, 7, 0, 2 only once.
Sol. For the greatest number, we write the greatest digit 8 in the T-thousands column. Next smaller digit in the thousands column and so on.
∴ The greatest number = 87420.

For the smallest number, we write the smallest digit in the T-thousands column. But here 0 is the smallest digit. 0 is not written on the extreme left of a number. So, we write 2 in the T-thousands column and 0 in the thousands column. Next digit greater than 2 is written in the hundreds column and so on.
∴ The smallest number = 20478

(ii) Making number with repetition of digits : In case of repetition of digit, it is better if we start making number from right.
Ex: Write the greatest and smallest numbers of 4 digits using all the digits 8,0, 5.
Sol For greatest number, select the smallest digit 0 and write in the ones column. Next greater digit is written in the tens column. Next greater digits 8 is written in the hundreds column. Since no digit greater than 8 given, so we repeat 8 in the thousands column.
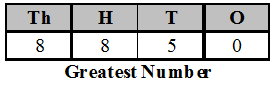
∴ The greatest number = 8850
For smallest number, select the greatest digit 8 and write in the ones column. Next smaller digit in tens column and so on. Repeat the smallest digit in the end. But here 5 is smaller than 8 and then comes 0 which cannot be repeated in the end.
So, we write 5 in the end and repeat 0 in the tens place.
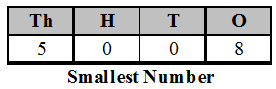
∴ The smallest number = 5008.
ESTIMATION IN NUMBER OPERATION
410 is closer to 400, so it is rounded off to 400, correct to the nearest hundred.
889 lies between 800 and 900.
It is nearer to 900, so it is rounded off as 900 correct to nearest hundred.
Numbers 1 to 49 are closer to 0 than to 100, and so are rounded off to 0.
Numbers 51 to 99 are closer to 100 than to 0, and so are rounded off to 100.
Number 50 is equidistant from 0 and 100 both. It is a common practice to round it off as 100.
(i) Estimating (Rounding) to the Nearest Ten : To round off a number to the nearest ten consider the ones digit. If the ones digit is 5 or greater than 5, then change the ten’s digit to the next higher digit and ones digit to zero. If the ones digit is less than 5, then leave the tens digit unchanged but change the ones digit to zero.
(ii) Estimating (Rounding) to the Nearest Hundred : To round off a number to the nearest hundred, consider the tens digit. If the ten’s digit is 5 or greater than 5, then change the hundreds digit to the next higher digit and tens, ones digits to zeros. If the tens digit is less than 5, then leave the hundreds digit unchanged but change the tens and ones digits to zeros.
(iii) Estimating (Rounding) to the nearest Thousand : To round off a number to the nearest thousand, consider the hundreds digit. If this digit is 5 or greater than 5, then change the thousands digit to the next higher digit and change all the other digits before that to zeros. If the hundreds digit is less than 5, then leave the thousands digit unchanged but change all the other digits before that to zeros.
Ex : Estimate: 5,290 + 17,986.
Sol.: You find 17,986 > 5,290.
Round off to thousands.
17,986 is rounds off to 18,000
+5,290 is rounds off to + 5,000
Estimated sum = 23,000.
Ex : Estimate: 5,673 – 436.
Sol.: 5,673 rounds off to 5,700
– 436 rounds off to – 400
Estimated difference = 5,300.
Ex : Estimate the following products :
(i) 87 × 313 (ii) 9 × 795 (iii) 898 × 785
Sol. (i) 87 is rounded off to 90
313 is rounded off to 300
∴ Estimated product = 90 × 300 = 27000
(ii) 9 is not rounded off [ ∴ it is a one-digit no.
795 is rounded off to 800
∴ Estimated product = 9 × 800 = 7200
(iii) 898 is rounded off to 900
785 is rounded off to 800
∴ Estimated product = 900 × 800 = 720000.
(iv) Estimation in Quotients : In the process of estimation in quotients, we round off the dividend and the divisor before the process of division.
Ex: Estimate the following quotients :
(a) 81 ÷ 17 (b) 7525 ÷ 365
Sol. (a) 81 is rounded to 80
17 is rounded to 20
To get the estimated quotient think of dividing 80 by 20 or 8 by 2.
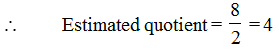
(b) 7525 is rounded to 8000
365 is rounded to 400
To get the estimated quotient think of dividing 80 by 4.
∴ Estimated quotient = 20.
Comparing numbers
Numbers are compared to check which one is higher/smaller than the others. Following things are checked to know that a number is greater or smaller:
If the number of digits in the numbers are different. The number having more digits is greater and the other is smaller.
- For example, among the two numbers 324 and 22, 324 is higher as it has more number of digits. 22 has lower number of digits, hence it is smaller.
- For example, among 221, 34, 1356, 222, 45225, 45225 is the highest and 34 is the lowest.
If the number of digits is equal then the digit at the highestplace is compared.
- If the digits at the highest place are different, the higher value is larger number and the lower value is the smaller number.
- For example, among 235 and 643, the number of digits are same but digit at highest (here hundreds) place, is 2 and 6. Since 6 is higher than 2, hence 643 is higher and 235 is smaller.
- If the digits at the highest place are equal, then the next higher place is compared and so on.
- For example, among 235 and 245, the number of digits and digit at highest place are same so digit at 2nd highest (tens) place is compared. Since 4 is higher than 3, hence 245 is higher and 235 is smaller.
- For example, among 267542, 267894 and 267843, the number of digits and digits at 4 highest places are same (for 2nd and 3rd number) so digit at 5th highest place is compared. Since 9 is higher than 4, hence 267894 is higher than 267843 and 267542.
- Books Name
- MD AFZAL AHMAD Mathematics Book
- Publication
- MD AFZAL AHMAD
- Course
- CBSE Class 6
- Subject
- Mathmatics
Comparing Numbers
How to compare numbers:
We do compare numbers by seeing which number is larger or which one is smaller.
Let we have numbers like 7,1, 3, 9, 5.
By seeing we can say, here 1 is the smallest number and 9 is the largest number.
Examples:
Rules to compare numbers
1. Count the number of digits. Number with more digits is greater.

How many numbers can we make from given number of digitswithout repeatation of digits.
Let we have four digits, like 5, 3, 4, 6. We want to make four different numbers using these digits without any repeatation.
These four numbers are 3,456, 4,356, 5,346 , 6,543
Here, Smallest number is 3,456 and largest number is 6,543.
Arranging Numbers.
Ascending Order:-Arrangement of numbers from smallest to greatest
Example:- 17<19<35<102
Descending Order:-Arrangement of numbers from greatest to smallest
Example:- 102> 35>19>17

 Param Publication
Param Publication
