2. Expressions and Equations

Variable
In the above example, we found a rule to give the number of matchsticks required to make a pattern of Ls. The rule was: Number of matchsticks required = 2n Here, n is the number of Ls in the pattern, and n takes values 1, 2, 3, 4,.... 
Let us look at Table 1 once again. In the table, the value of n goes on changing (increasing). As a result, the number of matchsticks required also goes on changing (increasing). 
n is an example of a variable. Its value is not fixed; it can take any value 1, 2, 3, 4, ... . We wrote the rule for the number of matchsticks required using the variable n.
The word ‘variable’ means something that can vary, i.e. change. The value of a variable is not fixed. 
It can take different values.
Examples of variables : We have used the letter n to show a variable. There is nothing special 
about n, any letter can be used. One may use any letter as m, l, p, x, y, z etc. to show a variable. Remember, a variable is a number which does not have a fixed value. For example, the number 5 or the number 100 or any other given number is not a variable. They have fixed values. Similarly, the number of angles of a triangle has a fixed value i.e. 3. It is not a variable. The number of corners of a quadrilateral (4) is fixed; it is also not a variable. But n in the examples we have looked is a variable. It takes on various values 1, 2, 3, 4, ... .    

Let us take other example of variable : Raju and Balu are brothers. Balu is younger than Raju by 3 years. When Raju is 12 years old, Balu is 9 years old. When Raju is 15 years old, Balu is 12 years old. We do not know Raju’s age exactly. It may have any value. Let x denote Raju’s age in years, x is a variable. If Raju’s age in years is x, then Balu’s age in years is (x – 3). The expression (x – 3) is read as x minus three. As you would expect, when x is 12, (x – 3) is 9 and when x is 15, (x – 3) is 12.

Expressions with Variables
To form expressions we use all the four number operations of addition, subtraction, multiplication and division. For example, to form (2 × 10) + 3, we have multiplied 2 by 10 and then added 3 to the product. Expressions can be formed from variables too. In fact, we already have seen expressions with variables, for example: 2n, 5m, x + 10, x – 3 etc. These expressions with variables are obtained by operations of addition, subtraction, multiplication and division on variables. For example, the expression 2n is formed by multiplying the variable n by 2; the expression (x + 10) is formed by adding 10 to the variable x and so on.
One important point must be noted regarding the expressions containing variables. A number expression like (4 × 3) + 5 can be immediately evaluated as (4 × 3) + 5 = 12 + 5 = 17. But an expression like 
(4x + 5), which contains the variable x, cannot be evaluated. Only if x is given some value, an expression like (4x + 5) can be evaluated. For example, when x = 3, 4x + 5 = (4 × 3) + 5 = 17 as found above.

Ex.1     Give expressions for the following cases.
(a)     Rita scores x marks in Maths and 46 marks in English. What is her total score in Maths and English. 
 (b)     The difference of x and 9 where x > 9.
(c)     The product of a and b  added to the difference of a and b (a > b).
(d)     One-half of a multiplied by the sum of x and y.

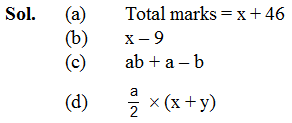
Ex.2 Ali is x years old. Express the following in algebraic form : 
(a)     4 times Ali's age 3 years hence. 
(b)      The present age of Ali's aunt who is four times as old as Ali will be 5 years from today. 
(c)     The present age of Ali's father who is 5 times as old as Ali was 3 years ago. 

Sol.   (a)     Ali's age 3 years hence = (x + 3) years 4 times Ali's age 3 years hence = 4(x + 3) years. 
(b)      Ali's age after 5 years = (x + 5) years. Ali's aunt age = 4 (x + 5) years   
(c)     Ali's age before 3 years = (x – 3) years. Ali's father age = 5(x – 3) years

Expressions and Equations

Expressions using variables

Terms of an Expression

 Parts of an expression that are formed independently first and again added or deducted are known as terms.

 In the above- given instance, terms 2x and 5 are added to form the expression (2x+5).

 Factors of a term

 Parts of an expression that are formed independently first and also added or deducted are known as terms.

 Factors of a term are amounts that cannot be further factorised.

 In the above- given instance, factors of the term 2 x are 2 and x.

 Coefficient of a term

 The numerical factor of a term is called the measure of the term.

 In the above- given illustration, 2 is the coefficient of the term 2x.

 Like and Unlike Terms

 Like terms

 Illustration 8xy and 3xy are like terms.

 Unlike terms

 Terms having different variables are called, unlike terms.

 Illustration 7xy and-3 x are unlike terms.

 Formation of an expression

Formation of Algebraic Expressions
Combinations of variables, constants, and operators constitute an algebraic expression.

 Illustration 2x+ 3, 3y +4xy, etc.

 Addition and Deduction of Algebraic Expressions

Addition and Deduction of like terms

Sum of two or more like terms is a like term.

 Its numerical measure will be equal to the sum of the numerical coefficients of all the like terms.

 

Example 8y + 7y =?
             8y + 7y
 (8 +7) y = 15y

 Difference between two like terms is a like term.

  Its numerical measure will be equal to the difference between the numerical coefficients of the two like terms.

 Illustration 11z − 8z =?

11z

 − 8z

 

 

(1- 8) z = 3z

 

 Addition and Deduction of unlike terms

 For adding or deducting two or more algebraic expressions, as if terms of both the expressions are grouped together and unlike terms are retained as it is.

Addition of − 5x² +12xy and 7x² + xy +7x is shown below

 − 5x² + 12xy

             7x² + xy +7x

 

 

 2x² +13xy+ 7x

 Deduction of − 5x² 12xy and 7x² xy 7x is shown below

 − 5x² +12xy

 − 7x² +xy +7x

 

 

  12 x 2 11xy − 7x

 

Expressions written in situations

Using Expressions Practically

The use of expressions comes handy in everyday. For e.g. if we know that the price of one kg onion is Rs.5 less than the price of 1kg potato, then we can use expressions to calculate the price of 1kg onion. Let the price of 1kg potato be x. Then the price of 1kg onion if Rs. (x-5).

Similarly, 1. If Seema is 5 years older than Ritu and the age of Ritu is given to be z years. Then Seema’s age is (z + 5) years.

Examples:

Problem: Answer the following:

Take Sarita’s present age to be y. 

What will be her age 5 years from now?
Her age 5 years from now will be = (y +5) years.
What was her age 3 years back?
Her age 3 years back was = (y – 3) years.

Sarita’s grandfather is six times her age. What is the age of her grandfather?

Age of Sarita’s grandfather = (6*y) years

 3. Grandmother is 2 years younger than grandfather is. What is grandmother's age?

 Age of Sarita’s grandmother = (Age of grandfather – 2) years

                                                  = (6*y -2) years
4. Sarita’s father’s age is 5 years more than 3 times Sarita’s age. What is?
Her father's age 

Age of Sarita’s father = (3y + 5) years.

5. A rectangular box has height h its length is 5 times the height and breadth is 10 cm less than the length. Express the length and the breadth of the box in terms of the height.

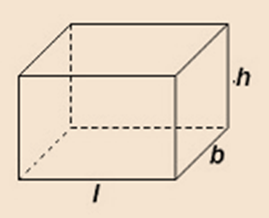
Height of rectangular box = h cm. (given)

Length of rectangular box = 5*h cm

Breadth of rectangular box = (Length – 10) cm

                                        = (5*h -10) cm.

6. A bus travels at v km per hour. It is going from Dasburg to Beespur. After the bus has travelled 5 hours, Beespur is still 20 km away. What is the distance from Dasburg to Beespur? Express it using v.

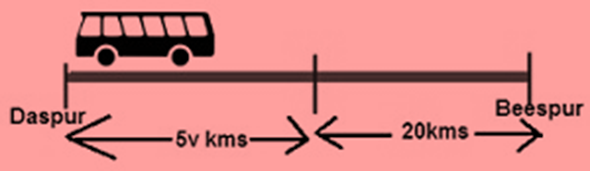
Speed of the bus = v km per hour

Distance travelled in 5 hours = Speed*Time

                                          = Speed (km per hour)* 5 hours

                                          = 5v kms

Distance from Dasburg to Beespur =Distance travelled in 5 hours + 20km

                                                 = (5v + 20) kms

What is an equation?

An equation is a condition on a variable, which is satisfied only for a definite value of the variable.

An equality sign separates the left- hand side (LHS) and right- hand side (RHS) of an equation. Hence LHS = RHS.

However, again, it is not an equation; If LHS is not equal to RHS.

Working an Equation

Value of a variable in an equation, which satisfies the equation, is called its result.

Solution to equations

One of the simplest methods of finding the solution of an equation is the trial and error method.