Chapter 13: Symmetry

hhhh

Introduction
Symmetry is quite a common term used in day to day life. When we see certain figures with evenly balanced proportions, we say, “They are symmetrical”.
Suppose we could fold a picture in half such that the left and right halves match exactly then the picture is said to have line symmetry (Fig). We can see that the two halves are mirror images of each other. If we place a mirror on the fold then the image of one side of the picture will fall exactly on the other side of the picture. When it happens, the fold, which is the mirror line, is a line of symmetry (or an axis of symmetry) for the picture.

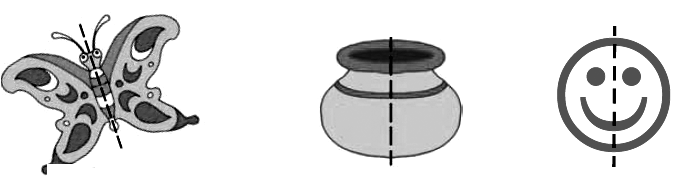
When we fold them along the dotted line, one half of the drawing would fit exactly over the other half.
 

Symmetry is quite a common term used in day to day life. When we see certain figures with evenly balanced proportions, we say, “They are symmetrical”.

These pictures of architectural marvel are beautiful because of their symmetry. Suppose we could fold a picture in half such that the left and right halves match exactly then the picture is said to have line symmetry.

 

Chapter 13

Symmetry

Introduction to symmetry

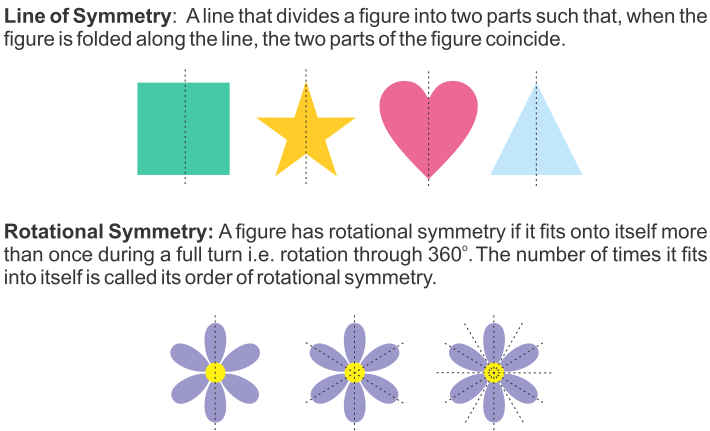
In geometry, symmetry is defined as a balanced and proportionate similarity that is found in two halves of an object. It means one-half is the mirror image of the other half. The imaginary line or axis along which you can fold a figure to obtain the symmetrical halves is called the line of symmetry.
If an object is symmetrical, it means that it is equal on both sides. Suppose, if we fold a paper such that half of the paper coincides with the other half of the paper, then the paper has symmetry. 

Symmetry can be defined for both regular and irregular shapes. For example, a square is a regular (all sides are equal) and a rectangle is an irregular shape (since only opposite sides are equal). The symmetries for both shapes are different

Two lines of symmetry

Line Symmetry

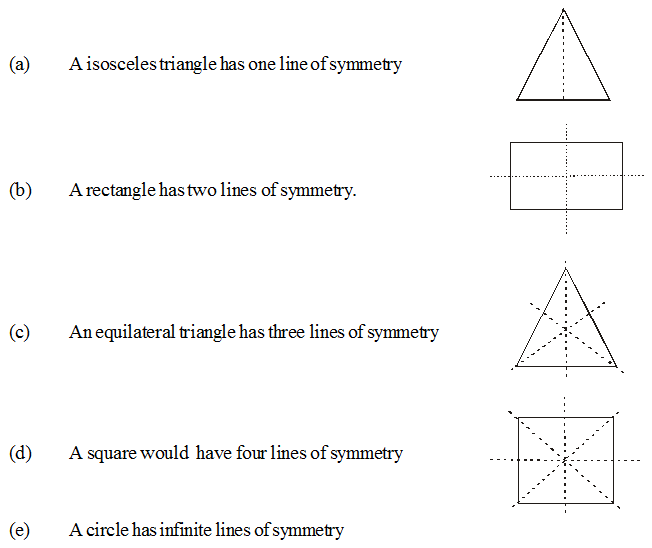
Figure is symmetrical only about one axis. It may be horizontal or vertical. The word ATOYOTA has one axis of symmetry along the axis passing through Y.

Figure is symmetrical with only about two lines. The lines may be vertical and horizontal lines as viewed in the letters H and X. Thus, we can see here two lines symmetry.

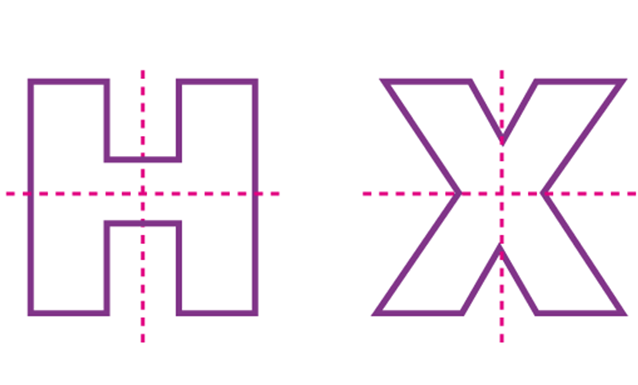
Three or more lines of symmetry

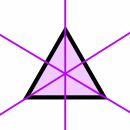
An example of three lines of symmetry is an equilateral triangle. Here, the mirror line passes from the vertex to the opposite side dividing the triangle into two equal right triangles.

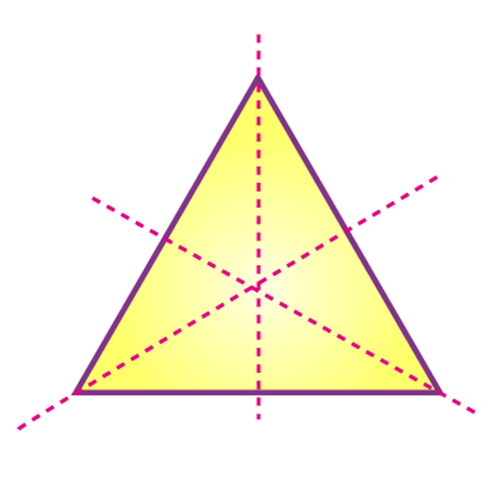
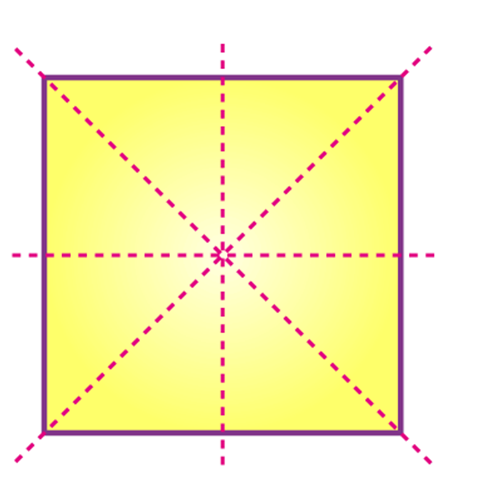
Four lines of symmetry can be seen in a square, which has all the sides equal. 

Reflection symmetry

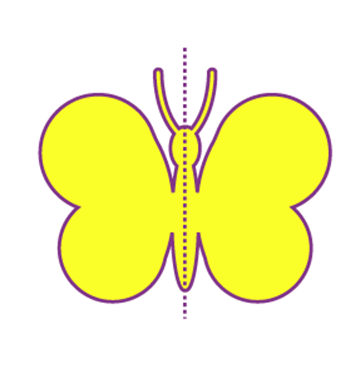
Reflection symmetry is a type of symmetry in which one-half of the object reflects the other half of the object. It is also called mirror symmetry or line of symmetry. A classic example of reflection symmetry can be observed in nature, as represented in the below figure.

 

Reflection Symmetry
If we draw a vertical line at the middle, the portions on either side of the line are identical. Similarly, in nature we find many flowers, leaves, etc., that have two identical sides if we draw a line through the middle of them.

Mirror  Symmetry
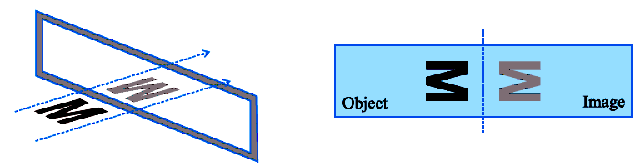
Reflection symmetry is the symmetry with respect to reflection. If a mirror is placed along the line at the middle, the half part of the figure reflects through the mirror creating the remaining identical half. In other words, the line where the mirror is placed divides the figure into two identical parts  they are of the same size and also every specific part on one side of the line will have its reflection exactly at the same distance on the other side. Thus, it is also known as mirror symmetry or mirror image symmetry.
Here is a picture showing the reflection of the English letter M. You can imagine that the mirror is invisible and can just see the letter M and its image.

 

Reflection Symmetry

Reflection Symmetry (sometimes called Line Symmetry or Mirror Symmetry) is easy to see, because one half is the reflection of the other half.

 

 

Here my dog "Flame" has her face made perfectly
symmetrical with a bit of photo magic.

The white line down the center is the Line of Symmetry
(also called the "Mirror Line")

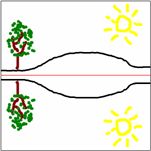
The reflection in this lake also has symmetry, but in this case:

• the Line of Symmetry runs left-to-right
• it is not perfect symmetry, because the image is changed a little by the lake surface.

Line of Symmetry

 

The Line of Symmetry (also called the Mirror Line) can be in any direction.

But there are four common directions, and they are named for the line they make on the standard XY graph.

See these examples (the artwork was made using Symmetry Artist) :

Line of Symmetry

Sample Artwork

Example Shape

 

 

 

 

 

 

 

 

 

Plane Shapes

Not all shapes have lines of symmetry, or they may have several lines of symmetry. For example, a Triangle can have 3, or 1 or no lines of symmetry:

 

 

Equilateral Triangle
(all sides equal,
all angles equal)

 

Isosceles Triangle
(two sides equal,
two angles equal)

 

Scalene Triangle
(no sides equal,
no angles equal)

3 Lines of Symmetry

 

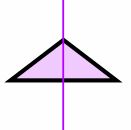
1 Line of Symmetry

 

No Lines of Symmetry

 

Asymmetrical figure
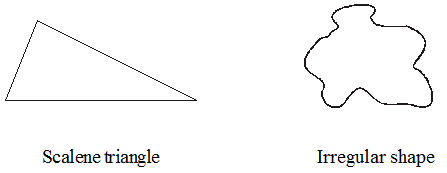
Some  objects and figures have no line of symmetry, a scalene triangle is not symmetrical. We can say that a scalene triangle is asymmetrical. The irregular shapes have no line of symmetry.

Figures with Multiple (more than two) Lines of Symmetry
Some objects and figures have more than one line of symmetry.