- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Types of Fractions
(i) Proper Fractions : A proper fraction is a fraction in which the numerator is smaller than the denominator.

(ii) Improper Fractions : An improper fraction is a fraction in which the numerator is greater than the denominator.
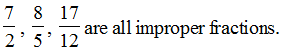
(iii) Mixed fraction : Fractions such as ![]() are called Mixed Fractions. A mixed fraction has a combination of a whole and a part.
are called Mixed Fractions. A mixed fraction has a combination of a whole and a part.
Ex. Express the following as mixed fraction :
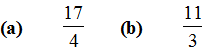
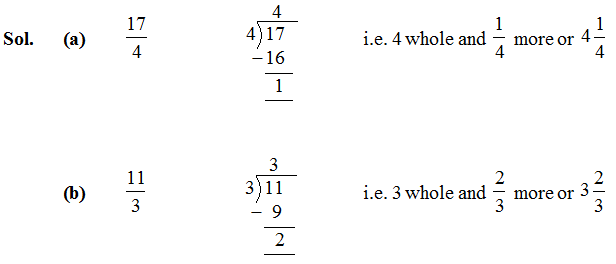
Conversion of Mixed Fractions into Improper Fractions

- Books Name
- Class 6 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 6
- Subject
- Mathmatics
Fraction and its Classification
Fraction and its types,
It has to be noted that while expressing a situation of counting region to write a fraction, all region must be equal.

Then, three is called the numerator and 4 are called the denominator.
Numerator and denominator can be linked for any fraction.
The upper part of the fraction is called Numerator.
It tells the number of region we have.
The lower part of the fraction is called Denominator.
It tells the total region in a whole.
It reads as" three- fifths"
Proper and Improper fraction,
Proper Fractions
If the numerator is bigger than the denominator then it's called proper bit. If we represent a proper bit on the number line than it'll always lie between 0 and 1.
Example:
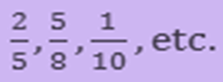
Improper fractions and mixed fractions
When the numerator is bigger than the denominator then it's called Improper bit.
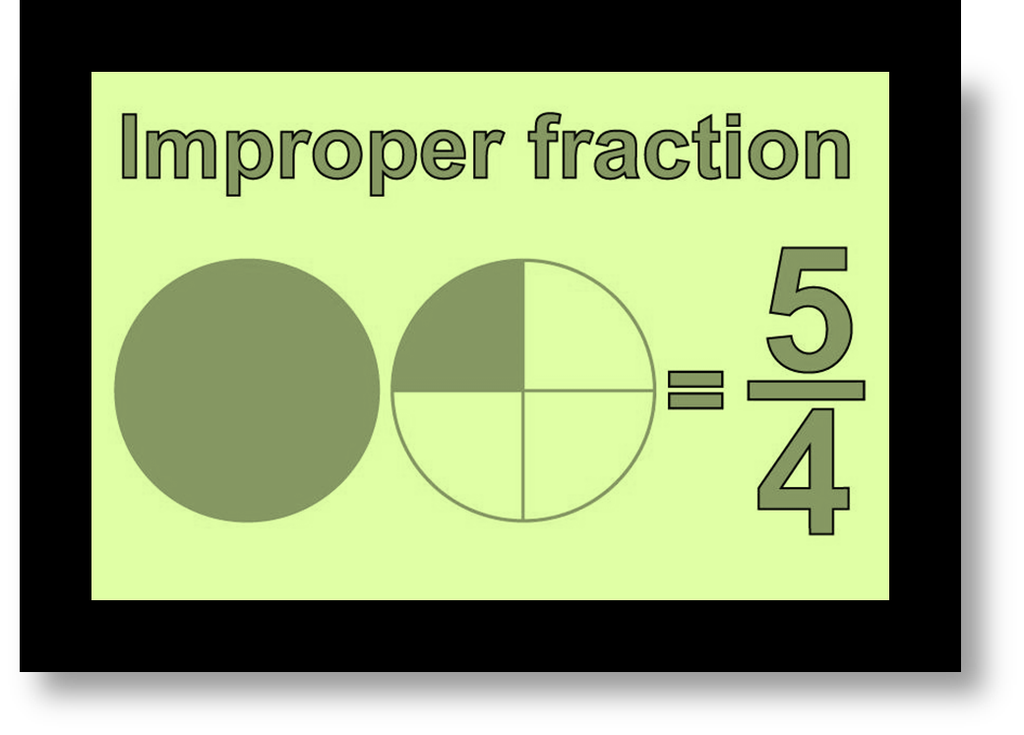
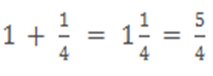
The above fraction is made by adding one whole part and one- fourth part.
Mixed Fraction
The bit made by the combination of whole and a part is called mixed bit.
Convert mixed bit into improper bit
A mixed bit is in the form of
Fractions

We can convert it in the form of an improper fraction by
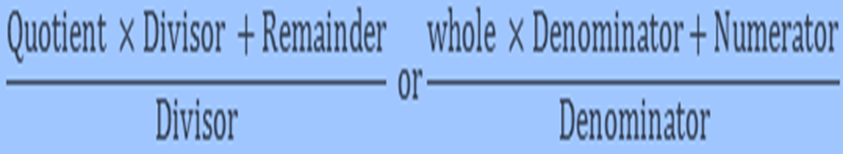
Example

Answer
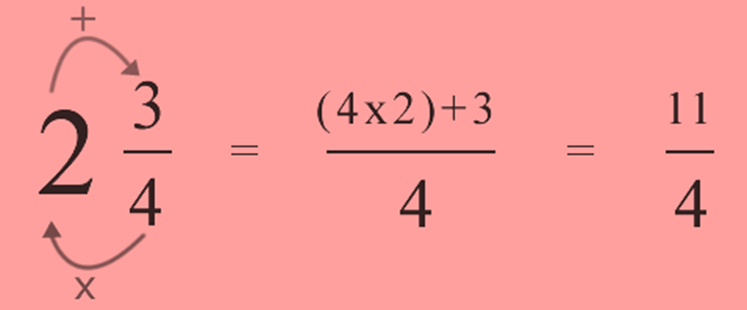
Like fractions and unlike fractions
Fractions that have same denominators are known as Like fractions.
Equivalent fraction
Equivalent fractions
Equivalent fractions are those fractions which represent the same part of a whole.
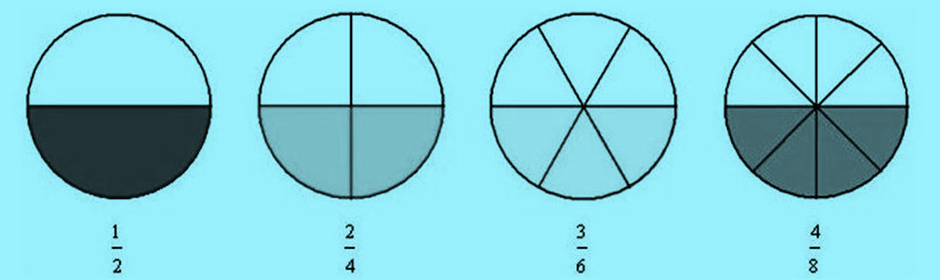
All the above images are different but Equivalent fractions as they represent the same i.e. half part of a whole circle.
Finding Equivalent fractions:
Multiplying the same number
If we multiply the numerator and denominator of any bit with the same number then we will get the Equivalent bit. There could be other than one Equivalent fractions of one bit.
Example
Find three Equivalent fractions of ½.
Answer:
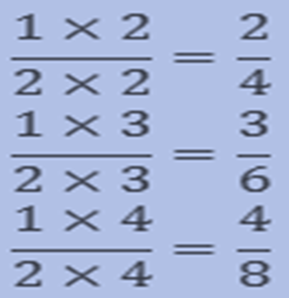
Dividing the same number
If we divide the numerator and denominator of any bit with the same number then we will get the Equivalent fractions.
Example
Find the Equivalent fraction of 18/27 with denominator 9.
Answer
To get the denominator 9 we need to divide it by 3.
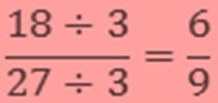
Therefore, to find the Equivalent fraction we need to divide the bit by 3.
Hence, the Equivalent fraction with denominator 9 is 6/9.
The simplest form of a fraction
If the numerator and denominator don't have any other common factor than 1 then it's said to be the simplest or smallest form of that bit.
Example-
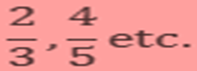
To find the Equivalent fraction which is the simplest form we've to find the HCF of numerator and denominator and then divide them both by that HCF.
Example
Reduce the fraction18/27 in the simplest form.
Answer
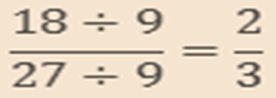
HCF of 18 and 27 is 9.
Hence, 2/3 is the smallest form of18/27.
Simplest form of fraction
Fractions that have different denominators are known as unlike fractions.
Example

Comparing fractions
If we've to compare the above two fractions then it's easy as the first one is lower than 3 and the alternate bone
is bigger than 3. So we can easily say that
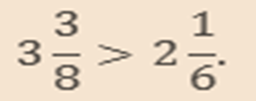
But occasionally it isn't easy to compare it so fluently. So we need some accurate procedure.
Comparing like fractions
Like fractions are the fractions with the same denominator so we've to compare them with the numerator only. The fraction with bigger numerator is bigger.
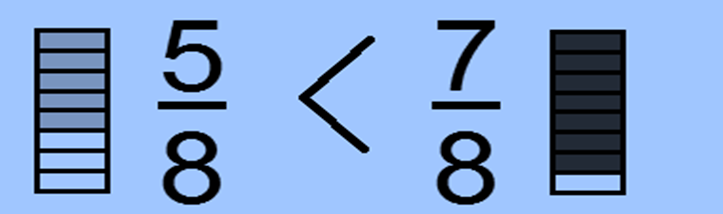
In the above example, both are divided into 8 equal corridors, so the bit with seven-shadowed part is bigger than the 5-shadowed corridor.
Comparing unlike fractions
The fractions with different denominators are unlike fractions.
Unlike fraction with the same numerator
Still, we have to compare with the denominator only, if we have to compare the fractions with different denominator but same numerator.
In that case, the bit with the small denominator is bigger than the other.
Example
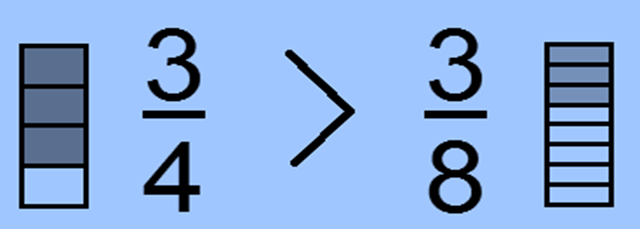
Then the numerator is same i.e. 3 so we will compare with the denominator.
The bit with small denominator i.e. ¾ is bigger than the bit with the large denominator i.e.3/8.
Unlike fraction with different numerators
If the numerator and denominator both are different then we have to make the denominator same by finding the Equivalent fraction of both the fractions then compare the fractions as like fractions.
To find the Equivalent fraction of both the fractions with the same denominator, we've to take the LCM of the denominator.
Example
Compare 6/7 and3/5.
Answer
The product of 7 and 5 is 35.
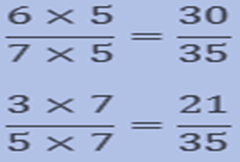
Therefore, we will find the Equivalent fraction of both the fractions with the denominator 35.

Now we can compare them as like fractions.

 Param Publication
Param Publication
 ReginaTagebücher
ReginaTagebücher
