2. Quadrilaterals, Polygons and Three Dimensional Shapes

Line Segment
A line segment is a fixed portion of a line. This makes it possible to measure a line segment. This measure of each line segment is a unique number called its “length”. We use this idea to compare line segments.
To compare any two line segments, we find a relation between their lengths.
This can be done in several ways.
(i)     Comparison by observation: The method of comparing two segements by observations is not always correct. Therefore, we need a better method. 
(ii)     Comparison using Ruler and a Divider : 
(a)     Using a Ruler : Suppose we have to measure the length of a given   segment AB. Take a ruler with centimeter marks and place it along the segment AB such that the 

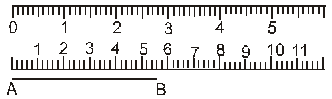
zero mark on the ruler is just at A as shown in the figure. Now read the mark on the ruler which corresponds to B. In this figure we see that the mark corresponding to B is the eighth small division after 5, i.e. AB contains 5 full centimeters and 8 millimeters. We say that the length of AB is 5.8 cm and write it as AB = 5.8 cm. 

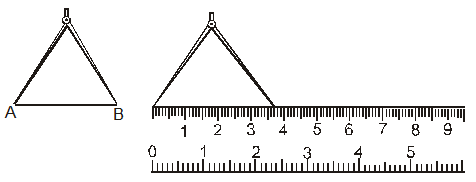
(b)    Using a Divider : We open the divider such that the point of one arm is at A and the second exactly at B, i.e. the segment AB is contained in the divider. Now lift the divider carefully without disturbing its opening and place it on the ruler so that one point of the divider is at zero (0) mark. We then read the mark which corresponds to the second point of the divider. 
In the adjoining figure the second point of the divider is at the seventh mark after 3, 
i.e. AB contains 3 complete centimetres and seven-tenths of a centimetre. We say that AB is 3 cm and 7 mm and write it as AB = 3.7 cm. 

Units for measurment of line segments :The unit of measurment of length is metre.
A metre is divided into 100 equal  parts, each called a centimetre. A centimetre is further subdivided into  10 equal parts, each called a millimetre.    
Thus we have the following table :
          10 Millimetres (mm) = 1 Centimetre (cm)
          10 Centimetres(cm) = 1 Decimetre (dm)
          10 Decimetres (dm) = 1 Metre (m)
 or ,    1 metre  = 10 decimetres
                        = 100 centimetres 
                        = 1000 millimetres 

Ex.    If B is the mid point of AC and C is the mid-point of BD where A, B, C and D are collinear, show that AB = CD ?

Sol.     B is the mid-point of AC
        ∴     AB = BC                   .....(i)
            Again C is the mid-point of BD
            CD = BC                  .....(ii)            
            From (i) and (ii), we get 
            AB = CD

 

Quadrilaterals, Polygons and Three Dimensional Shapes

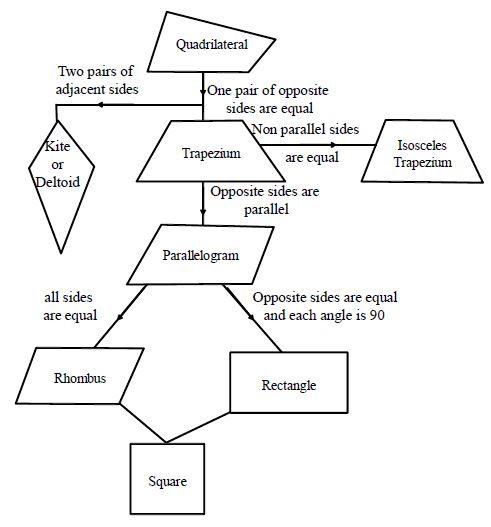
QUADRILATERALS
A closed figure surrounded by four line segments is called a quadrilateral.
A  quadrilateral ABCD has:
Four vertices, named as A, B, C and D
Four sides, named as AB, BC, CD and DA
Four angles, named as  angle A, angle B, angle C and angle D
Two diagonals, named as angle AC and angle BD

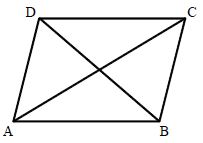
Adjacent Sides
Two sides of a quadrilateral triangle are having a common close (end) point are known as triangle’s adjacent or consecutive sides. In the quadrilateral given below, There are four pairs of its adjacent sides. (AB, BC), (BC, CD), (CD, DA) and Opposite Sides are (BA, AD)
opposite sides of the triangle are defined as the Two sides of the quadrilateral are having no common end point.

In the quadrilateral (AB, CD) and (BC, AD) are opposite sides of its two pairs.

Adjacent Angles

Two angles of a quadrilateral that are having a common section are called its adjacent or consecutive angles. In the quadrilateral (angle A, angle B), (angle B, angle C), (angle C, angle D) and (angle D, angle A) are four pairs of adjacent angles of triangle

Opposite Angles
Two angles of a quadrilateral triangle are not having a common section are called its opposite angles of triangle.
In the quadrilateral (angle A, angle C) and (angle B, angle D) are two pairs of its opposite angles of triangle.
The sum of all the angles of a quadrilateral triangle is 360°.
The sum of exterior angles of a quadrilateral triangle is 360°.
Parallelogram
A quadrilateral triangle in which two pairs of opposite sides are parallel is called a parallelogram.

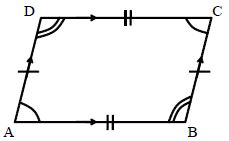
In a Parallelogram:
Opposite sides are equal
Opposite angles are equal
each diagonal bisects the parallelogram
when pair of opposite sides of a Quadrilateral triangle are equal and parallel, it is a parallelogram
Rectangle: A parallelogram each of their angle having size of 90° is called a Rectangle.

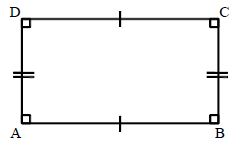
In a Rectangle:
Opposite sides are equal
each angle measure is 90°
Diagonals are equal
Diagonals bisect each other
Square: A Rectangle that has all sides equal is known as a square. When two adjoining sides of a Rectangle are equal, then it is known as a Square
 

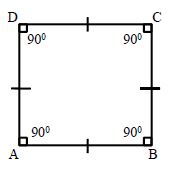
In a Square:
All sides are equal
Each angle measures 90°
Diagonals are equal
Diagonals bisect each other
Diagonals intersect at right angles
Rhombus: A parallelogram that have all sides equal is known as a Rhombus
 

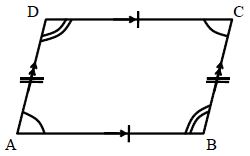
In a Rhombus:
Opposite sides are parallel
All sides are equal
All Diagonals cut across  each other at right angles of triangle
Trapezium: A Quadrilateral  in which two opposite facing sides are parallel is known as a trapezium. In diagonal divides proportionally
 

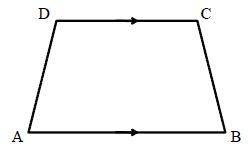
when the (unequal) non parallel sides of a trapezium are equal. It is called as isosceles-trapezium
Kite: The Quadrilateral in which two pairs of the adjacent sides are equal is called as a kite. The longer diagonal intersects the shorter diagonal.

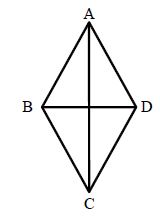
Relation between Quadrilaterals

POLYGONS

A closed plane image enclosed by three or more line segments is known as a polygon. The line sections that form a polygon are called its sides. The point of intersection of two following sides of a polygon is known as a vertex.

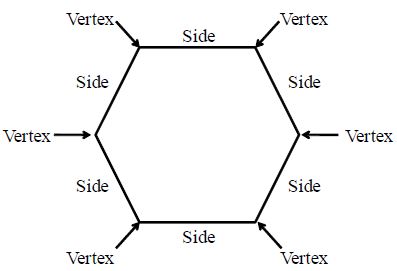
The total number of vertices of a polygon is always equal to the number of its sides.

A polygon of n-sides is called n-gon. Thus, a polygon of 20 sides is a 20-gon

Diagonal of a Polygon
A line segment that join with any two non-consecutive vertices of a polygon is called diagonal of polygon. Therefore, in the figure ABCDE is a polygon image and each of the line segments AC, AD, BD, BE and CE is the diagonal of the polygon.

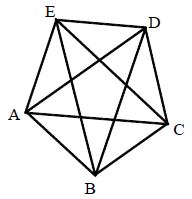
Interior and Exterior Angle of a Polygon:
An angle made by the two consecutive (following) sides of the polygon is known as an interior angle or we can say that an angle of the polygon.

Name of Polygon	Number of sides	Number of Triangles formed	Angle sum of polygon
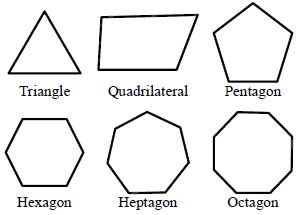
Triangle	3	1	1×180°=180°1×180°=180°
Quadrilateral	4	2	2×180°=360°2×180°=360°
Pentagon	5	3	3×180°=540°3×180°=540°
Hexagon	6	4	4×180°=720°4×180°=720°
Heptagon	7	5	5×180°=900°5×180°=900°
Octagon	8	6	6×180°=1080°6×180°=1080°
Nonagon	9	7	7×180°=1260°7×180°=1260°
Decagon	10	8	8×180°=1440°8×180°=1440°
Undecagon	11	9	9×180°=1620°9×180°=1620°
Dodecagon	12	10	10×180°=1800°10×180°=1800

From this s table, we can see that the number of triangles formed in a polygon is two smaller than the number of sides. So for a polygon with n sides, the number of triangles formed is n – 2.

A polygon with n sides has the angle sum :( n – 2) × 180°.

Hence, S = (n – 2) 180°.
In a regular polygon with n sides each inside angle is equal to (n–2) ×180n (n–2) ×180n
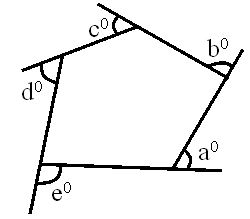
When each side of a polygon is produced (extended) in a clockwise or anti clockwise direction, surface (outer part of the angel) angles are formed as shown.
The sum of the exterior angles of any polygon is 360°.

THREE DIMENSIONAL Figures
Solid State Figures: Figures with height/density (thickness), length, breadth and are called solids.
Cuboids: The solid in rectangular shape having the four slanting sides with top and base are called ‘cuboids’. The solid formed by six rectangular surfaces is called cuboids

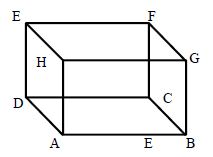
E.g.: Bricks, Eraser.
Number of surfaces = 6
Number of vertices = 8
Number of edges = 12
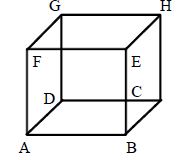
Cube: A Solid formed by the enclosure of six square plane surfaces is called a ‘cube’. Cube has – six faces, eight vertices, twelve edges.

Cylinder: The figures which have top and base are circular in shape. The remaining surface is called curved surface.

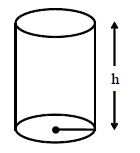
Cone: The base is a circle. Its radius is denoted by r. ACAC is called slant height and it is denoted by‘s’. AOAO is called vertical height and it is denoted by ‘h’. A is called its vertex.

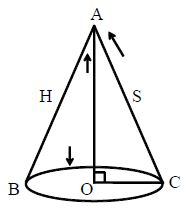
Sphere: Ball, Marbles and balls in the cycle bearings are some of examples of Sphere. In the below figure, ‘centre’ is called as O.  AOAO is called its radius. Its surface is called curved surface.

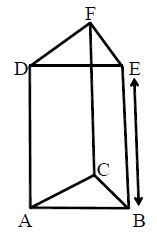
Prism: Triangular Prism. The adjoining figure shows a ‘triangular prism’. (Its base is a triangle) It is the shape of its base. It has six vertices and five surfaces.

Pyramid:  Pyramid figures base is in square shape and their lateral faces are in triangular shape, such that all the four surfaces meet at one point.
The below figure tells about square ABCD as its base in the pyramid shape.
AB =BC=CD=DA = aAB¯=BC¯=CD¯=DA¯=a, shows the side of its base.

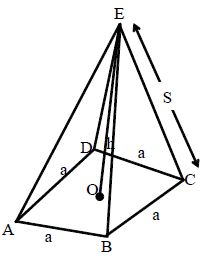
EOEO = h is called its vertical height. ECEC = s is called its slant height or lateral height. There are five surfaces with the square base and four triangular shaped surfaces all together.
Triangular Pyramid: If a pyramid has triangular base, then it is called a ‘triangular pyramid’. It has one triangular base and three triangular lateral surfaces. All together the triangular pyramid has four triangular faces.

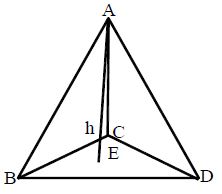
The adjoining figure shows a ‘triangular pyramid’. Its base is a triangle BCD. Lateral height of each triangle (lateral surfaces) is called the slant height which is denoted as s and the point of meeting all the lateral sides. ‘Apex or vertex’ is denoted by ‘A’. 

AEAE = h is called height.