3. Estimation of Numbers

USING BRACKETS
Meera bought 6 notebooks from the market and the cost was Rs 10 per notebook. Her sister Seema also bought 7 notebooks of the same type. Find the total money they paid.
Seema calculated the 
6 × 10 + 7 × 10 = 60 + 70 = 130 
Meera calculated the amount like this amount like this
6 + 7 =13  and 13 × 10 = 130
 Ans. Rs 130.

We can see that Seema’s and Meera’s ways to get the answer are a bit different. 
To avoid confusion in such cases we may use brackets. We can pack the numbers 6 and 7 together using a bracket, indicating that the pack is to be treated as a single number. 
Thus, the answer is found by (6 + 7) × 10 = 13 × 10.
First, turn everything inside the brackets ( ) into a single number and then do the operation outside which in this case is to multiply by 10.

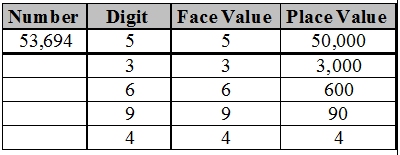
FACE VALUE
Face value of a digit in a numeral is the value of the digit itself at whatever place it may be. 

PLACE VALUE
Place value of a digit in a given number is the value of the digit because of the place or the position of the digit in the number.
Place value of a digit = Face value of the digit  × value of the place  

Place value and Face value :
Every digit has two values – the place value and the face value. The face value of a digit does not change while its place value changes according to its position and number. 

Expanded form of a Number :
If we express a given number as the sum of its place value, it is called its expanded form. 

Ex:    Express 
        (i) 3,64,029    (ii) 2,75,00,386 in expanded form. 
Sol.  Place value of 3 = 3 x 100000 
        Place value of 6 = 6 x 10000
        Place value of 4 = 4 x 1000
        Place value of 0 = 0 x 100
        Place value of 2 = 2 x 10 
        Place value of 9 = 9 x 1
 ∴    The expanded form of 3,64,029 is  
        3 x 100000 + 6 x 10000 + 4 x 1000 + 0 x 100 + 2 x 10 + 9 x 1.    

Look and Guess the Number

Estimation

The estimation of a number is a reasonable approximation of the real value. Estimation means approaching an amount to the closeness needed. This is done by rounding off the figures involved and getting a quick and rough answer.

Rounding off a number to the nearest tens numbers

The numbers 1, 2, 3, 4   are nearest to 0. So, these numbers are rounded off to smaller ten. The numbers 6, 7, 8, 9 are nearest to 10. So, these numbers are rounded off to the bigger tens. The number 5 is nearest from both 0 and 10, so it's rounded off to the advanced ten.

e.g.

(i) We round off 41 to the nearest ten as 40

(ii) We round off 67 to the nearest ten as 70

(iii) We round off 55 to the nearest ten as 60

Rounding off a number to the nearest hundreds number

The numbers 201 to 249 are closer to 200. So, these numbers  are rounded off to the nearest hundred i.e. 200. The numbers 251 to 299 are closer to 300. So, these numbers are rounded off to the advanced hundred i.e. 300. The number 250 is rounded off to the advanced hundred.

(i) We round off 678 to the nearest 100 as 700.

(ii) We round off 510 to the nearest 100 as 500.

  Rounding off a number to the nearest thousands number

Also, 1001 to 1499 are rounded off to the lower thousand i.e. 1000, and 1501 to 1999 to the advanced thousand i.e. 2000. The number 1500 is equidistant from both 0 and 1000, and so it's rounded off to the advanced thousand i.e. 2000.

 (i) We round off 3574 to the nearest thousand as 4000.

 (ii) We round off 8105 to the nearest thousand as 8000.

Estimation of sum or difference

When we estimate sum or difference, we should have an idea of the place to which the rounding is demanded.

e.g.

 (i) Estimate 5798 + 29834

 We can say that 29834 > 5798

 We shall round off the figures to the nearest thousands.

29416 is rounded off to 30000

 5679 is rounded off to 6000

Estimated sum

49000 + 3000 = 52000

 (ii) Estimate 2476 – 946

We shall round off these figures to the nearest hundreds.

2476 is rounded off to 2000

946 is rounded off to 1000

Estimated difference

2000 – 1000 = 1000

 Estimation of the product

To estimate the product, round off each factor to its topmost place, also multiply the rounded off factors.

 Estimate 82 x 578

 The first number, 82, can be rounded off to the nearest ten as 80.

The alternate number, 678, can be rounded off to the nearest hundred as 700.

 Hence, the estimated product = 80 x 700 = 56000.

Using Brackets

 

Brackets help in simplifying an expression that has multiple operations. If any statement that includes the brackets is there, then perform the operation inside the bracket first and simplify each number in to a single number. Then carry out the operation that is outside the bracket.

e.g.
1. (6 8) x 10 = 14 x 10 = 140

2. (8 3) (9-4) = 11 x 5 = 55

Expanding Brackets

The use of classes allows us to follow a certain procedure to expand the classes totally.
E.g.
8 x 109 = 8 x (100 9) = 8 x 100 8 x 9 = 800 72 = 872
105 x 108 = (100 +5) x (100 + 8)
= (100+ 5) x 100 (100 + 5) x 8
= (100 x 100) (5 x 100) (100 x 8) (5 x 8)
= 10000 500 800 40
= 11340.

Brackets are used to reduce the confusion while solving the questions like add, subs tract, multiply and divide. For solving a bracket statement, first estimate and make a single number in the bracket and also estimate the outside part.

Problem:

(3+ 4) x 5 = (7) x 5 = 7 x 5 = 35

 This shouldn't be calculated as (3 4) x 5 = (3) 4x5.

Classes are expanded to estimate individual integers inside the classes with the integers outdoors.

 (3+ 4) x 5 = 3 x 5 4 x 5 = 15 20 = 35

 Problem: Write the expressions for each of the following using classes.

 Expression using words

 Expression using Figures and classes

 The number six is multiplied by the sum of seven and three

6 x (7 +3) OR (7 +3) x 6

  Divide the subtraction  of eighteen and six by four

(18-6)/ 4

 Divide eighty five by four times the sum of five and four

85/ ((4 +5) x 4)