Institute Updation Release 1.1

23/8/2021  4:45 PM

Notes

Publisher Update Release -> 23/8/2021  4:45 PM

Introduction

We use numbers and know many things about them. Numbers help us count concrete objects. They help us to say which collection of objects is bigger and arrange them in order e.g., first, second, etc. Numbers are used in many different contexts and in many ways. Think about various situations where we use numbers. List five distinct situations in which numbers are used. 
We have added, subtracted, multiplied and divided them. In this chapter, we shall move forward on such interesting things with a bit of review and revision as well.  

USE OF COMMAS
You must have noticed that in writing large numbers in the sections above, we have often used commas. Commas help us in reading and writing large numbers. In our Indian System of Numeration we use ones, tens, hundreds, thousands and then lakhs and crores. Commas are used to mark thousands, lakhs and crores. The first comma comes after hundreds place (three digits from the right) and marks thousands. The second comma comes two digits later (five digits from the right). It comes after ten thousands place and marks lakh. The third comma comes after another two digits (seven digits from the right). It comes after ten lakh place and marks crore.
Ex:    5, 08, 01, 592
         3, 32, 40, 781
         7, 27, 05, 062

Suppose a newspaper report states that Rs.2500 crore has been allotted by the government for National Highway construction. The same amount of Rs.2500 crore is sometimes expressed as Rs. 25 billion. In the Indian system, we express it as Rs. 2500 crore and in the International system, the same number is expressed as 25 billion. Hence we need to understand both the systems and their relationship.

Ascending order 
    Ascending order means arrangement from the smallest to the greatest.

Descending order 
    Descending order means arrangement from the greatest to the smallest.

Ex:    Arrange the following numbers in ascending order :
        257536, 38952, 385081, 365062
Sol.    The smallest number is 38952. Other numbers greater than 38952, in order are 257536, 365062 and 385081.
    ∴    The numbers in ascending order are  38952, 257536, 365062, 385081.    

    Ex:    Arrange the following numbers in descending order :  19710, 887151, 453212, 925473
    Sol.     The greatest number is 925473. Other numbers smaller than 925473 in order are 887151, 453212 and 19710.
    ∴   The numbers in descending order are 925473, 887151, 453212, 19710.]

We just looked at the number of digits and found the answer. The greatest number has the most thousands and the smallest is only in hundreds or in tens. Make five more problems of this kind and give them to your friends to solve. Now, how do we compare 4875 and 3542? This is also not very difficult. These two numbers have the same number of digits. They are both in thousands. But the digital the thousands place in 4875 is greater than that in 3542. Therefore, 4875 is greater than 3542. Next tell which is greater, 4875 or4542? Here too the numbers have the same number of digits. Further, the digits at the thousands place are the same in both. What do we do then? We move to the next digit, that is to the digit at the hundreds place. The digit at the hundreds place is greater in 4875 than in 4542. Therefore, 4875 is greater than 4542.

.90u9

Introduction:-

Counting Numbers: -The numbers which we can count. Like 1, 2, 3, 9, 37 etc.

Natural Numbers: -The numbers which we can count and it starts from 1 and goes on. Like 1, 2, 3, 4, …….100, …….2000, …………... etc.

Whole Numbers: -The counting numbers which starts from Zero are called whole numbers and goes on. Like 0, 1, 2, 3, 4, …….100, …….2000, …………... etc.

Integers: -Integers are the collection of whole numbers and negative numbers. Integers can be positive numbers, Zero and negative numbers but it cannot be a fraction. Like -229, -85, -16, -5, -1, 0, 1, 5, 29, 219, 5000 etc.

Even Numbers: -The numbers which are completely divisible by 2. It means those numbers which we divide by 2, remainder becomes Zero (0). Like 2, 4, 6, 22, 100, 294, 604 etc

Smallest Even number is 2.

Odd Numbers: - The numbers which are not completely divisible by 2. It means those numbers which we divide by 2, remainder becomes One (1). Like 1,3, 5, 7, 21, 101, 299, 1001 etc

Smallest Odd number is 1.

Composite Number: -A composite number is a natural number or positive integers which has more than two factors.

It means the given number is completely divisible by more than two numbers. Like 6, which is completely divisible by 1, 2, 3 and 6. It means 6 has four factors.

Example: - 4, 6, 8, 10, 12, 256 etc.

Smallest composite number is 4.It has three factors, these are 1,2, 4.

Prime Number: -A prime number is a natural number that is completely divisible by 1 and the number itself. Prime number has only two factors these are 1 and the number itself.

Like 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47 etc.

Smallest prime number is 2.

Twin Prime Number: -Two prime numbers are called twin prime, if there is present only one composite number between them.Like {3,5}, {5,7}, {11,13}, {17,19}, {29,31}, {41,43} etc. Two consecutive prime number can be twin primes.

{2,3} is not a twin prime number, because there is no composite number in between them.

Co-prime Number: -Two numbers are co-prime, if they have no common factor other than 1 or we can say that the HCF (Highest Common Factor) of these numbers is 1.Like {1,3}, {4,5}, {13,31}, {18, 35}, {15,17}, {29,30}.

It is not necessary that these numbers should be prime.

CHAPTER -1

KNOWING THE NUMBERS

 

Comparing  Shifting Digits, Revisiting Place Value and Large Numbers

Numbers are compared to check which Number is Greater or smaller than the other number. There are different ways to know that a number is smaller or Greater.

These are:

If the numbers used in the question is different. The number having next number is smaller and the other number is Bigger.

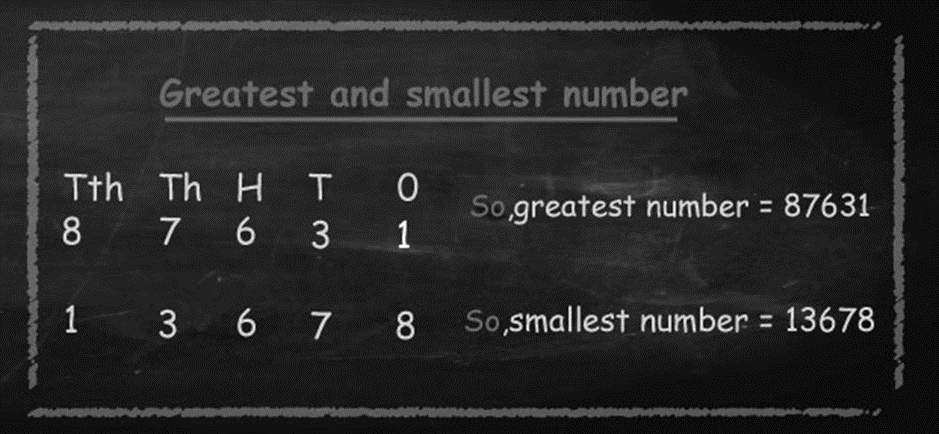
 For Example:  1. Find out Greatest Number from 125 and 120.

Solution: 125 is bigger number and 120 is smaller Number. Hence the number 125 is greatest.

 2. Find out greatest and smallest number from 320, 1340, 158, 228, 5446, and 4525

Solution: Here 5446 is the greatest and 158 is the smallest.

If the number of digits is equal than the number at the greatest place is compared.

 If the integers at the greatest place are different, the greater value is larger number and the smaller value is the smaller number.

 For Example: 1.Compare 285 and 685,

Solution: The numbers of integers are same, but number at greatest (then hundreds) place, is 2 and 6. Since 6 is greater number than 2, hence 685 is greater and 285 is smaller.

If the integers at the greatest place are equal, then another place is compared and so on.

For Example: 1. Compare 353 and 335.

Solution:  The number of integers and number at greatest place are same then we will check the second greatest number place and compare both the numbers. Since 5 is advanced than 3. Therefore 353 is greater number and 335 is smaller number

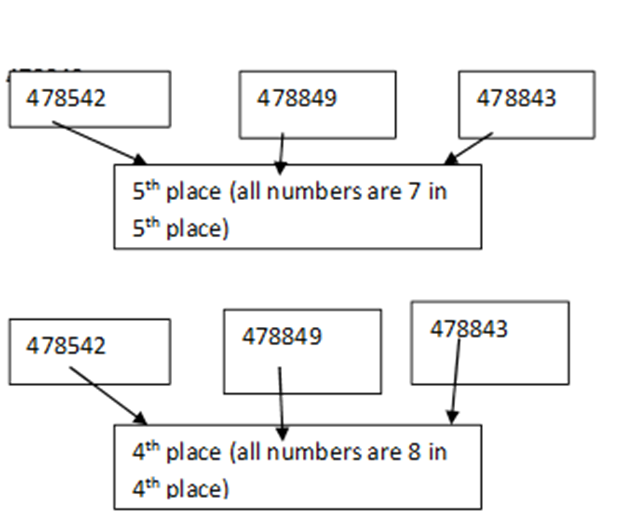
 2. Compare among 478542, 478849 and 478843.

Solution: There are same number of integers and number at the greatest integers places are same for last three positions (4th place numbers are same for all the numbers), (5th place numbers are same for all the numbers) and (6th place numbers are same for all the numbers) and 2nd place is also same for all the numbers).3rd place number is same for 

Second and third digit. So now we will compare first digit 3rd place number with another two numbers third place. Since 8 is bigger than 5.

 

 

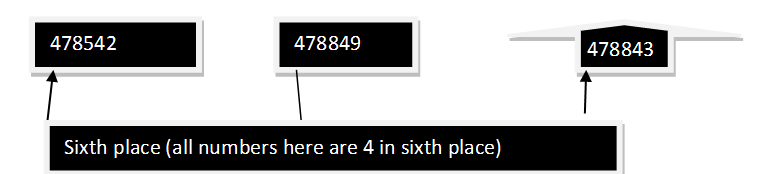
So 478542 is smaller number when compared 3rd position number (8 is greater than 5) with fist number to another two numbers.

Numerals

One of the early systems of writing numbers  is the system of Roman Numerals. This system is still used in different places. For Example, we can see the use of Roman Numerals in  Clock. It's also used in classes for the School time table.
Roman Numerals are expressed by seven letters of the Alphabets.

Rules of the System

The Roman  Numerals  I, II, III, IV, V, VI, VII, VIII, IX, X denote number 1 to 10 . Then

XI for 11,

XII for 12 … till XX for 20.
VI = 5 +1 = 6,

XII = 10 +2 = 12 and

LXV = 50 +10 + 5 = 65

Related Topic Name

2. Large Numbers in Practice
3. Estimation of Numbers