1. Numbers: Comparing, Shifting Digits, Revisiting Place Value and Large Numbers
Institute Updation Release 1.1
23/8/2021 4:45 PM
1. Numbers: Comparing, Shifting Digits, Revisiting Place Value and Large Numbers
- Books Name
- CBSE Mathematics for Class 6
- Publication
- Carrier Point
- Course
- CBSE Class 6
- Subject
- Mathmatics
Notes
1. Numbers: Comparing, Shifting Digits, Revisiting Place Value and Large Numbers
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Publisher Update Release -> 23/8/2021 4:45 PM
Introduction
We use numbers and know many things about them. Numbers help us count concrete objects. They help us to say which collection of objects is bigger and arrange them in order e.g., first, second, etc. Numbers are used in many different contexts and in many ways. Think about various situations where we use numbers. List five distinct situations in which numbers are used.
We have added, subtracted, multiplied and divided them. In this chapter, we shall move forward on such interesting things with a bit of review and revision as well.
USE OF COMMAS
You must have noticed that in writing large numbers in the sections above, we have often used commas. Commas help us in reading and writing large numbers. In our Indian System of Numeration we use ones, tens, hundreds, thousands and then lakhs and crores. Commas are used to mark thousands, lakhs and crores. The first comma comes after hundreds place (three digits from the right) and marks thousands. The second comma comes two digits later (five digits from the right). It comes after ten thousands place and marks lakh. The third comma comes after another two digits (seven digits from the right). It comes after ten lakh place and marks crore.
Ex: 5, 08, 01, 592
3, 32, 40, 781
7, 27, 05, 062
Suppose a newspaper report states that Rs.2500 crore has been allotted by the government for National Highway construction. The same amount of Rs.2500 crore is sometimes expressed as Rs. 25 billion. In the Indian system, we express it as Rs. 2500 crore and in the International system, the same number is expressed as 25 billion. Hence we need to understand both the systems and their relationship.
Ascending order
Ascending order means arrangement from the smallest to the greatest.
Descending order
Descending order means arrangement from the greatest to the smallest.
Ex: Arrange the following numbers in ascending order :
257536, 38952, 385081, 365062
Sol. The smallest number is 38952. Other numbers greater than 38952, in order are 257536, 365062 and 385081.
∴ The numbers in ascending order are 38952, 257536, 365062, 385081.
Ex: Arrange the following numbers in descending order : 19710, 887151, 453212, 925473
Sol. The greatest number is 925473. Other numbers smaller than 925473 in order are 887151, 453212 and 19710.
∴ The numbers in descending order are 925473, 887151, 453212, 19710.]
1. Numbers: Comparing, Shifting Digits, Revisiting Place Value and Large Numbers

We just looked at the number of digits and found the answer. The greatest number has the most thousands and the smallest is only in hundreds or in tens. Make five more problems of this kind and give them to your friends to solve. Now, how do we compare 4875 and 3542? This is also not very difficult. These two numbers have the same number of digits. They are both in thousands. But the digital the thousands place in 4875 is greater than that in 3542. Therefore, 4875 is greater than 3542. Next tell which is greater, 4875 or4542? Here too the numbers have the same number of digits. Further, the digits at the thousands place are the same in both. What do we do then? We move to the next digit, that is to the digit at the hundreds place. The digit at the hundreds place is greater in 4875 than in 4542. Therefore, 4875 is greater than 4542.
1. Numbers: Comparing, Shifting Digits, Revisiting Place Value and Large Numbers
- Books Name
- Mayank classes Mathematics Book
- Publication
- Mayank classes
- Course
- CBSE Class 6
- Subject
- Mathmatics
.90u9
1. Numbers: Comparing, Shifting Digits, Revisiting Place Value and Large Numbers
- Books Name
- MD AFZAL AHMAD Mathematics Book
- Publication
- MD AFZAL AHMAD
- Course
- CBSE Class 6
- Subject
- Mathmatics

Introduction:-
Counting Numbers: -The numbers which we can count. Like 1, 2, 3, 9, 37 etc.
Natural Numbers: -The numbers which we can count and it starts from 1 and goes on. Like 1, 2, 3, 4, …….100, …….2000, …………... etc.
Whole Numbers: -The counting numbers which starts from Zero are called whole numbers and goes on. Like 0, 1, 2, 3, 4, …….100, …….2000, …………... etc.
Integers: -Integers are the collection of whole numbers and negative numbers. Integers can be positive numbers, Zero and negative numbers but it cannot be a fraction. Like -229, -85, -16, -5, -1, 0, 1, 5, 29, 219, 5000 etc.
Even Numbers: -The numbers which are completely divisible by 2. It means those numbers which we divide by 2, remainder becomes Zero (0). Like 2, 4, 6, 22, 100, 294, 604 etc
Smallest Even number is 2.
Odd Numbers: - The numbers which are not completely divisible by 2. It means those numbers which we divide by 2, remainder becomes One (1). Like 1,3, 5, 7, 21, 101, 299, 1001 etc
Smallest Odd number is 1.
Composite Number: -A composite number is a natural number or positive integers which has more than two factors.
It means the given number is completely divisible by more than two numbers. Like 6, which is completely divisible by 1, 2, 3 and 6. It means 6 has four factors.
Example: - 4, 6, 8, 10, 12, 256 etc.
Smallest composite number is 4.It has three factors, these are 1,2, 4.
Prime Number: -A prime number is a natural number that is completely divisible by 1 and the number itself. Prime number has only two factors these are 1 and the number itself.
Like 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47 etc.
Smallest prime number is 2.
Twin Prime Number: -Two prime numbers are called twin prime, if there is present only one composite number between them.Like {3,5}, {5,7}, {11,13}, {17,19}, {29,31}, {41,43} etc. Two consecutive prime number can be twin primes.
{2,3} is not a twin prime number, because there is no composite number in between them.
Co-prime Number: -Two numbers are co-prime, if they have no common factor other than 1 or we can say that the HCF (Highest Common Factor) of these numbers is 1.Like {1,3}, {4,5}, {13,31}, {18, 35}, {15,17}, {29,30}.
It is not necessary that these numbers should be prime.
1. Numbers: Comparing, Shifting Digits, Revisiting Place Value and Large Numbers
- Books Name
- Class 6 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 6
- Subject
- Mathmatics
CHAPTER -1
KNOWING THE NUMBERS
Comparing Shifting Digits, Revisiting Place Value and Large Numbers
Numbers are compared to check which Number is Greater or smaller than the other number. There are different ways to know that a number is smaller or Greater.
These are:
If the numbers used in the question is different. The number having next number is smaller and the other number is Bigger.
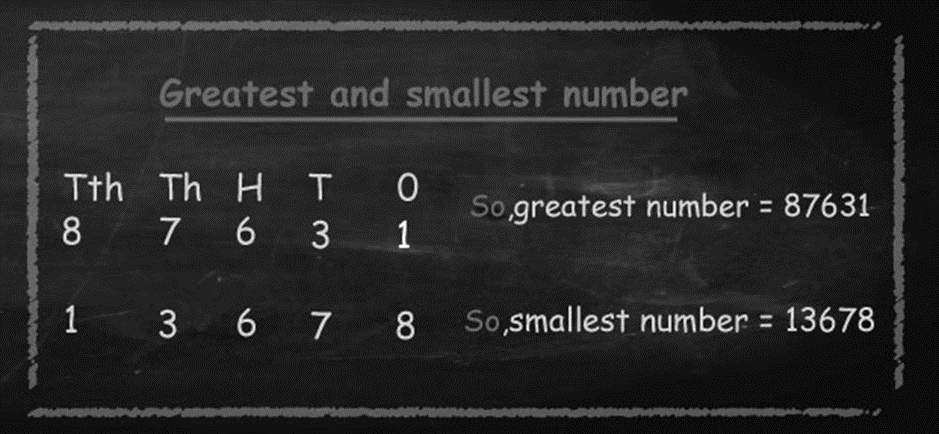
For Example: 1. Find out Greatest Number from 125 and 120.
Solution: 125 is bigger number and 120 is smaller Number. Hence the number 125 is greatest.
2. Find out greatest and smallest number from 320, 1340, 158, 228, 5446, and 4525
Solution: Here 5446 is the greatest and 158 is the smallest.
If the number of digits is equal than the number at the greatest place is compared.
If the integers at the greatest place are different, the greater value is larger number and the smaller value is the smaller number.
For Example: 1.Compare 285 and 685,
Solution: The numbers of integers are same, but number at greatest (then hundreds) place, is 2 and 6. Since 6 is greater number than 2, hence 685 is greater and 285 is smaller.
If the integers at the greatest place are equal, then another place is compared and so on.
For Example: 1. Compare 353 and 335.
Solution: The number of integers and number at greatest place are same then we will check the second greatest number place and compare both the numbers. Since 5 is advanced than 3. Therefore 353 is greater number and 335 is smaller number
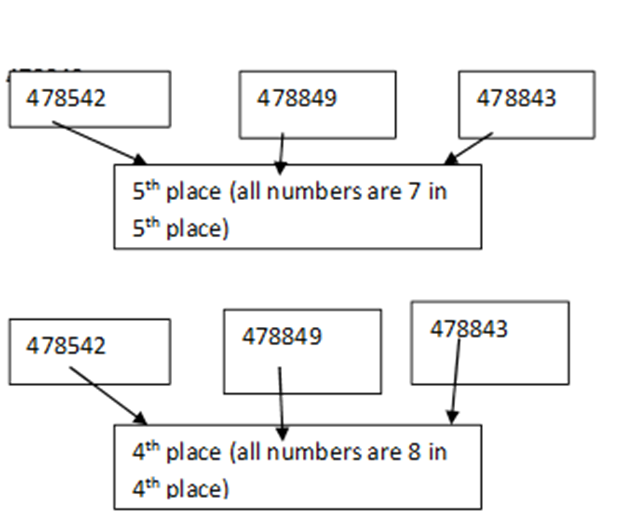
2. Compare among 478542, 478849 and 478843.
Solution: There are same number of integers and number at the greatest integers places are same for last three positions (4th place numbers are same for all the numbers), (5th place numbers are same for all the numbers) and (6th place numbers are same for all the numbers) and 2nd place is also same for all the numbers).3rd place number is same for
Second and third digit. So now we will compare first digit 3rd place number with another two numbers third place. Since 8 is bigger than 5.
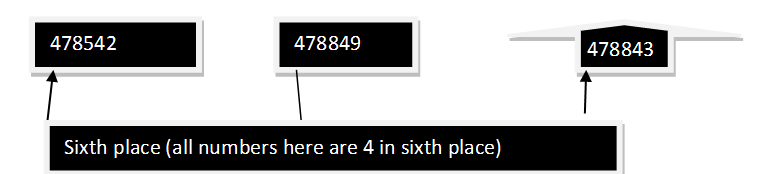

Numerals
One of the early systems of writing numbers is the system of Roman Numerals. This system is still used in different places. For Example, we can see the use of Roman Numerals in Clock. It's also used in classes for the School time table.
Roman Numerals are expressed by seven letters of the Alphabets.
Rules of the System
The Roman Numerals I, II, III, IV, V, VI, VII, VIII, IX, X denote number 1 to 10 . Then
XI for 11,
XII for 12 … till XX for 20.
VI = 5 +1 = 6,
XII = 10 +2 = 12 and
LXV = 50 +10 + 5 = 65
2. Large Numbers in Practice
- Books Name
- CBSE Mathematics for Class 6
- Publication
- Carrier Point
- Course
- CBSE Class 6
- Subject
- Mathmatics
sudhanshu@kaysonseducation.co.in
CBSE Mathematics for Class 6 > Chapter 1: Knowing Our Numbers > Roman Numerals
Notes Added through teacher account.
2. Large Numbers in Practice
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
ROMAN NUMERALS
One of the earliest systems of writing numerals is the Roman Numeral system. This system is still in use in many places. For example, some faces of clocks show hours in Roman numerals; we use Roman numerals to write numbered list; etc.
Unlike the Hindu-Arabic numeral system, Roman numeral system uses seven basic symbols to represent different numbers. The symbols are as follows :
The Roman numerals :
I, II, III, IV, V, VI, VII, VIII, IX, X denote 1,2,3,4,5,6,7,8,9 and 10 respectively. This is followed by XI for 11, XII for 12,... till XX for 20. Some more Roman numerals are :
I V X L C D M
1 5 10 50 100 500 1000
The rules for the system are :
(a) If a symbol is repeated, its value is added as many times as it occurs: i.e. II is equal 2, XX is 20 and XXX is 30.
(b) A symbol is not repeated more than three times. But the symbols V, L and D are never repeated.
(c) If a symbol of smaller value is written to the right of a symbol of greater value, its value gets added to the value of greater symbol.
VI = 5 + 1 = 6, XII = 10 + 2 = 12 and LXV = 50 + 10 + 5 = 65
(d) If a symbol of smaller value is written to the left of a symbol of greater value, its value is subtracted from the value of the greater symbol.
IV = 5 – 1 = 4, IX = 10 – 1 = 9
XL = 50 – 10 = 40, XC = 100 – 10 = 90
(e) The symbols V, L and D are never written to the left of a symbol of greater value, i.e. V, L and D are never subtracted.
The symbol I can be subtracted from V and X only.
The symbol X can be subtracted from L, M and C only.
Following these rules we get,
1 = I 10 = X 100 = C
2 = II 20 = XX
3 = III 30 = XXX
4 = IV 40 = XL
5 = V 50 = L
6 = VI 60 = LX
7 = VII 70 = LXX
8 = VIII 80 = LXXX
9 = IX 90 = XC
Ex : Write in Roman Numerals
(i) 69 (ii) 98.
Sol: (i) 69 = 60 + 9 = (50 + 10) + 9 = LX + IX = LX IX
(ii) 98 = 90 + 8 = (100 – 10) + 8 = XC + VIII = XCVIII
2. Large Numbers in Practice
- Books Name
- MD AFZAL AHMAD Mathematics Book
- Publication
- MD AFZAL AHMAD
- Course
- CBSE Class 6
- Subject
- Mathmatics
Roman Numbers
Roman Numbers are one of the earlier system of writing numbers. Like I, II, III, IV, V etc.
The Roman Numerals:
I, II, III, IV, V, VI, VII, VIII, IX, X These Roman numbers denote 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 respectively.
Some more Roman Numbers

Rules for the Roman Number System:
1) If a symbol is repeated, its value is added as many times as it occurs.
Like, II is equal to 2, III is 3, XX is 20, XXX is 30, CC is 200, MM is 2000, MMM is 3000 etc.
2) A symbol is not repeated more than three times. But the symbol V, L, D are never repeated.
3) If a symbol of smaller value is written to the right side of a symbol of greater value, its value gets added to the value of greater symbol. Like,
VI = 5+1 =6 VII= 5+2= 7 XIII= 10+3= 13 LXV= 50+10+5= 65CLX= 100+50+10=160
4) If a symbol of smaller value is written to the left of the symbol of greater value, its value is subtracted from the value of greater symbol.
IV = 5-1= 4 IX= 10-1= 5 XL= 50-10= 40 XC= 100-10= 90 CD= 500-100= 400
5) The symbols V, L and D are never written to the left of a symbol of greater value, i.e. V, L and D are never subtracted.
The Symbol I can be subtracted from V and X only.
The symbol X can be subtracted from L, M and C only.
Roman Numbers using these rules

Some Solved Examples.

5) 1236 = 1000 + 200 + 30 + 6
Roman number for 1000 = M
Roman number for 200 = CC
Roman number for 30 = XXX
Roman number for 6 = VI
So, Roman number for 1236= MCCXXXVI
2. Large Numbers in Practice
- Books Name
- Class 6 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 6
- Subject
- Mathmatics
Large Numbers in Practice
Large Numbers can be shown using the place value. It goes in the thrusting order as shown below
8 integers 7 integers 6 integers 5 integers 4 integers 3 integers
centimeter( cm) in used as a unit of dimension of length. We can use this unit for measuring the length of a pen, the range of a book or note booket. but this unit is too big to measure the consistence of a pen. So, we use another unit named as millimeter( mm). Also, centimeter and millimeter are veritably small units to measure the length of the wall or a room. We use another unit named as meter for the same. Indeed meter is too small unit when we state the distances between two municipalities or metropolises. For this we need kilometers( km).
The relations between units are
1 kilometer = 1000 meters( m)
1 meter = 100 centimeters( cm)
1 centimeter = 10 millimeters( mm)
Also, we have
100 cm = 1 m = 10mm × 100 = 1000 mm
1000 m = 1Km = 1000 × 100 cm = 100000 cm
100000 cm =1 km = 100000 × 10 mm = 1000000 mm
10 Million = 1 crore
1 million = 10 lakhs
(100,000) Hundred Thousands = 1 lakh
(10,000)Ten Thousands = Thousands Hundreds (1000,000)
We borrow the following rules to compare two large figures
Rule- 1 The number with further integers is lesser than the number with lower integers.
Rule- 2 When two figures have the same number of integers, compare the integers at the leftmost places. The number with the lesser number is lesser. If the integers at the leftmost places are the same also compare the coming integers and so on.
3. Estimation of Numbers
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
USING BRACKETS
Meera bought 6 notebooks from the market and the cost was Rs 10 per notebook. Her sister Seema also bought 7 notebooks of the same type. Find the total money they paid.
Seema calculated the
6 × 10 + 7 × 10 = 60 + 70 = 130
Meera calculated the amount like this amount like this
6 + 7 =13 and 13 × 10 = 130
Ans. Rs 130.
We can see that Seema’s and Meera’s ways to get the answer are a bit different.
To avoid confusion in such cases we may use brackets. We can pack the numbers 6 and 7 together using a bracket, indicating that the pack is to be treated as a single number.
Thus, the answer is found by (6 + 7) × 10 = 13 × 10.
First, turn everything inside the brackets ( ) into a single number and then do the operation outside which in this case is to multiply by 10.
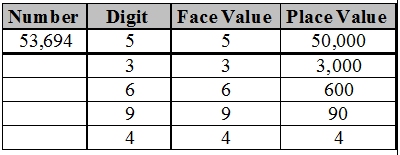
FACE VALUE
Face value of a digit in a numeral is the value of the digit itself at whatever place it may be.
PLACE VALUE
Place value of a digit in a given number is the value of the digit because of the place or the position of the digit in the number.
Place value of a digit = Face value of the digit × value of the place
Place value and Face value :
Every digit has two values – the place value and the face value. The face value of a digit does not change while its place value changes according to its position and number.
Expanded form of a Number :
If we express a given number as the sum of its place value, it is called its expanded form.
Ex: Express
(i) 3,64,029 (ii) 2,75,00,386 in expanded form.
Sol. Place value of 3 = 3 x 100000
Place value of 6 = 6 x 10000
Place value of 4 = 4 x 1000
Place value of 0 = 0 x 100
Place value of 2 = 2 x 10
Place value of 9 = 9 x 1
∴ The expanded form of 3,64,029 is
3 x 100000 + 6 x 10000 + 4 x 1000 + 0 x 100 + 2 x 10 + 9 x 1.
3. Estimation of Numbers
Look and Guess the Number
3. Estimation of Numbers
- Books Name
- Class 6 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 6
- Subject
- Mathmatics
Estimation
The estimation of a number is a reasonable approximation of the real value. Estimation means approaching an amount to the closeness needed. This is done by rounding off the figures involved and getting a quick and rough answer.

Rounding off a number to the nearest tens numbers
The numbers 1, 2, 3, 4 are nearest to 0. So, these numbers are rounded off to smaller ten. The numbers 6, 7, 8, 9 are nearest to 10. So, these numbers are rounded off to the bigger tens. The number 5 is nearest from both 0 and 10, so it's rounded off to the advanced ten.
e.g.
(i) We round off 41 to the nearest ten as 40
(ii) We round off 67 to the nearest ten as 70
(iii) We round off 55 to the nearest ten as 60
Rounding off a number to the nearest hundreds number
The numbers 201 to 249 are closer to 200. So, these numbers are rounded off to the nearest hundred i.e. 200. The numbers 251 to 299 are closer to 300. So, these numbers are rounded off to the advanced hundred i.e. 300. The number 250 is rounded off to the advanced hundred.
(i) We round off 678 to the nearest 100 as 700.
(ii) We round off 510 to the nearest 100 as 500.
Rounding off a number to the nearest thousands number
Also, 1001 to 1499 are rounded off to the lower thousand i.e. 1000, and 1501 to 1999 to the advanced thousand i.e. 2000. The number 1500 is equidistant from both 0 and 1000, and so it's rounded off to the advanced thousand i.e. 2000.
(i) We round off 3574 to the nearest thousand as 4000.
(ii) We round off 8105 to the nearest thousand as 8000.
Estimation of sum or difference
When we estimate sum or difference, we should have an idea of the place to which the rounding is demanded.
e.g.
(i) Estimate 5798 + 29834
We can say that 29834 > 5798
We shall round off the figures to the nearest thousands.
29416 is rounded off to 30000
5679 is rounded off to 6000
Estimated sum
49000 + 3000 = 52000
(ii) Estimate 2476 – 946
We shall round off these figures to the nearest hundreds.
2476 is rounded off to 2000
946 is rounded off to 1000
Estimated difference
2000 – 1000 = 1000
Estimation of the product
To estimate the product, round off each factor to its topmost place, also multiply the rounded off factors.
Estimate 82 x 578
The first number, 82, can be rounded off to the nearest ten as 80.
The alternate number, 678, can be rounded off to the nearest hundred as 700.
Hence, the estimated product = 80 x 700 = 56000.
Using Brackets
Brackets help in simplifying an expression that has multiple operations. If any statement that includes the brackets is there, then perform the operation inside the bracket first and simplify each number in to a single number. Then carry out the operation that is outside the bracket.
e.g.
1. (6 8) x 10 = 14 x 10 = 140
2. (8 3) (9-4) = 11 x 5 = 55
Expanding Brackets
The use of classes allows us to follow a certain procedure to expand the classes totally.
E.g.
8 x 109 = 8 x (100 9) = 8 x 100 8 x 9 = 800 72 = 872
105 x 108 = (100 +5) x (100 + 8)
= (100+ 5) x 100 (100 + 5) x 8
= (100 x 100) (5 x 100) (100 x 8) (5 x 8)
= 10000 500 800 40
= 11340.
Brackets are used to reduce the confusion while solving the questions like add, subs tract, multiply and divide. For solving a bracket statement, first estimate and make a single number in the bracket and also estimate the outside part.
Problem:
(3+ 4) x 5 = (7) x 5 = 7 x 5 = 35
This shouldn't be calculated as (3 4) x 5 = (3) 4x5.
Classes are expanded to estimate individual integers inside the classes with the integers outdoors.
(3+ 4) x 5 = 3 x 5 4 x 5 = 15 20 = 35
Problem: Write the expressions for each of the following using classes.
Expression using words
Expression using Figures and classes
The number six is multiplied by the sum of seven and three
6 x (7 +3) OR (7 +3) x 6
Divide the subtraction of eighteen and six by four
(18-6)/ 4
Divide eighty five by four times the sum of five and four
85/ ((4 +5) x 4)

Large Numbers in Practice
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics

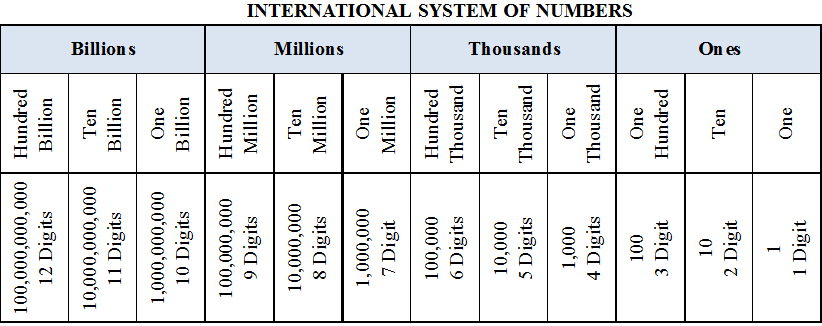
Large Numbers in Practice
we have learnt that we use centimetre (cm) as a unit of length. For measuring the length of a pencil, the width of a book or notebooks etc., we use centimetres. Our ruler has marks on each centimetre. For measuring the thickness of a pencil, however, we find centimetre too big. We use millimetre (mm) to show the thickness of a pencil.
(a) 10 millimetres = 1 centimetre
To measure the length of the classroom or the school building, we shall find centimetre too small. We use metre for the purpose.
(b) 1 metre = 100 centimetres = 1000 millimetres
Even metre is too small, when we have to state distances between cities, say, Delhi and Mumbai, or Chennai and Kolkata. For this we need kilometres (km).
We have done a lot of problems that have addition, subtraction, multiplication and division.
We will try solving some more here.
Ex : Population of Sundarnagar was 2,35,471 in the year 1991. In the year 2001 it was found to be increased by 72,958. What was the population of the city in 2001?
Sol. Population of the city in 2001 = Population of the city in 1991 + Increase in population
= 2,35,471 + 72,958
Now, 235471
+ 72958
308429
Salma added them by writing 235471 as 200000 + 35000 + 471 and 72958 as 72000 + 958.
She got the addition as 200000 + 107000 + 1429 = 308429.
Mary added it as 200000 + 35000 + 400 + 71 + 72000 + 900 + 58 = 308429
Answer : Population of the city in 2001 was 3,08,429.
All three methods are correct.
Ex: In one state, the number of bicycles sold in the year 2002-2003 was 7,43,000. In the year 2003-2004, the number of bicycles sold was 8,00,100. In which year were more bicycles sold? and how many more?
Sol. Clearly, 8,00,100 is more than 7,43,000. So, in that state, more bicycles were sold in the year 2003-2004 than in 2002-2003.
Now, 800100
– 743000
057100
Check the answer by adding
743000
+ 57100
800100 (the answer is right).
Answer : 57,100 more bicycles were sold in the year 2003-2004.
Comparing Numbers
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Comparing Numbers
Take two numbers. The number with greater number of digits is greater. However, if the two numbers have the same number of digits, then the number which has a larger left most digits is larger. If this digit also happens to be the same, then we proceed to next digit and use the same criterion and so on.
Ex: Which is greater of 270346 and 48356?
Sol. 270346 has 6 digits
48356 has 5 digits
6 digits are more than 5 digits
∴ 270346 is greater than 48356
or 270346 > 48356
Greater number has more number of digits.
Ex: Find the greatest and the smallest numbers from the following group of numbers :
23787,6895, 24569, 24659
Sol. Greatest number : 24659
Smallest number : 6895.
(i) Making number without repetition of digits : In case of non-repetition of digits, it is better if we start making the number from left.
Ex: Write the greatest and the smallest 5-digit numbers by using each of the digits 8, 4, 7, 0, 2 only once.
Sol. For the greatest number, we write the greatest digit 8 in the T-thousands column. Next smaller digit in the thousands column and so on.
∴ The greatest number = 87420.

For the smallest number, we write the smallest digit in the T-thousands column. But here 0 is the smallest digit. 0 is not written on the extreme left of a number. So, we write 2 in the T-thousands column and 0 in the thousands column. Next digit greater than 2 is written in the hundreds column and so on.
∴ The smallest number = 20478

(ii) Making number with repetition of digits : In case of repetition of digit, it is better if we start making number from right.
Ex: Write the greatest and smallest numbers of 4 digits using all the digits 8,0, 5.
Sol For greatest number, select the smallest digit 0 and write in the ones column. Next greater digit is written in the tens column. Next greater digits 8 is written in the hundreds column. Since no digit greater than 8 given, so we repeat 8 in the thousands column.
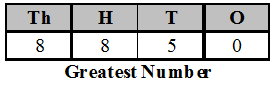
∴ The greatest number = 8850
For smallest number, select the greatest digit 8 and write in the ones column. Next smaller digit in tens column and so on. Repeat the smallest digit in the end. But here 5 is smaller than 8 and then comes 0 which cannot be repeated in the end.
So, we write 5 in the end and repeat 0 in the tens place.
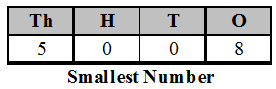
∴ The smallest number = 5008.
ESTIMATION IN NUMBER OPERATION
410 is closer to 400, so it is rounded off to 400, correct to the nearest hundred.
889 lies between 800 and 900.
It is nearer to 900, so it is rounded off as 900 correct to nearest hundred.
Numbers 1 to 49 are closer to 0 than to 100, and so are rounded off to 0.
Numbers 51 to 99 are closer to 100 than to 0, and so are rounded off to 100.
Number 50 is equidistant from 0 and 100 both. It is a common practice to round it off as 100.
(i) Estimating (Rounding) to the Nearest Ten : To round off a number to the nearest ten consider the ones digit. If the ones digit is 5 or greater than 5, then change the ten’s digit to the next higher digit and ones digit to zero. If the ones digit is less than 5, then leave the tens digit unchanged but change the ones digit to zero.
(ii) Estimating (Rounding) to the Nearest Hundred : To round off a number to the nearest hundred, consider the tens digit. If the ten’s digit is 5 or greater than 5, then change the hundreds digit to the next higher digit and tens, ones digits to zeros. If the tens digit is less than 5, then leave the hundreds digit unchanged but change the tens and ones digits to zeros.
(iii) Estimating (Rounding) to the nearest Thousand : To round off a number to the nearest thousand, consider the hundreds digit. If this digit is 5 or greater than 5, then change the thousands digit to the next higher digit and change all the other digits before that to zeros. If the hundreds digit is less than 5, then leave the thousands digit unchanged but change all the other digits before that to zeros.
Ex : Estimate: 5,290 + 17,986.
Sol.: You find 17,986 > 5,290.
Round off to thousands.
17,986 is rounds off to 18,000
+5,290 is rounds off to + 5,000
Estimated sum = 23,000.
Ex : Estimate: 5,673 – 436.
Sol.: 5,673 rounds off to 5,700
– 436 rounds off to – 400
Estimated difference = 5,300.
Ex : Estimate the following products :
(i) 87 × 313 (ii) 9 × 795 (iii) 898 × 785
Sol. (i) 87 is rounded off to 90
313 is rounded off to 300
∴ Estimated product = 90 × 300 = 27000
(ii) 9 is not rounded off [ ∴ it is a one-digit no.
795 is rounded off to 800
∴ Estimated product = 9 × 800 = 7200
(iii) 898 is rounded off to 900
785 is rounded off to 800
∴ Estimated product = 900 × 800 = 720000.
(iv) Estimation in Quotients : In the process of estimation in quotients, we round off the dividend and the divisor before the process of division.
Ex: Estimate the following quotients :
(a) 81 ÷ 17 (b) 7525 ÷ 365
Sol. (a) 81 is rounded to 80
17 is rounded to 20
To get the estimated quotient think of dividing 80 by 20 or 8 by 2.
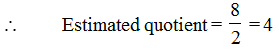
(b) 7525 is rounded to 8000
365 is rounded to 400
To get the estimated quotient think of dividing 80 by 4.
∴ Estimated quotient = 20.
Comparing Numbers
Comparing numbers
Numbers are compared to check which one is higher/smaller than the others. Following things are checked to know that a number is greater or smaller:
If the number of digits in the numbers are different. The number having more digits is greater and the other is smaller.
- For example, among the two numbers 324 and 22, 324 is higher as it has more number of digits. 22 has lower number of digits, hence it is smaller.
- For example, among 221, 34, 1356, 222, 45225, 45225 is the highest and 34 is the lowest.
If the number of digits is equal then the digit at the highestplace is compared.
- If the digits at the highest place are different, the higher value is larger number and the lower value is the smaller number.
- For example, among 235 and 643, the number of digits are same but digit at highest (here hundreds) place, is 2 and 6. Since 6 is higher than 2, hence 643 is higher and 235 is smaller.
- If the digits at the highest place are equal, then the next higher place is compared and so on.
- For example, among 235 and 245, the number of digits and digit at highest place are same so digit at 2nd highest (tens) place is compared. Since 4 is higher than 3, hence 245 is higher and 235 is smaller.
- For example, among 267542, 267894 and 267843, the number of digits and digits at 4 highest places are same (for 2nd and 3rd number) so digit at 5th highest place is compared. Since 9 is higher than 4, hence 267894 is higher than 267843 and 267542.
Comparing Numbers
- Books Name
- MD AFZAL AHMAD Mathematics Book
- Publication
- MD AFZAL AHMAD
- Course
- CBSE Class 6
- Subject
- Mathmatics
Comparing Numbers
How to compare numbers:
We do compare numbers by seeing which number is larger or which one is smaller.
Let we have numbers like 7,1, 3, 9, 5.
By seeing we can say, here 1 is the smallest number and 9 is the largest number.
Examples:
Rules to compare numbers
1. Count the number of digits. Number with more digits is greater.

How many numbers can we make from given number of digitswithout repeatation of digits.
Let we have four digits, like 5, 3, 4, 6. We want to make four different numbers using these digits without any repeatation.
These four numbers are 3,456, 4,356, 5,346 , 6,543
Here, Smallest number is 3,456 and largest number is 6,543.
Arranging Numbers.
Ascending Order:-Arrangement of numbers from smallest to greatest
Example:- 17<19<35<102
Descending Order:-Arrangement of numbers from greatest to smallest
Example:- 102> 35>19>17

 Success Academy
Success Academy
 Carrier Point
Carrier Point
 ReginaTagebücher
ReginaTagebücher
