2. Divisibility Rule

Some problems on HCF and LCM
 Ex.     Find the greatest number which divides 43 and 91 leaving remainder 7 in each caes.
 Sol.     It is given that the required number when divides 43 and 91, the renainder is 7 in each case . This means that 43 – 7 = 36  and 91– 7  = 84   are completely divisible by required number . 
Also, the required number is the greatest number satisfying the above property .
       ∴      It is the HCF of 36 and 84.
            36 = 2 × 2 × 3 × 3 
            84 = 2 × 2 × 3 × 7 
       ∴    Required HCF = 2 × 2 × 3 = 12
        Hence, the required number  = 12

Ex.     Find the largest number that will divide 20, 57 and 85 leaving remainders 2, 3 and 4 respecitively.
Sol.   Clearly, the required number is the HCF of the number 20 – 2 = 18, 57 – 3 = 54 and 85 – 4 = 81.  
        18 = 2 × 3 × 3  
        54 = 2 × 3 × 3 × 3 
        81 = 3 × 3 × 3 × 3 
        ∴   Required HCF = 3 × 3 = 9
        Hence, the required number  = 9

Relationship between HCF and LCM 
Let us take two numbers, say 16 and 24.
The HCFof 16 and 24 is 8.
The LCM of 16 and 24 is 48.
Since 8 is factor of 48, so we can say that HCF of the numbers is a factor of their  LCM.
Product of HCF and LCM = 8 × 48 = 384
Product of Numbers = 16 x 24 = 384
So we can say that the product of two numbers is equal to the product of  their HCF and LCM.
Let a and b are two numbers then

a x b =  HCF × LCM 

Ex.     The HCF of two number is 29 and their LCM is 1160. If one of the number is 145,  find the other.
Sol.     We know that 
        Product of the number      = HCF × LCM
                x × 145 = 29 × 1160
                         
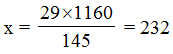
        ∴    Required number  = 232

Ex.     Find the least number which when divided by 6, 7, 8, 9 and 10 leaves reamainder 1.
Sol.     As the remainder is same
        Required number = LCM of divisors + Remainder
                                    = LCM (6, 7, 8, 9, 10) +1
                                    = 2520 + 1 = 2521

Ex.    Find the least number which when decreased by 7 is exactly divisible by 12, 16, 18, 21 and 28.
   
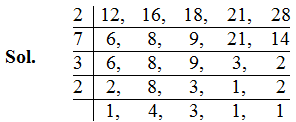
        LCM = 2 × 7 × 3 × 2 × 4 × 3 = 1008
        Required number = 1008 + 7 = 1015. 

Tests for divisibility of Numbers

Divisibility rule of 2 and 4?
We can tell if 2 divides into this number without a remainder by just looking at the last number-the last number is a 4.

This means that the number is Even and 2 will divide into it without a remainder is divided by 2.
The Rule for 2 any whole number that ends in 0, 2, 4, 6, or 8 will be divided by 2.
A number is divided by 3 if the sum of the integers of the number is divided by 3.
The Rule for 4 if the last two integers of a whole number are divided by 4, also the entire number is divided by 4.

Tests for divisibility of numbers 5- 8,
The Rule for 5 Number that are divided by 5 must end in 5 or 0.
A number is divided by 6 if the number is divided by both 2 and 3.
A number is divided by 7 if the given number is divided by 7
The Rule for 8 if the last three integers of a whole number are divided by 8, also the entire number is divided by 8

Tests for divisibility of numbers 9- 11
A number is divided by 9 if the sum of the integers is divided by 9.
The Rule for 10 numbers that are divided by 10 need to be even and divided by 5, because the prime factors of 10 are 5 and 2. Primarily, this means that for a number to be divided by 10, the last number must be a 0.
A number is divided by 11 if the sum of the integers is divided by 11.

Some results on divisibility rule