- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Lowest Common Multiple
The Lowest Common Multiple (LCM) of two or more given numbers is the lowest (or smallest or least) of their common multiples.
Ex.: Find the LCM of 24 and 90.
Sol.: The prime factorisations of 24 and 90 are:
24 = 2 × 2 × 2 × 3; 90 = 2 × 3 × 3 × 5
In these prime factorisations the maximum number of times the prime factor 2 occurs is three; this happens for 24. Similarly, the maximum number of times the prime factor 3 occurs is two; this happens for 90. The prime factor 5 occurs only once in 90.
Thus, LCM = (2 × 2 × 2) × (3 × 3) × 5 = 360
- Books Name
- Class 6 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 6
- Subject
- Mathmatics
Common factors and common multiples
What are Multiples?
Multiple is a result attained by multiplying a number by an integer (it should not be a bit). By taking out the product of the counting numbers and that of whole numbers the multiples of the whole number are attained. For illustration, if we
multiply number 6 by 1,number 6 by 2, number 6 by 3, and so on then we can find the multiples of number 6,
The multiples are the product of this addition. Every multiple of a number is lower than or equal to that number.
The number of multiples of given number is infinite
Common Multiple: common multiples of numbers are the
Multiple of numbers that are common to two numbers .
Common Factors: Factors that are common to two or more numbers are known as their common factors.
Factors of 30 and 45 are –
30 = {1, 2, 3, 5, 10, 15, and 30}
45 = {1, 3, 5, 9, 15, 45}
1, 3, 5 and 15 are the Common factors of 30 and 45.
For illustration, the factors of 20 are 1, 2, 4, 5, 10, and 20.
For illustration, the multiples of 20 are 20, 40, 60, 80, 100, etc.
- Some more divisibility rules
If the number of integers of a number is even, also add the first number and subtract the last number from the rest of the number.
Example 3784
Number of integers = 4
Now, 78 3 – 4 = 77 = 7 × 11
Therefore, 3784 is subtract by 11
If the number of integers of a number is odd, also subtract the first and the last integers from the rest of the number.
Illustration 82907
Number of integers = 5
Now, 275 × 11 = 290 – 8 – 7
Therefore, 82907 are subtracting by 11.
Form the groups of two integers from the right end number to the left end of the number and add the even groups. However, also the number is subtracting by 11, if the sum is a multiple of 11.
Example 3774 = 37 74 = 111 = 1 11 = 12
3774 isn't subtracted by 11.
253 = 2 53 = 55 = 5 × 11
253 is subtracting by 11.
Subtract the last number of the number from the rest of the number. However, also the original number will be subtracting by 11, if the attendant value is a multiple of 11.
Example 9647
964 – 7 = 957 = 9647
95 – 7 = 88 = 8 × 11 =957 =
Therefore, 9647 is subtracted by 11.
Divisibility Rule of 12
Still, also the number is subtracting by 12 exactly, If the number is subtract by both 3 and 4.
Illustration 5864
Sum of the integers = 5 8 6 4 = 23 (not a multiple of 3)
Last two integers = 64(subtract by 4)
The given number 5846 is subtracting by 4 but not by 3; hence, it isn't subtract by 12.
Divisibility Rules for 13
For any given number, to check if it's subtract by 13, we've to add four times of the last number of the number to the remaining number and repeat the process until you get a two-number number. Now check if that two-number number is subtracting by 13 or not. However, also the given number is subtracting by 13, if it's subtract.
For illustration 2795 → 279(5 x 4)
→ 279(20)
→ 299
→ 29(9 x 4)
→ 29 36
→ 65
Number 65 is subtracting by 13, 13 x 5 = 65.
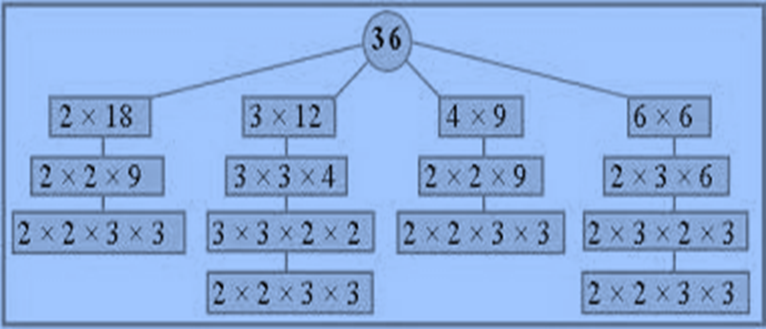
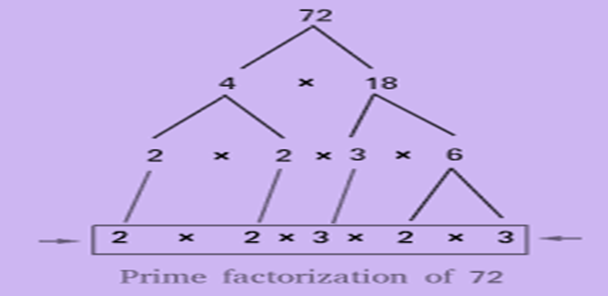
Prime Factorisation
Prime factorization is to write a composite whole number as the product of prime numbers only.
Highest common factor
HCF) of two or more given Numbers is the Highest (or topmost) of their common factors. It's also known as Greatest Common Divisor (GCD).
The topmost common factor of given numbers is called H.C.F.
To find the HCF of two or more Numbers, we can use any of the given system.
1. Common factor system
2. Prime factorization system
Lowest Common Multiple
The smallest common multiple of given numbers is called L.C.M.
L.C.M. of two or more high numbers is equal to their addition.
L.C.M. of two or more high numbers is equal to 1.
Every numbers have the smallest common factor number is always 1.

Problems on HCF and LCM


 Param Publication
Param Publication
 ReginaTagebücher
ReginaTagebücher
