2. Area of Rectangle and Regular Shapes

Perimeter
    The perimeter of a closed figure is the length of the boundary of the figure.
    The idea of perimeter is widely used in our daily life.

•          A farmer who wants to fence his field.
•          An engineer who plans to build a compound wall on all sides of a house.
•          A person preparing a track to conduct sports.

    All these people use the idea of ‘perimeter’.

1.    Perimeter of Rectangle:  The perimeter of a rectangle is the sum of all its sides. The opposite sides of rectangle are equal. If one side is l unit and the other side is b unit, then 

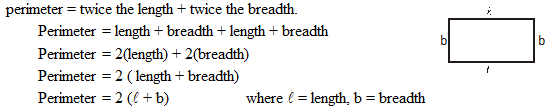
2 .    Perimeter of a square: All four sides of a square are equal. If one side of a square measures 'a' unit, we can say that both the length and the breadth are a unit each.    

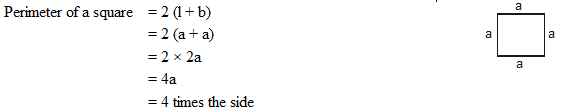
     The perimeter of a square is equal to four times the length of its sides.

3.    Perimeter of a triangle :

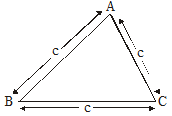
Perimeter = AB + BC + CA = a + b + c

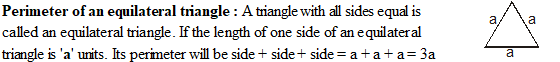
Note: In general, if the sides of a polygon are equal, that is, if it is a regular polygon, its perimeter will be the product of the length of its side with the number of sides.
        The perimeter of a regular pentagon = 5a units 
        The perimeter of a regular hexagon = 6a units
        The perimeter of a regular octagon = 8a units 
        where a is the length of one side.

Ex.1     Pinky runs around a square field of side 75 m, Bob runs around a rectangular field with a length of 160 m and breadth of 105 m. Who covers more distance and by how much?

Sol.:     Distance covered by Pinky in one round = Perimeter of the square 
                              = 4 × length of a side
                              = 4 × 75 m = 300 m
        Distance covered by Bob in one round     = Perimeter of the rectangle
                        = 2 × (length + breadth)
                        = 2 × (160 m + 105 m)
                        = 2 × 265 m = 530 m
        Difference in the distance covered = 530 m – 300 m = 230 m.
        Therefore, Bob covers more distance by 230 m.

Ex.2    Find the perimeter of a regular pentagon with each side measuring 3 cm.
Sol.:     This regular closed figure has 5 sides, each with a length of 3 cm.
        Thus, we get 
        Perimeter of the regular pentagon = 5 × 3 cm = 15 cm

Ex.3     A piece of string is 48 cm long. What will be the lenght of each side if the string is used to form:
        (i) a square             (ii) an equilateral triangle      (iii) an regular octagon .
Sol.  (i)     one side of  the square  = Perimeter ¸ 4 = 48 ¸ 4  = 12 cm      
        (ii)     one side of  the equilateral triangle  = Perimeter ¸  3 = 48 ¸ 3  = 16 cm      
        (iii)     one side of regular octagon = Perimeter ¸ 8 = 48 ¸ 8  = 6 cm  

 

Area of Rectangle and Regular Shapes

Introduction to area,

The area of any shape is the number of unit squares that can fit in to it.The area can be defined as the amount of space covered by a flat exterior of a particular shape. It is measured in terms of the" number of" square units (square centimetres, square height, square bases, etc.)

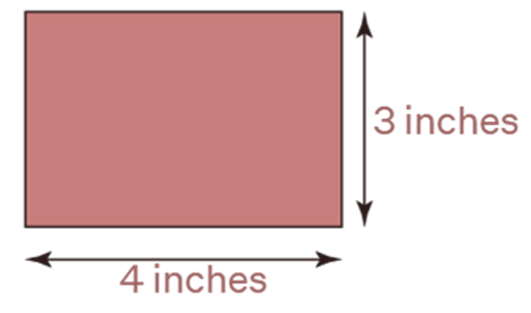
 Area of the rectangle,

Description Area of rectangle is the number of unit squares within the boundary of the rectangle. Alternately, the space caught up within the border of a rectangle is called the area of the rectangle. One good illustration of a rectangle shape is the lines of unit length in your house. You can freely figure out how important space the bottom occupies by counting the number of penstocks. This will also help you determine the area of the cubic floor.region involved by a rectangle within its four sides or boundaries.

 A = lb

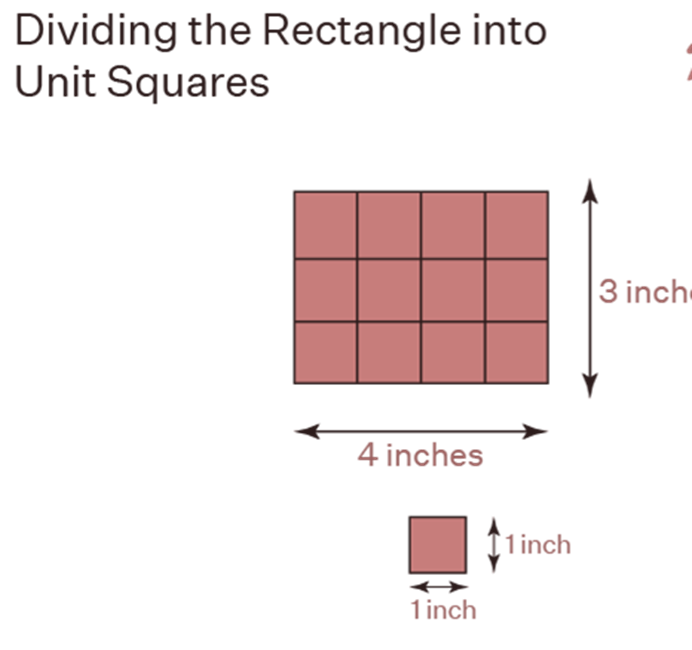
 How to Calculate the Area of a Rectangle

 Follow the way below to find the area

Step 1 Note the range of length and breadth from the given data

Step 2 Multiply length and breadth values

Step 3 Write the answer in square units

 Area of the square,

Area of a square is defined as the number of square units required to fill a square. In general, the area is defined as the region involved inside the boundary of a flat object or 2d figure. The dimension is done in square units with the standard unit being square measures (m2).
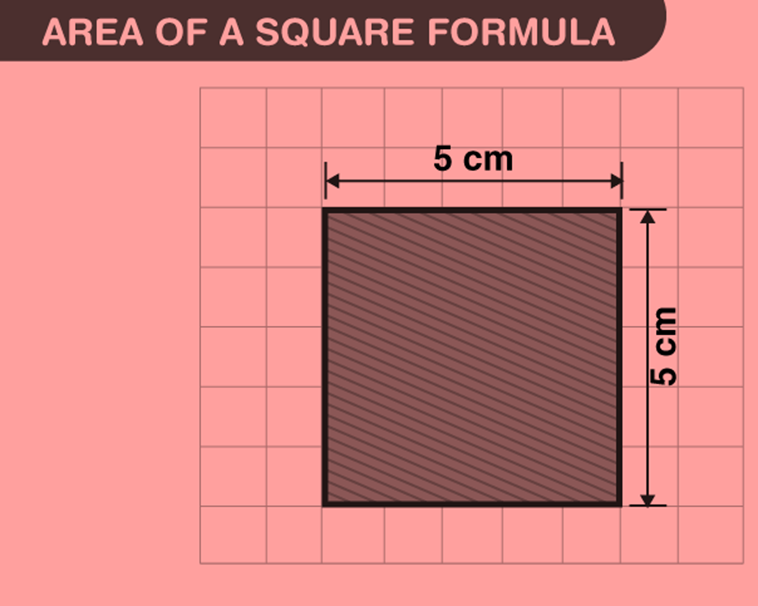
The area of square formula used for calculating the region involved, let us try using graph paper. You are needed to find the area of a side 5 cm. Using this dimension, draw a square on a graph paper having 1 cm × 1 cm squares. The square covers 25 complete squares.
Therefore, the area of the square is 25 square cm, which can be written as 5 cm × 5 cm, that is, side × side.
From the above discussion, it can be inferred that the formula can give the area of a square is
Area of a Square = Side × Side
Thus, the area of square = Side2 square units
And the perimeter of a square = 4 × side units

To find the area by counting the squares in the graph

The area of 1 full square can be taken as 1sq. unit.
Still, then the area can be considered as 1sq, if the region covers another than half the square. Unit.
Still, besides that region is neglected, if the region covers smaller than half the square.
Yet, also, the area is taken as 12sq, if the region covers exactly half the square. Unit.
These conventions are required to have in mind while chancing the area of the shape from the graph.
Sample
Find the area of the given shape by counting the squares.

 Answer

Let us count the number of squares.
Number of completely- filled squares = 6
Area of completely- filled squares = 6 × 1 = 6sq. cm
Number of half- filled squares = 2
 Area of half- filled squares = 2 × 12 = 1sq. cm
Number of further than half- filled squares = 4
 Area of other than half- filled squares = 4 × 1 = 4sq. cm
Number of lesser than half- filled squares = 2
 Area of smaller than half- filled squares can be neglected.
Total area covered by the given shape = (6 1 4) cm = 11sq. cm
Therefore, the total area covered by the given shape is 11sq. cm.