- Books Name
- CBSE Mathematics for Class 6
- Publication
- Carrier Point
- Course
- CBSE Class 6
- Subject
- Mathmatics
Notes adding
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Introduction
In this chapter we study the regions and boundrys of sum plain figures. We need some measures to compare them. We look into these now.
- Books Name
- Class 6 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 6
- Subject
- Mathmatics
Chapter 10
Mensuration
Perimeter of Rectangle and Regular Shapes
Introduction to perimeter,
Any shape that lies on a flat exterior and has only two extent i.e. length and breadth are called 2- D (two- dimensional) shape.
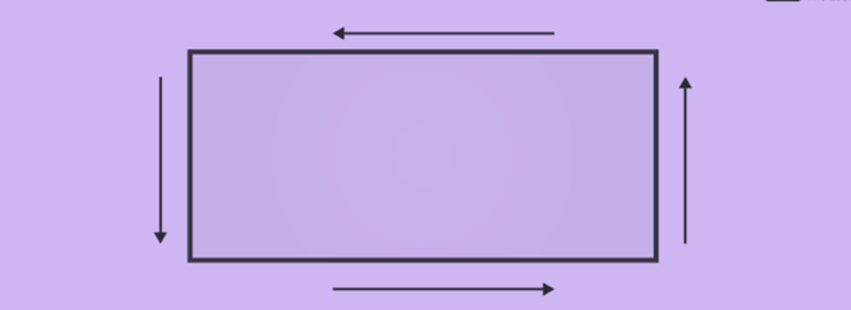
Polygons are closed numbers which are bounded by a chain of line parts, for illustration, triangles, squares, and squares. Perimeter (peri around; meter measure) of a polygon is the distance or direct measure of these bounded line parts. In other words, it is the length of its boundaries. Its unit is centimetre (cm) or meter (m).
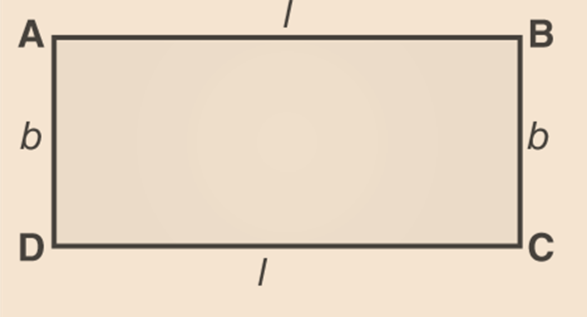
Perimeter of a rectangle,
Rectangle is a four- sided polygon having two range i.e. length and breadth.
Perimeter of a cube = sum of four sides
= AB + BC+ CD+ AD
= length + breadth +length+ breadth = 2 length +2 breadth
Perimeter of a rectangle = 2 × (length+ breadth)
Perimeter of a square
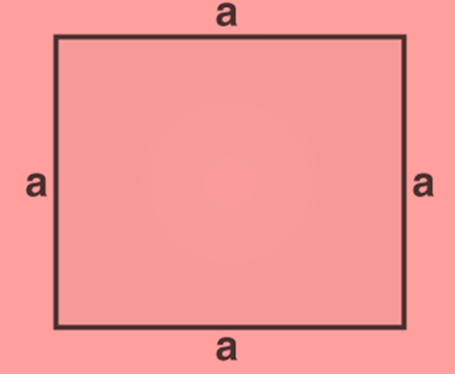
Square is also a polygon where all its sides are the same.
The perimeter of a square = sum of all four sides
= a + a + a+ a
= 4a
The perimeter of a square = 4 × side
The sum of the lengths of the sides is the perimeter of any polygon. In the case of a triangle,
Perimeter = Sum of the three sides
Always include units in the final answer. If the sides of the triangle are measured in centimetres, then the final answer should also be in centimetres.
Perimeter of a triangle
The formula for the perimeter of a closed shape figure is usually equal to the length of the outer line of the figure. Therefore, in the case of a triangle, the perimeter will be the sum of all the three sides. If a triangle has three sides a, b and c, then,
Perimeter, P = a + b +c
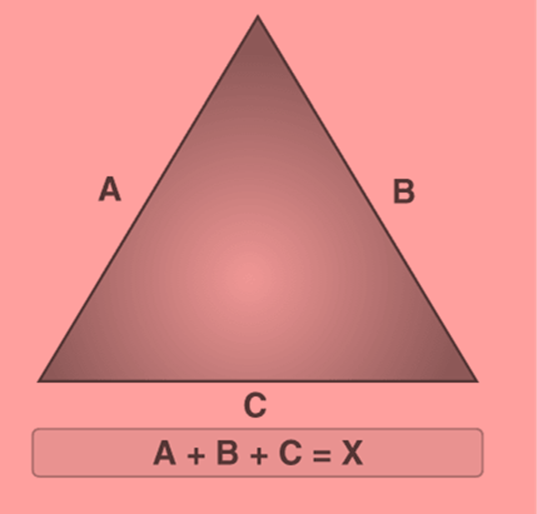
Perimeter of an Isosceles, Equilateral and Scalene Triangle
Below table helps us to understand how to find the perimeter of different triangles- Equilateral triangle, Isosceles triangle and Scalene triangle.
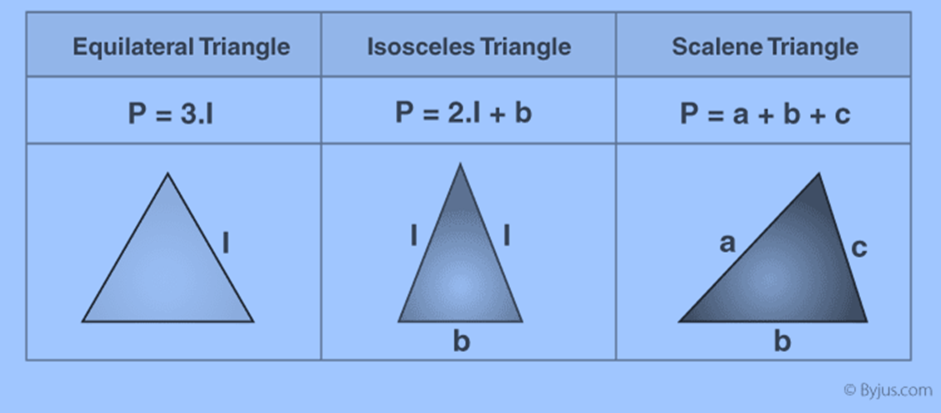
Perimeter of regular shapes
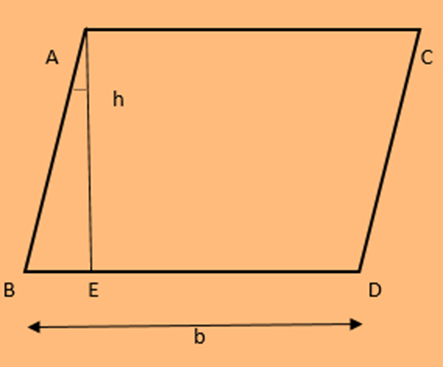
Perimeter of a parallelogram with Base, Height and an Angle
The perimeter of the parallelogram with base and height is given using the property of the parallelogram. If “b” is the base of the parallelogram and “h” is the height of the parallelogram, then the formula is given as follows:
According to the property of the parallelogram, the opposite sides are parallel to each other, and the parallelogram perimeter is defined as two times of the base and height.
Thus, the formula for the perimeter of a parallelogram is
P = 2 (b +h/cos θ)
where θ is the angle BAE, formed between the height and side of the parallelogram, i.e. AE and AB

 Carrier Point
Carrier Point
 ReginaTagebücher
ReginaTagebücher
