Area

Area
 

The amount of surface of the plane covered by a closed figure is called its area. For every closed figure, there are two regions.    

The term 'area' refers to the measure of the total interior region.
Closed figures given below. They are occuping  some region it is difficult to tell which figure occupies more region. It is difficult to make out unless we measure the area.

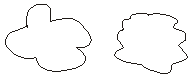
In order to calculate which closed figure having larger area we place them on a squared paper or graph paper where every square measures 1 cm × 1 cm. Make an outline of the figure.
Look at the square enclosed by the figure. Some of them are completely enclosed  some half, some less than half and some more than half.
The area is the number of centimeter squares that are needed to cover it.
But there is a small problem that the square do not always fit exactly into the area we measure. We get over this difficulty by adopting a convention.

• The area of one full square is taken as 1 sq unit. If it is a centimetre square sheet , then area of one full area will be 1 sq. cm.
• Ignore portions of the area that are less than half a square.
• If more than half of a square is in a region, just count it as one square.
• If exactly half the square is counted , take its area as sq unit.

Such a convention gives a fair estimate of the desired area.

Ex.1     Find the area of the shape shown in the figure.

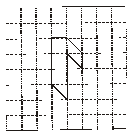
Sol. This figure is made up of line segments moreover, it is covered by full squares and half squares only. This makes our job simple.

        (i)     fully filled squares = 3
        (ii)     half filled squares = 3

Area covered by full squares = 3 × 1 sq units = 3 sq units 

 

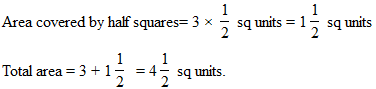
1.    Area of rectangle: For rectangle having length l unit and breadth b units. 

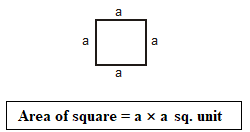
2.    Area of square: For square having side a unit. 

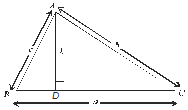
3.    Area of a triangle :

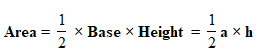
Ex.2    Find the side of a square whose area is 25 sq. m.
    Sol.     Now we find the number which when multiplied by itself gives us 25.
        clearly, this number is 5.
     ∴    Side of the square = 5m.

Ex.3     In given figure, find the area of the shaded portion when all dimensions are given in centimeters.

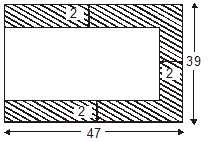
Sol.       Length of the bigger rectangle     = 47 cm
             Breadth of the bigger rectangle    = 39 cm
             Area of the bigger rectangle    = length × breadth
                        = (47 × 39) sq cm = 1833 sq cm
             Length of the smaller rectangle     = (47 –2) cm = 45 cm
             Breadth of the smaller rectangle     = (39 – 2– 2) cm = 35 cm
             Area of the smaller rectangle     = (45 × 35) sq cm 
                        = 1575 sq cm
                          Area of shaded portion     = (1833 – 1575) sq cm 
                        = 258 sq cm

Ex.4     In given figure, if the area of the triangle ABC is 36cm2 and the height AD is 3 cm then the base would be  

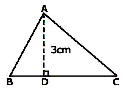
Sol.     Given area = 36 sq cm  and  height = 3 cm  base = ?
            Area of the triangle     = (base x height) ¸ 2
                36     = (base × 3) ¸ 2
                   Base     = (36 × 2) ¸ 3 = 24 cm

Ex.5     Bob wants to cover the floor of a room 3 m wide and 4 m long by squared tiles. If  each square tile is of side 0.5 m, then find the number of tiles required to cover the floor of the room.
Sol.:     Total area of tiles must be equal to the area of the floor of the room. 
            Length of the room     = 4 m
            Breadth of the room     = 3 m
            Area of the floor     = length × breadth 
                      = 4 m × 3 m = 12 sq m
            Area of one square tile     = side × side
                    = 0.5 m × 0.5 m
                    = 0.25 sq m

Ex.6    Find the area in square metre of a piece of cloth 1m 25 cm wide and 2 m long.
Sol.     Length of the cloth = 2 m
           Breadth of the cloth= 1 m 25 cm = 1 m + 0. 25 m = 1.25 m    (since 25 cm = 0.25m)
           Area of the cloth = length of the cloth × breadth of the cloth = 2 m × 1.25 m = 2.50 sq m