- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Algebric Equation
An equation is a mathematical statement equating two quantities. An equation has an equal sign (=) between its two sides. The equation says that the value of the left hand side (LHS) is equal to the value of the right hand side (RHS). If the LHS is not equal to the RHS, we do not get an equation.
Equation is satisfied only for a definite value of the variable.
There is an equal sign between the LHS and RHS. Neither of the two sides contain a variable. Both contain numbers. We may call this a numerical equation. Usually, the word equation is used only for equations with one or more variables.
Here are some examples of equations : 2x– 5 = 7, –3x + 2 = 5, y + 3 = 0
Solution of an equation
The value of the variable (unknown) in an equation which satisfies the equation is called a solution to the equation.
The values is called the root(s) of the equation or solution of the equation.
Let us take an example of an equation x + 3 = 10.
We have to find the value of x which will satisfy the above equation. And we observe that if we put
x = 7 in this equation it will satisfy the equation. So x = 7 is the solution or root of this equation.
Solution of an equation by trial an error
One of the simplest ways of solving an equation is by the trial-and-error method. In this, a guess is made about the value of x, and this value is then substituted in the equation to check if it is the root of the equation. Consider the following example : 4x + 3 = 23
Our equation is 4x + 3 = 23. So we substitute different values for x and try to find out which value of x will satisfy the equation. Make a chart as follow.
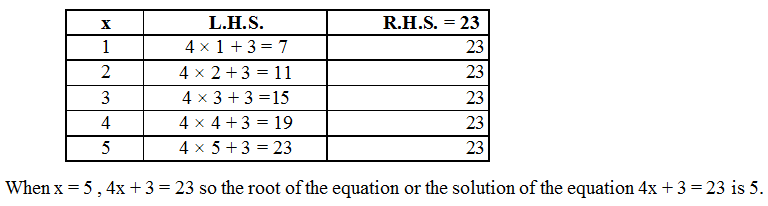
Ex.1 Determine if 3 is the root of the equation 5x – 10 = 5.
Sol. If we put x = 3, then L.H.S. = 5x – 10 = 5 × 3 – 10 = 15 – 10 = 5
R.H.S. = 5
∴ L.H.S. = R.H.S
Thus, 3 is a root of the given equation.
Ex.2 If 20 is subtracted from a number, the result is 45. Convert this statement into an algebraic equation.
Sol. Let us suppose that x is the unknown number.
Then x – 20 stands for 20 subtracted from the number x. This is equal to 45.
Hence, x – 20 = 45
Once you convert a statement into an algebraic equation, it is easier to solve and find the root.
Ex.3 Solve the equation x – 7 = – 2 and check the result.
Sol. We have, x – 7 = – 2.
In order to solve this equation, we have to get x by itself on the L.H.S., We need to shift – 7. This can be done by adding 7 to both sides of the given equation. Thus,
x – 7 = – 2
⇒ x – 7 + 7 = – 2 + 7 [Adding 7 to both sides]
⇒ x + 0 = 5 [∵ – 7 + 7 = 0 and – 2 + 7 = 5]
⇒ x = 5
Thus, x = 5 is the solution of the given equation.
L.H.S. = 5 – 7 = – 2 and R.H.S. = – 2
Thus, when x = 5, we have L.H.S. = R.H.S.
Ex.4 Solve : 3(x + 3) – 2 (x – 1) = 5 (x – 5).
Sol. We have,
3(x + 3) – 2(x – 1) = 5(x – 5)
⇒ 3x + 9 – 2x + 2 = 5x – 25 [Expanding brackets on both side]
⇒ 3x – 2x + 9 + 2 = 5x – 25
⇒ x + 11 = 5x – 25 [Taking 5x to the L.H.S. and 11 to the R.H.S.]
⇒ – 4x = – 36
∴ x = 9

 Param Publication
Param Publication
