1. Introduction to The Whole Numbers
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Introduction
As we know, we use 1, 2, 3, 4,... when we begin to count. They come naturally when we start counting. Hence, mathematicians call the counting numbers as Natural numbers.
Predecessor and successor
Given any natural number, you can add 1 to that number and get the next number i.e. you get its successor. The successor of 16 is 16 + 1 = 17.
Similarly, if we substract 1 from that number we get predecessor of that number, the predecessor of 20 is 20 – 1 = 19.
Whole Numbers
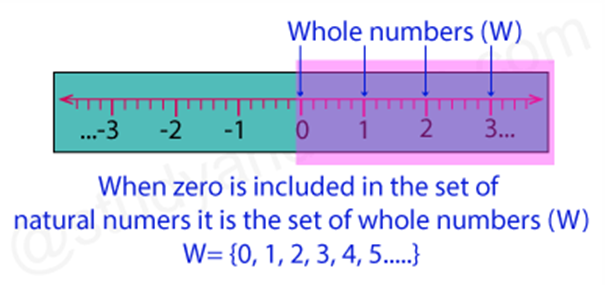
The numbers 1, 2, 3, ...., are called natural numbers or counting numbers. Let us add one more number, i.e., zero (0), to the collection of natural numbers. Now the numbers are 0, 1, 2, 3, ..... These numbers are called whole numbers.
1. Introduction to The Whole Numbers
- Books Name
- Mayank classes Mathematics Book
- Publication
- Mayank classes
- Course
- CBSE Class 6
- Subject
- Mathmatics
Microorganisms
What are Microbes?
Microbes or microorganisms are tiny organisms which are so small that we cannot see them with an unaided eye. Some microorganisms can be seen with the help of a magnifying glass (such as fungus that grows on bread) while some can only be seen when you use a microscope (such as bacteria and protozoa). Microorganism were first observed by Anton Van Leeuwenhoek.Viral, Bacterial, and Protozoan Diseases
A microorganism or microbe is a microscopic organism that may exist in its single-celled or colony of cells.
Nature and occurrence: -
▪ Life on earth depends on microorganisms. They play a very critical role in the ecosystem of our planet. Microbes perform the important role of breaking down dead organisms into the basic nutrients that are essential for life on our planet.
▪ Bacteria, fungi, algae, and protozoa are the 4 major groups of microbes.
▪ Viruses are another class of microbes which totally depend on the host for food, growth and reproduction. They are incapable of independent existence.
▪ Nature: Microbes may be unicellular e.g. bacteria, protozoa, or multicellular (2 or more cells) e.g. some Algae and Fungi.
Features of Micro-organisms
- Microorganisms are too small and are not visible with the naked eye.
- They can live in all kinds of environment, ranging from ice cold climate to hot springs, deserts and marshy lands.
- Microorganisms are found in air, water and in the bodies of plants and animals.
- They may be unicellular or multicellular.
- Microorganisms include bacteria, fungi, protozoa and some algae. Viruses though different from the above-mentioned living organisms are referred to as microbes.
- Viruses are quite different from other microorganisms. They reproduce only inside the cells of the host organism: bacterium, plant or animal.
Microorganisms
There are four major types of microorganisms:
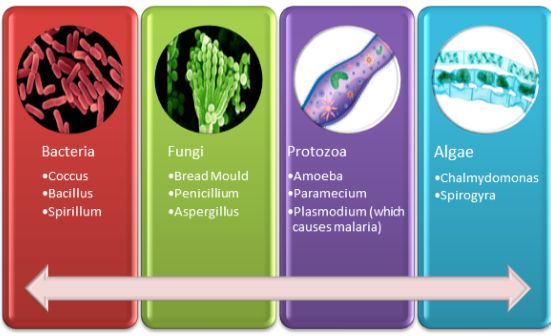
Fig 1: Types of Microorganisms
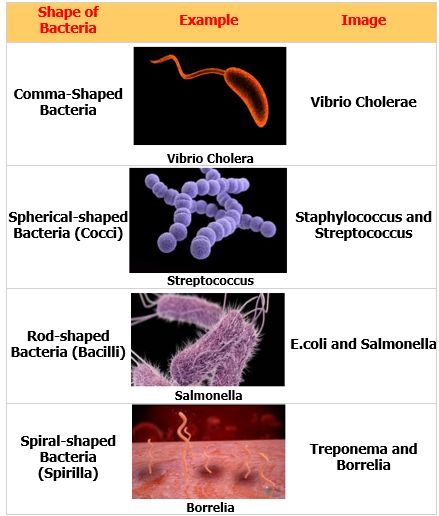
Bacteria: These are single-celled organisms with a rigid cell wall. They can only be seen under a microscope which enlarges images from 100 to 1000 times.
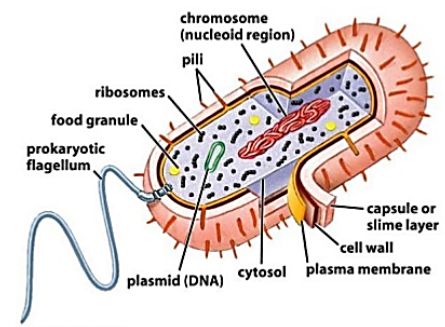
Ultrastructure of a Bacterial Cell
Types of Bacteria (based on their Shapes) and their Examples
- Fungi: These are non-green plants and hence, cannot make their own food. They either live as parasites (deriving nutrition from host organisms, for example, Puccinia which causes wheat leaf rust) or grow on the organic matter (such as bread mould).

Puccinia triticina
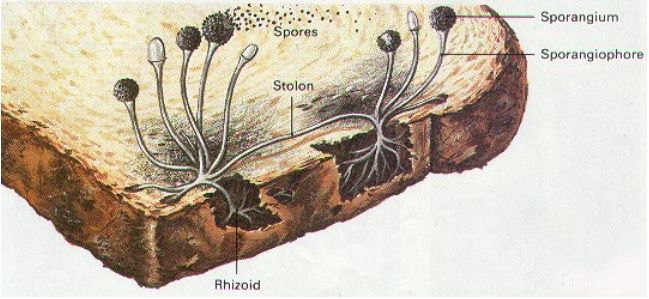
Fig 8: Bread Mould
- Fungi, like mushrooms, moulds, mildews, and years, are eukaryotic. It means that they have a true nucleus.
- The main components of fungi are:
- i. Hyphae: They are thread-like filaments which penetrate into substrates, secrete enzymes to break down nutrients into smaller molecules, and absorb them.
- ii. Spores are a unit of sexual or asexual reproduction. They can adapt for dispersal and survival for extended periods of time in unfavourable conditions.
- Algae: These are simple plant- like organisms which are usually aquatic in nature. They contain a cell wall and chlorophyll and can make their own food by photosynthesis. Algae can be unicellular or multicellular. Some of the common examples are diatoms, Chlamydomonas, and seaweed.
- Protozoa: Protozoa are unicellular organisms. Some of them live independently while others live as parasites. Many of the parasitic protozoans cause diseases in plants, domestic animals, and human beings. Example of some protozoans are Amoeba, Plasmodium and Paramecium
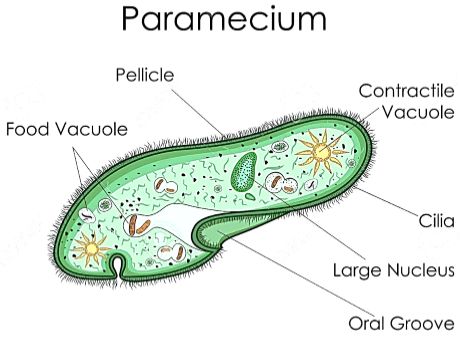
Fig 9: Paramecium
How are Viruses different from other microbes?
- Viruses are microscopic organisms but they are different from other microbes because they reproduce only inside the cells of the host organism (which can be a plant, animal, or a bacterium).
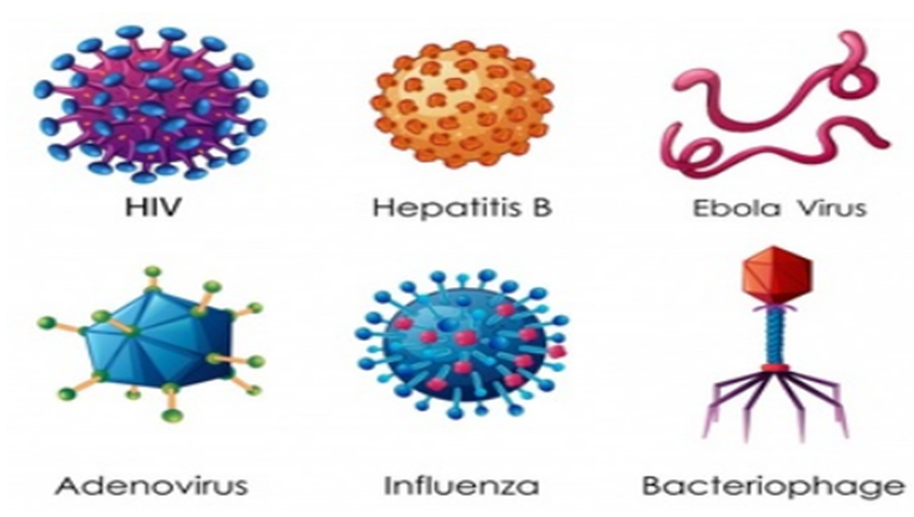
Types of Viruses
- Viruses are much smaller than bacteria and come in a wide variety of shapes and sizes. A complete virus particle is known as Virion.
Virion consists of a nucleic acid surrounded by 'capsid'. Capsid is a protective coat made of protein. The subunits of this protein called 'Capsomeres'. Viruses can be seen only by an electron microscope as they are ultramicroscopic in size. - Outside the body of a living organism, they do not show any reaction and hence, can be crystallized and stored like non-living things.
1. Introduction to The Whole Numbers
- Books Name
- Class 6 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 6
- Subject
- Mathmatics
Chapter 2
Whole Numbers
What are whole Numbers?
Let’s begin with natural Numbers.

When we begin to count we naturally use counting Numbers {1, 2, 3, 4.}. Hence, Natural Numbers are the numbers starting from number 1 to infinity
We represent natural Numbers by ‘N’.
Or we can say N = {1, 2, 3, 4.} (i.e. 1 to infinity)
For Every natural number, there is a predecessor and a successor.
For Example: Predecessor of 2 is 1 and
Successor of 2 is 3.
The set of natural Numbers along with zero are called whole Numbers. The set of Whole Numbers without decimal or fractional Numbers.
We represent whole Numbers by ‘W’.
Or we can say W = {0, 1, 2, 3, 4.} (i.e. 0 to Infinity)
Important Note
1. We can get successor of a whole number by adding 1 to the given whole number.
E.g. 9
Then, number is 9.
Successor = 9+ 1 = 10
every whole number has its successor.
2. We can get predecessor of whole number by subtract 1 from given whole number.
Illustration 23
Then, number is 23
Precursor = 23-1 = 22
3. Zero has no predecessor.
4. The lowest whole number is‘0’.
5. There's no largest number in set of whole Numbers.
6. Every whole number without ‘zero’ is a natural number
2. Properties and Patterns of Whole Numbers
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Properties of multiplication
(i) Closure Property : If a and b are whole numbers, then their product a x b = c will always be a whole number. That is whole numbers are closed under multiplication.
For ex. 7 x 3 = 21x 6 x 8 = 48 x 3 x 0 = 0
(ii) Commutative Property : In general a x b = b x a for all whole numbers a and b.
Consider the following example
2 x 3 = 3 x 2 = 6
8 x 9 = 9 x 8 = 72
(iii) Associative Property : If a,b and c are whole numbers, then (a x b) x c = a x (b x c)
That is, whole numbers have the associative property of multiplication.
For ex. (3 x 4) x 2 = 3 x (4 x 2)
12 x 2 = 3 x 8
24 = 24
(iv) Multiplicative Identity : 1 x a = a x 1 = a. Hence, 1 is called the multiplicative identity for whole numbers.
For ex. 10 x 1 = 1 x 10 = 10
3 x 1 = 1 x 3 = 3
672 x 1 = 1 x 672 = 672
0 x 1 = 1 x 0 = 0
Properties of division
(i) Closure Property : If a and b are whole number , then the quotient a ÷ b need not always be a whole number. So, division in whole numbers is not closed.
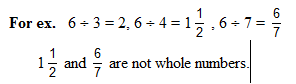
Commutative Property : If a and b are whole numbers, then a ÷ b is not equal to b ÷ a. So, the commutative property does not hold true for whole numbers.
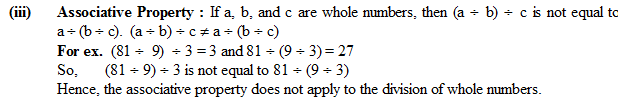
2. Properties and Patterns of Whole Numbers
- Books Name
- Class 6 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 6
- Subject
- Mathmatics
Properties and patterns of whole Numbers
Properties of Whole Numbers

1. Closure Property
2. Associative Property
3 Commutative Property
4. Distributive Property
1.Closure Property of Whole Numbers
This property tells us that when whole number is operated on "Addition and multiplication” their answer is always in Whole Number.
This property does not be same as on whole numbers in the while doing division and subtraction.
For example: Two whole numbers subtracted then answer will not be whole number, 2 and 4 are whole numbers, but 2 - 4 = -2, is not a whole number. Same in the case of division, 2/4 is not defined
Associative Property of Whole Numbers
This property tells us that "The answer of the sum and the product of whole numbers remain the same, if the numbers are three whole numbers
Example 1: (1+2)+3 = 1+(2+3) because,
(1+2)+3 = 3+3 = 6
1+(2+3) = 1+5 = 6
Example 2: (1×2) × 3 = 1 × (2×3) because,
(1×2) × 3 = 2 × 3 = 6
1 × (2×3) = 1 × 6 = 6
This property of whole numbers does not same for division and subtraction operations.
For example, 4, 5, and 6 are whole numbers, but 4 - (5 - 6) = 4 - (-1) = 5 and (4 - 5) - 6 = - 1 - 6 = -7. So, 5 ≠ 7.
The same is with the division where 9 ÷ (6 ÷ 3) ≠ (6 ÷ 3) ÷ 9.
Commutative Property of Whole Numbers
“After interchanging the order of the numbers, the sum and the product of two whole numbers always are the same number”.
Example 1: 4+5 = 5+4 because,
4+5 = 9
5+4 = 9
Example 2: 4×2 = 2×4 because,
4×2 = 8
2×4 = 8
the commutative property of whole numbers does not always be the same for on division and subtraction.
Distributive Property of Whole Numbers
The distributive property of multiply and sum is
A× (b+c) = a×b+a×c.
Example 1: 3× (2+5) = 3×2+3×5 because,
3× (2+5) = 3×7 = 21
3×2+3×5 = 6+15 = 21
the distributive property of multiply and subtract is a× (b−c) =a×b−a×c.
Example 2: 3× (5−2) = 3×5−3×2 as,
3× (5−2) = 3×3 = 9
3×5-3×2 = 15-6 = 9
Patterns in whole numbers
Patterns are defined as the sequence that follows a defined sequence or patterns
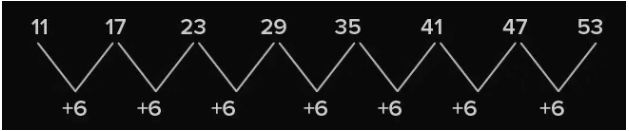
Here the numbers are 11, 17, 23, 29, 35, 41, 47, and 53. The
The numbers are increasing by count of 6 every time.
Using Dots Number Patterns
Every whole number is defined in the form of dots and to find the pattern numbers are arranged in the dots representation. These representations are A rectangle, A square, A triangle
Properties Of Addition & Substraction
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Properties Of Addition & Substraction
Properties of Addition
(i) Closure Property : If ‘a’ and ‘b’ are two whole numbers and their sum is c, i.e., a + b = c,
then c will always be a whole number. This property of a addition is called the closure property of addition.
For ex. : 2 + 8 = 10 i.e., whole number + whole number = whole number
(ii) Commutative Property : If a and b are two whole numbers a + b = b + a. This property of addition, where the order of addition does not alter the sum, is called the commutative property of addition
For ex. 3 + 4 = 7
Also, 4 + 3 = 7
i.e., 3 + 4 = 4 + 3
(iii) Associative Property : If a, b and c are three whole numbers, then a + (b + c) = (a + b) + c. In other words, in the addition of whole numbers, the sum does not change even if the grouping is changed. This property is called the associative property of addition.
For ex. 2 + (3 + 4) = (2 + 3) + 4
2 + 7 = 5 + 4
9 = 9
(iv) Additive Identity : If a is a whole number ,then a + 0 = 0 + a = a.
Hence, zero is called the additive identity of the whole numbers because it maintains (or does not change) the identity (value) of the numbers during the operation of addition.
For ex. 7 + 0 = 7 = 0 + 7
Properties of subtraction
(i) Closure Property : If a and b are two whole numbers, then a – b will be a whole number only if a is greater than b or a is equal to b. If a is smaller than b, then the answer will not be a whole number. Hence, subtraction is not closed under whole numbers.
For ex. 7 – 2 = 5 is whole number
but 3 – 8 is not a whole number
(ii) Commutative Property : If a and b are two distinct whole numbers, then a – b is not equal to b – a. Hence, the commutative property is not true for subtraction of whole numbers.
For ex. a – b ≠ b – a
7 – 2 ≠ 2 – 7
(iii) Associative Property : If a, b and c are whole numbers, then (a – b) – c is not equal to a – (b – c). So, the associative property also does not hold true for subtraction of whole numbers
For ex. (12 – 4) – 3 = 8 – 3 = 5
12 – (4 – 3) = 12 –1 = 11
Therefore (12 – 4) – 3 ¹12 – (4 – 3)
The Number Line
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
The Number Line
We draw a line. Mark a point on it. Label it 0. Mark a second point to the right of 0. Label it 1.
The distance between these points labelled as 0 and 1 is called unit distance.
On this line, mark a point to the right of 1 and at unit distance from 1 and label it 2. In this way labelling points at unit distances as 3, 4, 5,... on the line. We can go to any whole number on the right in this manner. This is a number line for the whole numbers.
![]()
Addition on the number line
Addition of whole numbers can be shown on the number line. Let us see the addition of 3 and 4.
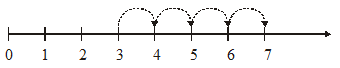
Start from 3. Since we add 4 to this number so we make 4 jumps to the right; from 3 to 4, 4 to 5, 5 to 6 and 6 to 7 as shown above. The tip of the last arrow in the fourth jump is at 7.
The sum of 3 and 4 is 7, i.e. 3 + 4 = 7.
Subtraction on the number line
The subtraction of two whole numbers can also be shown on the number line. Let us find 7 – 5.

Start from 7. Since 5 is being subtracted, so move towards left with 1 jump of 1 unit. Make 5 such jumps. We reach the point 2. We get 7 – 5 = 2.
Multiplication on the number line
We now see the multiplication of whole numbers on the number line. Let us find 4 × 3.

Distributed Property
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics


 Param Publication
Param Publication
 ReginaTagebücher
ReginaTagebücher
