1. Introduction to The Fractions
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Fractions
A fraction is a number representing a part of a whole. It is written as ![]() where a is the numerator and b is the denominator.
where a is the numerator and b is the denominator.
![]()

Fraction as a Part of a Whole :
If a birthday cake is divided into four equal parts, each part is represented as 1 part out of 4 equal parts and is written as ![]()
The part that is considered (in this case, 1) is called the numerator. The number of parts into which the whole is divided (in this case, 4) is called the denominator.
![]() is a fraction. We read it as “five-twelfths”. Here 12 stands for the number of equal parts into which the whole has been divided and 5 stands for the number of equal parts which have been taken out.
is a fraction. We read it as “five-twelfths”. Here 12 stands for the number of equal parts into which the whole has been divided and 5 stands for the number of equal parts which have been taken out.
Here 5 is called the numerator and 12 is called the denominator.
Ex. What fraction of a day is 9 hours?
Sol. One day = 24 hours
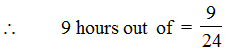
i.e., 9 hours out of 24 hours.
![]()
Fraction on the Number Line
In previous chapters we learnt to show whole numbers like 0,1,2... on a number line. We can also show fractions on a number line. Let us draw a number line and we try to mark ![]()
is greater than 0 and less than 1, so it should lie between 0 and 1.
Since we have to show ![]() we divide the gap between 0 and 1 into two equal parts and show 1 part as
we divide the gap between 0 and 1 into two equal parts and show 1 part as ![]() (As shown in figure)
(As shown in figure)
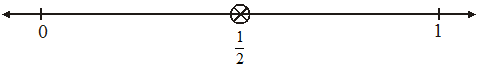
Suppose we want to show ![]() on a number line. We divide the length between 0 and 1 into 3 equal partsand show one part as
on a number line. We divide the length between 0 and 1 into 3 equal partsand show one part as ![]() (as shown in the Figure)
(as shown in the Figure)

1. Introduction to The Fractions
- Books Name
- Class 6 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 6
- Subject
- Mathmatics
Chapter 7
Fractions
Introduction to The Fractions
A fraction is a number representing a part of a whole. The total may be a single object or a group of objects. The other way round, we can say that a fraction is an operation on a number.
A Fraction
A fraction means a part of a group or of a region. 34 is a fraction. We read it as “ Three- fourths ”.
The first one is the whole i.e. a complete circle.
In the alternate circle, if we divide the circle into two equal corridor then the shadowed portion is the half i.e. ½ of the circle.
In the third circle, if we divide the circle into four equal corridor and shade only one part then the shadowed part is the one fourth i.e. ¼ of the whole circle.
In the fourth circle, if we divide the circle into four equal corridor and shade three corridor then the shadowed part is the three fourth i.e. ¾ of the whole circle.
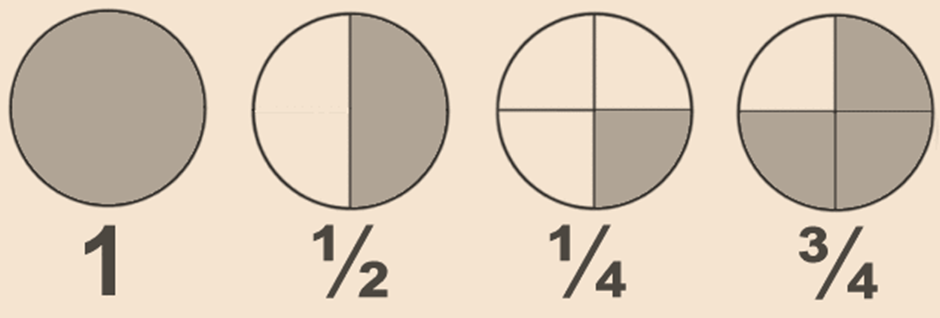
Then, four stages for the number of equal region into which the total has been divided and three stages for the number of equal region, which have been taken out.
2. Fraction and its Classification
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Types of Fractions
(i) Proper Fractions : A proper fraction is a fraction in which the numerator is smaller than the denominator.

(ii) Improper Fractions : An improper fraction is a fraction in which the numerator is greater than the denominator.
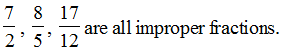
(iii) Mixed fraction : Fractions such as ![]() are called Mixed Fractions. A mixed fraction has a combination of a whole and a part.
are called Mixed Fractions. A mixed fraction has a combination of a whole and a part.
Ex. Express the following as mixed fraction :
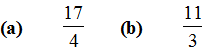
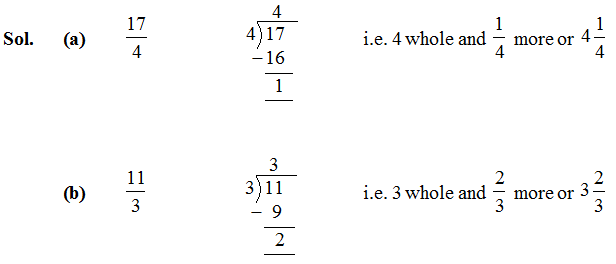
Conversion of Mixed Fractions into Improper Fractions

2. Fraction and its Classification
- Books Name
- Class 6 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 6
- Subject
- Mathmatics
Fraction and its Classification
Fraction and its types,
It has to be noted that while expressing a situation of counting region to write a fraction, all region must be equal.

Then, three is called the numerator and 4 are called the denominator.
Numerator and denominator can be linked for any fraction.
The upper part of the fraction is called Numerator.
It tells the number of region we have.
The lower part of the fraction is called Denominator.
It tells the total region in a whole.
It reads as" three- fifths"
Proper and Improper fraction,
Proper Fractions
If the numerator is bigger than the denominator then it's called proper bit. If we represent a proper bit on the number line than it'll always lie between 0 and 1.
Example:
Improper fractions and mixed fractions
When the numerator is bigger than the denominator then it's called Improper bit.
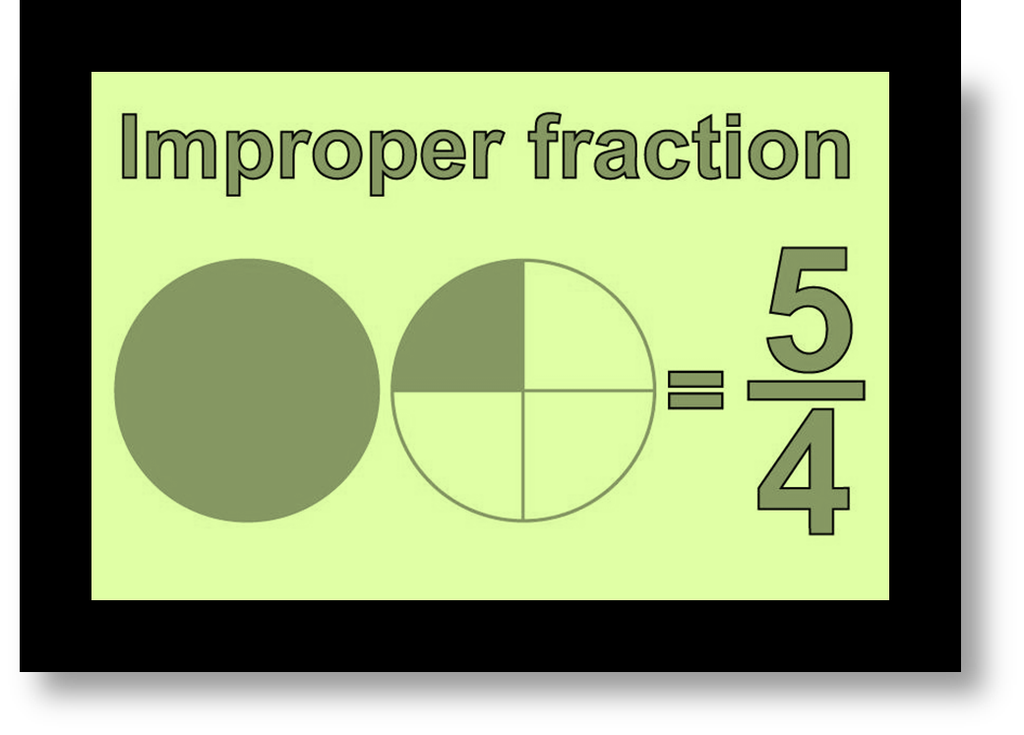
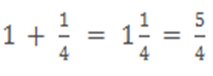
The above fraction is made by adding one whole part and one- fourth part.
Mixed Fraction
The bit made by the combination of whole and a part is called mixed bit.
Convert mixed bit into improper bit
A mixed bit is in the form of
Fractions

We can convert it in the form of an improper fraction by
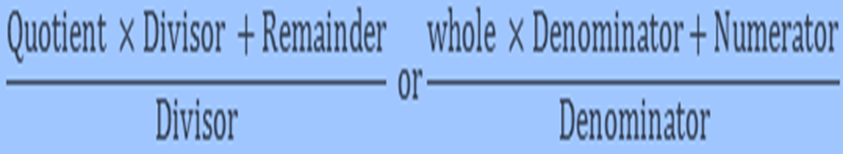
Example

Answer
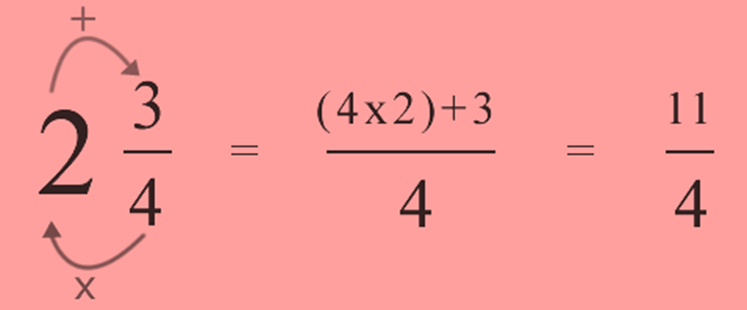
Like fractions and unlike fractions
Fractions that have same denominators are known as Like fractions.
Equivalent fraction
Equivalent fractions
Equivalent fractions are those fractions which represent the same part of a whole.
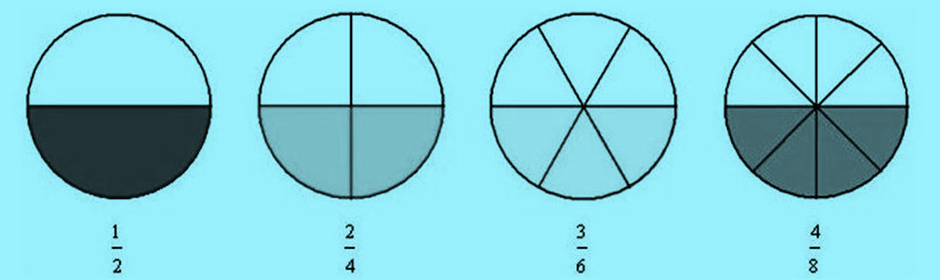
All the above images are different but Equivalent fractions as they represent the same i.e. half part of a whole circle.
Finding Equivalent fractions:
Multiplying the same number
If we multiply the numerator and denominator of any bit with the same number then we will get the Equivalent bit. There could be other than one Equivalent fractions of one bit.
Example
Find three Equivalent fractions of ½.
Answer:
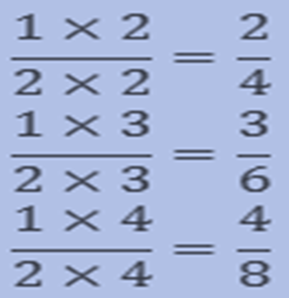
Dividing the same number
If we divide the numerator and denominator of any bit with the same number then we will get the Equivalent fractions.
Example
Find the Equivalent fraction of 18/27 with denominator 9.
Answer
To get the denominator 9 we need to divide it by 3.
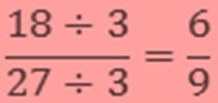
Therefore, to find the Equivalent fraction we need to divide the bit by 3.
Hence, the Equivalent fraction with denominator 9 is 6/9.
The simplest form of a fraction
If the numerator and denominator don't have any other common factor than 1 then it's said to be the simplest or smallest form of that bit.
Example-
To find the Equivalent fraction which is the simplest form we've to find the HCF of numerator and denominator and then divide them both by that HCF.
Example
Reduce the fraction18/27 in the simplest form.
Answer
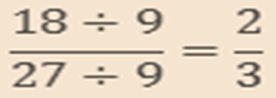
HCF of 18 and 27 is 9.
Hence, 2/3 is the smallest form of18/27.
Simplest form of fraction
Fractions that have different denominators are known as unlike fractions.
Example

Comparing fractions
If we've to compare the above two fractions then it's easy as the first one is lower than 3 and the alternate bone
is bigger than 3. So we can easily say that
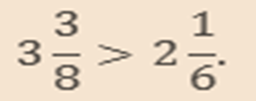
But occasionally it isn't easy to compare it so fluently. So we need some accurate procedure.
Comparing like fractions
Like fractions are the fractions with the same denominator so we've to compare them with the numerator only. The fraction with bigger numerator is bigger.
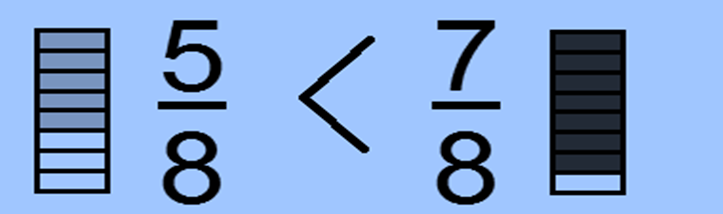
In the above example, both are divided into 8 equal corridors, so the bit with seven-shadowed part is bigger than the 5-shadowed corridor.
Comparing unlike fractions
The fractions with different denominators are unlike fractions.
Unlike fraction with the same numerator
Still, we have to compare with the denominator only, if we have to compare the fractions with different denominator but same numerator.
In that case, the bit with the small denominator is bigger than the other.
Example
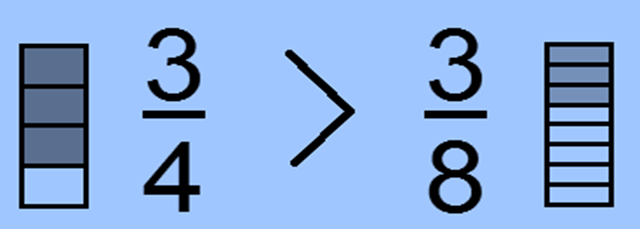
Then the numerator is same i.e. 3 so we will compare with the denominator.
The bit with small denominator i.e. ¾ is bigger than the bit with the large denominator i.e.3/8.
Unlike fraction with different numerators
If the numerator and denominator both are different then we have to make the denominator same by finding the Equivalent fraction of both the fractions then compare the fractions as like fractions.
To find the Equivalent fraction of both the fractions with the same denominator, we've to take the LCM of the denominator.
Example
Compare 6/7 and3/5.
Answer
The product of 7 and 5 is 35.
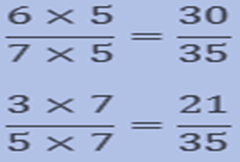
Therefore, we will find the Equivalent fraction of both the fractions with the denominator 35.

Now we can compare them as like fractions.
3. Addition and Subtraction of Fractions
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Equivalent Fractions
Let us take some pictorial representation of fraction.
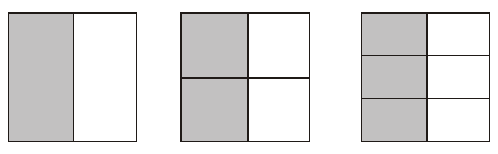
These fractions are 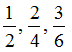 representing the parts taken from the total number of parts. If we place the pictorial representation of one over the other they are found to be equal.
representing the parts taken from the total number of parts. If we place the pictorial representation of one over the other they are found to be equal.
These fractions are called equivalent fractions.
Understanding equivalent fractions
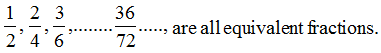
They represent the same part of a whole.
There are two ways of obtaining equivalent fractions.
(a) By multiplying its numerator and denominator by the same number.
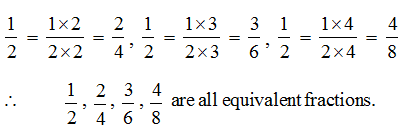
(b) By dividing its numerator and denominator by the same number.
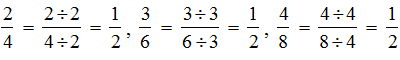
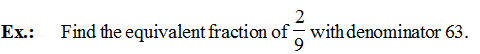
Sol.: We know 2 × 3 = 6. This means we need to multiply both the numerator and the denominator by 3 to get the equivalent fraction.

Simplest Form of a Fraction
A fraction is said to be in the simplest (or lowest) form if its numerator and denominator have no common factor except 1.
The shortest way
The shortest way to find the equivalent fraction in the simplest form is to find the HCF of the numerator and denominator, and then divide both of them by the HCF.
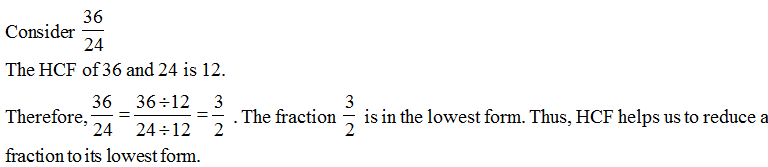
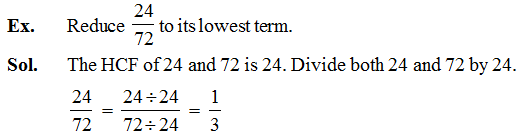
3. Addition and Subtraction of Fractions
- Books Name
- Class 6 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 6
- Subject
- Mathmatics
Addition and Subtraction of fractions
Adding like fractions
In case of like fractions, the denominator is same so we can add them fluently.
Steps to add like fractions-
Add the numerators.
Leave the common denominator same. (Do not add the denominator).
Write the answer as

Example
![]()
Answer
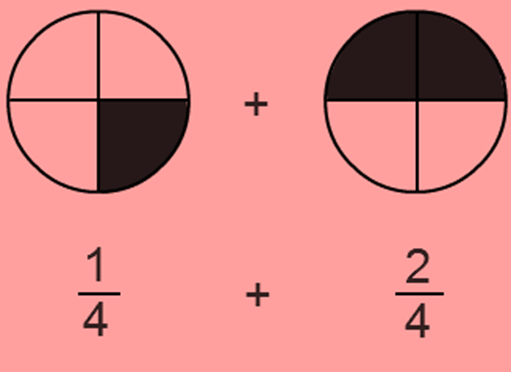
Solutions:

Subtracting like fractions
Steps to subtract the like fractions-
Subtract the small numerator from the bigger one.
Leave the common denominator same.
Write the answer as

Example:
![]()
Solution:
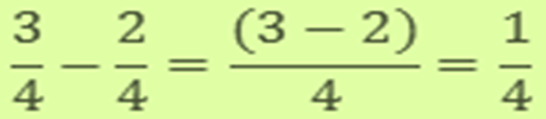

Adding unlike Fraction
Still, first we have to find the Equivalent bit of the given fractions with the same denominator then add them, if we have to add the unalike fractions.
Steps to add unlike fractions-
Take the LCM of the denominator of the given fractions.
Find the Equivalent fractions of both fractions with LCM as the denominator.
Add them as such like fractions.
Example
![]()
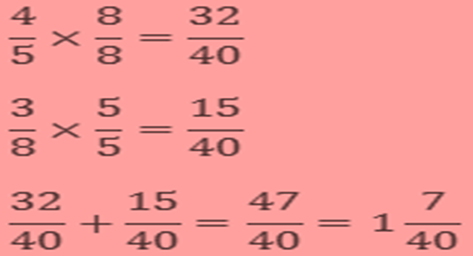
Take the LCM of 5 and 8, which are 40.
Subtracting unlike Fractions
Steps to subtract unlike fractions-
Take the LCM of the denominator of the given fractions.
Find the Equivalent fractions of both fractions with LCM as the denominator.
Subtract them as such like fractions.
Example
![]()
Answer
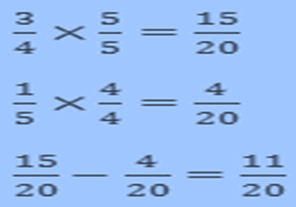
LCM of 4 and 5 is 20.
Comment: To add or abate the mixed fractions, simply convert them in the improper bit then add and abate them directly
Mixed fraction,
Like and Unlike Fractions
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Like and unlike Fractions
Fractions with same denominators are called like fractions.
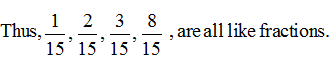
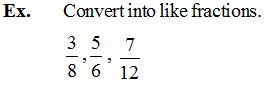

Comparing Fractions
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Comparing Fractions
For comparing two or more fractions, First we check their numerator and denominator with each other i.e. they are like or unlike.
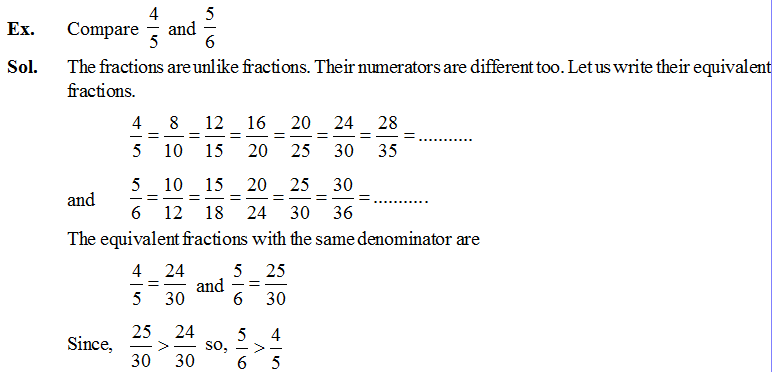
So, when we compare two unlike fractions, we first get their equivalent fractions with a denominator which is a common multiple of the denominators of both the fractions.
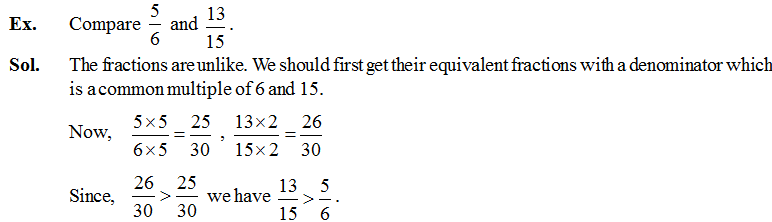
Adding and Subtracting Fractions
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Adding and subtracting fractions
Addition and subtraction is performed in like fractions. It is also not very difficult to add fractions that do not have the same denominator. When we have to add or subtract fractions we first find equivalent fractions with the same denominator and then proceed.


Adding and Subtracting with Mixed Fractions
- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Addition and subtraction with mixed fractions
Mixed fractions can be written either as a whole part plus a proper fraction or entirely as an improper fraction. One way to add (or subtract) mixed fractions is to do the operation seperately for the whole parts and the other way is to write the mixed fractions as improper fractions and then directly add (or subtract) them.

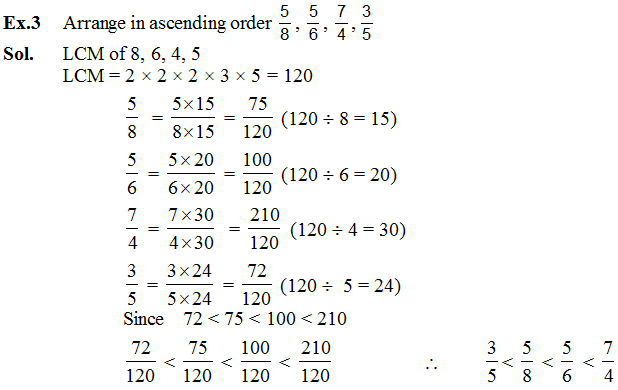

 Param Publication
Param Publication
 ReginaTagebücher
ReginaTagebücher
