- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Ratio
A ratio is a comparison of two numbers (quantities) by division. A ratio is usually denoted by the symbol (:). The ratio of a to b (b ≠ 0) is written as a : b or ![]()
In the ratio a : b, a and b are called terms of the ratio. 'a' is the antecedent and 'b' is the consequent.
A ratio is a number, so to find the ratio of two quantities they must be expressed in the same units.
Properties of Ratios
(a) In a ratio, two quantities are compared. So, the quantities must be of the same kind. i.e., they must be expressed in the same units.
(b) The value of a ratio remains unaltered if the given ratio is multiplied or divided by the same non-zero quantity.
(c) The order of the terms in a ratio a : b is very important. The ratio 3 : 2 is different from the ratio 2 : 3.
Ratio in the simplest or lowest form :
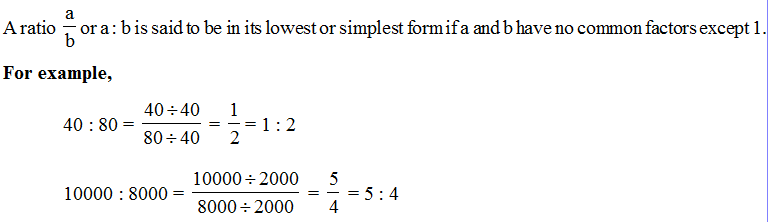
Ex.1 Find the ratio of the following :
(a) 36 minutes to 2 hours.
(b) 32 g to 1 kg
(c) 3 days to 1 years.
Sol. (a) Change both 36 minutes and 2 hours to the same unit.
Now, 36 minutes = 36 minutes
2 hours = 2 × 60 minutes = 120 minutes
∴ Ratio of 36 minutes to 2 hours
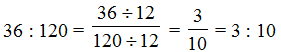
(b) First convert both into numbers with the same unit.
32 g = 32 g
3kg = 3000 g

(c) First , convert both into numbers with the same unit.
3 days = 3 days
1 year = 365 days
Ratio = 3 : 365
Ex.2 Find the (i) ratio of M20 to M80 (ii) ratio of 3 km to 600m
Sol. (i) 20 : 80 or 1 : 4
(ii) 3000m : 600m or 3000 : 600 or 5 : 1
Comparison of Ratios :
1. Write the given ratios as fractions in the simplest form.
2. Find the LCM of the denominators of the fractions.
3. Convert them into like fractions with same denominators .
4. Compare the numerators and arrange the fractions.
5. Then respective ratios are also in the same order.
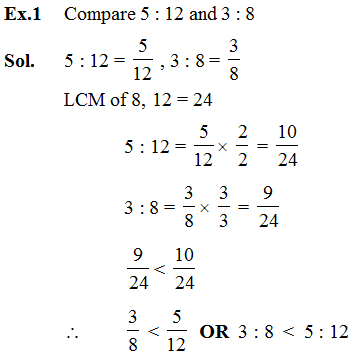
Ex.2 Two numbers are in the ratio 4 : 5. If the sum of the number is 63, then find the numbers.
Sol. Here 63 is to be divided in the ratio 4 : 5.
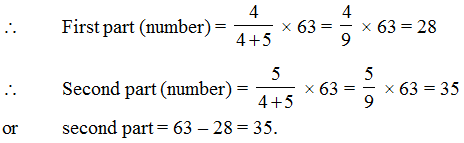
Ex.3 Mr. Harry divided Rs. 84,630 between Shinchan and Nimavari in the ratio 3 : 4. How much did each of them get ?
Sol. Ratio of money between Shinchan and Nimavari = 3 : 4
Sum of the terms of the ratio = 3 + 4 = 7

- Books Name
- Class 6 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 6
- Subject
- Mathmatics
Chapter 12
Ratio and Proportion
Ratio and its Comparison
Recalling about fractions
It is common to compare two amounts that are of same type. We compare prices of two belongings, height to of two people, size of different belongings, age of people etc.
For e.g. Let the price of a booklet is Rs. 10 and the price of a diary is Rs. 30.
Hence,
We get that the price of a diary is Rs. 20(Rs30 – Rs10) added than the price of a booklet. However, if we wish to compare the prices of these two belongings again taking the difference is not enough to express the comparison.
Therefore, we use ratio. In many situations, calculating the proportion is considered as an added meaningful way of comparing quantities. It is obtained by using division, i.e. by seeing how many times one quantity is to the other quantity. This method is known as comparison by ratio.
For example, the price of a booklet is Rs. 10 and price of a diary is Rs. 30.
We say that price of a diary and price of a booklet are in the rate 3: 1. This is obtained by
Price of a Diary/ Price of a booklet = 30/10 = 3/1
We can say that the cost of the diary is three times the cost of the booklet.

Ratio,
In certain situations, comparison by division makes better sense than comparison by taking the difference. The comparison by division is known as the Ratio. Originally, it is important to remember that for comparison, the two amounts must be in the same unit. However, they should be expressed in the same unit before the ratio is taken, if they are not in the same unit. Secondly, the ratio in which amounts are taken is also important. E.g. when the price of diary is Rs. 30 and the price of booklet is Rs. 10, we get the following
Price of a Diary/ Price of a Notebook = 30/10 = 3/1
Price of a Tablet/ Price of a Diary = 10/30 = 1/3
Therefore, the order in which amounts are taken to express their ratio is important.
Another important property of ratio is we can get original ratios by multiplying or dividing the numerator and denominator by the same number.
6 4 = 6/4 = 6 *2/4 * 2 = 12/8
Properties of ratio
Two quantities can be compared only if they are in same units. Equivalent ratios can be determined by multiplying or dividing the numerator and denominator by the same number.
Ratio in simplest form
The simplest form of the ratio is when the numbers are expressed as natural numbers with no common factors between them. For example, 2: 4 can be written in the simplest form as 1: 2.
1. A ratio between two quantities of same kind and in the same units is obtained on dividing one quantity by the other and has no unit. The ratio is independent of the units used in the quantities compared.
2. The ratio must always be expressed in its simplest form or in its lowest terms.
A ratio is said to be is the simplest form or in the lowest term if two quantities of a ratio (i.e., antecedent and consequent) have no common factor (i.e. antecedent and consequent are co-prime) other than 1 (or their HCF is 1.)
Equivalent ratios,
Equivalent ratios are the ratios that are the same when we compare them. Two or more ratios can be compared with each other to check whether they are equivalent or not. For example, 1:2 and 2:4 are equivalent ratios.
Comparison of ratios
Comparison of ratios means comparing the relationship between two or more ratios. The quantitative relationship of two amounts or numbers is called ratio and when 3 or more quantities come into play, a comparison of ratios is necessary.
Check the ratios are equivalent or not
By multiplying each ratio by the second number of the other ratio, you can determine if they are equivalent.
Multiply both numbers in the first ratio by the second number of the second ratio. For example, if the ratios are 3:5 and 9:15, multiply 3 by 15 and 5 by 15 to get 45:75.
Multiply both numbers in the second ratio by the original second number of the first ratio. In this example, multiply 9 by 5 and 15 by 5 to get 45:75.
Compare the results. If the results are equal, the two ratios are equivalent. If not, they are not equivalent and the ratio with the higher first number is larger. For example, if you had started with the ratios 3:5 and 12:15, you would get 45:75 and 60:75. Since the second ratio has the higher first number, (60 is greater than 45), 12:15 is larger than 3:5.

 Param Publication
Param Publication
 ReginaTagebücher
ReginaTagebücher
