Chapter 2: Whole Numbers

Introduction

As we know, we use 1, 2, 3, 4,... when we begin to count. They come naturally when we start counting. Hence, mathematicians call the counting numbers as Natural numbers. 
    
    Predecessor and successor
    Given any natural number, you can add 1 to that number and get the next number i.e. you get its successor. The successor of 16 is 16 + 1 = 17. 
    Similarly, if we substract 1 from that number we get predecessor of that number, the predecessor of 20 is 20 – 1 = 19. 

Whole Numbers

The numbers 1, 2, 3, ...., are called natural numbers or counting numbers. Let us add one more number, i.e., zero (0), to the collection of natural numbers. Now the numbers are 0, 1, 2, 3, ..... These numbers are called whole numbers.

Properties of multiplication
    (i)    Closure Property : If a and b are whole numbers, then their product a x b = c will always be a whole number. That is whole numbers are closed under multiplication.
        For ex.     7 x 3  = 21x 6 x 8 = 48 x 3 x 0 = 0  

    (ii)    Commutative Property :  In general a x b = b x a  for all whole numbers a and b.
        Consider the following example
            2 x 3 = 3 x 2 = 6
            8 x 9 = 9 x 8 = 72

    (iii)    Associative Property : If a,b and c are whole numbers, then (a x b) x c = a x (b x c)
        That is, whole numbers have the associative property of multiplication.
        For ex.    (3 x 4) x 2 = 3 x  (4 x 2)
            12 x 2 = 3  x 8
            24 = 24

    (iv)    Multiplicative Identity : 1 x a = a x 1 = a. Hence, 1 is called the multiplicative identity for whole numbers.
        For ex.              10 x 1 = 1  x 10  = 10
                     3  x 1  = 1 x 3  = 3
                  672  x 1 = 1  x 672 = 672
                       0 x 1 = 1 x 0 = 0

Properties of division

(i)    Closure Property : If a and b are whole number , then the quotient a ÷ b need not always be a whole number. So, division in whole numbers is not closed.

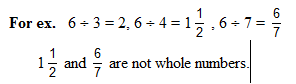
Commutative Property : If a and b are whole numbers, then a ÷ b is not equal to b ÷  a. So, the commutative property does not hold true for whole numbers.

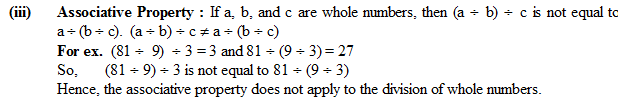
Properties Of Addition & Substraction

Properties of Addition
    (i)    Closure Property : If ‘a’ and ‘b’ are two whole numbers and their sum is c, i.e., a + b = c, 
then c  will always be a whole number. This property of a addition is called the closure property of addition.
        For ex. :  2 + 8 = 10 i.e., whole number + whole number = whole number

    (ii)    Commutative Property : If a and b are two whole numbers a + b = b + a. This property of addition, where the order of addition does not alter the sum, is called the commutative property of addition
        For ex.     3 + 4 = 7
        Also,     4 + 3 = 7
        i.e.,    3 + 4 = 4 + 3

    (iii)    Associative Property : If a, b and c are three whole numbers, then a + (b + c) = (a + b) + c. In other words, in the addition of whole numbers, the sum does not change even if the grouping is changed. This property is called the associative property of addition.
        For ex.    2 + (3 + 4) = (2 + 3) + 4 
            2 + 7 = 5 + 4
            9 = 9 

    (iv)    Additive Identity : If a is a whole number ,then  a + 0 = 0 + a = a. 
        Hence, zero is called the additive identity of the whole numbers because it maintains (or does not change) the identity (value) of the numbers during the operation of addition.
        For ex.     7 + 0 = 7 = 0 + 7

Properties of subtraction
    (i)    Closure Property : If a and b are two whole numbers, then a – b will be a whole number only if a is greater than b or a is equal to b. If a is smaller than b, then the answer will not be a whole number. Hence, subtraction is not closed under whole numbers.
        For ex.     7 – 2 = 5 is whole number 
            but 3 – 8 is not a whole number

(ii)    Commutative Property : If a and b are two distinct whole numbers, then a – b is not equal to b – a. Hence, the commutative property is not true for subtraction of whole numbers.
        For ex.     a – b ≠ b – a 
            7 – 2 ≠ 2 – 7 

    (iii)    Associative Property : If a, b and c are whole numbers, then (a – b) – c is not equal to a – (b – c). So, the associative property also does not hold true for subtraction of whole numbers
        For ex.     (12 – 4) – 3 = 8 – 3 = 5
            12 – (4 – 3) = 12 –1 = 11 
       Therefore    (12 – 4) – 3 ¹12 – (4 – 3)

The Number Line

We draw a line. Mark a point on it. Label it 0. Mark a second point to the right of 0. Label it 1.
    The distance between these points labelled as 0 and 1 is called unit distance.
    On this line, mark a point to the right of 1 and at unit distance from 1 and label it 2. In this way labelling points at unit distances as 3, 4, 5,... on the line. We can go to any whole number on the right in this manner. This is a number line for the whole numbers.

Addition on the number line
    Addition of whole numbers can be shown on the number line. Let us see the addition of 3 and 4.

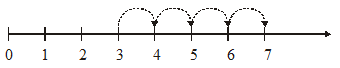
Start from 3. Since we add 4 to this number so we make 4 jumps to the right; from 3 to 4, 4 to 5, 5 to 6 and 6 to 7 as shown above. The tip of the last arrow in the fourth jump is at 7.
    The sum of 3 and 4 is 7, i.e. 3 + 4 = 7.

Subtraction on the number line
    The subtraction of two whole numbers can also be shown on the number line. Let us find 7 – 5.    

Start from 7. Since 5 is being subtracted, so move towards left with 1 jump of 1 unit. Make 5 such jumps. We reach the point 2. We get 7 – 5 = 2.

Multiplication on the number line 
    We now see the multiplication of whole numbers on the number line. Let us find 4 × 3.