1. The Ratio
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Ratio and Proportion
Ratio
A ratio is the comparison of two or more quantities of same kind using division or we can define ratio of two quantities a and b of the same kind in the same units as a fraction ![]() which is written generally as a : b (read as ‘a’ is to ‘b’). In the ratio a : b, ‘a’ is called the first term or antecedent and ‘b’ is called the second term or consequent.
which is written generally as a : b (read as ‘a’ is to ‘b’). In the ratio a : b, ‘a’ is called the first term or antecedent and ‘b’ is called the second term or consequent.
RATIO IN SIMPLEST FORM OR LOWEST TERM
A ratio is said to be in its simplest form or lowest terms when its terms do not have common factor except 1.
Note :
1. Ratio only exists between quantities of same kind :
(i) There exists no ratio between the height of a child and the weights of a child.
(ii) We cannot write a ratio between the age of a student and the marks obtained by the student.
2. To find a ratio between the quantities of same kind, quantities should be expressed in same units.
3. Ratio has no unit.
(I) Comparison of Ratio: Two ratios can be compared by converting them to like fractions. If the two fractions are equal, we say that two given ratios are equivalent.
Illustration 1
Express the ratio 36 : 81 in the simplest form.
Solution
H.C.F. of 36 and 81 is 9
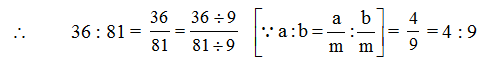
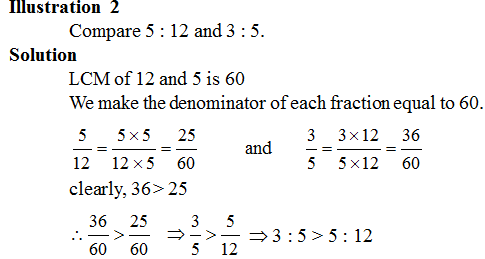
1. The Ratio
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
Chapter -8
Comparing Quantities
The Ratio
Introduction to ratio
Ratios are used to compare quantities.
Symbol ':' is used to denote ratio.
• For a ratio, the two quantities must be in the same unit. If they are not, they should be expressed in the same unit before the ratio is taken.
Example: If there are four girls and seven boys in a class, then the ratio of number of girls to number of boys is 4:7.

g. Cost of 6 pens is Rs 90. What would be the cost of 10 such pens?
Solution: Cost of 6 pens = Rs 90
Cost of 1 pen = 90 ÷ 6 = Rs 15
Hence, cost of 10 pens = 10 × 15 = Rs 150.
Application of ratios
Ratios have numerous applications in various fields on a daily basis.
- Used in finance - Current ratio, debt-equity ratio, etc.
- Used in chemistry to know the ratio of quantity of chemicals to be mixed in a chemical reaction.
- Used to solved mathematical problems involving - speed-distance-time, boat and stream problems,etc

Equivalent ratios
- By multiplying numerator and denominator of a rational number by a non zero integer, we obtain another rational number equivalent to the given rational number. These are called equivalent ratio.


Example
![]()
And
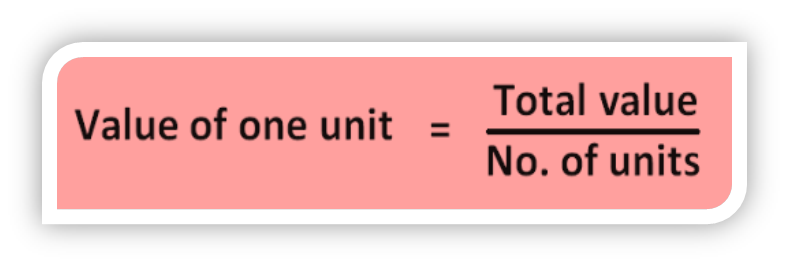
Unitary method
Unitary method is the method of finding the value of one unit (unit rate) at first and then the value of required number of units
2. Percentage
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Equivalent Ratio
A ratio obtained by multiplying or dividing the numerator and denominator of a given ratio by the same non-zero number is called an equivalent ratio. A ratio remains unchanged if both of its terms are multiplied or divided by same non zero quantity.
If n ≠ 0, then :
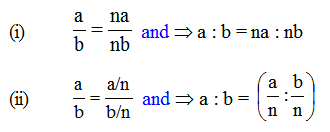

2. Percentage
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
Percentage
Introduction to percentage
Percentages are essentially fractions where the denominator is 100. To show that a number is a percent, we use the percent symbol (%) beside the number. For example, if you got 75 questions right out of 100 on a test (75/100), you would have scored 75%.
Conversion methods of percentage
Conversion of per cent into fraction
To convert a per cent into a fraction, divide it by 100 and remove the "%" sign.
![]()
Example:
(i) 37% = 37100
(ii) 22% = 22100
Note: Per cent is a fraction with a denominator of 100, and the numerator of this fraction is called Rate per cent.
2. Conversion of fraction into per cent
To convert any fraction to per cent, multiply it by 100 and put the per cent sign(%).
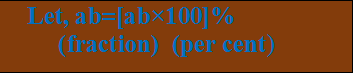
Example:
210=[210⋅100]% = 20%
Conversion of percentage into fraction
To convert the per cent into a ratio, change it to a fraction by dividing it by 100 and removing the per cent(%) sign. Finally, reduce the obtained fraction to the simplest form.
Conversion of ratio into per cent
We can convert the ratio into a percentage using the following method.
Example:
(i) a:b
=ab=[ab×100]%
Conversion of per cent into decimal
To convert the per cent to decimal, first change it to a fraction by dividing it by 1000 and remove the % sign. Then put the decimal point accordingly.
Conversion of decimal into a per cent
To convert decimal into a per cent, change it to fraction to remove decimal and then multiply it by 100 and put the % sign.
Theoretical explanation about finding a percentage
Finding a percentage of a given number:
To find the percentage of a given number, multiply the number by the require percent.
Let the number =x
Require percent =p%
Percentage of given number =p% of x
= p100 × x
Finding the original number from its percent:
Let original number =x
Require percent =p%
Obtained percentage =y
Now p% of x=y
p100×x =y
x= yp×100
![]()
Finding how much percent one quantity is of another quantity:
To find what percent of one quantity is of the other quantity if two quantities are given, we proceed as:

Percentage: Important points to remember

3. Percentage Application
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics

Illustration 9
In an examination, 96% of the candidates passed & 50 failed. How many candidates appeared ?
Solution
Let the number of candidates appeared be x
Percentage of those who passed = 96%
Percentage of those who failed = (100 – 96)% = 4 %
Number of failures = 4% of x.
∴ 4% of x = 50
![]()
Hence, the number of candidates appeared is 1250.
Illustration 10
(i) Chalk contains calcium, carbon and oxygen in the ratio 10 : 3 : 12, find the % of carbon in chalk.
(ii) If in a stick of chalk, carbon is 3g, what is the weight of the chalk stick ?

3. Percentage Application
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
Percentage Application
Percentage, Increase and decrease percentage
Percentage Increase
When comparing the increase in a quantity over a period of time, we first find the difference between the original value and the increased value. We then use this difference to find the relative increase against the original value and express it in terms of percentage. The formula for percentage increase is given by:
Percentage Decrease
When comparing the decrease in a quantity over a period of time, we first find the difference between the original value and the decreased value. We then use this difference to find the relative decrease against the original value and express it in the form of a percentage. The formula for percentage decrease is given by:
Percentage: Marks, Profit and loss- Introduction
Profit and Loss Basic Concepts
Let us learn profit and loss concepts in math. It is well explained in terms of cost price and selling price.
Profit(P)
The amount gained by selling a product with more than its cost price.
Loss(L)
The amount the seller incurs after selling the product less than its cost price is mentioned as a loss.
Cost Price (CP)
The amount paid for a product or commodity to purchase is called a cost price. Also, denoted as CP.
This cost price is further classified into two different categories:
Fixed Cost: The fixed cost is constant, it doesn’t vary under any circumstances
Variable Cost: It could vary depending as per the number of units and other factors
Selling Price (SP)
The amount for which the product is sold is called the Selling Price. It is usually denoted as SP. Also, sometimes called a sale price.
Profit and loss as a percentage
Marked Price Formula (MP)
This is basically labelled by shopkeepers to offer a discount to the customers in such a way that,
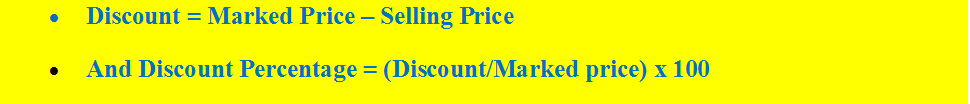
Formula for profit and loss percentage
Profit and Loss Formulas
Now let us find the profit formula and loss formula.
The profit or gain is equal to the selling price minus the cost price.
Loss is equal to cost price minus selling price.

The formula for the profit and loss percentage is:
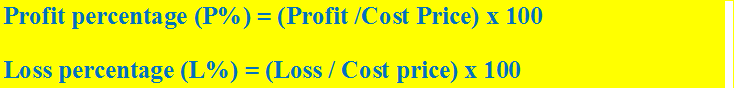
Things you should know about discount
4. Simple interest
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Percentage
The word ‘Percent’ is derived from Latin word ‘per centum’ meaning ‘per hundred’. The symbol for percent is %.
When we take 100 as the denominator of fractions, the numerator are called percentages. Per cent can also be expressed as a ratio with its second term 100 & first term equal to the given percent.

![]()
4. Simple interest
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
Simple interest
Introduction to interest
Interest is the amount of money that is paid for the use of borrowed money.
Let a person 'A' borrows some money from 'B' for a certain period of fixed time at a fixed rate, then 'A' will pay the borrowed money along with the additional money, which is called interest.
There are two types of interest:
Simple interest
Compound interest.
- Principal
- Amount
- Time
Principal (P):
The money borrowed or lend out for a certain period is called the "principal" or the "sum".
Amount (A):
The sum of the interest and principal is called the amount.
Amount (A)= Principal (P)+ Interest (I).
Time (n):
The duration of the period for which the money is borrowed is called the time.
Rate Interest per Annum (r):
If interest is payable yearly for every 100 rupees, then it is called rate per cent per annum.
Introduction to simple interest
Simple interest is a quick and easy method of calculating the interest charge on loan.
Simple interest is determined by multiplying the interest rate by the principal and by the number of days that elapse between payments.
This type of interest usually applies to automobile loans or short-term loans.
Derivation of the formula to calculate the Simple interest (I):
First, take P as the principal or sum and r% as a rate percent per annum. On every ₹100 borrowed, the interest paid is ₹r.
Therefore, on ₹P borrowed, the interest paid for one year would be =P×1×r100.
Then the interest period for two years =P×2×r100.
Then the interest period for three years =P×3× r100 and so on.
If the time period is 'n ' number of years, the formula will be I=P×n×r100.
Basic Formulae:
Amount (A) :
If the principal amount (P), and simple interest (I) are given, then we can find out the amount, by adding the principle and simple interest.

Simply rearranging both the formula as per requirement, we can find all the variants in the formula.
![]()


5. Charge given on borrowed money or simple interest
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Profit, Loss & Discount
Cost price : The money paid by the shopkeeper to buy the goods from a manufactures or a wholesale is called the cost price of the shopkeeper & it is abbreviated as C.P.
Selling price : The price at which a shopkeeper sells the goods is called the selling price of the shopkeeper, it is abbreviated is S.P.
Shopkeeper makes gain or profit if S.P. > C.P.
Profit = S.P. – C. P.
S.P. = Profit + C.P.
C.P. = S.P. – Profit
Loss = C.P. – S.P.
S.P. = C.P. – Loss
C.P. = S.P. + Loss
Gain or loss is always calculated on C.P.

Overhead Charges : Shopkeeper has to bear some additional expenses such as sales tax, labour charges, maintenance charges for the goods before they are sold. Such charges are called overhead charges. Overhead charges becomes a put of cost price.
Illustration 12
An article was purchased for M400 and sold for M336. Find the loss & loss percent.
Solution
C.P. of article = M400
S.P. of article = M336
Since S.P. < C.P., so there is a loss
Loss = C.P. – S.P.
= M(400 – 336) = M64
![]()
Hence, loss = M64
Loss % = 16%.
Illustration 13
Selling price of a toy car is M540. If the profit made by shopkeeper is 20%, what is the cost price of this toy?
Solution
![]()
Illustration 14
A fruit seller bought bananas for M40 out of them, 20 bananas were spoiled and thrown away.
He sold the remaining bananas at a profit of 10%. Find the selling price of the bananas.

Charge Given on Borrowed Money or Simple Interest
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Simple Interest
Sometimes we need to borrow money from a bank or a money lender for a specific period of time.
At the end of this period, we have to pay back the money which we had borrowed plus some additional money for using the lender’s money.
In this connection, we use the following terms.
(i) Principal : The money borrowed by a borrower from a lender is known as principal or sum.
(ii) Interest : The additional money paid by the borrower to the lender for using his money is called the interest.
(iii) Amount : The total money which the borrower pays back to the lender at the end of the specific period is called amount.
Amount = Principal + Interest
A = P + I
(iv) Rate : The interest on Rs. 100 for 1 year is known as the rate per annum.
(v) Simple Interest : If interest is calculated uniformly on the original principal throughout the loan period, it is called Simple Interest.
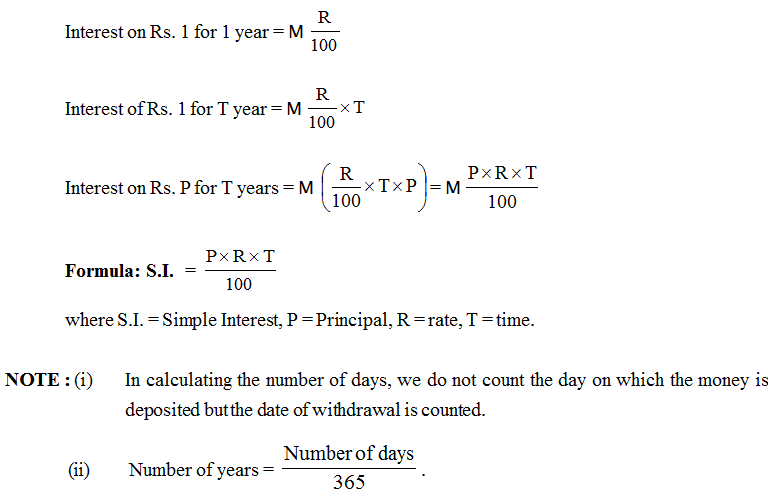
Illustration 16
Sudhir borrowed Rs. 3,00,000 at 12% per annum from a money-lender. At the end of 3 years, he cleaned the amount by paying Rs. 2,60,000 and a gold necklace. Find the cost of necklace.


 Param Publication
Param Publication
 ReginaTagebücher
ReginaTagebücher
