6. Addition and subtraction of algebraic expressions

Addition or subtraction of like terms
     The sum or difference of several like terms is another like term whose coefficient is the sum or difference of those like terms.
    Illustration 1 
        Add the following : 3xy, 10xy and 5xy.
    Solution
        The sum of the numerical coefficients of the given like terms is 3 + 10 + 5 = 18.
        Hence, 3xy + 10xy + 5xy = 18xy.

    Illustration  2
         Add the following : – 2p²q,  – 9p²q,  – 14p²q and  – 5p²q.
    Solution
        The sum of the numerical coefficients (without negative sign) is : 2 + 9 + 14 + 5 = 30
        Hence, –2p²q – 9p²q – 14p²q – 5p²q = – 30p²q.
 
    Illustration  3
         Add the following : 3x + y + 4 and 4x + 3y + 7.
    Solution    
        Horizontal Method
            (3x + y + 4) + (4x + 3y + 7)
        =     (3x + 4x) + (y + 3y) + (4 + 7)
        =     (3 + 4)x + (1 + 3)y + (4 + 7)
        =     7x + 4y + 11

                 Or

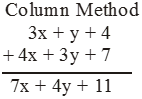
Illustration 4
         Add the following : 3x + 4y + 5z and 2x – 3y – 4z.
 Solution
        Horizontal Method
            (3x + 4y + 5z) + (2x – 3y – 4z)
        =     (3x + 2x) + (4y – 3y) + (5z – 4z)
        =     (3 + 2)x + (4 – 3)y + (5 – 4)z
        =     5x + y + z

                 Or

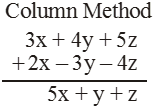
NOTE : To subtract an expression from another, we change the sign (from' + ' to ' – ' and from' – ' to ' + ') of each term of the expression to be subtracted and then add the two expressions.

Illustration 5 
        Subtract :
         (i) 3p from 7p        (ii) – 8x from 9x    (iii) – 3a from 7a    (iv) – 9b from – 2b
 Solution
        (i)     7p – 3p = (7 – 3)p = 4p
        (ii)     9x – (–8x) = 9x + 8x =(9 + 8) x = 17x
        (iii)     7a – (–3a) = 7a + 3a = (7 + 3)a = 10a
        (iv)     – 2b – (– 9b) = – 2b + 9b = (– 2 + 9)b = 7b

Illustration 6 
        What should be subtracted from 2p³ – 4p² + 5p – 6 to obtain p² – 2p + 1 ?
 Solution
        Let X denote the required expression. 
        Then, (2p³ – 4p² + 5p – 6) – X = p² – 2p + 1    
        Hence, required expression          
        X = (2p3 – 4p2 + 5p – 6) – (p2 – 2p + 1)
        X = 2p³ – 4p² + 5p – 6 – p² + 2p – 1
        X = 2p³ – 4p² – p² + 5p + 2p – 7
        X = 2p³ – 5p² + 7p – 7

NOTE : When a grouping symbol preceded by, ‘–' sign is removed or inserted, then the sign of each term of the corresponding expression is changed (from '+' to '–' and from '–'  to  '+'). 

Illustration 7 
        Simplify : 2x – {4y – (3x – 5y)}.
 Solution
        We first remove the innermost grouping symbol ( ) and then braces { }.
        Thus, we have
            2x – {4y – (3x – 5y)}
            = 2x – {4y – 3x + 5y}        [Removing ( )]
            = 2x – {9y – 3x} 
            = 2x – 9y + 3x
            = 2x + 3x – 9y
            = 5x – 9y.

Illustration 8
        Simplify and find the value of the following expression when a = 2 and b = 3 :
        4(a² + b² + 2ab) – [4(a² + b² – 2ab) – {– b³ + 4(a – 3)}]    
  Solution
        Proceeding outward from the innermost bracket,
        4(a² + b² + 2ab) – [4(a² + b² – 2ab) – {– b³ + 4(a – 3)}]
            = 4(a² + b² + 2ab) – [4(a² + b² – 2ab) – {– b³ + 4a – 12}]
            = 4a² + 4b² + 8ab – [4a² + 4b² – 8ab + b³ – 4a + 12]
            = 4a² + 4b² + 8ab – 4a² – 4b² + 8ab – b³ + 4a – 12
            = 4a² – 4a² + 4b² – 4b² + 8ab + 8ab – b³ + 4a – 12
            =  (4 – 4)a² + (4 – 4)b² + (8 + 8)ab – b³ + 4a – 12
            = 16ab – b³ +  4a – 12
        Thus va    lue of this expression for a = 2 and b = 3 is :
            16 × 2 × 3 – (3)³ + 4 × 2 – 12  = 96 – 27 + 8 – 12 = 65.

Addition and subtraction of algebraic expressions

The numeric expression refers to any record of numbers, signs of arithmetic operations and brackets, made up with meaning.

For example:
3 + 5⋅(7−4) is an numeric expression.
3+:−5 is not a numerical expression.
An algebraic expression is a record of letters, signs of arithmetic operations, numbers and brackets, made up with meaning.
For example: a²−3b is an algebraic expression.
Whenever it comes to adding algebraic terms, we add the coefficient of like terms together. i.e. coefficient of the variable with its like variable co-efficient and constant with constant.

Addition laws

1) The amount does not change from a change in the places of the terms, i.e.
 a+b=b+a

This is the translational law of addition.
2)To add the third term to the sum of two terms, we can add the sum of the second and third terms to the first term, i.e.
 (a+b)+c=a+(b+c)

1)  This is the combined law of addition.
variable coefficient with its similar variable coefficient and constant with constant except that the fact we will include the term additive inverse.

Example:
To subtract  (12a + 7) from  (30a − 2), we have to add the additive inverse of (12a+7) with (30a−2).
Additive inverse of (12a + 7) is −(12a + 7)=(−12a − 7) 
Therefore,
(30a−2)−(12a + 7)=(30a −2) + (−12a −7)=(30a −12a)+(−2 −7)=18a −9