- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
1. Congruent Line Segments : Two line segments are congruent if they are of same length.
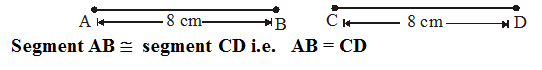
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
RHS Congruence
The triangles are said to be congruent, then the hypotenuse and one side of a right-angled triangle are respectively equal to the hypotenuse and one side of another right-angled triangle.
Example :
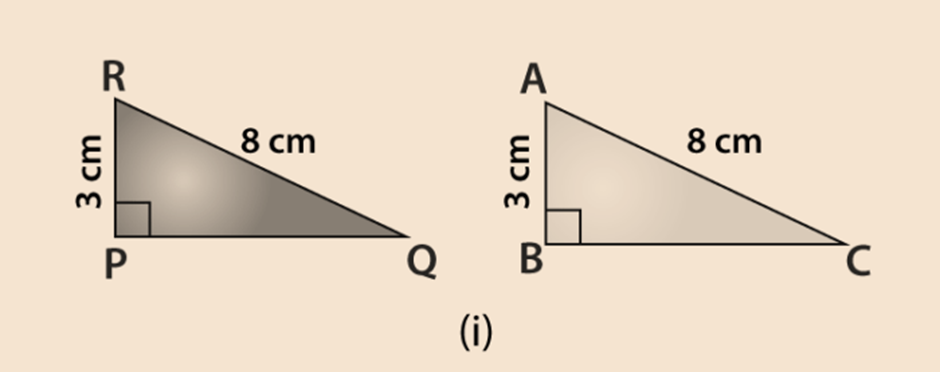
Some parts of two triangles measurements are given below. Using RHS congruence rule, examine whether the given two triangles are congruent or not. In case, if the triangles are congruent write the result in a symbolic form. For ∆ABC and ∆PQR, the measurements are given below. For triangle ABC, ∠B = 90°, AC = 8 cm, AB = 3 cm and triangle PQR, ∠P = 90°, PR = 3 cm, QR = 8 cm.
Solution :
Given : ∠B = ∠P = 90o,
Hypotenuse side AC = RQ = 8 cm and
side AB = RP = 3 cm
So, by RHS Congruence rule, the symbolic form of the congruent triangle is written as
∆ABC ≅ ∆RPQ
Example : In the following figure, AB = BC and AD = CD. Show that BD bisects AC at right angles.
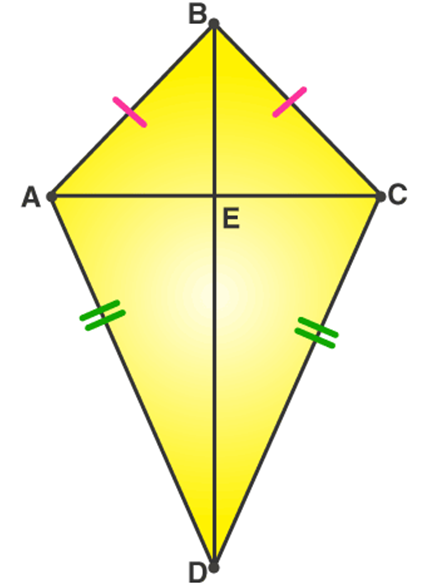
Solution: We are required to prove ∠BEA = ∠BEC = 90° and AE = EC.Consider ∆ABD and ∆CBD,AB = BC
(Given)AD = CD (Given)BD = BD
(Common)Therefore, ∆ABD ≅ ∆CBD (By SSS congruency)∠ABD = ∠CBD (CPCTC)
Now, consider ∆ABE and ∆CBE,
AB = BC (Given)
∠ABD = ∠CBD (Proved above)
BE = BE (Common)
Therefore, ∆ABE≅ ∆CBE (By SAS congruency)
∠BEA = ∠BEC (CPCTC)
And ∠BEA +∠BEC = 180° (Linear pair)
2∠BEA = 180° (∠BEA = ∠BEC)
∠BEA = 180°/2 = 90° = ∠BEC
AE = EC (CPCTC)
Hence, BD is a perpendicular bisector of AC.
In a Δ ABC, if AB = AC and ∠ B = 70°, find ∠ A.
Solution: Given: In a Δ ABC, AB = AC and ∠B = 70°
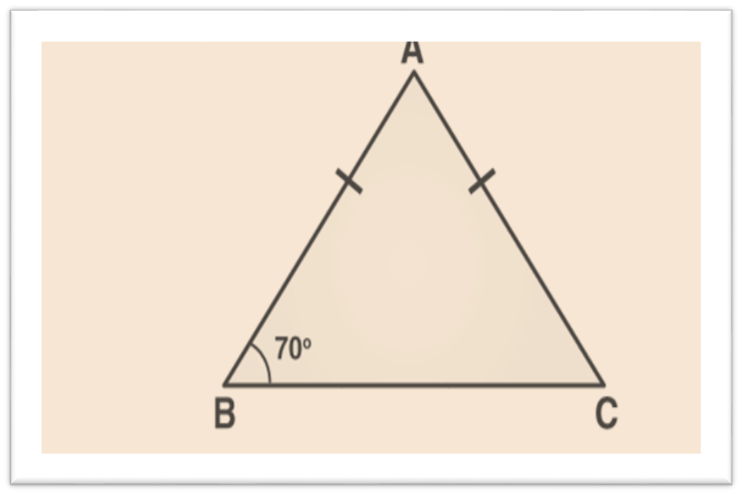
∠ B = ∠ C [Angles opposite to equal sides of a triangle are equal]
Therefore, ∠ B = ∠ C = 70°
Sum of angles in a triangle = 180°
∠ A + ∠ B + ∠ C = 180°
∠ A + 70° + 70° = 180°
∠ A = 180° – 140°
∠ A = 40°

 Param Publication
Param Publication
 ReginaTagebücher
ReginaTagebücher
