Chapter 6: The Triangle and its properties

Triangle
    A triangle is a closed figure made by three line segments. It has three vertices, three sides and three angles.

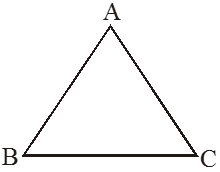
A triangle ABC is given having three vertices A, B, C and three sides AB, BC, CA and three angles are  ∠ABC,  ∠ BCA,   ∠CAB.

Classification of triangles:
1.    With respect to angles are:
    (a)     Acute-angled triangles 
    (b)     Obtuse-angled triangles 
    (c)     Right-angled traingles 

(a)     Acute-angled triangles

A triangle in which measurement of each of the three angles are less than 90°.

(b)     Obtuse-angled triangle :

A triangle in which one angle is obtuse angle i.e. greater than 90° but less then 180°.

(c)     Right-angled triangle:

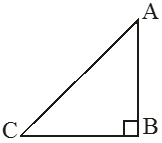
A triangle in which one angle is exactly 90°.
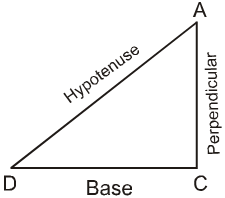
        •    The side opposite to the right angle is called the hypotenuse.
        •    The other two sides are called as the legs of the right-angled triangle (or base and perpendicular).
        •    In the given figure AC is the hypotenuse and AB and BC are the legs of  DABC.

Chapter 6  

Triangle and its properties

Median of a triangle

Median of a triangle is a line segment joining a vertex to the midpoint of the opposing side, bisecting it.

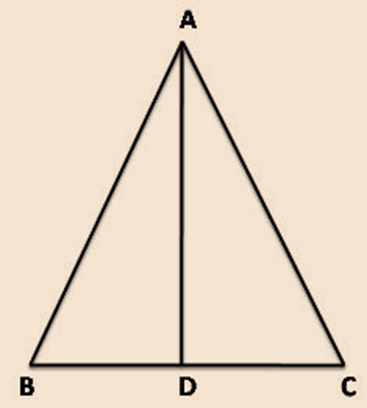
A median connects a vertex of a triangle to the mid-point of the opposite side.
In the ∆ ABC, the line segment AD joining the mid-point of BC to its opposite vertex A is called a median of the triangle.

Properties of Median of a Triangle

Every triangle has exactly three medians one from each vertex and they all intersect each other at the triangle's centroid.

• The 3 medians always meet at a single point, no matter what the shape of the triangle is.
• The point where the 3 medians meet is called the centroid of the triangle. Point O is the centroid of the triangle ABC.
• Each median of a triangle divides the triangle into two smaller triangles which have equal area.
• In fact, the 3 medians divide the triangle into 6 smaller triangles of equal area. 

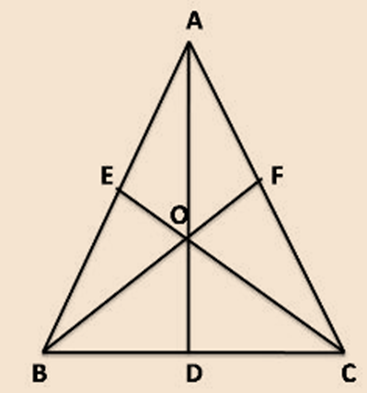
In ∆ ABC, three medians are AD, CE and BF and they are intersecting the point O which is centroid of the triangle.

Medians of a Triangle and Centroid
    Medians :-

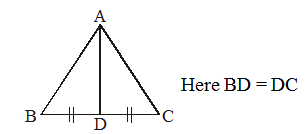
AB, BC, CA are the sides of  and AD is a line segment which intersects side BC of  at point D such that AD bisects the side BC. This line segment AD is called the median of .
A median is a line segment which connects a vertex of a triangle to the mid point of the opposite side.

Centroid :-

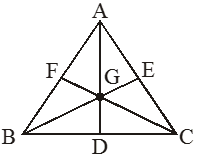
•    Centroid is the point of intersection of all three medians of a triangle.
•    In the given figure G is the centroid of 
•    A centroid of a triangle cuts the median in the ratio 2 : 1
        ⟹    AG : GD = 2 : 1

Altitude of a triangle

An altitude of a triangle is a line segment through a vertex and perpendicular to (i.e., forming a right angle with) a line containing the base (the side opposite the vertex).

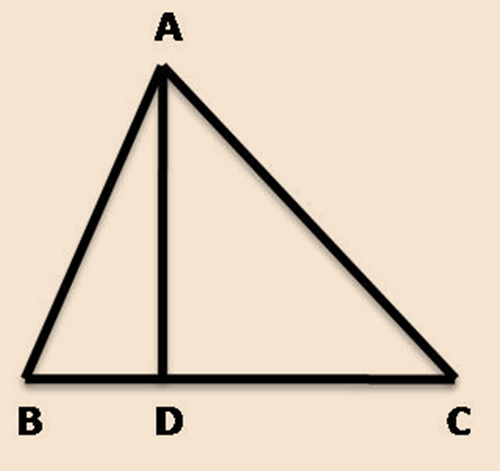
In ∆ ABC, AD is the altitude of triangle ABC.
Through each vertex, an altitude can be drawn. So, there are at most three altitudes in a triangle.
Properties of Altitudes of a Triangle

• Every triangle has 3 altitudes, one from each vertex. AE, BF and CD are the 3 altitudes of the triangle ABC.
• The altitude is the shortest distance from the vertex to its opposite side.
• The 3 altitudes always meet at a single point, no matter what the shape of the triangle is.
• The point where the 3 altitudes meet is called the ortho-centre of the triangle. Point O is the ortho-centre of the triangle ABC.
• The altitude of a triangle may lie inside or outside the triangle. 

ALTITUDES OF A TRIANGLE AND ORTHOCENTRE

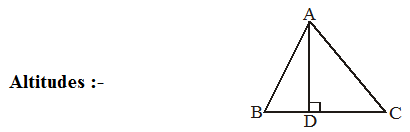
AD is a line segment which is perpendicular to the side BC of ∆ABC .This line segment AD is called as altitude of ∆

Altitude is also called as height of a triangle. In the given figure AD is the height of ∆ ABC  from vertex A to side BC.

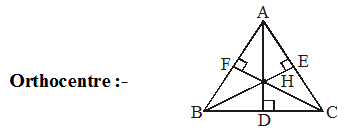
•    Orthocentre is the meeting point of all three altitudes of a triangle.
•    In the given figure H is the orthocentre of ∆ ABC.
•    In obtuse-angled triangle the orthocentre lies outside the triangle.
•    In Acute-angled triangle the orthocentre lies inside the triangle.
•    In a Right-angled triangle, the right angle lies at the vertex at which the right angle is formed.

Exterior angles of a triangle

An exterior angle of a triangle is equal to the sum of the opposite interior angles.   

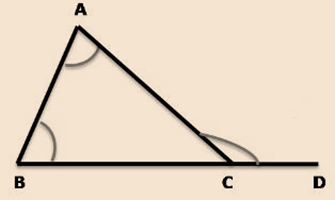
In the above figure, ∠ACD is the exterior angle of the Δ ABC.
So, ∠ACD = ∠CAB + ∠CBA
At each vertex of a triangle, an exterior angle of the triangle may be formed by extending one side of the triangle.

Exterior Angle Property of a Triangle -

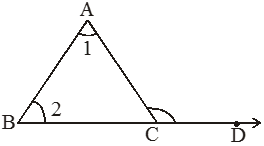
Illustration 1
        Is it possible to draw a triangle whose sides are 3 cm, 4 cm and 7 cm ?
 Solution    
        Sides of a triangle are 3 cm, 4cm, 7 cm.
        Here 3 + 4 = 7 
        and we know that sum of two sides of a triangles is always greater than the third side so it is not possible to draw a triangle whose sides are 3 cm, 4 cm and 7 cm.

 Illustration 2
         In each of the following there are three positive numbers. State if these numbers could possibly be the lengths of the sides of a triangle.
        (i) 2, 3, 4        (ii) 2.5, 1.5, 4
 Solution
        (i)     We have,
            2 + 3 > 4, 2 + 4 > 3 and 3 + 4 > 2
            That is, the sum of any two of the given numbers is greater than the third number.
            So, 2 cm, 3 cm and 4 cm can be the lengths of the sides of a triangle.
        (ii)     We have,
            2.5 + 1.5 ≯ 4.
            So, the given numbers cannot be the lengths of the sides of a triangle.

Illustration 3
         The length of two sides of a triangle are 12 cm and 15 cm. Between what two measure should the length of the third side fall ?
 Solution
         Let x cm be the length of the third side. 
        Then 12 + x > 15; 15 + x > 12  and 12 + 15 > x.
        ⇒     x > 15 – 12; x > 12 –15 and 27 > x. 
        ⇒       x > 3 ; x > – 3 and 27 > x.
        A number greater than 3 is obviously greater than – 3.
        ∴    x > 3 and 27 > x.
        Hence, x lies between 3 cm and 27 cm.

Property : Angles opposite to equal sides of a triangle are equal.
Property : Sides opposite to equal angles of a triangle are equal.
Property : In a right triangle, if a, b are the lengths of the sides and c that of the hypotenuse, then c² = a² + b².
(Hypotenuse)² = (Base)² + (Perpendicular)²

Property : If the sides of a triangle are of lengths a, b and c such that c² = a² + b², then the triangle is right angled and the side of length c is the hypotenuse.

Note : Three positive numbers a, b, c in this order are said to form a pythagorean triplet, if 
c² = a² + b². Triplets (3, 4, 5) (5, 12, 13), (8, 15, 17), (7, 24, 25) and (12, 35, 37) are some pythagorean triplets. 

 Illustration 1
        The sides of certain triangles are given below. Determine which of them are right triangles :
        (i)     a = 6 cm, b = 8 cm and c = 10 cm
        (ii)     a = 5 cm, b = 8 cm and c = 11 cm.
Solution
        (i)     Here the larger side is c = 10 cm.
            We have : a² + b² = 6² + 8² = 36 + 64 = 100 = c².
            So, the triangle with the given sides is a right triangle.
        (ii)     Here, the larger side is c = 11 cm
            Clearly, a² + b² = 25 + 64 = 89 ≠ c².
            So, the triangle with the given sides is not a right triangle.

Illustration 2
         A ladder 25 m long reaches a window of a building 20 m above the ground. Determine the distance of the foot of the ladder from the building.
  Solution
        Suppose that AB is the ladder, B is the window and CB is the building. Then, triangle ABC is a right triangle, with right angle at C.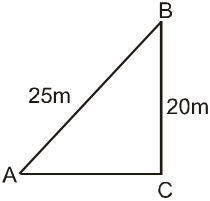                              
       ∴    AB² = AC² + BC²                               
       ⇒   25² = AC² + 20²    
       ⇒    AC² = 625 – 400 = 225    

Illustration 3
        A ladder 17 m long reaches a window which is 8 m above the ground on one side of the street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window at a height of 15 m. Find the width of the street.

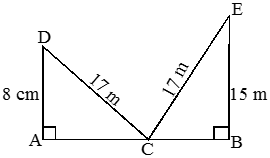
      Solution    
        Let AB be the street and C be the foot of the ladder. Let D and E be the windows at the height of 8 m and 15m respectively from the ground. 
        Then, CD and CE are the two positions of the ladder.
        In right triangle, DDAC, we have
        AC² + AD² = CD²
⇒        AC² = (CD² – AD²)
        = {(17)² – (8)²} m² = 289 – 64 = 225 m² 

In right triangle, DCBE, we have 
        CB² + BE² = CE²
  ⇒  CB² = (CE² – BE²) = {(17)² – (15)²} m² = 64 m²

Hence, width of the street = AB = (AC + CB) = (15 + 8) m = 23 m.

Illustration 4
        A tree has broken at a height of 5 m from the ground and its top touches the ground at a distance of 12m from the base of the tree. Find the original height of tree.

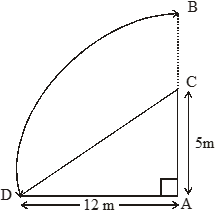
Solution
        Let AB be the tree and Let C be the point at which it broke.
        Then CB takes the position CD.
        Original height of tree i.e., AB
        i.e.    AC + BC⇒  AC + CD (∵
        i.e.     ∆ACD, using pythagoras theorm, we
            CD² = AC² + AD²
            CD² = (5)² + (12)² = 25 + 144 = 169
            CD² = 132
            CD = 13 m
        So. height of tree = AC + BC
                   = AC + CD
                   = (5+13) m
                   = 18 m
        Hence,  height of the tree = 18 m.

Apply angle sum property of a triangle

The sum of the measures of the three angles of a triangle is 180°

In Δ ABC,
∠A + ∠B + ∠C = 180°

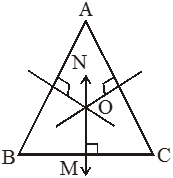
Angle Sum Property of a Triangle:
    The sum of the measures of three angles of a triangle is 180°.

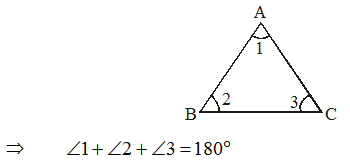
Proof of Angle Sum Property of a Triangle

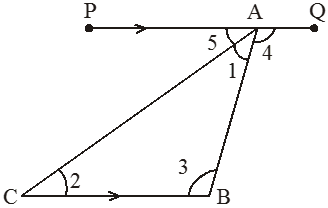
Given : A triangle ABC.
 To prove :  ∠ A +∠B +∠C = 180°
 Construction : Draw a line segment PQ through A and parallel to BC.

 Proof:    Mark the angles as indicated in the figure.

Hence, ∠ A +∠B +∠C = 180°
or sum of the angles of a triangle is 180°

ANGLE BISECTORS OF A TRIANGLE AND IN-CENTRE
    Angle Bisectors :-

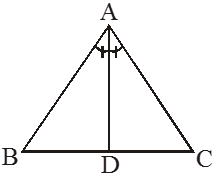
Angle bisector of a triangle is a line segment which bisect the angle and whose end points lies on the vertex and its opposite side.
    •    In the given figure, AD is the bisector of 
         So ∠BAD = ∠DAC
        Incentre    

•    In-centre is the meeting point of all three angle bisectors of a triangle.
•    In the given figure, I is the Incentre of ∆
•    In-centre always lies inside the triangle.
•    The perpendicular distance from incentre to the side of triangle is always same.
      ⇒      IP = IQ = IR
•    A circle can be drawn inside the triangle by assuming I as centre and IP as radius.

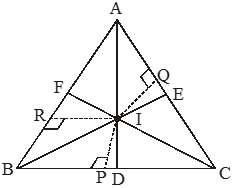
PERPENDICULAR BISECTOR AND CIRCUMCENTRE
    Perpendicular Bisector 

It is a line segment which is perpendicular to the side of a triangle and passing through the mid point of the side.
In the given figure MN is the perpendicular bisector for ∆

2.    With respect to sides are:
    (a)     Scalene triangles     (b)     Isosceles triangles     (c)     Equilateral triangles

    (a)     Scalene Triangle: A triangle in which no two sides are equal in length is called a scalene triangle.
        •     Length of all sides and measurement of all angles is different.

    (b)     Isosceles Triangle    

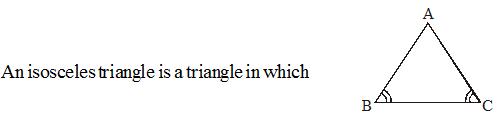
        (i)     Two sides have same length 
        (ii)     The angles opposite to the equal sides are equal.
        If in DABC, AB  = AC then ∠B = ∠C this is an isoceles triangle.
        Converse is also true 
        If in a triangle two angles are equal then sides opposite to equal angles are equal in length.
        In , if ∠B = ∠C then AB = AC.

(c)     Equilateral Triangle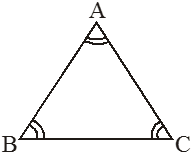  
        In an equilateral triangle
        (i)     All sides are equal in length.
        (ii)     Measurement of each angle is 60°.            
        In , if AB = BC = AC then  ∠A = ∠B =∠C = 60°
        or if  then ∠A = ∠B = ∠C= 60° AB = BC = AC

Special triangles

Two Special Triangles: Equilateral and Isosceles

A triangle in which all the three sides are of equal lengths and each angle has measure 60^o is called an equilateral triangle.

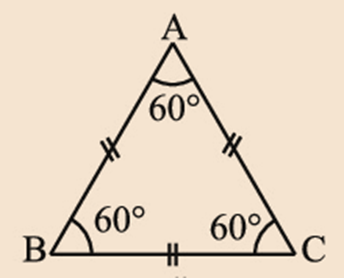
In an equilateral triangle,
AB = BC = CA
And ÐA = ÐB = ÐC = 60⁰

A triangle in which two sides are of equal lengths is called an isosceles triangle

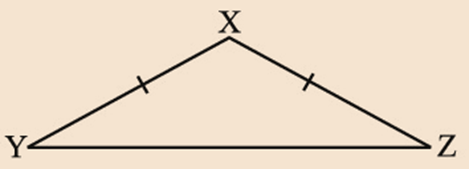
In triangle XYZ,
XY = XZ

Sum of the Lengths of Two Sides of a Triangle
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.

 In the above figure,
AB + BC > AC
Also, the difference between the lengths of any two sides of a triangle is smaller than the length of the third side.

Perimeter of a Triangle
    The sum of the lengths of the sides of a triangle is called its Perimeter.

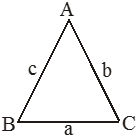
In ∆ AC = b, BC = a, AB = c then perimeter is BC + CA + AB = a + b + c 

TRIANGULAR INEQUALITY PROPERTY

The sum of the lengths of any two sides of a triangle is always greater than the third side.
        AB + BC > AC
        AB + AC > BC
        AC + BC > AB
The difference between the length of any two sides of a triangle is smaller than the length of the third side.
        AB – BC < CA
        BC – CA < AB
        CA – AB < BC

Example

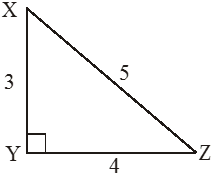
XY + YZ > XZ
        3 + 4 > 5
similary YZ + XZ > XY
        4 + 5 > 3
 similary XY + XZ > YZ
        3 + 5 > 4

Sides of a triangle

Right-Angled Triangles and Pythagoras Property

In a right angle triangle, the side opposite to the right angle is called the hypotenuse and the other two sides are known as the base and perpendicular of the right-angled triangle.   

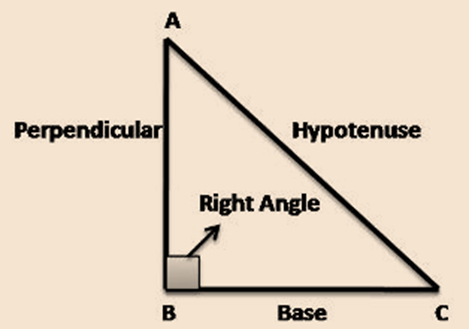
In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of base and perpendicular.
(Hypotenuse)² = (Base)² + (Perpendicular)^2]
If a triangle holds Pythagoras property, then the triangle must be right-angled.
Problem 1: PQR is a triangle, right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.

Solution:

Given: PQ = 10 cm, PR = 24 cm
Let QR be x cm.
In right angled triangle QPR,
(Hypotenuse)² = (Base)² + (Perpendicular)²                       [By Pythagoras theorem]

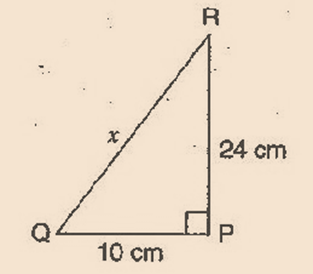
=> (QR)² = (PQ)² + (PR)²    
=> x = 10² + 24²
=> x = 100 + 576
=> x= 100 + 576 = 676
=> x = 676
=> x = √676
=> x = 26 cm
Thus, the length of QR is 26 cm.

Problem 2: A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

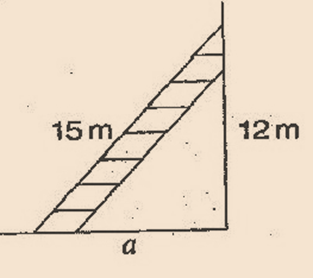
Solution:

Let AC be the ladder and A be the window.
Given: AC = 15 m, AB = 12 m, CB = a m
In right angled triangle ACB,
(Hypotenuse)² = (Base)² + (Perpendicular)2                      [By Pythagoras theorem]
=> (AC)2 = (CB)2 + (AB)2
=> 152 = a² + 122
=> 225 = a² + 144
=> a² = 225 – 144
=> a² = 81
=> a = √81
=> a = 9 cm
Thus, the distance of the foot of the ladder from the wall is 9 m.                                                                  

3.    Pythagoras Property of Right-Angled Triangle 
    In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the legs.

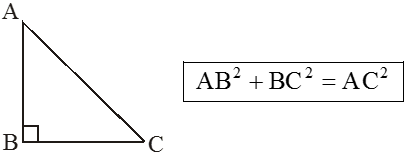
Converse of Pythagoras Theorem
    In a triangle if the square of one side is equal to the sum of the squares of the remaining two sides then the angle opposite to the first side is a right angle.
    It is clear that:-
    AC² > AB² and AC² > BC²
     ⇒   AC > AB and AC > BC.
    Hence, we can say that in right triangle the hypotenuse is the largest side.

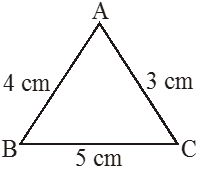
A ∆ABC is such that AB = 4 cm, AC = 3cm, BC = 5 cm and BC² = AB² + AC²  5² = 4² + 3², 
then measure of ∠A should be 90°.
Note.:    If the pythagoras property holds, the triangle must be right angled.

Pythagorian Triplets 
It is a set of three natural numbers a, b, c such that a² + b² = c². Such a set of three number it is called as Pythagorean Triplet. For example- (3, 4, 5), (5, 12, 13), (6, 8, 10) etc.