1. SSS Congruence
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Congruent figureS
Figures having same shape and size are called congruent figures.
Two figures are congruent if each is an exact image of the other. E.g. coins of M5.
Concept of superimposition
If two figures are congruent, then without bending or changing their position, if one figure is placed over the other figure and they completely overlap each other, then two figures are said to be superimposed on each other.
- Two figures are congruent if one figure superimposes the other figure.
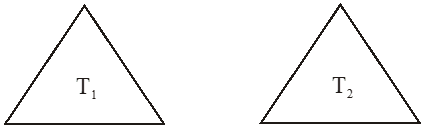
If triangle T1 superimposes triangle T2 and these two figures exactly cover each other, then they are called congruent. This method is also called superimposition method.
![]()
1. SSS Congruence
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
Chapter 7
Congruence of Triangles
Real-life examples of congruent objects
There are infinite examples of congruent objects which we see or observe in our daily life. A simple example is a pack of biscuits with all biscuits of the same size and shape if they are not broken. We can say all the biscuits are congruent.
A few more examples of congruency are:
- Earrings of the same set.
- Cigarettes in a pack.
- Wheels of a bicycle.
- Pages of a particular book.
- Your little fingers of both hands. Other fingers and thumbs are also congruent. Many of your body organs, like kidneys and lungs, are congruent. Even if a body is cut vertically from the center into two halves, both halves are congruent.
SSS Congruence
Congruence of triangles: Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure. These triangles can be slides, rotated, flipped and turned to be looked identical. If repositioned, they coincide with each other. The symbol of congruence is’ ≅’.
The meaning of congruence in Maths is when two figures are similar to each other based on their shape and size.
Congruence is the term used to define an object and its mirror image. Two objects or shapes are said to be congruent if they superimpose on each other.
The meaning of congruent in Maths is addressed to those figures and shapes that can be repositioned or flipped to coincide with the other shapes. These shapes can be reflected to coincide with similar shapes.
Congruent Triangles
A closed polygon made of three line segments forming three angles is known as a Triangle.
Two triangles are said to be congruent if their sides have the same length and angles have same measure. Thus, two triangles can be superimposed side to side and angle to angle.
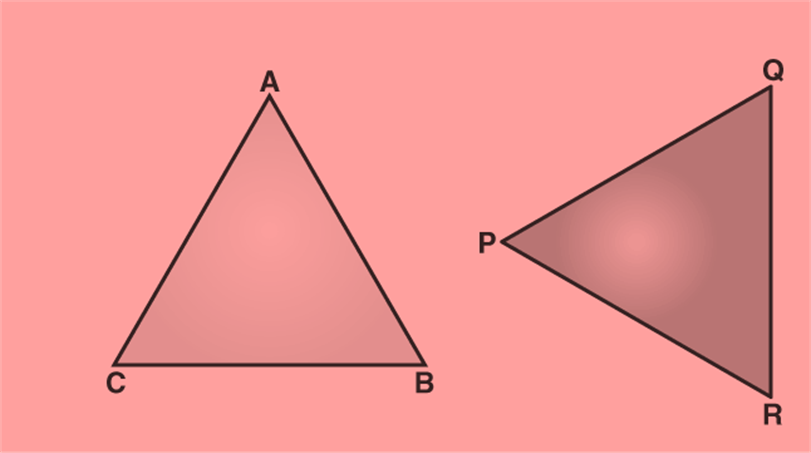
In the above figure, Δ ABC and Δ PQR are congruent triangles. This means,
Vertices: A and P, B and Q, and C and R are the same.
Sides: AB=PQ, QR= BC and AC=PR;
Angles: ∠A = ∠P, ∠B = ∠Q, and ∠C = ∠R.
SSS Congruence Rule (Side – Side – Side)
The triangles are said to be congruent if all the three sides of one triangle are equal to the three corresponding sides of another triangle
Example :
In the given triangles ABC and PQR, AB = 3.5 cm, BC = 7.1 cm, AC = 5 cm, PQ = 7.1 cm, QR = 5 cm and PR = 3.5 cm. Examine whether the given two triangles are congruent or not. If yes, then write the congruence relation in symbolic form.
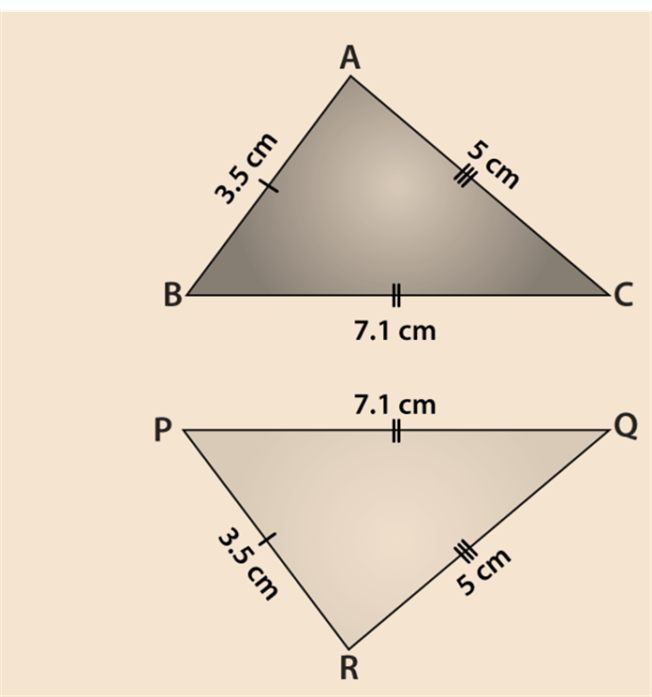
Solution :
Given : AB = PR = 3.5 cm
BC = PQ = 7.1 cm and
AC = QR = 5 cm
This shows that all the sides of one triangle are equal to all sides of the other triangle. By using SSS congruence rule, the two triangles are congruent. From the three equality relations, we can write it as
A↔R, B↔P, C↔Q
So, the congruence of triangles in symbolic form is ∆ABC ≅ ∆RPQ
2. SAS Congruence
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Different types of Congruent figures
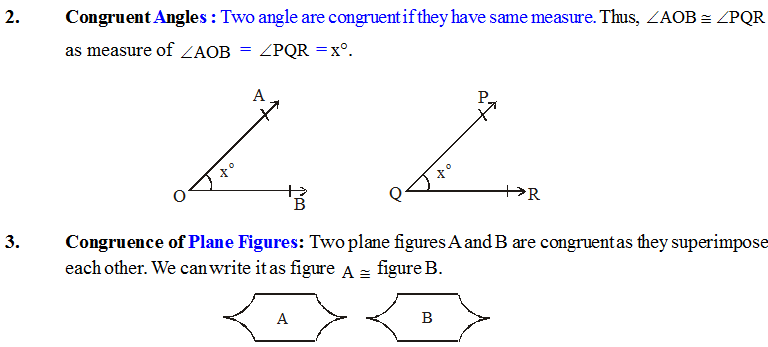
1. Congruent Line Segments : Two line segments are congruent if they are of same length.
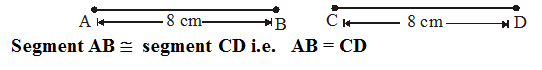
2. SAS Congruence
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
SAS Congruence
SAS Congruence Rule( Side – Angle – Side )
The triangles are said to be congruent if the correspondence, two sides and the angle included between them of a triangle are equal to two corresponding sides and the angle included between them of another triangle.
Example :
The measurements of some parts of two triangles are given below. Check whether the two triangles are congruent or not, using SAS congruence rule. Write it in symbolic form, if the triangles are congruent.
For ∆ ABC, AB = 7 cm, BC = 5 cm, ∠B = 50° and for ∆ DEF, DE = 5 cm, EF = 7 cm, ∠E = 50°
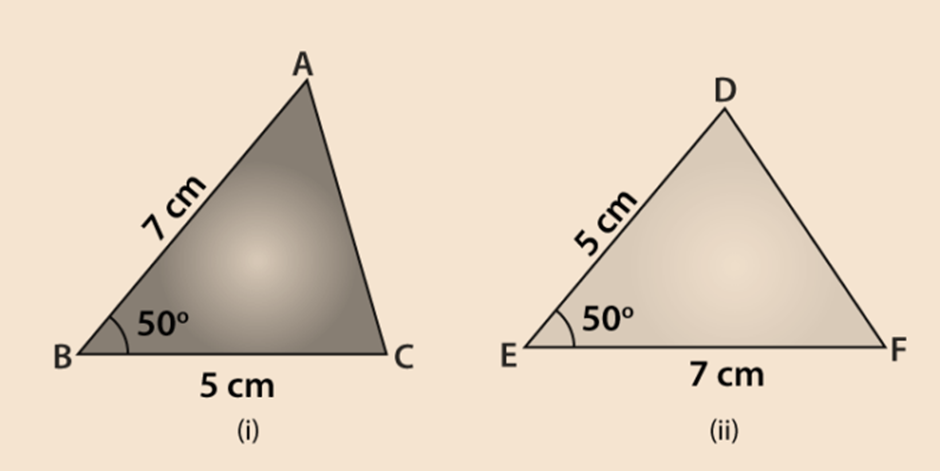
Solution :
Given: AB = EF = 7 cm,
BC = DE = 5 cm and
∠B =∠E = 50°
Also,
By using SAS congruence rule, it can be written as
∆ABC ≅ ∆FED
3. ASA Congruence
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
ASA Congruence
ASA Congruence Rule (Angle – Side – Angle )
The triangles are said to be congruent if two angles and the included side of a triangle are equal to two corresponding angles and the included side of another triangle.
Example :
Conclude that ∆AOC ≅ ∆BOD, using ASA congruence rule from the given figure.
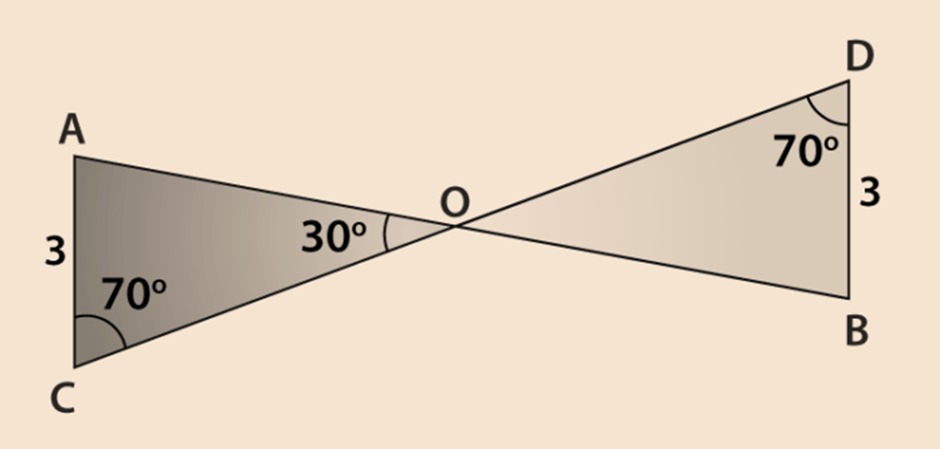
Solution :
Consider the two triangles AOC and BOD,
Given that ∠C = ∠D =70°
Also, note that ∠AOC = ∠BOD = 30° Which are vertically opposite angles
So, we can write that the angle A of triangle AOC
∆AOC = 180° – (70° + 30°) = 80° (By angle sum property of a triangle)
Similarly, for ∠B of ∆BOD = 180° – (70° + 30°) = 80°
So, we have ∠A = ∠B, AC = BD and ∠C = ∠D
Now, the side AC is between ∠A and ∠C and the side BD is between ∠B and ∠D.
So, by using ASA congruence rule, it is written as
∆AOC ≅ ∆BOD.
4. RHS Congruence
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
1. Congruent Line Segments : Two line segments are congruent if they are of same length.
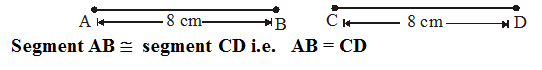
4. RHS Congruence
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
RHS Congruence
The triangles are said to be congruent, then the hypotenuse and one side of a right-angled triangle are respectively equal to the hypotenuse and one side of another right-angled triangle.
Example :
Some parts of two triangles measurements are given below. Using RHS congruence rule, examine whether the given two triangles are congruent or not. In case, if the triangles are congruent write the result in a symbolic form. For ∆ABC and ∆PQR, the measurements are given below. For triangle ABC, ∠B = 90°, AC = 8 cm, AB = 3 cm and triangle PQR, ∠P = 90°, PR = 3 cm, QR = 8 cm.
Solution :
Given : ∠B = ∠P = 90o,
Hypotenuse side AC = RQ = 8 cm and
side AB = RP = 3 cm
So, by RHS Congruence rule, the symbolic form of the congruent triangle is written as
∆ABC ≅ ∆RPQ
Example : In the following figure, AB = BC and AD = CD. Show that BD bisects AC at right angles.
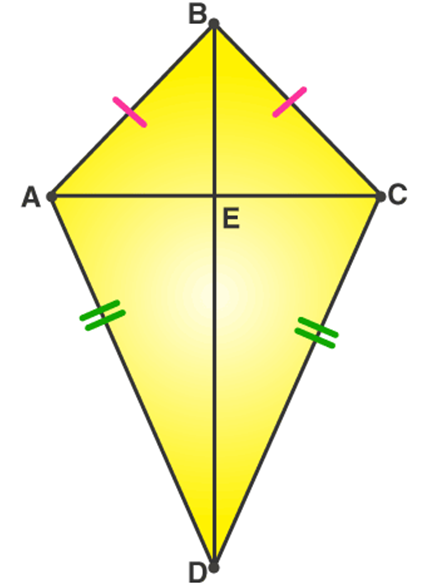
Solution: We are required to prove ∠BEA = ∠BEC = 90° and AE = EC.Consider ∆ABD and ∆CBD,AB = BC
(Given)AD = CD (Given)BD = BD
(Common)Therefore, ∆ABD ≅ ∆CBD (By SSS congruency)∠ABD = ∠CBD (CPCTC)
Now, consider ∆ABE and ∆CBE,
AB = BC (Given)
∠ABD = ∠CBD (Proved above)
BE = BE (Common)
Therefore, ∆ABE≅ ∆CBE (By SAS congruency)
∠BEA = ∠BEC (CPCTC)
And ∠BEA +∠BEC = 180° (Linear pair)
2∠BEA = 180° (∠BEA = ∠BEC)
∠BEA = 180°/2 = 90° = ∠BEC
AE = EC (CPCTC)
Hence, BD is a perpendicular bisector of AC.
In a Δ ABC, if AB = AC and ∠ B = 70°, find ∠ A.
Solution: Given: In a Δ ABC, AB = AC and ∠B = 70°
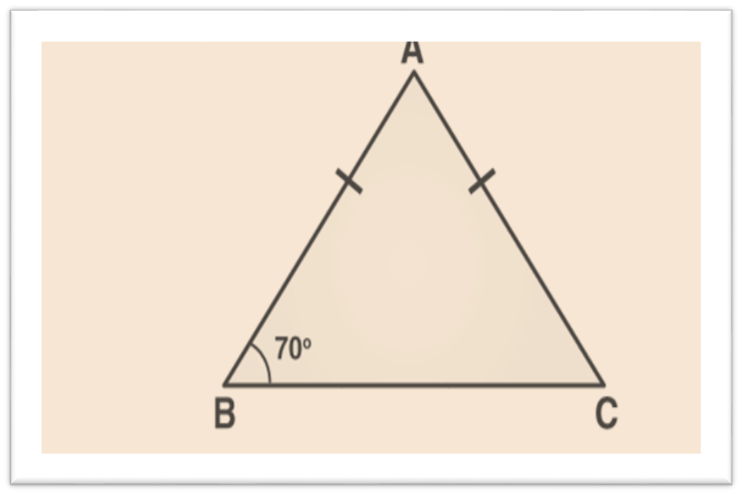
∠ B = ∠ C [Angles opposite to equal sides of a triangle are equal]
Therefore, ∠ B = ∠ C = 70°
Sum of angles in a triangle = 180°
∠ A + ∠ B + ∠ C = 180°
∠ A + 70° + 70° = 180°
∠ A = 180° – 140°
∠ A = 40°
6. Congruence among Right Angled triangles
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
CONGRUENCE OF TRIANGLES
Two triangles are congruent if pairs of corresponding sides and corresponding angles are congruent.
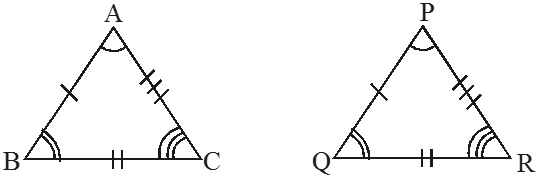
![]()
We can superimpose ∆∆ so as to cover it exactly.
During superimposing, side AB falls on side PQ, BC falls on side QR and AC falls on PR. Vertex A falls on P, B falls on Q and C fall on R. If two triangles are congruent then corresponding parts (i.e. angles and sides) that match one another are equal. Thus, in these two congruent triangles, we have;

Criteria for Congruence of Triangles
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
CONDITIONS OF CONGRUENCY OF TRIANGLES
Two triangles can be proved congruent using any of the following criteria :
I. SSS Congruency Criterion (Side-Side-Side)
If three sides of a triangle are equal to the corresponding sides of another triangle, then the two triangles are congruent by SSS congruence criterion.
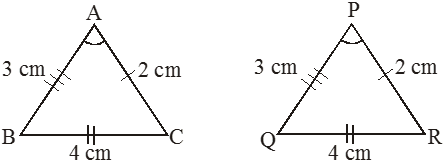
In ∆ABC and ∆PQR
AB = PQ = 3 cm
BC = QR = 4 cm
AC = PR = 2 cm
![]()
II. SAS Congruency Criterion (Side-Angle-Side)
If two triangles have two corresponding sides equal and the angle included between these sides is also equal, then the two triangles are congruent by SAS congruence criterion.
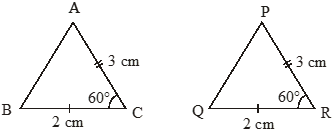

Note: Two triangles need not be congruent if the length of two sides and a non included angle (i.e. angle is not between the two given sides) of one triangle are equal to the length of two sides & a non-included angle of the other triangle
III. ASA Congruency Criterion (Angle-Side-Angle)
If two angles and the included side of one triangle are equal to the two corresponding angles and included side of another triangle, then the two triangles are congruent by ASA congruence criterion.
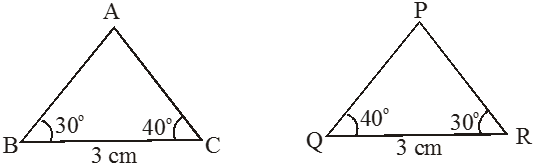

IV. AAS Congruency Criterion (Angle-Angle-Side)
If two angles and side opposite to one of the angles of one triangle are equal to two corresponding angles and side opposite to one of angles, then the two triangles are congruent by AAS congruence criterion.
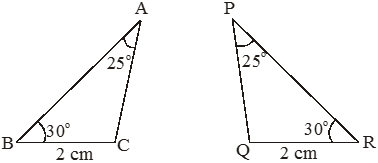

Congruence Among Right-Angled Triangles
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
V. RHS Congruency Criterion : (Right Angle-Hypotenuse-Side)
If the hypotenuse and one side of a right-angled triangle are equal to the hypotenuse and one side of another right-angled triangle, then the two triangles are congruent by RHS congruence criterion.
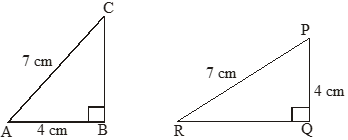

Note: Two triangles with equal corresponding angles need not be congruent. In such a correspondence, one of them can be an enlarged copy of other (They would be congruent only if they are exact copies of one another)
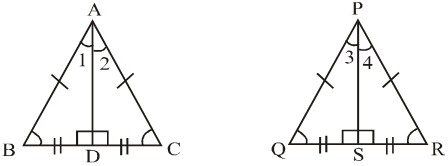
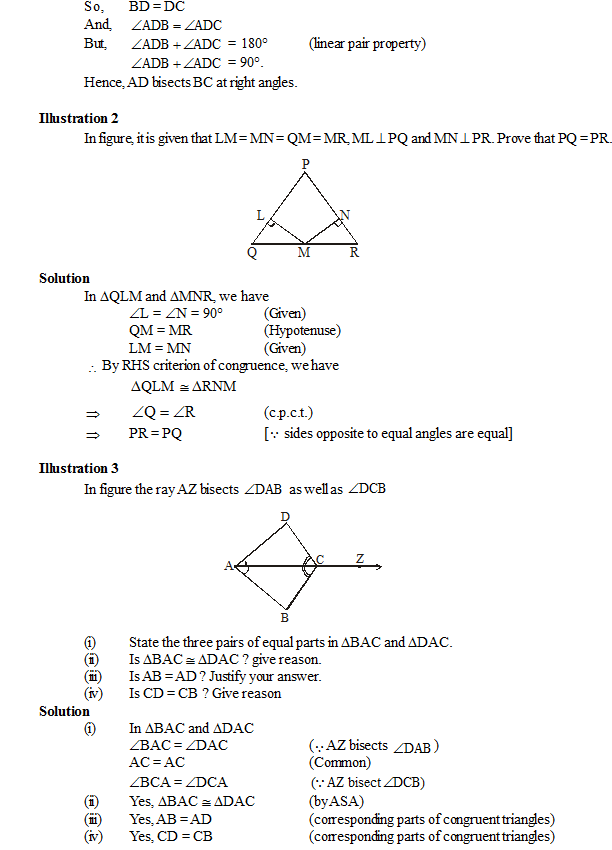
Special Properties of Isosceles and Equilateral Triangles :
1. The angles opposite to equal sides in an isosceles triangles are equal.
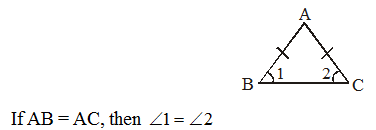
2. In an isosceles and an equilateral triangle the perpendicular drawn from the vertex to base bisects both the verticle angle and base.
(a) ABC is an Isosceles Triangle in which AB = AC
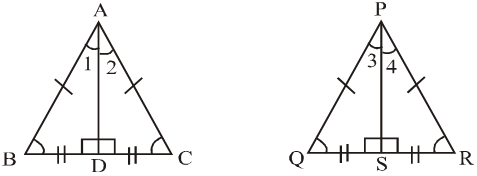
(b) PQR is and Equilateral Triangle, in which PQ = RQ = PR.


 Param Publication
Param Publication
 ReginaTagebücher
ReginaTagebücher
