- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Introduction
We have studied various types of numbers till now. These numbers are used for counting and for various other practical purposes.
Types of Numbers
1. Natural Numbers 2. Whole Numbers 3. Integers
1. Natural Numbers: All numbers which are used for counting are called natural numbers.
{1, 2, 3,......} etc. are examples of natural numbers. The set of natural numbers is denoted by N,
i.e. N = {1, 2, 3,.......}
2. Whole Numbers: All natural numbers including zero are called whole numbers. {0, 1, 2 3,....} etc. are examples of whole numbers. The set of whole numbers is denoted by W, i.e. W = {0,1,2,3......}
3 Integers: All whole numbers as well as their negatives are called integers. {...–3, –2, –1, 0, 1, 2, 3,...} are examples of integers. The set of integers is denoted by I, i.e. I = {...–3, –2, –1, 0, 1, 2, 3,...}
Important Points :
(i) All natural numbers are whole numbers but all whole numbers are not natural numbers.
(ii) Zero(0) is an integer which is neither a positive number nor a negative number.
(iii) When zero(0) is added to any other number, it gives the same number.
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
CHAPTER-1
Basic operations in Integers
Operations of integers will include the introductory computation operations( addition, deduction, addition and division). In Maths, integers are the figures that include all the positive figures, negative figures and zero, banning fragments.
Addition of Integers Positive figures When we add two positive figures, the result will always be a positive number. Hence, on adding positive figures, the direction of the move will always be to the right side.
For illustration, addition of 1 and 5( 1 +5 = 6)

Then the first number is 1, and the alternate number is 5; both are positive. First, detect 1 on a number line. also move 5 places to the right will give 6.
Negative figures When we add two negative figures, the result will always be a negative number. Hence, on adding negative figures, the direction of the move will always be to the left side.
For illustration, the addition of-2 and-3

Deduction of Integers
Positive Figures When we abate two positive figures, move to the left as far as the value of the alternate number.
For illustration, abate 5 from 2
Then the first number is 2, and the alternate number is 5; both are positive. First, detect 2 on a number line. also move 5 places to the left wing will give-3.

Negative figures When we deduct two negative figures, move to the right as far as the value of the alternate number.
For illustration, deduct -4 from-2

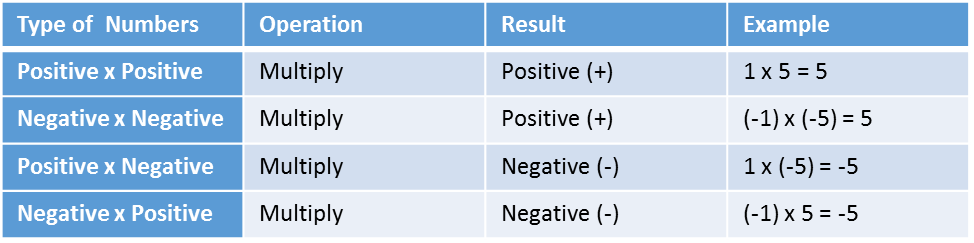
Multiplication of Integers
Multiplication of Integers
By description, multiplication is the repeated addition of numbers. But the rules for multiplication of integers are different from that of addition. It includes three possibilities. They are
Multiplication between a positive number and a negative number.
The product of two integers with like sign numbers will always be positive. This means the product of two positive numbers or two negative numbers will always be positive. While the product of a positive number and a negative number will always be negative.
Rules of Multiplication

Division of Integers
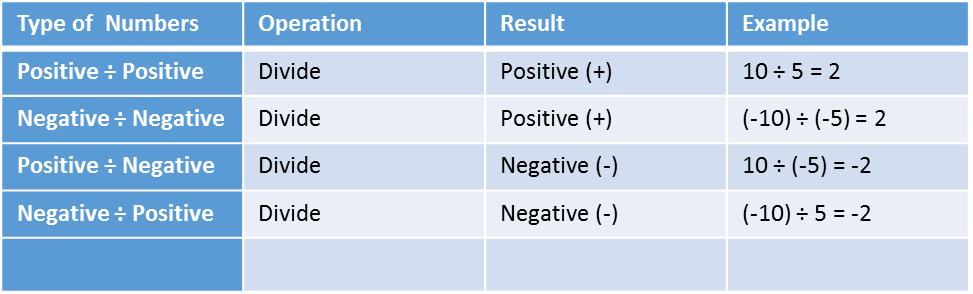
Division of Integers
Still, division is the distribution of numbers, If multiplication is totaling of numbers. Dividing integers is opposite detail of multiplication. But the rules for division of integers are same as multiplicationrules.Though, it isn't forever compulsory that the quotient will constantly be an integer.
Rule 1 The quotient of two positive integers will forever be positive.
Rule 2 The quotient of two negative numbers will forever be positive.
Rule 3 The quotient of a positive number and a negative number will forever be negative.
Rules for Dividing Integers

 Param Publication
Param Publication
 ReginaTagebücher
ReginaTagebücher
