1. Rational numbers on number line
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
INTRODUCTION
The numbers of the form p/q, where p and q are integers and q ≠0 are called rational numbers.
![]()
Note :
• All natural numbers, whole numbers, integers and fractions are rational numbers.
• A fraction is a rational number, but a rational number may or may not be a fraction.
• Zero is also a rational number.
• Every natural number is a rational number but a rational number need not be a natural number.
1. Rational numbers on number line
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
Chaper-9
Rational numbers
Rational numbers on number line
Rational numbers and integers
Natural Numbers
All positive integers like 1, 2, 3, 4……..are natural numbers.
Whole Numbers
All natural numbers including 0 are whole numbers.
Integers
All negative and positive numbers including 0 are called Integers.
Rational Numbers
Rational Numbers are the numbers that can be expressed in the form p/q where p and q are integers (q ≠ 0). It includes all natural, whole numbers, fractions and integers.
Number line or coordinate axis
rational Numbers can also be represented on a number line like integers i.e. positive rational numbers are on the right to 0 and negative rational numbers are on the left of 0.
Opposite numbers
Like integers, the additive inverse of rational numbers is also the same.
This shows that the additive inverse of 3/7 is - (3/7)
This shows that
Plotting a rational number
Basic rules of representing rational no. on number line
- If the rational no fraction is proper then, it lies between 0 and 1.
- If the rational no .fraction is improper then, we first convert it to mixed fraction and then the given rational no. lies between the whole number and next whole number.
We use following steps to represent a rational number or fraction for example, 5757 on the number line.
Step 1 − We draw a number line.
Step 2 − As the number 5757 is a positive number, it lies on the right side of zero.
Step 3 − So, after zero mark, we have 17,27,37,47,57,67,17,27,37,47,57,67, and (7777 = 1).
Step 4 − The rational number 5757 on the number line is shown as follows.
Numerator less than denominator
Let us consider 3/4 and −3/4. First, let us plot 3/4.
- Here, the numerator 3 is less than the denominator 4.
- Then the positive rational number will be between 0 and 1.
- Now, let us draw a number line and plot 1 and −1.
- Then the number 34 has to lie somewhere between 0 and 1.
- Now we divide the length between 0 and 1 into equal parts.
- The Denominator gives us the number of equal parts(4).
- It is 4, so we divide it into 4 equal parts
- The numerator tells us the number of parts starting from zero.
- Here, it is 3. So we mark the point 3 parts away from the zero as shown in the below figure
Similarly, −3/4 can be marked using the same procedure because −3/4 is the corresponding value of 34.
We know that it lies between 0 and −1. So, we divide it into four equal parts and mark 3 parts away from the zero, as shown in the below figure.
Numerator greater than denominator
Let us consider 64 and −64. First, let us plot 64.
- Here, the numerator 6 is greater than the denominator 4.
- Then, we have to convert it into a mixed fraction.
- A mixed fraction of 64 is 124.
- Now, let us draw a number line and plot 1,−1 and 2,−2.
- Then the number 124 has to lie somewhere between 1 and 2.
- Now we divide the length between 1 and 2 into equal parts.
- The Denominator gives us the number of equal parts.
- It is 4, so we divide it into 4 equal parts.
- The numerator tells us the number of parts starting from 1.
- Here, it is 2. So we mark the point 2 parts away from the 1.
Similarly, −6/4 can be marked using the same procedure because −6/4 is the corresponding value of 6/4.
We know that it lies between −1 and −2. So, we divide it into four equal parts and mark 2 parts away from the −1.
2. Rational numbers between two or more rational numbers
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Properties of Rational Numbers

2. Rational numbers between two or more rational numbers
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
Rational numbers between two or more rational numbers
Rational numbers between two rational numbers
When Denominators are the same
Step 1: Check the values on the numerators of the rational numbers
Step 2: Find by how many values, the numerators differ from each other
Step 3: Since, the denominators are the same for the two rational numbers, therefore, we can write the rational numbers between the two given rationals, in the increasing order of numerator, if the difference between the two numerators is more.
Step 4: If the difference between two numerators is less, and we need to find more rational numbers, then multiply the numerator and denominator of the given rational numbers by multiples of 10.
When Denominators are Different
Suppose we have two rational numbers with different denominators, then follow the below steps to find the rational numbers between them.
Step 1: Find the LCM of two rational numbers first.
Step 2: Multiply and divide the two rational numbers, by the value that results in the denominators equal to the obtained LCM.
Step 3: Once the denominators become the same, follow the same rules as we have discussed for the rational numbers with the same denominators.
Step 4: If the difference between two numerators is less, and we need to find more rational numbers, then multiply the numerator and denominator of the given rational numbers by multiples of 10.
Visual representation of rational numbers between two rational numbers
if we want to find more number of rational numbers between 3/ 5and 4/5. We should write the multiple of the rational numbers, that is,
3/5can be written as 30/ 50 and 4/5can be written as 40/50
From, this we can understand that an infinite (or) an uncountable number of rational numbers are present between any two rational numbers.
Using average method to find rational numbers between two rational numbers
Let us take two numbers as x and y, then
average = x + y2
Let, x and y be any two rational numbers, then we can find as many rational numbers between x and y by using the average concept as e1,e2,e3,e4,e5....etc
e1=x+y2;e2=x+e12;e3=x+e22. (e2,e3) represents the rational numbers present to the left of the average of x and y, which is to the left of e1 in the number line.
Rational numbers following a pattern
Aasha was asked to write 3 more rational numbers similar to 12,24,36,48,..... She noticed that
all these numbers surprisingly follow a pattern like, 1×22×2=24,1×32×3=36,1×42×4=48.
Since she identified the pattern in which the numbers are written, it became easy for her to write 3 more rational numbers.
It is 1×52×5=24,1×62×6=612,1×72×7=712.
3. Four basic operations on Rational numbers
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
The numbers of the form p/q, where p and q are integers and q ≠0 are called rational numbers.
![]()
Note :
• All natural numbers, whole numbers, integers and fractions are rational numbers.
• A fraction is a rational number, but a rational number may or may not be a fraction.
• Zero is also a rational number.
• Every natural number is a rational number but a rational number need not be a natural number.
EQUIVALENT RATIONAL NUMBERS
Two rational numbers are said to be equivalent if their standard forms are same.

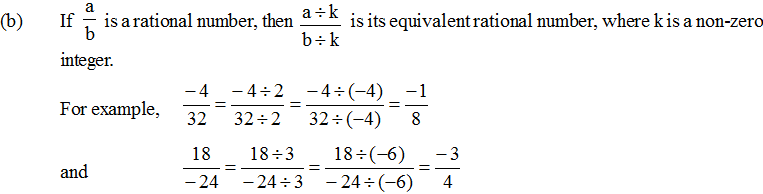
3. Four basic operations on Rational numbers
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
Four basic operations on Rational numbers
Addition of rational numbers
add all the numerators and write the common denominator. For example, add 1/8 and 3/8. Let us understand this with the help of a number line.
- On the number line, we start from 1/8.
- We will take 3 jumps toward the right as we are adding 3/8 to it. As a result, we reach point 4/8. 1/8 + 3/8 = (1 + 3)/8 = 4/8 =1/2
- Thus, 1/8 + 3/8 = 1/2.
Division of rational numbers
whole number division that the dividend is divided by the divisor. Dividend÷Divisor=Dividend/Divisor. While dividing any two numbers, we have to see how many parts of the divisor are there in the dividend.
- Step 1: Take the reciprocal of the divisor (the second rational number). 2x/9 = 9/2x
- Step 2: Multiply it to the dividend. −4x/3 × 9/2x
- Step 3: The product of these two numbers will be the solution. (−4x × 9) / (3 × 2x) = −6
Multiplication of Rational Numbers
To multiply any two rational numbers, we have to follow three simple steps. Let's multiply the following rational numbers: −2/3×(−4/5). The steps to find the solution are:
- Step 1: Multiply the numerators. (−2)×(−4)=8
- Step 2: Multiply the denominators. (3)×(5)=15
- Step 3: Reduce the resulting number to its lowest term. Since it's already in its lowest term, we can leave it as is. (−23)×(−45) = (−2)×(−4)/ (3)×(5) = 8/15
Subtraction of rational numbers
While subtracting two rational numbers on a number line, we move toward the left. Let us understand this method using an example. Subtract 1/2x−1/3x
- Step 1: Find the LCM of the denominators. LCM (2, 3) = 6.
- Step 2: Convert the numbers into their equivalents with 6 as the common denominator. 1/2x × 3/3 = 3/6x = 1/3x × 2/2 = 2/6x
- Step 3: Subtract the numbers you obtained in step 2.
4. Rational numbers in standard form
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Types of Rational Numbers
1. Positive Rational Numbers :A rational number is said to be positive if its numerator and denominator are either both positive or both negative.
![]()
2. Negative Rational Numbers : A rational number is said to be negative if its numerator and denominator are such that one of them is a positive integer and the other is a negative integer.
![]()
5. Comparison of rational numbers
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Representation of rational numbers on number line
Draw a straight line. Take a point O on it. Call it 0 (zero). Set off equal distances on its right as well as on the left of 0. Such a distance is known as a units length. Clearly, the points A, B, C, D, E represent the integers 1, 2, 3, 4, 5 respectively and the points A', B', C', D', E' represent the integers –1, –2, –3, –4, –5 respectively.
![]()
Thus, we may represent any integer by a point on the number line. Clearly, every positive integer lies to the right of O and every negative integer lies to the left of O.
Illustration 2
![]()
Solution:
Draw a line, take a point O on it, let it represent 0.
![]()
From O, set off unit distances OA, AB and BC to the right of O. Clearly, the points A, B and C represent the integers 1, 2 and 3 respectively. Now, take 2 units OA and AB, and divide the third unit BC into 5 equal parts. Take 3 parts out of these 5 parts to reach at a point P. Then the point P represents the rational number ![]()
![]()
Again, from O, set off unit distances to the left. Let these segments be OA’, A’ B’, B’C’, etc. Then, clearly the points A’, B’ and C’ represent the integers –1,–2,–3 respectively.
![]()
Take 2 full unit lengths to the left of O. Divide the third unit B’C’ into 5 equal parts. Take 3 parts out of these 5 parts to reach a point P’.
Then, the point P’ represents the rational number ![]()
Thus, we can represent every rational number by a point on the number line.
6. Rational numbers between two rational numbers
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
SIMPLEST (LOWEST) OR STANDARD FORM OF A RATIONAL NUMBER

7. Operations on rational numbers
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Comparing two rational numbers
In order to compare any two rational numbers, we can use the following steps :
Step I Obtain the given rational numbers.
Step II Write the given rational numbers so that their denominators are positive.
Step III Find the LCM of the positive denominators of the rational numbers obtained in step II.
Step IV Express each rational number (obtained in step II) with the LCM (obtained in step III) as common denominator.
Step V Compare the numerators of rational numbers obtained in step IV. The number having greater numerator is the greater rational number.
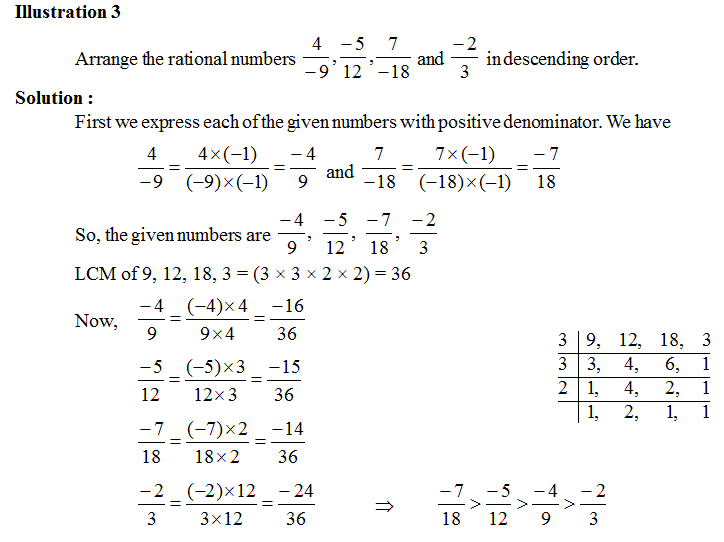
Rational Numbers Between Two Rational Numbers
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
RATIONAL NUMBERS BETWEEN TWO RATIONAL NUMBERS

By using this method, you can insert as many rational numbers as you want between two rational numbers.
Note: (i) There exist infinite rational numbers between two given rational numbers.
(ii) Between two successive integers the number of integers is 0.
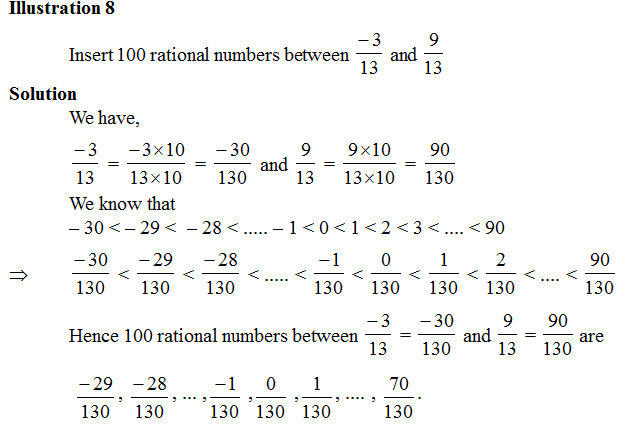
Operations on Rational Numbers
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Basic mathematical Operations on Rational numbers
1. Addition of rational numbers
Suppose we have to add two given rational numbers. First convert each of them into a rational number with a positive denominator.
Case I : When Denominators of Given Numbers are Equal :
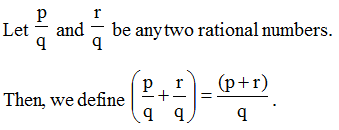
Thus, in order to add two rational numbers with the same denominator, we simply add their numerators and divide the sum by the common denominator.
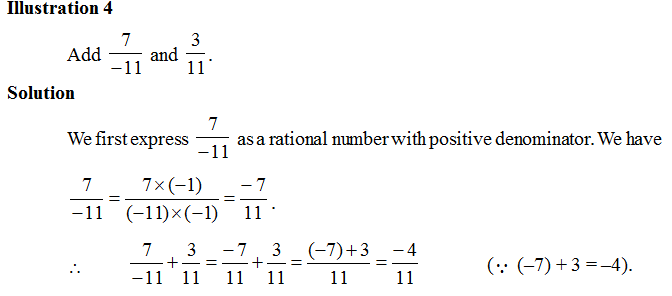
Case II : When Denominators of Given Numbers are Unequal :
Step 1 Taken the LCM of the denominators of the given rational numbers.
Step 2 Express each of the given rational numbers with the above LCM as the common denominator.
Step 3. Now, add the numbers as shown in above example.
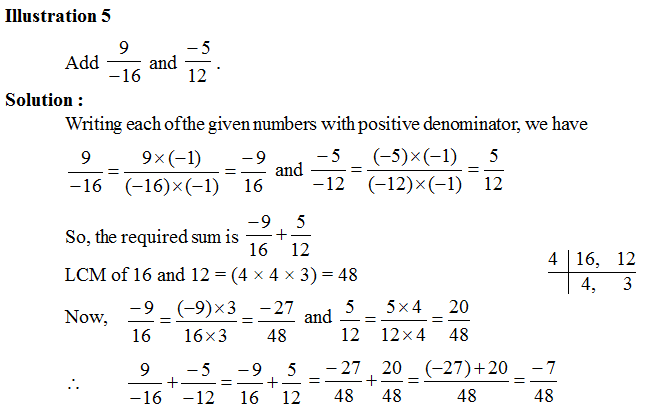
2. Subtraction of rational numbers
Subtraction is the inverse process of addition, i.e. in subtraction we add the additive inverse of a number.
Hence, additive inverse of a rational number is negative of that rational number.
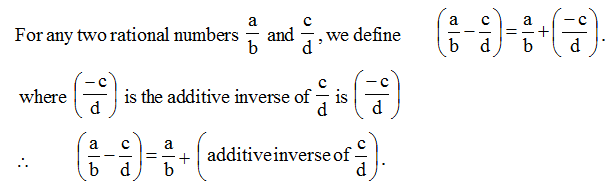

4. Division of rational numbers
We know that division is the inverse of multiplication. So to divide a rational number by another rational number is the same as multiplying the first number by the multiplicative inverse (reciprocal) of the second number.
![]()


 Param Publication
Param Publication
 ReginaTagebücher
ReginaTagebücher
