4. Apply angle sum property of a triangle

Exterior Angle Property of a Triangle -

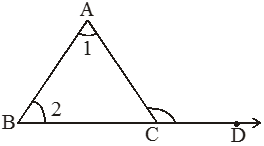
Illustration 1
        Is it possible to draw a triangle whose sides are 3 cm, 4 cm and 7 cm ?
 Solution    
        Sides of a triangle are 3 cm, 4cm, 7 cm.
        Here 3 + 4 = 7 
        and we know that sum of two sides of a triangles is always greater than the third side so it is not possible to draw a triangle whose sides are 3 cm, 4 cm and 7 cm.

 Illustration 2
         In each of the following there are three positive numbers. State if these numbers could possibly be the lengths of the sides of a triangle.
        (i) 2, 3, 4        (ii) 2.5, 1.5, 4
 Solution
        (i)     We have,
            2 + 3 > 4, 2 + 4 > 3 and 3 + 4 > 2
            That is, the sum of any two of the given numbers is greater than the third number.
            So, 2 cm, 3 cm and 4 cm can be the lengths of the sides of a triangle.
        (ii)     We have,
            2.5 + 1.5 ≯ 4.
            So, the given numbers cannot be the lengths of the sides of a triangle.

Illustration 3
         The length of two sides of a triangle are 12 cm and 15 cm. Between what two measure should the length of the third side fall ?
 Solution
         Let x cm be the length of the third side. 
        Then 12 + x > 15; 15 + x > 12  and 12 + 15 > x.
        ⇒     x > 15 – 12; x > 12 –15 and 27 > x. 
        ⇒       x > 3 ; x > – 3 and 27 > x.
        A number greater than 3 is obviously greater than – 3.
        ∴    x > 3 and 27 > x.
        Hence, x lies between 3 cm and 27 cm.

Property : Angles opposite to equal sides of a triangle are equal.
Property : Sides opposite to equal angles of a triangle are equal.
Property : In a right triangle, if a, b are the lengths of the sides and c that of the hypotenuse, then c² = a² + b².
(Hypotenuse)² = (Base)² + (Perpendicular)²

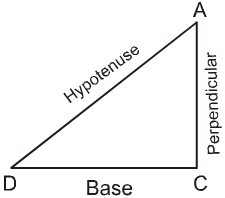
Property : If the sides of a triangle are of lengths a, b and c such that c² = a² + b², then the triangle is right angled and the side of length c is the hypotenuse.

Note : Three positive numbers a, b, c in this order are said to form a pythagorean triplet, if 
c² = a² + b². Triplets (3, 4, 5) (5, 12, 13), (8, 15, 17), (7, 24, 25) and (12, 35, 37) are some pythagorean triplets. 

 Illustration 1
        The sides of certain triangles are given below. Determine which of them are right triangles :
        (i)     a = 6 cm, b = 8 cm and c = 10 cm
        (ii)     a = 5 cm, b = 8 cm and c = 11 cm.
Solution
        (i)     Here the larger side is c = 10 cm.
            We have : a² + b² = 6² + 8² = 36 + 64 = 100 = c².
            So, the triangle with the given sides is a right triangle.
        (ii)     Here, the larger side is c = 11 cm
            Clearly, a² + b² = 25 + 64 = 89 ≠ c².
            So, the triangle with the given sides is not a right triangle.

Illustration 2
         A ladder 25 m long reaches a window of a building 20 m above the ground. Determine the distance of the foot of the ladder from the building.
  Solution
        Suppose that AB is the ladder, B is the window and CB is the building. Then, triangle ABC is a right triangle, with right angle at C.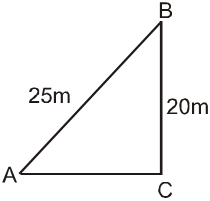                              
       ∴    AB² = AC² + BC²                               
       ⇒   25² = AC² + 20²    
       ⇒    AC² = 625 – 400 = 225    

Illustration 3
        A ladder 17 m long reaches a window which is 8 m above the ground on one side of the street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window at a height of 15 m. Find the width of the street.

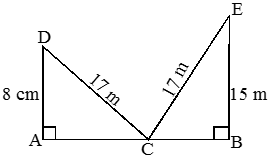
      Solution    
        Let AB be the street and C be the foot of the ladder. Let D and E be the windows at the height of 8 m and 15m respectively from the ground. 
        Then, CD and CE are the two positions of the ladder.
        In right triangle, DDAC, we have
        AC² + AD² = CD²
⇒        AC² = (CD² – AD²)
        = {(17)² – (8)²} m² = 289 – 64 = 225 m² 

In right triangle, DCBE, we have 
        CB² + BE² = CE²
  ⇒  CB² = (CE² – BE²) = {(17)² – (15)²} m² = 64 m²

Hence, width of the street = AB = (AC + CB) = (15 + 8) m = 23 m.

Illustration 4
        A tree has broken at a height of 5 m from the ground and its top touches the ground at a distance of 12m from the base of the tree. Find the original height of tree.

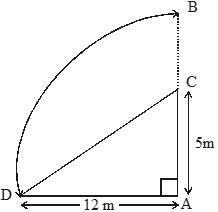
Solution
        Let AB be the tree and Let C be the point at which it broke.
        Then CB takes the position CD.
        Original height of tree i.e., AB
        i.e.    AC + BC⇒  AC + CD (∵
        i.e.     ∆ACD, using pythagoras theorm, we
            CD² = AC² + AD²
            CD² = (5)² + (12)² = 25 + 144 = 169
            CD² = 132
            CD = 13 m
        So. height of tree = AC + BC
                   = AC + CD
                   = (5+13) m
                   = 18 m
        Hence,  height of the tree = 18 m.

 

Apply angle sum property of a triangle

The sum of the measures of the three angles of a triangle is 180°

 

In Δ ABC,
∠A + ∠B + ∠C = 180°