- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
The numbers of the form p/q, where p and q are integers and q ≠0 are called rational numbers.
![]()
Note :
• All natural numbers, whole numbers, integers and fractions are rational numbers.
• A fraction is a rational number, but a rational number may or may not be a fraction.
• Zero is also a rational number.
• Every natural number is a rational number but a rational number need not be a natural number.
EQUIVALENT RATIONAL NUMBERS
Two rational numbers are said to be equivalent if their standard forms are same.

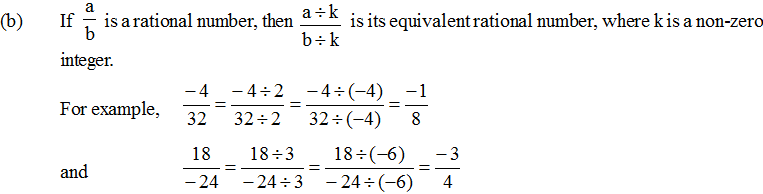
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
Four basic operations on Rational numbers
Addition of rational numbers
add all the numerators and write the common denominator. For example, add 1/8 and 3/8. Let us understand this with the help of a number line.
- On the number line, we start from 1/8.
- We will take 3 jumps toward the right as we are adding 3/8 to it. As a result, we reach point 4/8. 1/8 + 3/8 = (1 + 3)/8 = 4/8 =1/2
- Thus, 1/8 + 3/8 = 1/2.
Division of rational numbers
whole number division that the dividend is divided by the divisor. Dividend÷Divisor=Dividend/Divisor. While dividing any two numbers, we have to see how many parts of the divisor are there in the dividend.
- Step 1: Take the reciprocal of the divisor (the second rational number). 2x/9 = 9/2x
- Step 2: Multiply it to the dividend. −4x/3 × 9/2x
- Step 3: The product of these two numbers will be the solution. (−4x × 9) / (3 × 2x) = −6
Multiplication of Rational Numbers
To multiply any two rational numbers, we have to follow three simple steps. Let's multiply the following rational numbers: −2/3×(−4/5). The steps to find the solution are:
- Step 1: Multiply the numerators. (−2)×(−4)=8
- Step 2: Multiply the denominators. (3)×(5)=15
- Step 3: Reduce the resulting number to its lowest term. Since it's already in its lowest term, we can leave it as is. (−23)×(−45) = (−2)×(−4)/ (3)×(5) = 8/15
Subtraction of rational numbers
While subtracting two rational numbers on a number line, we move toward the left. Let us understand this method using an example. Subtract 1/2x−1/3x
- Step 1: Find the LCM of the denominators. LCM (2, 3) = 6.
- Step 2: Convert the numbers into their equivalents with 6 as the common denominator. 1/2x × 3/3 = 3/6x = 1/3x × 2/2 = 2/6x
- Step 3: Subtract the numbers you obtained in step 2.

 Param Publication
Param Publication
 ReginaTagebücher
ReginaTagebücher
