2. Altitude of a triangle

Medians of a Triangle and Centroid
    Medians :-

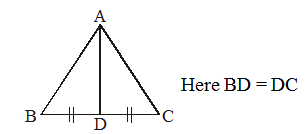
AB, BC, CA are the sides of  and AD is a line segment which intersects side BC of  at point D such that AD bisects the side BC. This line segment AD is called the median of .
A median is a line segment which connects a vertex of a triangle to the mid point of the opposite side.

Centroid :-

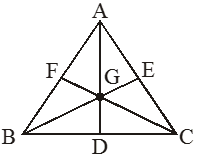
•    Centroid is the point of intersection of all three medians of a triangle.
•    In the given figure G is the centroid of 
•    A centroid of a triangle cuts the median in the ratio 2 : 1
        ⟹    AG : GD = 2 : 1

Altitude of a triangle

An altitude of a triangle is a line segment through a vertex and perpendicular to (i.e., forming a right angle with) a line containing the base (the side opposite the vertex).

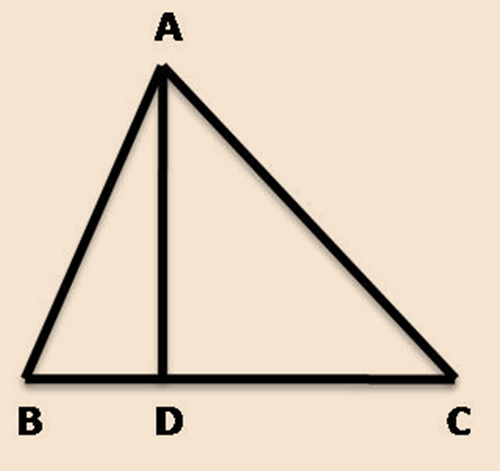
In ∆ ABC, AD is the altitude of triangle ABC.
Through each vertex, an altitude can be drawn. So, there are at most three altitudes in a triangle.
Properties of Altitudes of a Triangle

• Every triangle has 3 altitudes, one from each vertex. AE, BF and CD are the 3 altitudes of the triangle ABC.
• The altitude is the shortest distance from the vertex to its opposite side.
• The 3 altitudes always meet at a single point, no matter what the shape of the triangle is.
• The point where the 3 altitudes meet is called the ortho-centre of the triangle. Point O is the ortho-centre of the triangle ABC.
• The altitude of a triangle may lie inside or outside the triangle.