Chapter 1: Integers

Introduction
    We have studied various types of numbers till now. These numbers are used for counting and for various other practical purposes.

Types of Numbers 
    1.     Natural Numbers    2.     Whole Numbers     3.     Integers

1.    Natural Numbers: All numbers which are used for counting are called natural numbers. 
      {1, 2, 3,......} etc. are examples of natural numbers. The set of natural numbers is denoted by N, 
      i.e. N = {1, 2, 3,.......}

2.    Whole Numbers: All natural numbers including zero are called whole numbers. {0, 1, 2 3,....} etc. are examples of whole numbers. The set of whole numbers is denoted by W, i.e. W = {0,1,2,3......}

3    Integers: All whole numbers as well as their negatives are called integers. {...–3, –2, –1, 0, 1, 2, 3,...} are examples of integers. The set of integers is denoted by I, i.e. I = {...–3, –2, –1, 0, 1, 2, 3,...}

    Important Points : 
    (i)     All natural numbers are whole numbers but all whole numbers are not natural numbers.
    (ii)     Zero(0) is an integer which is neither a positive number nor a negative number.
    (iii)     When zero(0)  is added to any other number, it gives the same number.

                  CHAPTER-1

Basic operations in Integers

Operations of integers will include the introductory computation operations( addition, deduction, addition and division). In Maths, integers are the figures that include all the positive figures, negative figures and zero, banning fragments.
Addition of Integers Positive figures When we add two positive figures, the result will always be a positive number. Hence, on adding positive figures, the direction of the move will always be to the right side.
For illustration, addition of 1 and 5( 1 +5 = 6)

Then the first number is 1, and the alternate number is 5; both are positive. First, detect 1 on a number line. also move 5 places to the right will give 6.
Negative figures When we add two negative figures, the result will always be a negative number. Hence, on adding negative figures, the direction of the move will always be to the left side.
For illustration, the addition of-2 and-3

Deduction of Integers
Positive Figures When we abate two positive figures, move to the left as far as the value of the alternate number.
For illustration, abate 5 from 2
Then the first number is 2, and the alternate number is 5; both are positive. First, detect 2 on a number line. also move 5 places to the left wing will give-3.

Negative figures When we deduct  two negative figures, move to the right as far as the value of the alternate number.
For illustration, deduct -4 from-2

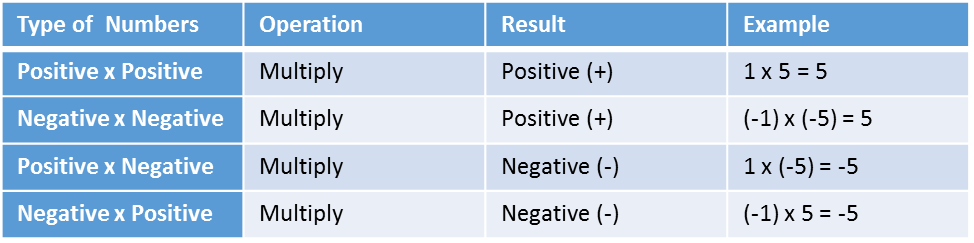
Multiplication of Integers

Multiplication of Integers

 By description, multiplication is the repeated addition of numbers. But the rules for multiplication of integers are different from that of addition. It includes three possibilities. They are

 Multiplication between a positive number and a negative number.

 The product of two integers with like sign numbers will always be positive. This means the product of two positive numbers or two negative numbers will always be positive. While the product of a positive number and a negative number   will always be negative.

Rules of Multiplication

Division of Integers

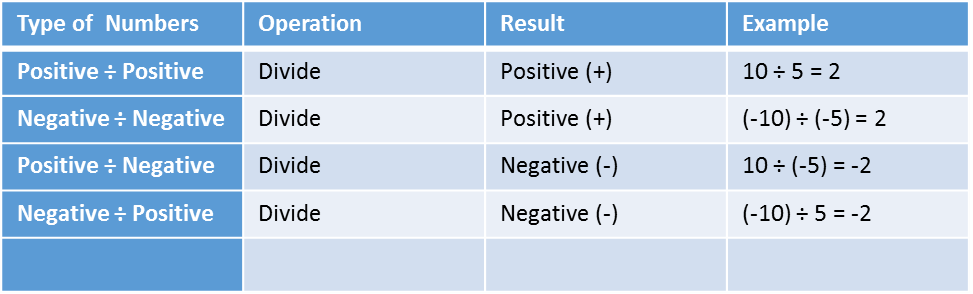
Division of Integers

 Still, division is the distribution of numbers, If multiplication is totaling of numbers. Dividing integers is opposite detail of multiplication. But the rules for division of integers are same as multiplicationrules.Though, it isn't forever compulsory that the quotient will constantly be an integer.

  Rule 1 The quotient of two positive integers will forever be positive.

 Rule 2 The quotient of two negative numbers will forever be positive.

 Rule 3 The quotient of a positive number and a negative number will forever be negative.

Rules for Dividing Integers

Properties of Integers

Integers have 5 main properties of operation which are

Closure Property
Associative Property
Commutative Property
Distributive Property
Identity Property

Properties of Addition on Integers
 (i)    Closure property of Addition : Sum of two integers is always an integer. (In general, for any two integers a and b, a + b is an integer).
        Ex.    2 + 3 = 5         (2, 3 and 5 all are integers)
            –2 + 3 = 1         (–2, 3 and 1, all are integers)
            2 + (–3) = –1        (2, -3 and –1, all are integers)
            –2 + (–3) = –5        (–2, –3 and –5, all are integers)    

(ii)    Commutative law of Addition: According to this law, if ‘a’ and ‘b’ are two integers then a + b = b + a.
         Ex.    2 + (–3) = (–3) + 2 = –1

(iii)    Associative law of Addition: Accroding to this law, if ‘a’, ‘b’ and ‘c’ are integers, then (a + b) + c = a + (b + c)
         Ex.    (2 + 5) + (–7) = 2 + (5 + –7) = 0 

(iv)    Existance of Additive Identity: For any integer ‘a’, we have a + 0 = 0 + a = a.  Zero (0) is called the additive identity for integers.
         Ex.    –2 + 0 = 0 + (–2) = –2

Properties of Subtraction on Integers :
(i)    Closure property for Subtraction : If ‘a’, and ‘b’ are any two integers then (a – b) will always be an integer.
        Ex.    12 – 9 = 3 (Where 12, 9 and 3 are all integers)

(ii)    Commutative Property for subtraction : Subtraction of integers is not commutative i.e. if ‘a’ and ‘b’ are two integers then a – b≠ b – a. 
        Ex.    2 – 3 ¹ 3 – 2

(iii)    Associative property for Subtraction of Integers : Subtraction of integers is not associative i.e. (a – b) – c ≠ a – (b – c). For exmaple if 2, –3 and 5 are three integers then 
        [(2 – (–3)] –5 = 0 and 2 – [(–3) –5] = 10
        hence [2 – (–3)] –5 ¹ 2 –[(–3) –5]

Multiplication of Integers:    
    (i)    Rule for multiplication between integers of opposite sign - When integers with opposite signs are multiplied, the result will be the product of the integers with negative sign on the product. In general for any two positive integers a and b we can say, a             a x (- b) = (- a) x b = - (a x b)
        Ex.    – 4 x 5 = –(4 x 5) = –20
            4 x –5 = –(4 x 5) = –20     

(ii)    Rule for multiplication between integers of same sign - When integers with same sign are multiplied, the result will be the product of integers with positive sign on the product. In general, for any two positive integers a and b,  (- a) x (- b) = a x b
        Ex.    –5 × –4 = 20
                 5 × 4 = 20
        (a)    The product of two negative integers is a Positive integer.
                Ex.    (-4) x (-7) = 28

        (b)    The product of three negative integers is a Negative integer.
                Ex.    (-4) x (-7) x (-1) = -28

        (c)    The product of four negative integers is a Positive integer.
                Ex.    (-4) x (-7) x (-1) x (-2) = 56    

Properties of Multiplication of Integers :
    (i)    Closure property for Multiplication : The product of two integers is always an integer. a x b is an integer, for all Integers a and b.
           Ex.    7 × 9 = 63    (7, 9 and 63 are all integers)
                  –7 × 9 = –63    (–7, 9 and –63 are all integers)
                   7 × –9 = –63    (7, –9 and –63 are all integers)
                –7 ×–9 = 63    (–7, –9 and 63 are all integers) 

(ii)    Commutative law for multiplication of Integers : For any two integers a and b, the commutative law holds true i.e., a × b = b ×a.
         Ex.    –2 × 3 = 3 × –2 = –6

(iii)    Associative law for multiplication of Integers : For any three integers a, b and c, the associative law holds true i.e. (a x b) x c = a × (b × c). If a = –2, b = –3 and c = 4, then (–2 × –3) × 4 = –2 × (–3 × 4) = 24.

(iv)    Distributive law of Multiplication over addition : For any three integers a, b and c, the distributive law holds true i.e., a × ( b + c) = a × b + a × c. 
        If a = 5, b = –3 & c = –7 then 5 × (–3 + –7) = 5 × –3 + 5 × –7 = –50

(v)    Existance of Multiplicative Identity : For every integer a, we have a × 1 = 1 x a = a. 
        Where ‘1’ is the multiplicative identity. 
        Ex.    –5 × 1 = 1 × –5 = –5

(vi)  Existance of multiplicative Inverse : For every non-zero integer x, there exists a multiplicative 
       

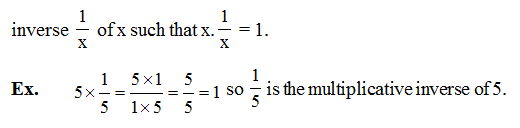
(vii)    Property of Zero: In general, for every integer a, we have a × 0 = 0 × a = 0

Division of Integers
    Rules for determining the sign, on the quotient obtained after division of two integers, are the same as those for multiplication of integers.

BODMAS Rule: Tells the order in which simplification has to be done. The order is: bracket, of, division, multiplication, addition and subtraction.
    The order of removing bracket is:
    (a)     ‘-’ called vinculam (1^st)
    (b)     ( ) called the common brackets (2^nd)
    (c)     { } called the braces (3^rd)
    (d)     [ ] called rectangular brackets (4^th) 

Properties for Division of Integers
    (i)    Closure property of division of Integers : If ‘a’ and ‘b’ integers, then (a ÷ b)  may not necessarily always be an integer ex. if a = –5 and b = 10 then 

       which is not an integer.

(ii)    Commutative property for division of two integers : For any two integers ‘a’ and ‘b’ the commutative property does not hold true. i.e. a ÷ b ≠ b ÷ a. For example if a = 2 and b = –4 then 2 ÷ (–4)≠(–4) ÷ 2.
(iii)    Associative Property for division : The associative property does not hold true for division of integers.

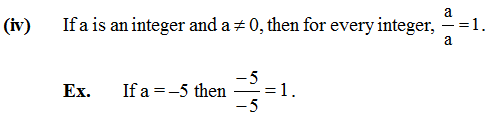
(v)    For every integer a, a ÷  1 = a. For example, if a = –10 then –10 ÷   1 = –10.
(vi)    For every integer a, we have a ÷  0 is not defined.
(vii)   For three non zero integers a, b and c, if a > b, then a ¸ c > b ÷ c if c is positive and a÷ c < b ÷  c if c is negative.
         For example : Consider three integers a = 30 b = –20 and c = 10. where a > b
        then    a  ÷  c = 30 ÷  10 = 3  which is greater than
                  b  ÷  c = 20 ÷  10 = –2 
        But when c = –10 a ÷  c = 30 ÷  (–10) = –3 which is less than b ÷  c = –20 ÷  (–10) = 2