Chapter 12: Algebraic Expressions

Various definitions and concepts
    Literals : The letters which are used to represent numbers are called literal numbers or literals. In 2xy, x & y are the literals.
    Literal numbers obey all the rules (and signs) of addition, subtraction, multiplication and division of numbers along with the properties of these operations. a × b = ab, 2 × a = 2a, 1 × a = a, x × 3 = 3x and a × a × a × ......× 15 times = a¹⁵. 
    In a⁵, 5 is called the index or exponent and a is called the base.

    Constant :  A term of the expression having no literal factor is called a constant term.

    (i)     In the binomial expression 5x + 7, the constant term is 7. In short, a symbol having a fixed numerical value is called a constant.

Variable : A symbol which takes various numerical values is called a variable.

Algebraic expression : A combination of constants and variables connected by the signs of fundamental operations of addition, subtraction, multiplication and division is called an algebraic expression.

Chapter -12

Algebraic expressions

Introduction to algebraic expressions

Algebra is the branch of mathematics that deals with the methods of finding the unknown values by using the variables and constants in the algebraic expression.
Algebraic expressions:
Combine variables and constants using the mathematical operations addition and subtraction to construct algebraic expressions.
Terms are either variables, numbers or variables multiplied together with numbers. An algebraic operation like addition and subtraction separates terms.

Variable: A variable is a symbol for an unknown value. It is usually denoted in a letter like x, y, a, b.

The number of terms: The total number of terms is known as the number of terms of a given expression.

Constant: A number which stands alone without any variables is known as constant.

Coefficient: A co-efficient can either be a numerical factor or an algebraic factor or product of both that is a number used to multiply a variable.

E.g. Kathir went to a shop to buy chocolate. He gave to shop keeper ₹50 and the shopkeeper gave him 10 chocolates.Now can you find the cost of one chocolate?

Let x be the cost of one chocolate. Then,

 x ×10=50x = 5010 = 5.

Therefore the cost of one chocolate is ₹5.

 Types of algebraic expressions
 An algebraic expression is called a monomial, a binomial, a trinomial, a quadrinomial according as it contains one term, two terms, three terms and four terms respectively. 

Types of algebraic expressions. Monomials

A product of numbers, variables and their exponents is called a monomial.            

A monomial is in a standard form, if first there is a constant (numerical) factor, and then variable factors in alphabetical order. If there are several variable factors with the same base, you multiply them, thus you get one factor for each variable.

A monomial is in a standard form, if:
 •   every product of the same variables is written as one variable with an exponent
am⋅ an=am+n;
• A constant factor (or the monomial coefficient) is written as the first term of a monomial.
The standard form of the monomial (6xy²⋅(−2)x3y) is −12x4y³ 
A constant factor of a standard form of a monomial is called the monomial coefficient.
Monomials that have the like products of the variable terms, even if the terms' order is different, are called similar monomials.
If similar monomials have the like coefficients, then these monomials are called mutually equal monomials.
Similar monomials are the monomials that have the like products of the variable terms, even if the terms' order is different.

To add or subtract monomials, the following steps must be followed:
1) add or subtract monomial coefficients; 
2) do not change the variable factors.

When multiplying or dividing a monomial by a number, the coefficient of a given monomial is multiplied or divided, but the variable factors remain the same.

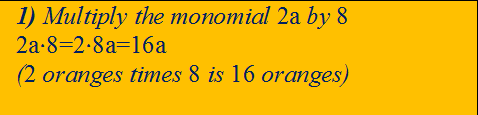
2) Divide the monomial 14b by 7 
14b:7=(14:7)b=2b
(if 14 bananas are divided equally between 7 people, each person will have 2 bananas)

3) Divide the monomial c by 10  
c:10=(1:10)c=110c=0,1c
(1 lemon divided by 10 is 1 tenth of a lemon)

Types of algebraic expressions. Binomials

Any algebraic expression with two terms is called a binomial expression. a binomial expression has only two terms. This is the reason why it is called a binomial (prefix 'bi' stands for 'two').
Degree in an algebraic expression is the sum of the exponents of the variables in the expression.
Example: 7xy²−3y²z  here

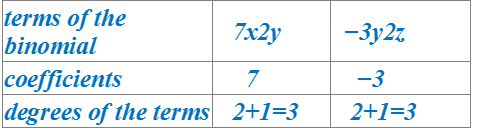
When multiplying or dividing a monomial by a number, multiply or divide only its coefficient.

Example:

6x⋅5=30x;−0,5zy⋅2=−zy;4x²:2=2x²
A binomial is an algebraic sum of monomials.

Example:

3x+2y;4xy−6y²
When multiplying or dividing a binomial by a number, each term is multiplied or divided.

Like terms : The terms having the same literal factors are called like or similar terms.
In the algebraic expression 12a² – 15b² + b² –17a² + 8ab + 9, we have, 12a² and –17a² as like terms and also – 15b² and b² are like terms. 

Unlike terms :  The terms not having same literal factors are called unlike or dissimilar terms.

In the algebraic expression 3p²q + 5pq² – 7pq – 9qp², 5pq² and –7pq are unlike terms.

Types of algebraic expressions. Trinomials

A trinomial algebraic expression is an algebraic expression that has three terms.
The prefix 'tri' in 'trinomial' stands for 3 terms.
To add two trinomials, you must:
 1) remove the brackets (without changing the signs, because the “+” sign is in front of the brackets);
2) add the like terms.

Example:
Add trinomials: 

(−5x³+3y−5y²)+(8x³+5y²−2y)

1) Remove the brackets:
(−5x³+3y−5y²)+(8x³+5y²−2y)==−5x³+3y−5y²+8x³+5y²−2y.

2) Find the like terms and add:
−5x³¯¯¯¯¯¯¯¯+3y−5y²+8x³¯¯¯¯¯¯¯¯+5y²−2y=3x³+3y¯¯¯¯¯¯−5y²+5y²−2y¯¯¯¯¯¯=3x³+y.
To multiply a trinomial by a trinomial, you need to multiply each term of one trinomial by each terms of another trinomial and add the resulting products. 
(a+b+c)⋅ (d+e+f)==a⋅d + a⋅e +a⋅f +b⋅d +b⋅e +b⋅f +c⋅d +c⋅e +c⋅f = ad + ae + af + bd + be + bf + cd + ce + cf

To subtract two trinomials , you must:

1) remove the brackets and change the signs of the trinomials that are preceded by the sign "−" to the opposite;

2) combine the like terms of the trinomials.

Example:

Let us calculate the difference of trinomials (7x²+3x−2) and −2x²+2x+3

1) Write down the difference of the trinomials and remove the brackets, taking the signs before the brackets into account:
(7x²+3x−2)−(−2x²+2x+3)=7x²+3x−2+2x²−2x−3

2) Find the like terms:
7x²¯¯¯¯¯+3x¯¯¯¯¯¯¯¯−2 +2x²¯¯¯¯¯−2x¯¯¯¯¯¯¯¯−3

3) Combine the like terms:
7x²¯¯¯¯¯+3x¯¯¯¯¯¯¯¯¯¯¯¯−2+2x²¯¯¯¯¯¯¯¯−2x¯¯¯¯¯¯¯¯¯¯¯¯−3=(7+2)x²+(3−2)x−2−3=9x²+1x−5

4) If the coefficient of a term is 1, then usually we do not write it:
9x²+1x−5=9x²+x−5

Polynomial
    A polynomial is an algebraic expression with one or more terms.
    For example : 6x, x³ + 3x² + 9x + 7, 3x² – 4xy + 7y² etc. are all polynomials.   

Degree of polynomial
    The degree of a polynomial of one variable is the highest power of the variable in the given polynomial. For example P(x) = 2x³ + 3x² – 6x + 4. The highest power of x in all terms of polynomial is 3. 
    Hence, the degree of the polynomial is 3.  
    We can classify polynomial according to its degree.
    (i)     Constant polynomial : Polynomial having degree zero is known as constant polynomial. 

(ii)     Linear polynomial : Polynomial having degree one is known as linear polynomial. 
        For ex : 2x – 5, x + 3.
(iii)   Quadratic polynomial : Polynomial having degree two is known as quadratic polynomial. 
        For ex :  x² + 1, 7x², x² + 2x – 1.
(iv)   Cubic polynomial : Polynomial having degree three is known as cubic polynomial. 
        For ex :  7x³ + 5x² + 1, x³ – x + 1.
(v)   Biquadratic polynomial : Polynomial having degree four is known as biquadratic polynomial. 
        For ex : x⁴ + 1, x⁴ + x² + 1.

Factors : Each term in an algebraic expression is a product of one or more number(s) and/or literal number(s).

These number(s) and/or literal number(s) are known as the factors of that term.
    (i)     In the binomial 8ab + 3c, 8ab and 3c are two terms. In the term 8ab, 8, a and b are its factors. Clearly, number 8 is the numerical factor, and a and b are literal factors.
    (ii)    In the binomial expression – ab – 5, the term – ab has – 1 as the numerical factor while a and b are literal factors.

Coefficient : In a term of an algebraic expression any of the factors with the sign of the term is called the coefficient of the product of the factors.
Consider the term – 5ab in the binomial – 5ab + 7. The coefficient of a in the term – 5ab is – 5b, the coefficient of b is – 5a and the coefficient of ab is – 5.

Types of algebraic expressions. Polynomials

Polynomial (poly - 'many', nomial - 'term').

 When an algebraic expression has one or many terms, then that expression is called a polynomial expression.
In some cases, polynomial multiplication can be performed easier when using the abridged multiplication formulas.

You need to remember 3 formulas:

1) The square of the sum of two expressions:
(a+b)²=a²+2ab+b²

2) The square of the difference of two expressions:
(a−b)²=a²−2ab+b²

3)  The difference of squares of two expressions:
(a−b)(a+b)=a²−b²

Addition or subtraction of like terms
     The sum or difference of several like terms is another like term whose coefficient is the sum or difference of those like terms.
    Illustration 1 
        Add the following : 3xy, 10xy and 5xy.
    Solution
        The sum of the numerical coefficients of the given like terms is 3 + 10 + 5 = 18.
        Hence, 3xy + 10xy + 5xy = 18xy.

    Illustration  2
         Add the following : – 2p²q,  – 9p²q,  – 14p²q and  – 5p²q.
    Solution
        The sum of the numerical coefficients (without negative sign) is : 2 + 9 + 14 + 5 = 30
        Hence, –2p²q – 9p²q – 14p²q – 5p²q = – 30p²q.
 
    Illustration  3
         Add the following : 3x + y + 4 and 4x + 3y + 7.
    Solution    
        Horizontal Method
            (3x + y + 4) + (4x + 3y + 7)
        =     (3x + 4x) + (y + 3y) + (4 + 7)
        =     (3 + 4)x + (1 + 3)y + (4 + 7)
        =     7x + 4y + 11

                 Or

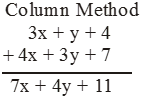
Illustration 4
         Add the following : 3x + 4y + 5z and 2x – 3y – 4z.
 Solution
        Horizontal Method
            (3x + 4y + 5z) + (2x – 3y – 4z)
        =     (3x + 2x) + (4y – 3y) + (5z – 4z)
        =     (3 + 2)x + (4 – 3)y + (5 – 4)z
        =     5x + y + z

                 Or

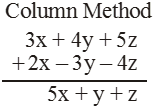
NOTE : To subtract an expression from another, we change the sign (from' + ' to ' – ' and from' – ' to ' + ') of each term of the expression to be subtracted and then add the two expressions.

Illustration 5 
        Subtract :
         (i) 3p from 7p        (ii) – 8x from 9x    (iii) – 3a from 7a    (iv) – 9b from – 2b
 Solution
        (i)     7p – 3p = (7 – 3)p = 4p
        (ii)     9x – (–8x) = 9x + 8x =(9 + 8) x = 17x
        (iii)     7a – (–3a) = 7a + 3a = (7 + 3)a = 10a
        (iv)     – 2b – (– 9b) = – 2b + 9b = (– 2 + 9)b = 7b

Illustration 6 
        What should be subtracted from 2p³ – 4p² + 5p – 6 to obtain p² – 2p + 1 ?
 Solution
        Let X denote the required expression. 
        Then, (2p³ – 4p² + 5p – 6) – X = p² – 2p + 1    
        Hence, required expression          
        X = (2p3 – 4p2 + 5p – 6) – (p2 – 2p + 1)
        X = 2p³ – 4p² + 5p – 6 – p² + 2p – 1
        X = 2p³ – 4p² – p² + 5p + 2p – 7
        X = 2p³ – 5p² + 7p – 7

NOTE : When a grouping symbol preceded by, ‘–' sign is removed or inserted, then the sign of each term of the corresponding expression is changed (from '+' to '–' and from '–'  to  '+'). 

Illustration 7 
        Simplify : 2x – {4y – (3x – 5y)}.
 Solution
        We first remove the innermost grouping symbol ( ) and then braces { }.
        Thus, we have
            2x – {4y – (3x – 5y)}
            = 2x – {4y – 3x + 5y}        [Removing ( )]
            = 2x – {9y – 3x} 
            = 2x – 9y + 3x
            = 2x + 3x – 9y
            = 5x – 9y.

Illustration 8
        Simplify and find the value of the following expression when a = 2 and b = 3 :
        4(a² + b² + 2ab) – [4(a² + b² – 2ab) – {– b³ + 4(a – 3)}]    
  Solution
        Proceeding outward from the innermost bracket,
        4(a² + b² + 2ab) – [4(a² + b² – 2ab) – {– b³ + 4(a – 3)}]
            = 4(a² + b² + 2ab) – [4(a² + b² – 2ab) – {– b³ + 4a – 12}]
            = 4a² + 4b² + 8ab – [4a² + 4b² – 8ab + b³ – 4a + 12]
            = 4a² + 4b² + 8ab – 4a² – 4b² + 8ab – b³ + 4a – 12
            = 4a² – 4a² + 4b² – 4b² + 8ab + 8ab – b³ + 4a – 12
            =  (4 – 4)a² + (4 – 4)b² + (8 + 8)ab – b³ + 4a – 12
            = 16ab – b³ +  4a – 12
        Thus va    lue of this expression for a = 2 and b = 3 is :
            16 × 2 × 3 – (3)³ + 4 × 2 – 12  = 96 – 27 + 8 – 12 = 65.

Addition and subtraction of algebraic expressions

The numeric expression refers to any record of numbers, signs of arithmetic operations and brackets, made up with meaning.

For example:
3 + 5⋅(7−4) is an numeric expression.
3+:−5 is not a numerical expression.
An algebraic expression is a record of letters, signs of arithmetic operations, numbers and brackets, made up with meaning.
For example: a²−3b is an algebraic expression.
Whenever it comes to adding algebraic terms, we add the coefficient of like terms together. i.e. coefficient of the variable with its like variable co-efficient and constant with constant.

Addition laws

1) The amount does not change from a change in the places of the terms, i.e.
 a+b=b+a

This is the translational law of addition.
2)To add the third term to the sum of two terms, we can add the sum of the second and third terms to the first term, i.e.
 (a+b)+c=a+(b+c)

1)  This is the combined law of addition.
variable coefficient with its similar variable coefficient and constant with constant except that the fact we will include the term additive inverse.

Example:
To subtract  (12a + 7) from  (30a − 2), we have to add the additive inverse of (12a+7) with (30a−2).
Additive inverse of (12a + 7) is −(12a + 7)=(−12a − 7) 
Therefore,
(30a−2)−(12a + 7)=(30a −2) + (−12a −7)=(30a −12a)+(−2 −7)=18a −9

Division of algebraic expressions
    Division is the inverse process of multiplication.
    When we divide one expression by another, we find a third expression which when multiplied by the second gives the first , i.e., if a ÷ b = x then a = bx. In a ÷ b = x, ‘a’ is called the Dividend, ‘b’ the Divisor and ‘x’ is called the Quotient.
    Rules of Signs in Division :
    (i)     When the dividend and the divisor have the same signs, the quotient has the plus sign.
    (ii)     When the dividend and the divisor have opposite signs, the quotient has the negative sign. 

Division of a Monomial by another Monomial :

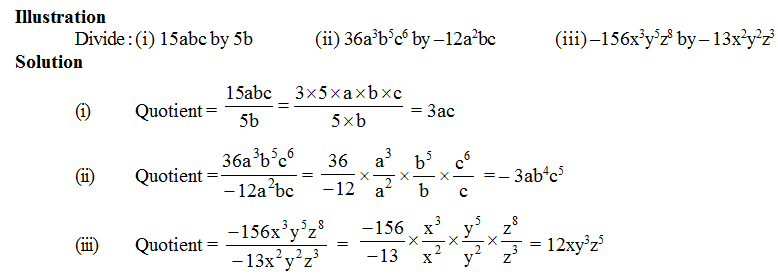
Division of a Polynomial by a Monomial :
       Divide each term of the polynomial by the monomial and then write the resulting quotients.

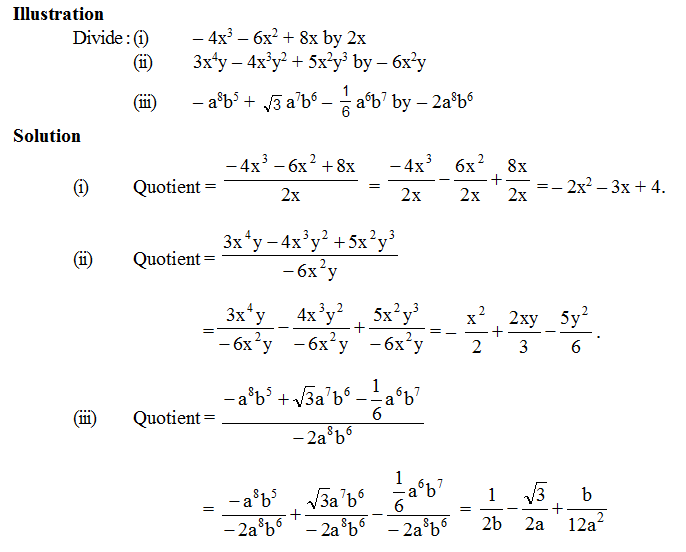
Algebraic identities
    An identity is an equality, which is true for all values of the variables. The following three identities are very important. 

    Identity 1 : (a + b)² = a² + 2ab + b²
    Proof : we have : 
        (a + b)²       = (a + b) (a + b)
              = a (a + b) + b(a + b)
              = a² + ab + ba + b²
              = a² + 2ab + b²                            [Since ba = ab]
   ∴    (a + b)²  = a2 + 2ab + b².  

    Identity 2 : (a – b)² = a² – 2ab + b². 
    Proof : we have 
        (a – b)²     = (a – b) (a – b)
            = a(a – b) – b(a – b) 
            = a² – ab – ba + b² 
            = a² – ab – ab + b²                  [Since ba = ab]
            = a² – 2ab + b².
            = (a² – 2ab + b²) 

Identity 3 : (a + b)(a – b) = a² – b²
    Proof     We have : 
        (a + b) (a – b) = a (a – b) + b(a – b)
                       = a² – ab + ba – b²
                       = a²  – b²                            [Since ba = ab]
   ∴     (a + b)(a–b)    = a² – b².

Applications of the above identities :

    Illustration 
        Find each of the following products : 
         (i) (3x +2y) (3x +2y)             (ii) (4x² + 5) (4x² + 5) 
         (iii) (2x – 5y)²                      (iv) (3x2 +2y²) (3x² – 2y²) 

Solution       
        (i)     (3x +2y)(3x +2y) = (3x +2y)² 
                                           = (3x)² + (2y)² + 2 (3x) (2y)       [Using (a + b)² = a² + b² + 2ab]
                                           = 9x² +4y² + 12xy.     
        ∴     (3x + 2y) (3x + 2y) = 9x² + 4y² + 12xy. 

        (ii)     (4x² + 5)(4x² + 5) = (4x² + 5)² 
                                             = (4x²)² + 5² + 2 (4x²) 5     [Using (a + b)² = a² + b² + 2ab] 

                                            = 16x4 +25 + 40x2. 

        (iiii)     (2x – 5y)² = (2x)² + (5y)² – 2 (2x) (5y)        [Using (a – b)² = a² + b² – 2ab] 
                    = 4x² + 25y² – 20xy. 

        (iv)     (3x² + 2y² )(3x² – 2y²) = (3x²)² – (2y²)²     [∴ (a + b) (a – b) = (a² – b²)] 
                                  = (9x⁴ – 4y⁴).

Multiplication of algebraic expressions
    Following rules of signs and the laws of exponents used in multiplication.

1.     Rules of signs in multiplication : 
    The product of two factors with like signs is positive, and the product of two factors with unlike signs is negative. Thus if a and b are two positive numbers then 

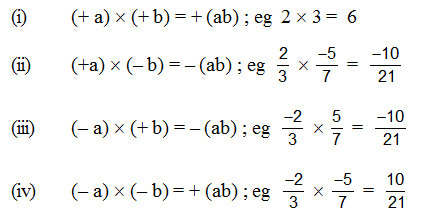
2.    Laws of exponents in multiplication 
       Law of exponents in multiplication is given as :
        a^m x aⁿ  = a^m+n  x e.g. x⁵ x x² = x^{5 + 2} = x⁷ 

Multiplication of a Monomial by a Monomial : 

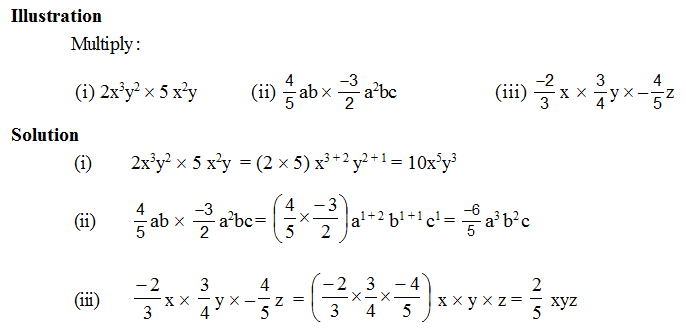
      Thus in multiplication of algebraic expression : 
    (i)     Write the product of the numerical coefficients. 
    (ii)     Write all the different letters occurring in the algebraic expressions giving to each letter an exponent (power) equal to the sum of all the exponents of that letter in the given expressions. 
    (iii)     The sign of the product is minus if there is an odd number of negative factors and plus if there is an even number of negative factors.

Multiplication of a Binomial by a Monomial : 
    In order to multiply a binomial by a monomial use the following rule : 
    a x (b + c)  = a x b + a x c. 

    Illustration 
        Multiply  : (i)   3x² + 4xy by 2x         (ii) –4a [a + 3b]    (iii) – 4a [a – 3b]
    Solution    
        (i)     2x [3x² + 4xy] = 2x x 3x² + 2x x 4xy  = 6x³ + 8x²y 
        (ii)     – 4a [a + 3b]  = – 4a x a  – 4a x 3b = – 4a² – 12ab 
        (iii)     – 4a [a – 3b] = – 4a ´ a – 4a ´ (–3b) = – 4a² + 12 ab. 

Multiplication of a Binomial by a Binomial : 
    In multiplication of a binomial by binomial we will use the law of multiplication of a binomial by a monomial twice. 
    Illustration     
        (i)     (a + b) (c + d) 
        (ii)     (2x² + 3y) (3x² – 2y)
    Solution
         (i)     (a + b) (c + d)     = a (c + d) + b (c + d)
                      = a x c + a x d + b x c + b x d
                     = ac + ad + bc + bd 

        (ii)     (2x² + 3y) (3x² – 2y) 
                    = 2x² (3x² – 2y) + 3y (3x² – 2y)
                    = 2x² x 3x² + 2x² x (– 2y) + 3y x 3x² + 3y x (–2y) 
                    = 6x⁴ – 4x²y + 9x²y – 6y²