1. Proper and Improper fractions
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
INTRODUCTION
In this chapter, we will study :
- What are fractions
- Types of fractions-
(a) Comparison of fractions
(b) Operation on fractions
FRACTIONS
Fraction is a part of whole.

Denominator tells us about into how many equal parts the whole is divided.
Numerator tells us how many parts are considered of the whole
Types of Fractions
1. Decimal fractions : Any fraction whose denominator is in the form of 10n, n ∈ N as i.e.10,100, 1000 etc. is called a decimal fraction.
![]()
2. Vulgar fraction : Any fraction other than decimal fraction is called vulgar fraction.
![]()
3. Proper fraction : Any fraction having its numerator less than its denominator is called a proper fraction.
![]()
4. Improper Fraction : Any fraction whose numerator is greater than or equal to the denominator is called an Improper fraction.
![]()
5. Mixed Fraction : When an improper fraction is expresed as sum of a natural number and a proper fraction is called mixed fraction.
![]()
6. Equivalent Fractions : The fractions obtained by multiplying the numerator and denominator both by the same number are called Equivalent fractions.
![]()
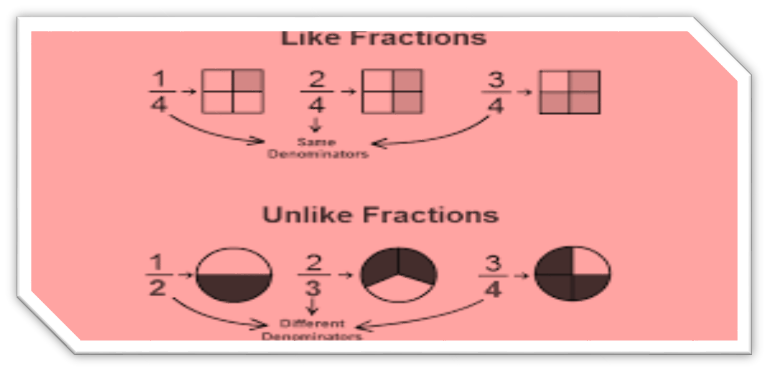
7. Like Fractions : Those fractions which have same denominator but different numerator are called like fractions.
![]()
8. Unlike Fractions : Fractions which do not have common denominator are unlike fractions.
![]()
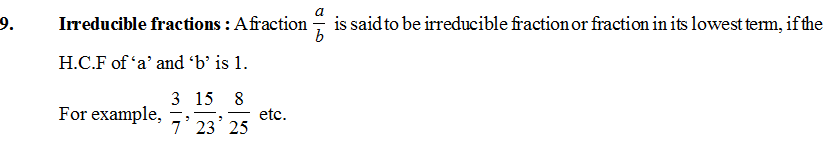
1. Proper and Improper fractions
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
Chapter 2
Fractions and Decimals
Proper and Improper fractions
Types of Fractions
There are three major types of fractions
Proper Fraction
Improper Fraction
Mixed Fraction
Proper Fractions
Proper Fraction
Fractions where numerator is always smaller than the denominator.
It's called proper because the number of region will always be lower than the total number of region. Fore.g.1/3,1/6,2/7,9/10 and so on.

The value of a proper fraction will always be lower than 1.
Improper Fractions
Fractions where numerator is always further than the denominator.

It's called improper because the number of region will be more than the total number of region. Fore.g.5/3,9/6,8/7,
The value of a proper fraction will always be more than 1.
Mixed Fraction
Fractions where there's a combination of a whole and a fractional part. e.g.
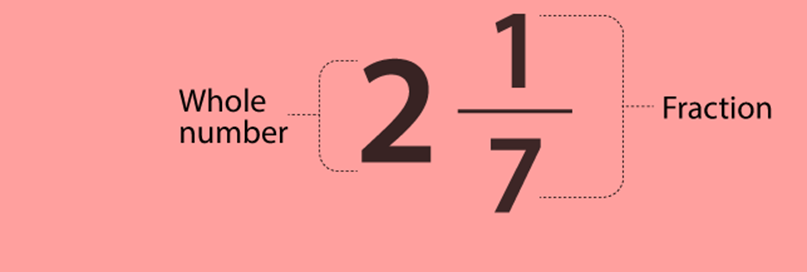
All Improper fractions can be expressed as mixed fractions
Like and Unlike Fractions
Like fractions are fractions with same denominator. For eg ½,15/2,19/2 and so on.
Unlike fractions are fractions with different denominators. Fore.g.16/5,7/8, ½,2/5,2/10.
It's important to note that like and unlike fractions are decided only on the base of denominator. The value of numerator doesn't count.
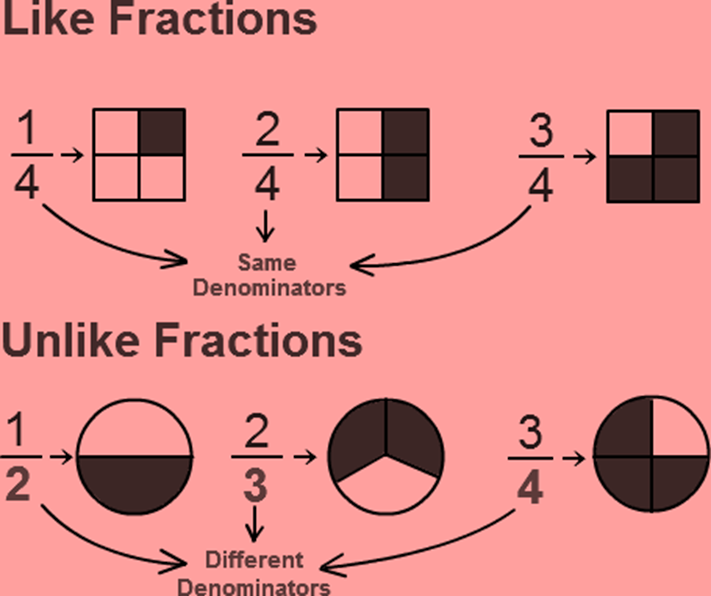
Equivalent Fractions
Equivalent fractions are fractions which represent the same number.
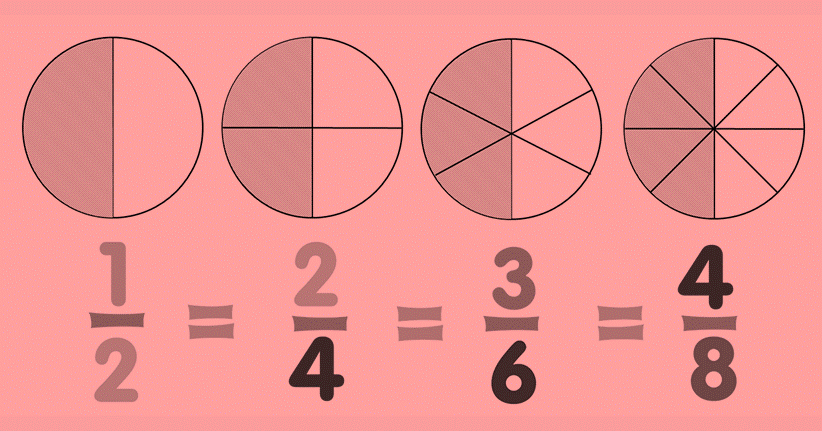
e.g. Dipu divides the pizza into 2 equal halves and eats one half of it. Bholu divides the same pizza into 4 equal halves and eats two region of it.
Pizza Share eaten by Bholu = 2 region out of 4 = 2/4. This can be further reduced to get = ½ = 0.5
Pizza Share eaten by dipu = 1 part of out of 2 = ½.
½ = 0.5.
therefore, although the fractions are2/4 and1/2 but they represent the same numbers. Hence they're equivalent fractions.
In order to make equivalent number, we've to multiply both the numerator and the denominator by the same number. For eg we get the following fractions when we keep on dividing both the numerator and the denominator by the number 2.
These fractions are equivalent since all of them can be reduced to the simplest fraction- ½.
Equivalent fraction can also be formed by separating both the numerator and the denominator by the same number.
It's important to note that the number by which we divide has to be similar that the number divides both the numerator and the denominator ideally.
accordingly, we can first find the HCF of the numerator and the denominator further divide them by the HCF.
These fractions are equivalent since all of them can be reduced to the simplest fraction- ½. Comparing Fractions
Comparing Like Fractions
In like fractions, the denominators are the same. So, only numerators are compared.

The one with bigger numerator is the bigger fractions.
e.g. ¾>1/4
Comparing Unlike Fractions
In unlike fractions, denominators are different.
primarily, we try and make the denominators same.
This is done by converting fractions into equivalent fractions. To do this, the LCM of different denominators.
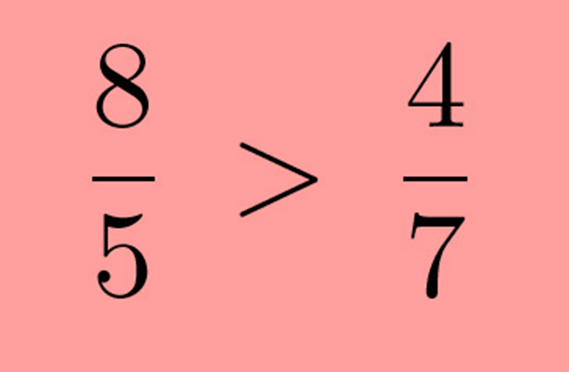
Each fraction is converted into a form like that the LCM as the common denominator of both the fractions.
Comparison of the matching fractions attained can be done by comparing the numerators.
e.g.
LCM of 3 and 4 = 12
Multiply Numerator and denominator of1/3 by 4 similar that the equivalent fraction has 12 in the denominator
1 *4/3 * 4 = 4/12
Multiply Numerator and denominator of2/4 by 3 similar that the equivalent fraction has 12 in the denominator
2 *3/4 * 3 = 6/12
Since the denominators are the same, equating the numerators we get
<6/12
thus,1/3<2/4
Problem Compare the fractions a) 3/ b and5/6 b)1/7 and1/4
result
and5/6 are like fractions because they've common denominators.
5 is greater than 3, so5/6 is more than3/6 and ¼ are unlike fractions.
primarily, we try and form the denominators equal.
This is done by converting fractions into equivalent fractions. To do this, the LCM of different denominators.
The LCM of 7 and 4 is 28. We get
1 *4/7 * 4 and 1 *7/4 * 7
4/28 and7/28
These are like fractions now. Comparing the numerators, we get
<7/28.
2. Operations in Fractions
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Comparison of Fractions
1. Method for comparison of two fractions:
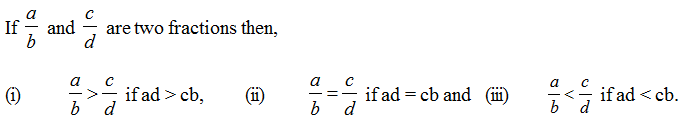
2. Method for comparison of more than 2 fractions:
1st Step : Find the L.C.M. of denominator of all the given fractions.
2nd Step : Convert all the given fractions into like fractions by dividing the L.C.M. with individual denominators and multiplying the result obtained with denominator and numerator, of each fractions.
3rd Step : On comparison of numerator the fraction with smaller numerator is smaller fraction.

Operations on Fractions:
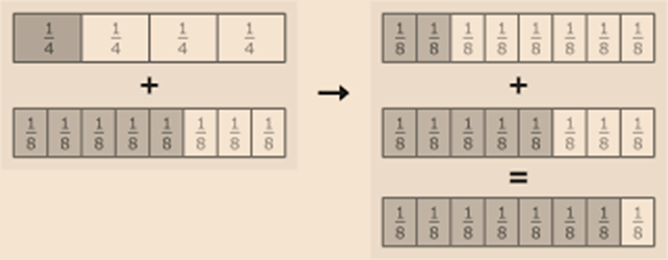
1. Addition of fractions:
Rule 1: In case of like fractions, add the numerators, keeping the denominator same.
![]()
Rule 2: For unlike fractions, addition is done by first converting the fractions into like fractions and then adding. In practice, the addition of unlike fractions is done by using L.C.M.
![]()
Rule 3: Two mixed numbers can be added by adding whole numbers and fractions separately.
![]()
2. Subtraction of Fractions:
Rules for subtraction of fractions is similar to that of addition
(i) Like fractions are subtracted by finding the difference of numerators.
![]()
(ii) Unlike fractions are converted to like fractions and then subtracted.
![]()
2. Operations in Fractions
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
Operations in Fractions
Fundamental operations in fractions:
Addition
Subtraction,
Division,
Multiplication
Addition and subtraction of Fractions
Addition of Like Fractions
Since like fractions have the same denominator, we retain the denominator in the final answer.
We add the numerator to get the numerator of the final fraction.

Subtraction of Like Fractions
Since like fractions have common denominator, we retain the denominator in the denominator.
The numerators are subtracted to get the numerator of the final fraction.
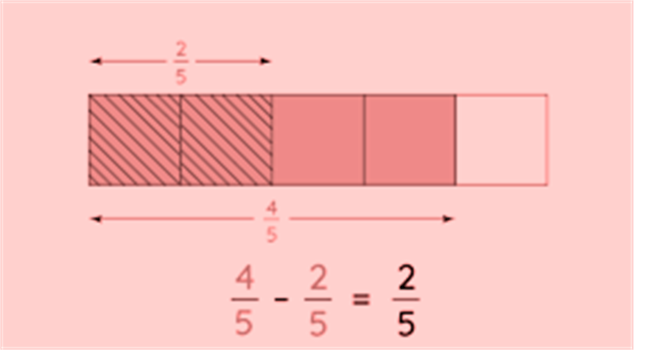
Addition of Unlike Fractions
These fractions have different denominators.
originally, the fractions are converted into equivalent fractions with a common denominator.
To do so, the LCM of denominators is calculated.
The fractions are converted into like fractions with a common denominator.
The common denominator is retained
The numerators are added.
Deduction of Unlike Fractions
These fractions have different denominators.
originally, the fractions are converted into original fractions with a common denominator.
To do so, the LCM of denominators is calculated.
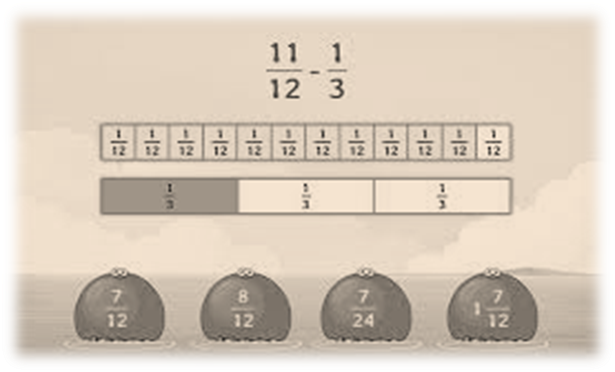
The fractions are converted into like fractions with a common denominator.
The common denominator is retained
The numerators are subtracted.
Multiplication of a Fraction by a Whole Number
To multiply a whole number with a proper or an improper fraction, we multiply the whole number with the numerator of the fraction, keeping the denominator same.
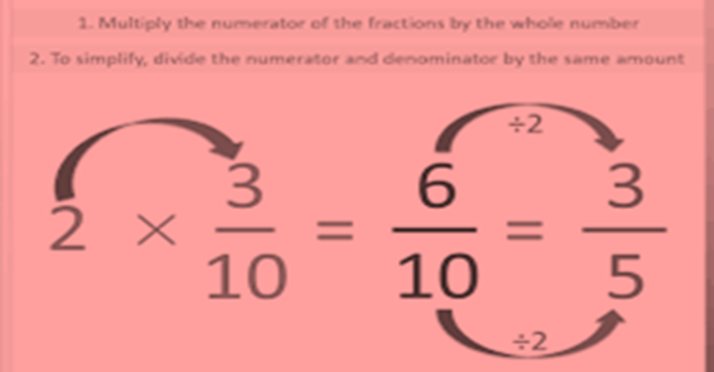
To multiply a mixed fraction to a whole number, first convert the mixed bit to an improper fraction and also multiply.
Multiplication of a Fraction by a fraction
![]()
Still, we first convert into an improper fraction, If one or both of the fractions is a mixed fraction.
When two proper fractions are multiplied, the product is lower than both the fractions. Or, we say the value of the product of two proper fractions is lower than each of the two fractions.
When two improper fractions are multiplied the product of two improper fractions is more than each of the two fragments. Or, the value of the product of two indecorous fragments is further than each of the two fragments.
Division of fractions
Division of a fraction by a whole number
A fraction being divided by a number is original to the bit being multiplied by the supplementary of the number.
A complementary of the number is a number which we multiplied by the original number gives1. Fore.g. the complementary of 2 is ½ since 2 *1/2 = 1. also, the complementary of7/2 is2/7.
In short, a complementary is attained by switching the numerator and denominator.
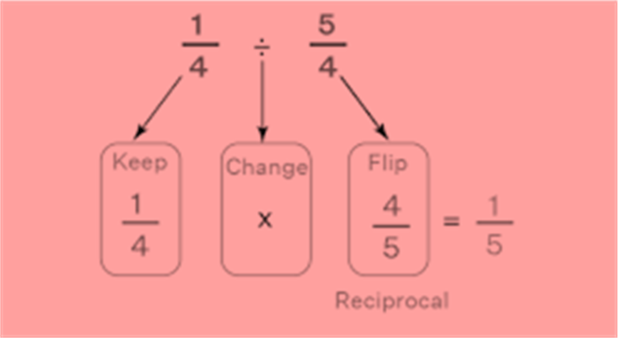
While dividing mixed fractions by whole numbers, convert the mixed fractions into improper fractions
Division of a whole number by a fraction
To divide a whole number by any fraction, multiply that whole number by the complementary of that fraction.
While dividing a whole number by a mixed fraction, first convert the mixed fraction into improper fraction and also answer it.
3. Decimal Numbers
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
3. Multiplication of Fractions :

3. Decimal Numbers
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
Decimal Numbers
Decimals represent fractions
One block divided into 10 equal parts. In fractional terms, each part is 1/10 (one-tenth) of a unit. It can be written as 0.1 in decimal notation.

Comparing Decimals
While comparing two decimal numbers, we consider the following rules:
We compare the place values of digits from left to the right.
Extra zeroes to the right of the last digit of a decimal value do not change the value of the number.
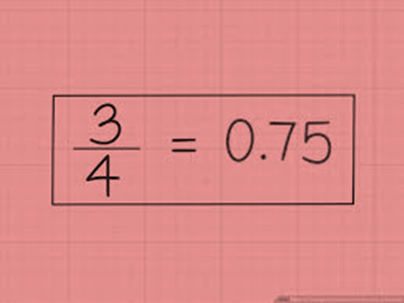
Extra zeroes between decimal point and a decimal digit do not change its value.
4. Basic operations on decimal numbers
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
4. Division of Fractions
Fraction as an operator “of”
To know the fractional part of a quantity fraction and the number (quantity) are multiplied.
![]()
Before understanding the division of fractions, we must know , what is inverse of a fraction.
Inverse of a fraction or reciprocal of fraction: A fraction is said to be inverse of itself, if the places of


4. Basic operations on decimal numbers
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
Basic operations on decimal numbers
Addition and Subtraction of Decimal Numbers
Addition of Decimal numbers:
The rules for addition of numbers with Decimals are:
- Numbers are written under each other. The decimal points lie under each other, in the same vertical line.
- Addition is done column wise.
- Addition is started from the right hand side and then we move to the left hand side.

Subtraction of Decimal numbers:
The rules for subtraction are:
- The smaller number is written under the bigger number.
- The numbers are written in such a way that the decimals are in the same vertical line.
- Subtraction is started from the right hand side.

Multiplication of decimal numbers
When two decimal numbers are multiplied, we simply multiply the numbers (without their decimal points)
Then we count the total number of digits after the decimal point, taking both the decimal numbers.
The decimal point is placed in the product such that the total number of digits after the decimal point is equal to the total number obtained
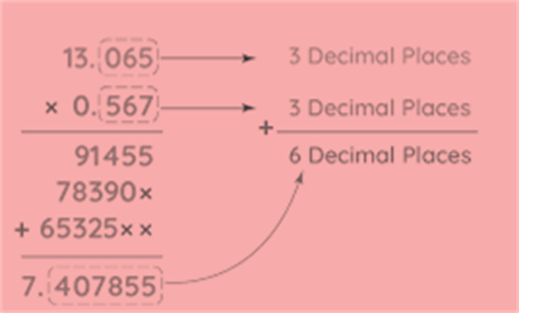
When a decimal number is multiplied by 10, 100 or 1000, the digits in the product are same as in the decimal number but the decimal point in the product is shifted to the right by as , many of places as there are zeros over one.
Division of Decimal Numbers
Firstly, write the decimal numbers in fractional form. For e.g. 0.5 is 5/10.
Multiply the dividend with the reciprocal of divisor. The answer obtained is the required answer.

While dividing a number by 10, 100 or 1000, the digits of the number and the quotient are same but the decimal point in the quotient shifts to the left by as many places as there are zeros over one.
5. Multiplication of decimal numbers
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
DECIMALS
Numbers of the form 12.4, 362.49, 148.3672 etc. are said to be in decimal form.
A decimal number can be expressed into two parts
1. The whole number
2. The decimal part in a decimal number.
The parts are seperated by a point (.) called the decimal point.
In a decimal number the number on left hand side of the decimal is called the whole number part and the number on the right hand side of the point is called the decimal part.
For example, In the number 13.436, 13 is the whole number part and 436 is the decimal part.
Decimal Places - The number of digits in the decimal part give the number of decimal places.
For example, 140.034 has 3 decimal places
Like Decimals - Decimal numbers having same number of decimal places are called like fractions.
For example, 12.32, 143.93, 160.04 etc. are like decimals having two decimals places each.
Unlike Decimals - Decimal numbers having different number of decimal places are called unlike decimals.
For example, 1.362, 3.43, 16.1 etc.
Note: Placing any number of zeroes at the extreme right of the last digit of the decimal place does not change its value. Thus 44.083 = 44.08300 = 44.083000 etc.
Comparison of Decimals numbers
Steps for comparison of decimal numbers :
(i) Convert the decimal number into like decimals by placing zeroes to the right of the decimal.
(ii) Compare the whole number part. The number with greater whole number part is greater.
(iii) If the whole number parts are equal, compare the first digit after decimal. The number with the larger digit in the place right to decimal will be greater.
(iv) If the digit to the right of the decimal is equal then compare the 2nd digit from the right of decimal then the 3rd digit to the right of decimal and so on.
Illustration
Write the following decimal number in ascending order: 6.3, 5.3, 6.03, 4.308, 5.45
Solution
Convert the given fractions into like fraction.
6.300, 5.300, 6.030, 4.308, 5.450 arranging in ascending order after comparison of digits we get,
4.308 < 5.300 < 5.450 < 6.030 < 6.300
Conversion of decimal number into fraction
In order to convert a decimal number into fraction, the digits of the decimal number are kept as numerator without the decimal, and the denominator is kept as 1 followed by the same number of zeroes as there were digits after decimal.
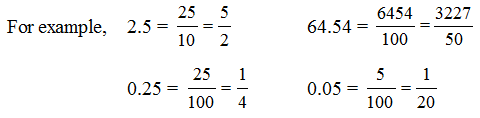
Operation of Decimals
Addition and Subtraction of Decimal Numbers
Steps to add or subtract decimal numbers:
(i) Convert all the decimal number into like decimals
(ii) Add or subtract as required, as per rules of addition or subtraction of whole numbers.
(iii) Place the decimal under decimal point in the given numbers.
Illustration 1
Add : 13.46, 219.54, 2.084
Solution
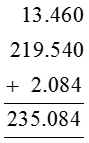
Illustration 2
Subtract : 148.23 – 30.018
Solution
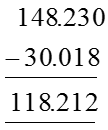
6. Division of decimal numbers
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Multiplication of Decimal Numbers
Multiplication of a decimal numbers by 10 or its factors
Rule: Shift the decimal point to the right place equivalent to numbers of zeros followed by 1.
For example, 5.23 x10 = 52.3
13.438 x 100 = 1343.8 (since in 100 one is followed by 2 zeroes hence the decimal point is shifted to two places to the right)
Multiplication of a decimal by a whole number or by decimal number .
Rule: Multiply the decimal numbers by the whole number or another decimal number as per rules of multiplication.
Rule: Place the decimal in the result at such a place from the left most digit, which is equal to the sum of the places from the left, of the decimal number or whole number and the decimal number which is multiplied.
Illustration 1
Multiply : 0.534 by 2
Solution
The product must contain 3 places of decimal hence 0.534 x 2 = 1.068.
Illustration 2
Multiply : 2.054 x 4.32
Solution
Multiply : 2.054 and 4.32 without putting decimal i.e. 2054 x 432 = 887328
The product must contain 3 + 2 = 5 decimal places. Since sum of the decimal places of the two
numbers = 5 hence 2.054 x 4.32 = 8.87328
Illustration 3
Multiply : 2 × 0.2 × 0.002
Solution
2 × 2 × 2 = 8
Sum of the decimal places of the given numbers = 4 hence the product must contain 4 places of decimals
So 2 × 0.02 × 0.002 = 0.0008
Division of Decimal Numbers
- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Divisions of Decimals
1. Division of a decimal number by factors of 10
Rule: On dividing a decimal number by 10 or its factors, the decimal point is shifted towards left by as many places as are zeroes followed by 1.
For example, 12.75 ÷10 = 1.275 (decimal point is shifted towards left by 1 decimal place as there is 1 zero after 1 in 10.)
For example, 12480.03 ÷ 1000 = 12.48003 (decimal point is shifted towards left by 3 decimal place as there are 3 zeroes followed by 1.
Division of a decimal number by a whole number
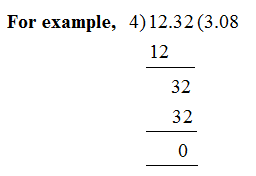
Step - 1: Perform the division by considering the dividend (the decimal number to be divided) as a whole number.
Step - 2: The decimal would be placed in the quoteint once the whole number part of the dividend is complete. Continue the division as in case of whole numbers.
Remark: On dividing the decimal number of a whole number, we can place as many zeroes to the right end of the decimal point of the interval as required to make the remainder zero.
2. Division of a decimal by a decimal:
Step-1: First convert the divisor into a whole number by multiplying the dividend and divisor by suitable factor of 10.
Step-2: Follow the rules of divisions as discussed earlier
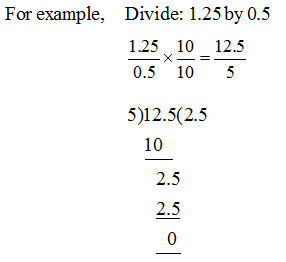
Illustration 1
The cost of 28 toys of the same kind is Rs 3462.20. Find the cost of each toy.
Solution
Cost of 28 toys = Rs 3462.20.
Cost of 1 toy = Rs (3462.20 ÷ 28)
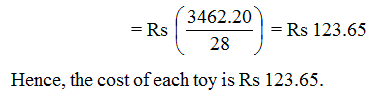
Illustration 2
The product of two decimals is 1.5008 . If one of them is 0.56, find the other.
Solution
Product of given decimals = 1.5008; One decimal = 0.56.
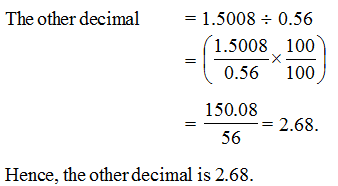

 Param Publication
Param Publication
 ReginaTagebücher
ReginaTagebücher
