1.Zeros of Polynomial
Graphic Interpretation Of The Number Of Zeros Of A Polynomial
A polynomial in variable x is denoted by p(x).
The highest power of the variable in the polynomial is known as its degree. For example, the highest power of variable x in the polynomial x2 − 3x + 2 is 2. Hence, it’s degree is 2.
Let us better understand this concept with a few more examples.
Example1: Find the number of zeroes of the polynomial whose graph is given below.
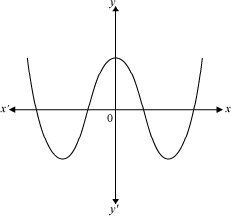
Solution:
The given graph intersects the x- axis at 4 distinct points. Hence, the number of zeroes of the given polynomial is 4.
Example 2: Find the number of zeroes of the polynomial whose graph is given below.

Solution:
The given graph does not intersect the x-axis.
Hence, the given polynomial has no zeroes or in other words, the number of zeroes of the given polynomial is zero.
Example 3: Find the number of zeroes of the polynomials whose graphs are given below.
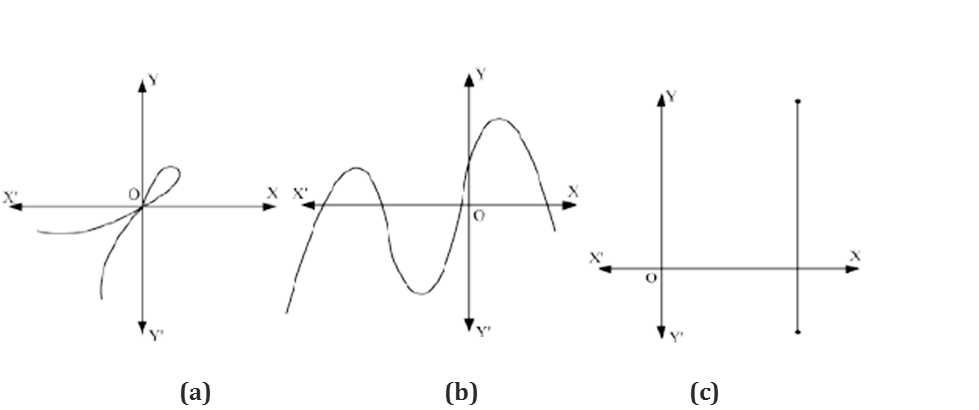
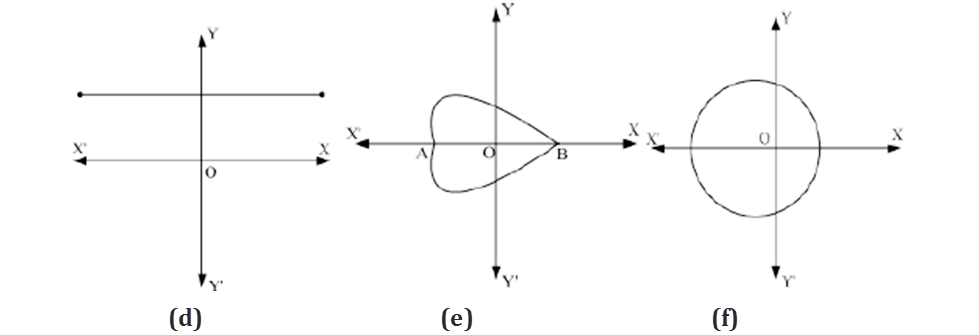
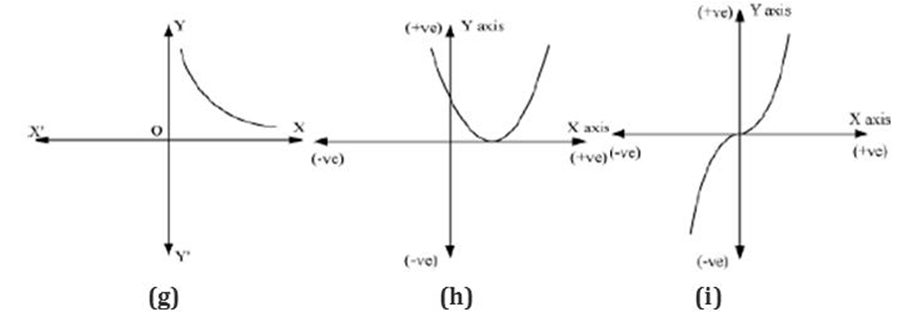

Solution:
(a) The graph intersects the x-axis at only 1 point.
Hence, the number of zeroes of this polynomial is 1.
(b) The graph intersects the x-axis at 4 distinct points.
Hence, the number of zeroes of this polynomial is 4.
(c) The graph intersects the x-axis at only 1 point.
Hence, the number of zeroes of this polynomial is 1.
(d) The graph of the polynomial does not intersect the x-axis.
Hence, this polynomial has no zeroes.
(e) The graph intersects the x-axis at 2 distinct points.
Hence, the number of zeroes of this polynomial is 2.
(f) The graph intersects the x-axis at 2 distinct points.
Hence, the number of zeroes of this polynomial is 2.
(g) The graph of the polynomial does not intersect the x-axis.
Hence, this polynomial has no zeroes.
(h) The graph intersects the x-axis at only 1 point.
Hence, the number of zeroes of this polynomial is 1.
(i) The graph intersects the x-axis at only 1 point.
Hence, the number of zeroes of this polynomial is 1.
(j) The graph intersects the x-axis at 4 distinct points.
Hence, the number of zeroes of this polynomial is 4.
(k) The graph intersects the x-axis at 5 distinct points.
Hence, the number of zeroes of this polynomial is 5.
(l) The graph intersects the x-axis at 3 distinct points.
Hence, the number of zeroes of this polynomial is 3.
Geometrical Interpretation Of Zeros Of Polynomials
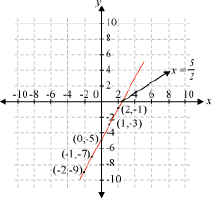
Let us consider a polynomial p(x) = 2x – 5. Its graph can be drawn as follows:
If we notice the above graph carefully, then we can see that the graph of the polynomial p(x) = 2x – 5 passes through the x-axis at a point .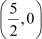
Do you know what is the value of the polynomial p(x) at the x-coordinate of this point? Let us find out how.
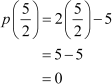
Thus,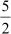 is a zero of the polynomial.
is a zero of the polynomial.
Thus, we can say that

Using the above statement, we can find out the zeroes of the polynomials. The method of finding zeroes can be easily understood with the help of the following example.
Let us find the zeroes of the polynomial p(x) = x2 – 4x + 3. The graph of this polynomial can be drawn as follows:
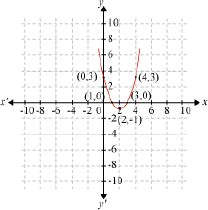
From the graph, we can see that the graph of the polynomial p(x) = x2 – 4x + 3 cuts the x- axis at two points respectively (1, 0) and (3, 0). Now, the x-coordinates of these points are 1 and 3 respectively. Thus, 1 and 3 are the zeroes of the given polynomial p(x) = x2 – 4x + 3.
In this way we can interpret the zeroes of the polynomial geometrically.
Let us discuss one more example based on geometrical interpretation of zeroes of a polynomial.
Example1: Find the zeroes of the polynomials whose graphs are shown below.
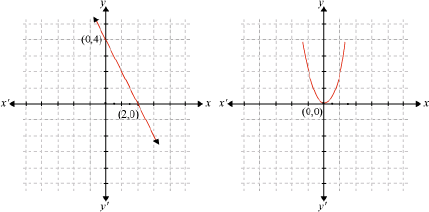

Solution:
(i) The graph of the polynomial intersects the x-axis at the point (2, 0).
The x coordinate of the point (2, 0) is 2.
Thus, 2 is a zero of the polynomial whose graph has been shown.
(ii) The graph of the polynomial intersects the x-axis at the point (0, 0).
The x co-ordinate of the point (0, 0) is 0. Thus, 0 is a zero of the polynomial.
(iii) The graph does not intersect the x-axis, so there is no zero of the polynomial whose graph has been shown.
1.Zeros of Polynomial
- Books Name
- Sample paper Term II Maths
- Publication
- SonikaAnandAcademy
- Course
- CBSE Class 10
- Subject
- Mathmatics
Zeros of polynomial
2x²+3x+5 = 0 find x=-1 is zero of polynomial or not
We put value of x in above equation
2(-1)²+3(-1)+5
2-3+5
4 which is not equal to zero so it is not zero of polynomial
If after calculation its value becomes zero then that was zero of polynomial
1.Zeros of Polynomial
- Books Name
- Mathematics Book for CBSE Class 10
- Publication
- Carrier Point
- Course
- CBSE Class 10
- Subject
- Mathmatics
What is Lorem Ipsum?
Lorem Ipsum is simply dummy text of the printing and typesetting industry. Lorem Ipsum has been the industry's standard dummy text ever since the 1500s, when an unknown printer took a galley of type and scrambled it to make a type specimen book. It has survived not only five centuries, but also the leap into electronic typesetting, remaining essentially unchanged. It was popularised in the 1960s with the release of Letraset sheets containing Lorem Ipsum passages, and more recently with desktop publishing software like Aldus PageMaker including versions of Lorem Ipsum.
1.Zeros of Polynomial
sample
2.Zeros and Coefficients of Polynomial – 1
Relationship Between Zeroes Of A Polynomial And Its Coefficients
We have learnt to find the zeroes or roots of a polynomial. Also, we know that zeroes or roots of a polynomial are those values of its variables for which the polynomial results to zero.
Now, let us learn about the relation between zeroes and the coefficients of the polynomial.
Relationship between the zero and the coefficient of a linear polynomial:
Let p(x) = ax + b be a linear polynomial such that a ≠ 0.
Zero of this polynomial can be obtained by equating it with 0. i.e, p(x) = 0
⇒ ax + b = 0
⇒ ax = –b
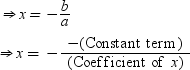
Using this relation, we can find the zero of a linear polynomial.
Relationship between the zeroes and the coefficients of a quadratic polynomial:
Consider a quadratic polynomial p(x) = 3x2– 5x – 12.
Can we find out the sum and the product of the zeroes of this polynomial?
Yes, we can find the sum and the product of zeroes but firstly we have to find out the zeroes of the polynomial.
Here, the zeroes of polynomial p(x) are 3 and .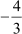
Now, the sum of zeroes = 3 +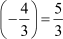
And the product of zeroes = 3 ×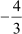 = – 4
= – 4
Can we find out the sum and the product of zeroes by any other method?
Yes, there is also a method in which there is no need to find out the zeroes. In that method we use the coefficients of the polynomial to find the sum and the product of zeroes.
Firstly let us see the relation between the sum and product of zeroes and the coefficients of the polynomial.
Let us first consider a quadratic polynomial p(x) = ax2 + bx + c, where a, b and c are constants.
If αand β are the zeroes of p(x) = ax2 + bx + c, then,

Now, let us find the sum and product of zeroes of the polynomial given in the beginning, using these relations.
The polynomial is p(x) = 3x2 – 5x – 12.
On comparing this equation with ax2 + bx + c, we have
a = 3, b = –5 and c = –12
∴ Sum of zeroes = – 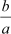 =
=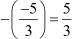
And the product of zeroes =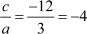
Using these relations we obtained the same values as we found after calculating the zeroes.
Now, let us know the relations between the sum and the product of zeroes and the coefficients of a cubic polynomial.
The general form of a cubic polynomial is p(x) = ax3 + bx2 + cx + d where a, b, c and d are constants.
If α, β and γ are the three zeroes of cubic polynomial p(x), then the relations are given by
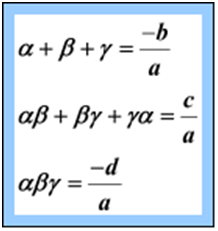
Let us solve some more problems to have a better understanding of the concept.
Example 1: Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(a) x2 – 9x + 20 (b) 5x2 + 21x – 20.
Solution:
(a) The given quadratic polynomial is p(x) = x2 – 9x + 20.
Firstly we will find the zeroes by the method of splitting the middle term and then verify the relationship between the zeroes and the coefficients of the polynomial.
In this method, we have to find two numbers whose product is 20 and sum (or difference) is 9.
Such two numbers are 4 and 5 so, we have
x2 – 9x + 20 = x2 – (4 + 5)x + 20
= x2 – 4x – 5x + 20
= x (x – 4) – 5 (x – 4)
= (x – 4) (x – 5)
Thus, for finding zeroes, we put
x2 – 9x + 20 = 0.
(x – 4) (x – 5) = 0
(x – 4) = 0 or (x – 5) = 0
x = 4 or 5
Thus, 4 and 5 are the zeroes of the polynomial p(x) = x2 – 9x + 20.
Now sum of zeroes = 4 + 5 = 9
And product of zeroes = 4 × 5 = 20
Now, on comparing p(x) = x2 – 9x + 20 with the general quadratic polynomial
ax2 + bx + c = 0, we have a = 1, b = –9 and c = 20.
Using the formulae, we have
Sum of zeroes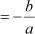
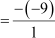
= 9
Product of zeroes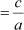
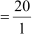
= 20
Hence, it is verified that Sum of zeroes = 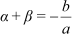 and
and
Product of zeroes = αβ = .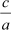
(b) Comparing the given polynomial with ax2 + bx + c, we have, a = 5, b = 21
and c = – 20.
Using the method of splitting the middle term we have,
p(x) = 5x2 + 21 x – 20 = 5x2 + (25 – 4)x – 20
= 5x2 + 25x –4 x – 20
= 5x(x + 5) –4 (x + 5)
= (x + 5) (5x – 4)
For finding zeroes, put p(x) = 0 (x + 5) (5x – 4) = 0
x = – 5 or x =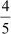
Thus, the zeroes of the polynomial 5x2 + 21 x – 20 are – 5 and 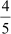 .
.
Now, sum of zeroes = – 5 + 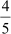 =
=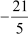 =
=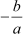
And product of zeroes = – 5 ×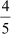 = –4 =
= –4 = 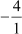 =
= 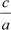
Hence, verified.
Example 2: If 1, 2, and 6 are the zeroes of the cubic polynomial x3 – 9x2 + 20x – 12, then verify the relations between the zeroes and the coefficients.
Solution:
The given cubic polynomial is p(x) = x3 – 9x2 + 20x – 12.
On comparing the given polynomial with the general form ax3 + bx2 + cx + d of cubic polynomial, we have a = 1, b = – 9, c = 20, d = – 12.
Now the zeroes are 1, 2, and 6.
Let α = 1, β = 2 and γ = 6
Now α+ β + γ = 1 + 2 + 6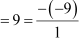
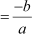
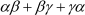 = 1 × 2 + 2 × 6 + 6 × 1
= 1 × 2 + 2 × 6 + 6 × 1
= 2 + 12 + 6
= 20
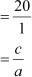
and αβ γ = 1 × 2 × 6
= 12
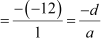
Hence, this verifies the relations between the coefficients and the zeroes of the cubic polynomial.
Formation Of Polynomial Using The Sum And Product Of Zeroes
5 and –3 are the zeroes of a quadratic polynomial p(x). Can we form the quadratic polynomial with the help of these zeroes?
Yes, we can. Let us see how we can form the polynomial.
5 is a zero of the polynomial, it means that (x – 5) is a factor of the polynomial p(x). Similarly (x + 3) is also a factor of the polynomial p(x). We know that a quadratic polynomial can have only two linear factors. Thus, we can write the polynomial p(x) as follows:
p(x) = (x – 5) (x + 3)
= x2 + (– 5 + 3) x + (– 5) (3)
[Using the identity (x + a) (x + b) = x2 + (a + b) x + ab, where a = – 5 and b = 3]
Thus, p(x) = x2 – 2x – 15
This is the required quadratic polynomial.
If we know the zeroes of the quadratic polynomial, then we can find the polynomial as above. On the other hand, if we know the sum and product of the zeroes of the polynomial, then we can use the following formula to find the polynomial.

For example: if the sum and the product of the zeroes of a polynomial are 2 and –8 respectively, then find the polynomial.
Using the above formula, we have
p(x) = x2 – (2)x + (–8)
p(x) = x2 – 2x – 8
In this way, we can find the polynomial if the relationship between the zeroes is known to us.
Let us discuss some more examples based on formation of quadratic polynomial using sum and products of zeroes.
Example 1: If the sum and product of zeroes of a quadratic polynomial are 13 and 36 respectively, find the quadratic polynomial.
Solution:
Let the polynomial be p(x).
It is given that the sum of the zeroes of the polynomial = 13 and the product of the zeroes of the polynomial = 36
But we know that the quadratic polynomial p(x) in terms of sum and product of zeroes is given by the formula
p(x) = x2 – (sum of zeroes)x + product of zeroes
so, we have
p(x) = x2 – 13x + 36
Therefore, x2 – 13x + 36 is the quadratic polynomial whose sum and the product of zeroes are 13 and 36 respectively.
Example 2: If the sum and product of zeroes of a quadratic polynomial are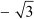 and – 6 respectively, find the quadratic polynomial.
and – 6 respectively, find the quadratic polynomial.
Solution:
Let the quadratic polynomial be p(x).
It is given that the sum of the zeroes of the polynomial is 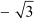 and the product of the zeroes of the polynomial is – 6.
and the product of the zeroes of the polynomial is – 6.
We know that the quadratic polynomial p(x) in terms of sum and product of zeroes is given by the formula
p(x) = x2 – (sum of zeroes)x + product of zeroes so, we have
p(x) = x2 – ( 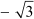 )x + (– 6)
)x + (– 6)
p(x) = x2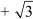 x – 6
x – 6
Therefore, x2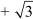 x – 6 is the quadratic polynomial whose sum and product of zeroes are
x – 6 is the quadratic polynomial whose sum and product of zeroes are 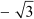 and – 6 respectively.
and – 6 respectively.
Example 3: If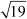 and
and 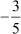 are the zeroes of a quadratic polynomial, then find the polynomial.
are the zeroes of a quadratic polynomial, then find the polynomial.
Solution:
Let p(x) be the required quadratic polynomial. 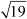 and
and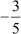 are the zeroes of the polynomial p(x).
are the zeroes of the polynomial p(x).
Now, the sum of zeroes =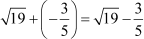
and the product of zeroes =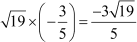
Now, the polynomial is given by the formula
p(x) = x2 – (sum of zeroes)x + product of zeroes
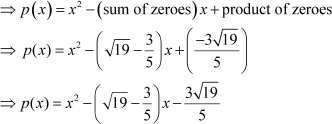
Hence, this is the required polynomial whose zeroes are 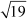 and
and 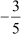 respectively.
respectively.
3.Zeros and Coefficients of Polynomial – 2
Division Of Polynomials by Polynomials (Degree More than 1) Using Long Division Method
All of us have already studied the method of long division of polynomials by other polynomials in earlier classes. But there, our divisor was just of degree one. Now we will
revise long division method of polynomials with other polynomials and extend the discussion to do the division when the divisor is of a higher degree.
Let us discuss the method of division by taking an example. Let us divide (x3 − 7x + 6) by (x2 + 2x − 3).
Now let us solve some examples to practice the above method.
Example 1: Divide the polynomial by monomial and write the quotient and remainder.
(i) 36n5 – 3n3 + 12n2 ÷ 9n2
(ii) 7p7 + 3p5 – 42p3 + 10 ÷ 21p3
Solution:
(i) 36n5 – 3n3 + 12n2 can be divided by 9n2 using long division method as follows:
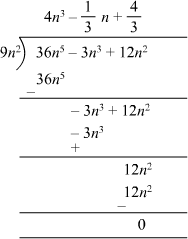
Therefore,
Quotient = 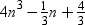
Remainder = 0
(ii) 7p7 + 3p5 – 42p3 + 10 can be divided by 21p3 using long division method as follows:
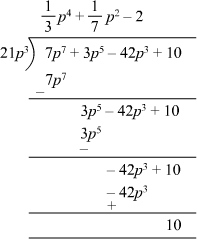
Therefore,
Quotient = 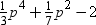
Remainder = 10
Example 2: Check whether (x2 − 3x + 2) is a factor of (x3 − 7x2 + 14x − 8) or not. Solution:
(x2 − 3x + 2) will be a factor of (x3 − 7x2 + 14x − 8), if the polynomial (x3 − 7x2 + 14x − 8) on dividing by (x2 − 3x + 2) gives remainder zero.
The division has been shown below:
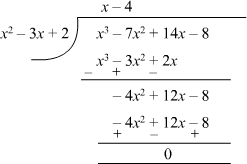
The remainder is zero.
∴ (x2 − 3x + 2) is a factor of (x3 − 7x2 + 14x − 8).
Example 3: Find the quotient and remainder when (15x − 4 + x3 − 6x2) is divided by
(x2 − 3x + 2).
Solution:
Firstly, we arrange the terms of the dividend and the divisor in the standard form.
The dividend in the standard form will be
x3 − 6x2 + 15x − 4.
The divisor is already in standard form. The division has been shown below:
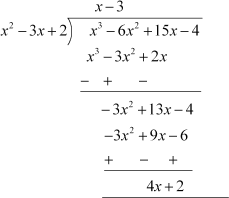
Therefore, Quotient = x – 3
Remainder = 4x + 2
Example 4: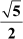 and
and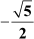 are the zeroes of the polynomial 16x4 − 64x3 + 40x2 + 80x − 75. Find the other zeroes of the polynomial.
are the zeroes of the polynomial 16x4 − 64x3 + 40x2 + 80x − 75. Find the other zeroes of the polynomial.
Solution:
Let p(x) = 16 x4 − 64x3 + 40x2 + 80x − 75
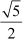 and
and 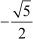 are two zeroes of p(x).
are two zeroes of p(x).
⇒ (x −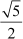 ) and (x +
) and (x +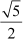 ) are the factors of p(x)
) are the factors of p(x)
⇒ x2 −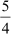 is a factor of p(x)
is a factor of p(x)
To find the other factors, we have to divide p(x) by x2 − 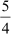 as follows:
as follows:
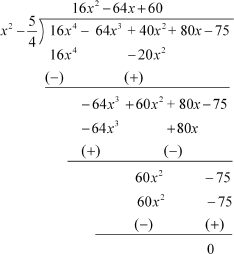
Now, 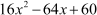 is the factor of p(x).
is the factor of p(x).
So, we can write 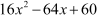 =
=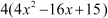
=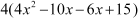 (Splitting the middle term)
(Splitting the middle term)
=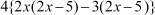
=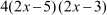
To find the zeroes, put 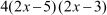 = 0
= 0
We have 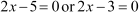
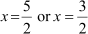
Thus, the remaining zeroes of the polynomial are x =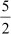 and
and 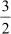 .
.
4.Division of Polynomial
Division Algorithm Of Polynomials
We are aware of the process of division of numbers. Let us divide 487 by 3. We can divide 487 by 3 as follows:
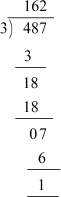
From the above division, we can see that when we divide 487 by 3, we get 1 as remainder and 162 as quotient.
We can also write the dividend 487 in terms of divisor, quotient and remainder as follows: 487 = 3 × 162 + 1
Thus, for real numbers we can write
Dividend = Divisor × Quotient + Remainder
In the same way, we can also divide a polynomial p(x) by another polynomial g(x) when the degree of the polynomial p(x) is greater than or equal to the degree of polynomial g(x). The above relation is also true in case of polynomials and then it is known as division algorithm of polynomials.
Using the division algorithm of polynomials, we can also find any one of the values among p(x), g(x), q(x) and r(x) if other three are known.
Note that degree of q(x) = degree of p(x) – degree of g(x)
Let us discuss more examples based on division algorithm of polynomials.
Example 1: Find the quotient, if the polynomial −2x3 + 7x2 − 7x − 2 when divided by 2x2 − 5x + 2 gives remainder −4.
Solution:
Let the quotient be q(x).
It is given that when we divide the polynomial (−2x3 + 7x2 − 7x − 2) by (2x2 − 5x + 2), we get the q(x) as quotient and −4 as remainder.
Thus, we have
p(x) = −2x3 + 7x2 − 7x − 2
g(x) = 2x2 − 5x + 2
r(x) = −4
We know that the division algorithm for polynomials is:
p(x) = g(x) × q(x) + r(x)
Now, on putting the values in this equation, we have
−2x3 + 7x2 − 7x − 2 = (2x2 − 5x + 2) × q(x) − 4
⇒ −2x3 + 7x2 − 7x − 2 + 4 = (2x2 − 5x + 2) × q(x)
⇒ −2x3 + 7x2 − 7x + 2 = (2x2 − 5x + 2) × q(x)
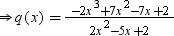
We can divide −2x3 + 7x2 − 7x + 2 by (2x2 − 5x + 2) as follows:
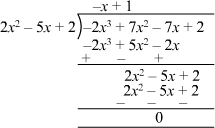
Now, we have q(x) = 1 − x
Therefore, the quotient is 1 − x.
Example 2: Find the quotient, if the polynomial 3x3 − 3x2 + 9x + 2 when divided by x2 + 5x + 1 gives remainder 4x3.
Solution:
Let the quotient be q(x).
It is given that when we divide the polynomial (3x3 − 3x2 + 9x + 2) by (x2 + 5x + 1), we get the q(x) as quotient and 4x3 as remainder.
Thus, we have
p(x) = 3x3 − 3x2 + 9x + 2
g(x) = x2 + 5x + 1
r(x) = 4x3
We know that the division algorithm for polynomials is:
p(x) = g(x) × q(x) + r(x)
Now, on putting the values in this equation, we have
3x3 − 3x2 + 9x + 2 = (x2 + 5x + 1) × q(x) + 4x3
⇒ 3x3 − 3x2 + 9x + 2 − 4x3 = (x2 + 5x + 1) × q(x)
⇒ −x3 − 3x2 + 9x + 2 = (x2 + 5x + 1) × q(x)
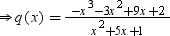
We can divide −x3 − 3x2 + 9x + 2 by (x2 + 5x + 1) as follows:
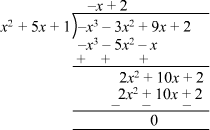
Now, we have q(x) = 2 − x
Therefore, the quotient is 2 − x.
Example 3: By applying division algorithm, find the quotient and remainder when p(x)
= x4 + 3x3 + 2x2 + 5x – 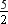 is divided by g(x) = x3 + 2x – 1.
is divided by g(x) = x3 + 2x – 1.
Solution:
p(x) = x4 + 3x3 + 2x2 + 5x – 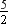 , g(x) = x3 + 2x – 1
, g(x) = x3 + 2x – 1
deg p(x) = 4, deg g(x) = 3
Degree of quotient q(x) = 4 – 3 = 1, and deg of remainder r(x) < deg g(x) = 3 Let q(x) = ax + b, r(x) = cx2 + dx + e
By division algorithm,
p(x) = g(x) × q(x) + r(x)
⇒ x4 + 3x3 + 2x2 + 5x – 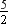 = (ax + b)(x3 + 2x – 1) + (cx2 + dx + e)
= (ax + b)(x3 + 2x – 1) + (cx2 + dx + e)
= ax4 + 2ax2 – ax + bx3 + 2bx – b + cx2 + dx + e
= ax4 + bx3 + (2a + c)x2 + (–a + 2b + d)x + (–b + e)
Equating the coefficients of respective powers, we obtain
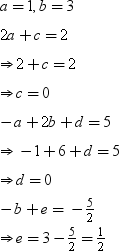
Quotient, q (x) = x + 3
Remainder, r (x) = 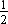

 ACERISE INDIA
ACERISE INDIA
 SonikaAnandAcademy
SonikaAnandAcademy
