1.Similar Figures

Difference Between Similarity and Congruence

Similar figures and congruent figures may appear to be closely related concepts, but there is an important difference between them.

Congruency of line segments:

“Two line segments are congruent to each other if their lengths are equal”.

Consider the following line segments.

Here, the line segments AB and PQ will be congruent to each other, if they are of equal length.

Conversely, we can say that, “Two line segments are of equal length if they are congruent to each other”.

i.e. if 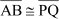, then AB = PQ.

Congruency of angles:

“Two angles are said to be congruent to each other if they have the same measure”.

The angles shown in the following figures are congruent to each other as both the angles are of the same measure 45°.

Thus, we can write ∠BAC ≅ ∠QPR.

Its converse is also true.

“If two angles are congruent to each other, then their measures are also equal”.

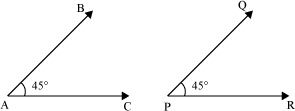
There is one special thing about congruent figures that their corresponding parts are always equal.

For example, if two triangles are congruent then their corresponding sides will be equal. Also, their corresponding angles will be equal.

Look at the following triangles.

Here, ∆ABC ∆DEF under the correspondence ∆ABC ↔ ∆DEF. This correspondence rule represents that in given triangles, AB ↔ DE (AB corresponds to DE), BC ↔ EF, CA ↔ FD, ∠A

— ∠D, ∠B ↔ ∠E, ∠C ↔ ∠F. These are corresponding parts of congruent triangles (CPCT), ∆ABC and∆DEF.

Since ∆ABC and ∆DEF are congruent, their corresponding parts are equal. Therefore, AB = DE, BC = EF, CA = FD

And, ∠A = ∠D, ∠B = ∠E, ∠C = ∠F

Similarly, we can apply the method of CPCT on other congruent triangles also. Let us now try and apply what we have just learnt in some examples.

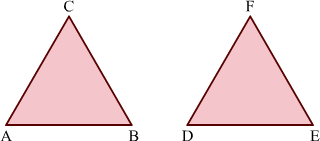
Example 1: Find which of the pairs of line segments are congruent.

(i)

(ii)

Solution:

(i)    Lengths of the two line segments are not same. Therefore, they are not congruent.

(ii)    Each of the line segments is of length 3.1 cm, i.e. they are equal. Therefore, they are congruent.
 

Example 2: If 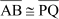and 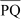= 9 cm, then find the length of 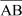. Solution:

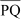Since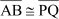 , i.e. line segment AB is congruent to line segment PQ,

therefore, and are of equal length.

∴ = 9 cm

Example 3: If ∠ABC ∠PQR and ∠PQR = 75o, then find the measure of ∠ABC. Solution:

If two angles are congruent, then their measures are equal.

Since ∠ABC ≅ ∠PQR,

∴ ∠ABC = ∠PQR T

herefore, ∠ABC = 75^o

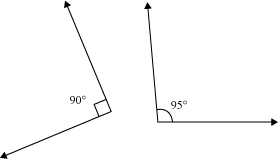
Example 4: Which of the following pairs of angles are congruent?

(i)

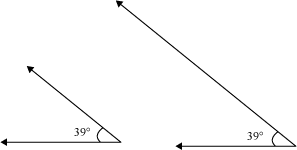
(ii)

Solution:

(i)    The measure of both the angles is the same. Therefore, they are congruent.

(ii)    The measures of the two angles are different. Therefore, they are not congruent.

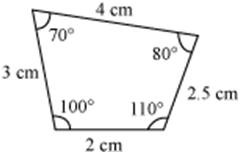
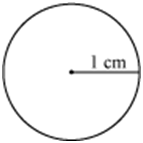
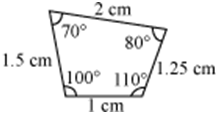
Example 5: Identify the pairs of similar and congruent figures from the following. 

(i)

(ii)

(iii)    

(iv)    

(v)    

(vi)    

(vii)    

(viii)    

Solution:

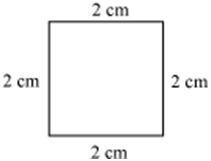
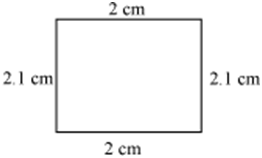
Figures (i) and (iii) are similar because their corresponding angles are equal and their corresponding sides are in the same ratio. However, these figures are not congruent as they are of different sizes.

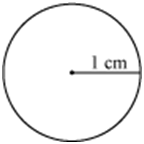
Figures (ii) and (viii) are congruent as they are of the same shape and size (circles with radius 1 cm each).

Example 6:

Are the following figures similar or congruent?

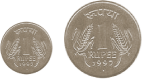
Solution:

The two given figures show two one-rupee coins. As both the figures represent the same coin in two different sizes, they are similar to each other. However, the pictures are not congruent because of their different sizes.

Example 7: In the following figure, ΔPQR and ΔSTU are congruent.

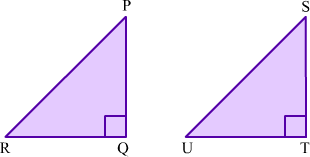
If PQ = 8 cm, QR = 6 cm then find the perimeter of ΔSTU.

Solution:

In ΔPQR, we have

PQ = 8 cm, QR = 6 cm and ∠Q = 90°

Applying Pythagoras theorem in ΔPQR, we obtain

RP² = PQ² + QR²

⇒ RP² = 8² + 6²

⇒ RP² = 64 + 36

⇒ RP² = 100

⇒ RP = 10 cm

Since ΔPQR and ΔSTU are congruent, their corresponding parts will be equal. Therefore,

PQ = 8 cm = ST (CPCT)

QR = 6 cm = TU and (CPCT) RP = 10 cm = US (CPCT)

∴ Perimeter of ΔSTU = ST + TU + US = 8 cm + 6 cm + 10 cm = 24 cm

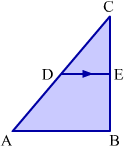
Basic Proportionality Theorem and Its Converse

Consider the following figure.

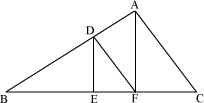
In the above figure, DE is parallel to AF and DF is parallel to AC. Can we say that point E divides BF in the same ratio in which point F divides BC?

For this, we have to prove that .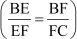

To prove it, we should have the knowledge of basic proportionality theorem (Thales theorem).

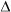Now, let us solve the problem discussed in the beginning with the help of BPT. In ABF, we know that AF is parallel to DE.

Thus, using BPT,

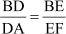… (1)

Similarly in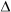 ABC, DF is parallel to AC. Thus, using BPT,

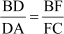… (2)

From equations (1) and (2), we obtain

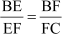
Thus, we can say that point E divides BF in the same ratio in which point F divides BC. The converse of BPT is also true, which can be stated as follows.

“If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side”.

Corollary of BPT:

If a line is drawn parallel to a side of a triangle, then the sides of the new triangle formed are proportional to the sides of the given triangle.

I.e, In the given figure, if DE || AB, then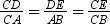

Applications of Basic Proportionality Theorem:

There are two very important properties based on BPT which are as follows:

1. Property of intercepts made by three parallel lines on a transversal.
2. Property of angle bisector of a triangle.

Let us discuss these properties in detail along with their proofs.

Property 1: Intercept Theorem

The lengths of the intercepts made by three parallel lines on one transversal are in the same ratio as the lengths of the corresponding intercepts made by the same lines on any other transversal.

Let us prove this property.

Given: line l || line m || line n

Transversal x intersects these lines at points P, Q and R while transversal y intersects these lines at points S, T and U.

To prove: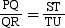

Construction: Draw a line segment PU intersecting line m at point M.

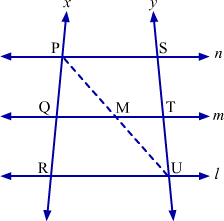
Proof:

In ΔPRU, we have QM || RU

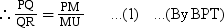
Similarly, in ΔUSP, we have TM || SP

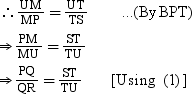
Hence proved.

Property 2: Angle Bisector Theorem

In a triangle, the angle bisector divides the side opposite to the angle in the ratio same as the ratio of remaining sides.

Let us prove this property.

Given: In ΔPQR, ray RT bisects ∠PRQ.

To prove: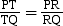

Construction: Draw a ray from Q parallel to ray RT such that it intersects extended PR at S.

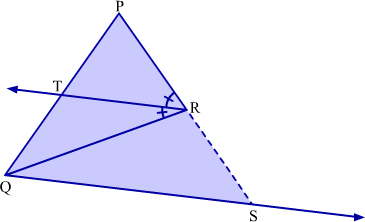
Proof:

We have,

RT || QS and PS is transversal

∴ ∠PRT = ∠RSQ ...(1) (Corresponding angles)

Considering other transversal RQ, we obtain

∠TRQ = ∠RQS ...(2) (Alternate angles) But ∠PRT = ∠TRQ (RT bisects ∠PRQ)

∴ ∠RSQ = ∠RQS [Using (1) and (2)]

Thus, in ΔRQS,

RS = RQ ...(3) (Side opposite to equal angles are equal) Now, in ΔPQS, we have

RT || QS

Hence proved.

Property 3: Converse of Angle Bisector Theorem

If a straight line through one vertex of a triangle divides the opposite side in the ratio of the other two sides, then the line bisects the angle at the vertex.

Let us prove this property.

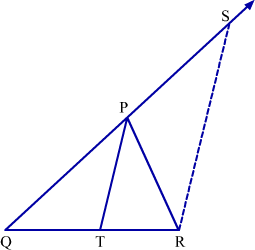
Given: In ΔPQR, line PT divides the opposite side BC internally such that.

Hence proved.

These properties are very useful sometimes.

Let us now solve some examples based on BPT, its converse and properties related to BPT.

Example 1: In triangle ABC, D and E are points on the sides AB and AC, such that AB =11.2 cm, AD = 2.8 cm, AC = 14.4 cm, and AE = 3.6 cm. Show that DE is parallel to BC.

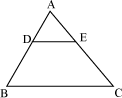
Solution:

It is given that,

AB = 11.2 cm, AD = 2.8 cm, AC =14.4 cm, and AE = 3.6 cm

Therefore, BD = AB – AD = 11.2 – 2.8 = 8.4 cm

And,

EC = AC –AE =14.4 – 3.6 = 10.8 cm

Now,

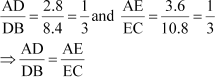
Thus, DE divides sides AB and AC of triangle ABC in the same ratio. Therefore, by the converse of BPT, we obtain that DE is parallel to BC.

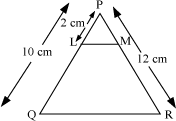
Example 2: In the figure shown below, find the length of PM, if it is given that LM || QR. The corresponding measures are shown in the figure.

Solution:

Here, LM || QR

Then, using basic proportionality theorem, we obtain

Let PM = x cm

Then, MR = 12 – x cm And, PL = 2 cm

LQ = 10 cm – 2 cm = 8 cm

On putting these values in equation (i), we obtain

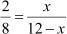
2(12 – x) = 8x

24 – 2x = 8x

24 = 8x + 2x

24 = 10x

x = 2.4 cm

Thus, PM = 2.4 cm

Example 3: If ABCD is a trapezium with AD || BC, then prove that , where O is the point of intersection of diagonals AC and BD.

Solution:

A trapezium has been shown in the following figure.

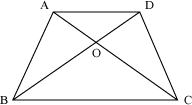
A line LM is drawn parallel to AD and BC and passing through O.

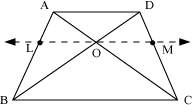
Here, LO || BC.

Using BPT in ΔABC,

Similarly, using BPT in ΔABD as LO || AD, we obtain

From equations (i) and (ii), we obtain

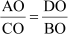
Hence, proved

Example 4: In ΔPQR, LM || QR and L is the mid-point of side PQ. Show that PM = MR.

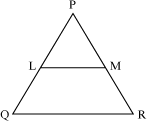
Solution:

Here, LM || QR

Using basic proportionality theorem (BPT),

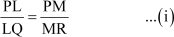
Now, L is the mid-point of PQ.

∴ PL = LQ

Using this in equation (i), we obtain

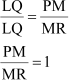
∴ PM = MR

Hence, proved

Example 5: In trapezium ABCD, AB || EF || DC. Find the length of BF and FC.

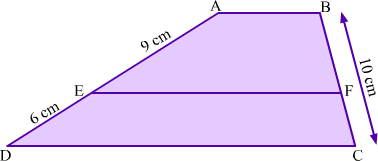
Solution:

In trapezium ABCD, AB || EF || DC.

Here, AD and BC are transversals to parallel segments AB, EF and DC.

Intercepts made by AD are AE and ED while intercepts made by BC are BF and FC. Using property of intercepts made by three parallel lines on a transversal, we obtain

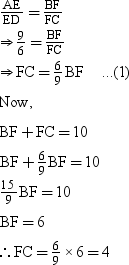
Thus, BF = 6 cm and FC = 4 cm.

Example 6: In ΔABC, BD bisects ∠ABC. Find the length of AD.

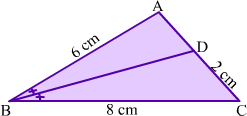
Solution:

In ΔABC, BD bisects ∠ABC

Thus, by using the property of angle bisector of a triangle, we obtain

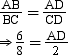
⇒ AD = 1.5

Hence, the length of AD is 1.5 cm.

Example 7.

In the given figure, DE || AB. If perimeter of Δ ABC : perimeter of ΔCDE = 4:5 and DE = 1.2 cm, then find the length of AB.

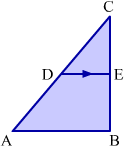
Answer:

It is given that, perimeter of ΔABC : perimeter of ΔCDE = 4:5 and DE = 1.2. InΔ ABC, DE || AB.

By applying the corollary of basic proportionality theorem, we get