Division Of Polynomials by Polynomials (Degree More than 1) Using Long Division Method
All of us have already studied the method of long division of polynomials by other polynomials in earlier classes. But there, our divisor was just of degree one. Now we will
revise long division method of polynomials with other polynomials and extend the discussion to do the division when the divisor is of a higher degree.
Let us discuss the method of division by taking an example. Let us divide (x3 − 7x + 6) by (x2 + 2x − 3).
Now let us solve some examples to practice the above method.
Example 1: Divide the polynomial by monomial and write the quotient and remainder.
(i) 36n5 – 3n3 + 12n2 ÷ 9n2
(ii) 7p7 + 3p5 – 42p3 + 10 ÷ 21p3
Solution:
(i) 36n5 – 3n3 + 12n2 can be divided by 9n2 using long division method as follows:
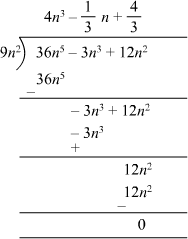
Therefore,
Quotient = 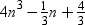
Remainder = 0
(ii) 7p7 + 3p5 – 42p3 + 10 can be divided by 21p3 using long division method as follows:
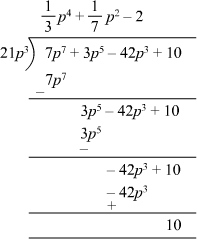
Therefore,
Quotient = 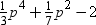
Remainder = 10
Example 2: Check whether (x2 − 3x + 2) is a factor of (x3 − 7x2 + 14x − 8) or not. Solution:
(x2 − 3x + 2) will be a factor of (x3 − 7x2 + 14x − 8), if the polynomial (x3 − 7x2 + 14x − 8) on dividing by (x2 − 3x + 2) gives remainder zero.
The division has been shown below:
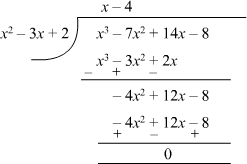
The remainder is zero.
∴ (x2 − 3x + 2) is a factor of (x3 − 7x2 + 14x − 8).
Example 3: Find the quotient and remainder when (15x − 4 + x3 − 6x2) is divided by
(x2 − 3x + 2).
Solution:
Firstly, we arrange the terms of the dividend and the divisor in the standard form.
The dividend in the standard form will be
x3 − 6x2 + 15x − 4.
The divisor is already in standard form. The division has been shown below:
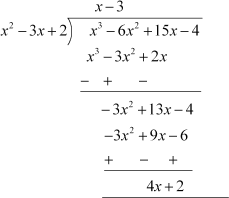
Therefore, Quotient = x – 3
Remainder = 4x + 2
Example 4: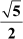 and
and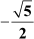 are the zeroes of the polynomial 16x4 − 64x3 + 40x2 + 80x − 75. Find the other zeroes of the polynomial.
are the zeroes of the polynomial 16x4 − 64x3 + 40x2 + 80x − 75. Find the other zeroes of the polynomial.
Solution:
Let p(x) = 16 x4 − 64x3 + 40x2 + 80x − 75
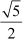 and
and 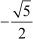 are two zeroes of p(x).
are two zeroes of p(x).
⇒ (x −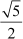 ) and (x +
) and (x +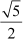 ) are the factors of p(x)
) are the factors of p(x)
⇒ x2 −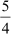 is a factor of p(x)
is a factor of p(x)
To find the other factors, we have to divide p(x) by x2 − 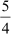 as follows:
as follows:
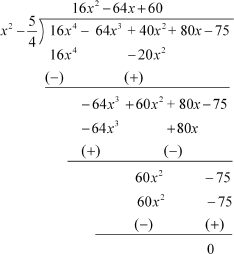
Now, 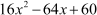 is the factor of p(x).
is the factor of p(x).
So, we can write 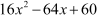 =
=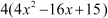
=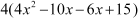 (Splitting the middle term)
(Splitting the middle term)
=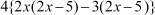
=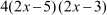
To find the zeroes, put 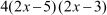 = 0
= 0
We have 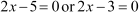
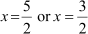
Thus, the remaining zeroes of the polynomial are x =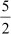 and
and 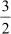 .
.

 ACERISE INDIA
ACERISE INDIA
