- Books Name
- Mathematics Book for CBSE Class 10
- Publication
- Carrier Point
- Course
- CBSE Class 10
- Subject
- Mathmatics
Euclid’s Division Lemma
Consider the following folk puzzle.
A trader was moving along a road selling eggs. An idler who didn’t have
much work to do, started to get the trader into a wordy duel. This grew into a
fight, he pulled the basket with eggs and dashed it on the floor. The eggs broke.
The trader requested the Panchayat to ask the idler to pay for the broken eggs.
The Panchayat asked the trader how many eggs were broken. He gave the
following response:
If counted in pairs, one will remain;
If counted in threes, two will remain;
If counted in fours, three will remain;
If counted in fives, four will remain;
If counted in sixes, five will remain;
If counted in sevens, nothing will remain;
My basket cannot accommodate more than 150 eggs.
So, how many eggs were there? Let us try and solve the puzzle. Let the number
of eggs be a. Then working backwards, we see that a is less than or equal to 150:
If counted in sevens, nothing will remain, which translates to a = 7p + 0, for
some natural number p. If counted in sixes, a = 6q+5, for some natural number q.
If counted in fives, four will remain. It translates to a = 5w + 4, for some natural
number w.
If counted in fours, three will remain. It translates to a = 4s + 3, for some natural
number s.
If counted in threes, two will remain. It translates to a = 3t + 2, for some natural
number t.
If counted in pairs, one will remain. It translates to a = 2u + 1, for some natural
number u.
That is, in each case, we have a and a positive integer b (in our example,
b takes values 7, 6, 5, 4, 3 and 2, respectively) which divides a and leaves a remainder
r (in our case, r is 0, 5, 4, 3, 2 and 1, respectively), that is smaller than b. The
* This is modified form of a puzzle given in ‘Numeracy Counts!’ by A. Rampal, and others. moment we write down such equations we are using Euclid’s division lemma,
which is given in Theorem 1.1.
Getting back to our puzzle, do you have any idea how you will solve it? Yes! You
must look for the multiples of 7 which satisfy all the conditions. By trial and error
(using the concept of LCM), you will find he had 119 eggs.
In order to get a feel for what Euclid’s division lemma is, consider the following
pairs of integers:
17, 6; 5, 12; 20, 4
Like we did in the example, we can write the following relations for each such
pair:
17 = 6 × 2 + 5 (6 goes into 17 twice and leaves a remainder 5)
5 = 12 × 0 + 5 (This relation holds since 12 is larger than 5)
20 = 4 × 5 + 0 (Here 4 goes into 20 five-times and leaves no remainder)
That is, for each pair of positive integers a and b, we have found whole numbers
q and r, satisfying the relation:
a = bq + r, 0 £ r < b
Note that q or r can also be zero.
Why don’t you now try finding integers q and r for the following pairs of positive
integers a and b?
(i) 10, 3; (ii) 4, 19; (iii) 81, 3
Did you notice that q and r are unique? These are the only integers satisfying the
conditions a = bq + r, where 0 £ r < b. You may have also realised that this is nothing
but a restatement of the long division process you have been doing all these years, and
that the integers q and r are called the quotient and remainder, respectively.
A formal statement of this result is as follows:
Theorem 1.1 (Euclid’s Division Lemma): Given positive integers a and b,
there exist unique integers q and r satisfying a = bq + r, 0 £ r < b.
This result was perhaps known for a long time, but was first recorded in Book VII
of Euclid’s Elements. Euclid’s division algorithm is based on this lemma.

Euclid’s division algorithm is a technique to compute the Highest Common Factor
(HCF) of two given positive integers. Recall that the HCF of two positive integers a
and b is the largest positive integer d that divides both a and b.
Let us see how the algorithm works, through an example first. Suppose we need
to find the HCF of the integers 455 and 42. We start with the larger integer, that is,
455. Then we use Euclid’s lemma to get
455 = 42 × 10 + 35
Now consider the divisor 42 and the remainder 35, and apply the division lemma
to get
42 = 35 × 1 + 7
Now consider the divisor 35 and the remainder 7, and apply the division lemma
to get
35 = 7 × 5 + 0
Notice that the remainder has become zero, and we cannot proceed any further.
We claim that the HCF of 455 and 42 is the divisor at this stage, i.e., 7. You can easily
verify this by listing all the factors of 455 and 42. Why does this method work? It
works because of the following result.
So, let us state Euclid’s division algorithm clearly.
To obtain the HCF of two positive integers, say c and d, with c > d, follow
the steps below:
Step 1: Apply Euclid’s division lemma, to c and d. So, we find whole numbers, q and
r such that c = dq + r, 0 £ r < d.
Step 2: If r = 0, d is the HCF of c and d. If r ¹ 0, apply the division lemma to d and r.
Step 3: Continue the process till the remainder is zero. The divisor at this stage will be the required HCF.
This algorithm works because HCF (c, d) = HCF (d, r) where the symbol
HCF (c, d) denotes the HCF of c and d, etc.
Example 1: Use Euclid’s algorithm to find the HCF of 4052 and 12576.
Solution:
Step 1: Since 12576 > 4052, we apply the division lemma to 12576 and 4052, to get
12576 = 4052 × 3 + 420
Step 2: Since the remainder 420 ¹ 0, we apply the division lemma to 4052 and 420, to
get
4052 = 420 × 9 + 272
Step 3: We consider the new divisor 420 and the new remainder 272, and apply the division lemma to get
420 = 272 × 1 + 148
We consider the new divisor 272 and the new remainder 148, and apply the division lemma to get
272 = 148 × 1 + 124
We consider the new divisor 148 and the new remainder 124, and apply the division lemma to get
148 = 124 × 1 + 24
We consider the new divisor 124 and the new remainder 24, and apply the division lemma to get
124 = 24 × 5 + 4
We consider the new divisor 24 and the new remainder 4, and apply the division lemma to get
24 = 4 × 6 + 0
The remainder has now become zero, so our procedure stops. Since the divisor at this stage is 4, the HCF of 12576 and 4052 is 4.
Notice that 4 = HCF (24, 4) = HCF (124, 24) = HCF (148, 124) =
HCF (272, 148) = HCF (420, 272) = HCF (4052, 420) = HCF (12576, 4052).
Euclid’s division algorithm is not only useful for calculating the HCF of very
large numbers, but also because it is one of the earliest examples of an algorithm that
a computer had been programmed to carry out.
Remarks:
1. Euclid’s division lemma and algorithm are so closely interlinked that people often
call former as the division algorithm also.
2. Although Euclid’s Division Algorithm is stated for only positive integers, it can be
extended for all integers except zero, i.e., b ¹ 0. However, we shall not discuss this
aspect here.
Euclid’s division lemma/algorithm has several applications related to finding
properties of numbers. We give some examples of these applications below:
Example 2: Show that every positive even integer is of the form 2q, and that every
positive odd integer is of the form 2q + 1, where q is some integer.
Solution: Let a be any positive integer and b = 2. Then, by Euclid’s algorithm,
a = 2q + r, for some integer q ³ 0, and r = 0 or r = 1, because 0 £ r < 2. So,
a = 2q or 2q + 1.
If a is of the form 2q, then a is an even integer. Also, a positive integer can be
either even or odd. Therefore, any positive odd integer is of the form 2q + 1.
Example 3: Show that any positive odd integer is of the form 4q + 1 or 4q + 3, where
q is some integer.
Solution: Let us start with taking a, where a is a positive odd integer. We apply the
division algorithm with a and b = 4.
Since 0 £ r < 4, the possible remainders are 0, 1, 2 and 3.
That is, a can be 4q, or 4q + 1, or 4q + 2, or 4q + 3, where q is the quotient.
However, since a is odd, a cannot be 4q or 4q + 2 (since they are both divisible by 2).
Therefore, any odd integer is of the form 4q + 1 or 4q + 3.
Example 4: A sweet seller has 420 kaju barfis and 130 badam barfis. She wants to
stack them in such a way that each stack has the same number, and they take up the
least area of the tray. What is the number of that can be placed in each stack for this purpose?
Solution: This can be done by trial and error. But to do it systematically, we find
HCF (420, 130). Then this number will give the maximum number of barfis in each
stack and the number of stacks will then be the least. The area of the tray that is used
up will be the least.
Now, let us use Euclid’s algorithm to find their HCF. We have:
420 = 130 × 3 + 30
130 = 30 × 4 + 10
30 = 10 × 3 + 0
So, the HCF of 420 and 130 is 10.
Therefore, the sweet seller can make stacks of 10 for both kinds of barfi.
- Books Name
- Mr. Sudhanshu Sharma Mathematics Book
- Publication
- Success Academy
- Course
- CBSE Class 10
- Subject
- Mathmatics

Euclid's Division Lemma: An Introduction
According to Euclid’s Division Lemma if we have two positive integers a and b, then there exist unique integers q and r which satisfies the condition a = bq + r where 0 ≤ r < b.
The basis of the Euclidean division algorithm is Euclid’s division lemma. To calculate the Highest Common Factor (HCF) of two positive integers a and b we use Euclid’s division algorithm. HCF is the largest number which exactly divides two or more positive integers. That means, on dividing both the integers a and b the remainder is zero.

Let us now get into the working of this Euclidean algorithm.
Euclid’s Division Lemma Algorithm
Consider two numbers 78 and 980 and we need to find the HCF of these numbers. To do this, we choose the largest integer first, i.e. 980 and then according to Euclid Division Lemma, a = bq + r where 0 ≤ r < b;
980 = 78 × 12 + 44
Now, here a = 980, b = 78, q = 12 and r = 44.
Now consider the divisor 78 and the remainder 44, apply Euclid division lemma again.
78 = 44 × 1 + 34
Similarly, consider the divisor 44 and the remainder 34, apply Euclid division lemma to 44 and 34.
44 = 34 × 1 + 10
Following the same procedure again,
34 = 10 × 3 + 4
10 = 4 × 2 + 2
4 = 2 × 2 + 0
As we see that the remainder has become zero, therefore, proceeding further is not possible. Hence, the HCF is the divisor b left in the last step. We can conclude that the HCF of 980 and 78 is 2.
Let us try another example to find the HCF of two numbers 250 and 75. Here, the larger the integer is 250, therefore, by applying Euclid Division Lemma a = bq + r where 0 ≤ r < b, we have
a = 250 and b = 75
⇒ 250 = 75 × 3 + 25
By applying the Euclid’s Division Algorithm to 75 and 25, we have:
75 = 25 × 3 + 0
As the remainder becomes zero, we cannot proceed further. According to the algorithm, in this case, the divisor is 25. Hence, the HCF of 250 and 75 is 25.
Example
Example: Find the HCF of 81 and 675 using the Euclidean division algorithm.
Solution: The larger integer is 675, therefore, by applying the Division Lemma a = bq + r where 0 ≤ r < b, we have
a = 675 and b = 81
⇒ 675 = 81 × 8 + 27
By applying Euclid’s Division Algorithm again we have,
81 = 27 × 3 + 0
We cannot proceed further as the remainder becomes zero. According to the algorithm, in this case, the divisor is 27. Hence, the HCF of 675 and 81 is 27.
This algorithm has got many practical applications in finding the properties of numbers. There is a lot more left to learn in real numbers. Enrich your knowledge by visiting our website www.byjus.com and download BYJU’S-the learning app and learn anywhere.
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics


Chapter 1: Real Numbers
Euclids Division Lemma
What is a dividend? Let us understand it with the help of a simple example. Can you divide 14 by 6?
![]()
After division, we get 2 as the quotient and 2 as the remainder.
Thus, we can also write 14 as 6 × 2 + 2.
A dividend can thus be written as:
Dividend = Divisor × Quotient + Remainder
Can you think of any other number which, when multiplied with 6, gives 14 as the dividend and 2 as the remainder?
Let us try it out with some other sets of dividends and divisors.
(1) Divide 100 by 20: 100 = 20 × 5 + 0
(2) Divide 117 by 15: 117 = 15 × 7 + 12
(3) Divide 67 by 17: 67 = 17 × 3 + 16
Thus, if we have a dividend and a divisor, then there will be a unique pair of a quotient and a remainder that will fit into the above equation.
This brings us to Euclid’s division lemma.
If a and b are positive integers, then there exist two unique integers, q and r,
such that a = bq + r
This lemma is very useful for finding the H.C.F. of large numbers where breaking them into factors is difficult. This method is known as Euclid’s Division Algorithm.
Let us look at some more examples.
Example 1: Find the H.C.F. of 4032 and 262 using Euclid’s division algorithm.
Solution:
Step 1:
First, apply Euclid’s division lemma on 4032 and 262.
4032 = 262 × 15 + 102
Step 2:
As the remainder is non-zero, we apply Euclid’s division lemma on 262 and 102.
262 = 102 × 2 + 58
Step 3:
Apply Euclid’s division lemma on 102 and 58.
102 = 58 × 1 + 44
Step 4:
Apply Euclid’s division lemma on 58 and 44.
58 = 44 × 1 + 14
Step 5:
Apply Euclid’s division lemma on 44 and 14.
44 = 14 × 3 + 2
Step 6:
Apply Euclid’s division lemma on 14 and 2.
14 = 2 × 7 + 0
In the problem given above, to obtain 0 as the remainder, the divisor has to be taken as 2. Hence, 2 is the H.C.F. of 4032 and 262.
Note that Euclid’s division algorithm can be applied to polynomials also.
Example 2: A rectangular garden of dimensions 190 m × 60 m is to be divided in square blocks to plant different flowers in each block. Into how many blocks can this garden be divided so that no land is wasted?
Solution:
If we do not want to waste any land, we need to find the largest number that completely divides both 190 and 60 and gives the remainder 0, i.e., the H.C.F. of (190, 60).
To find the H.C.F., let us apply Euclid’s algorithm.
190 = 60 × 3 + 10
60 = 10 × 6 + 0
Therefore, the H.C.F. of 190 and 60 is 10.
Therefore, there will be![]()
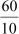
Hence, the total number of blocks in the garden will be 19 × 6 = 114.
Example 3: Find the H.C.F. of 336 and 90 using Euclid’s division algorithm.
Solution:
As 336 > 90, we apply the division lemma to 336 and 90.
336 = 90 × 3 + 66
Applying Euclid’s division lemma to 90 and 66: 90 = 66 × 1 + 24
Applying Euclid’s division lemma to 66 and 24:
66 = 24 × 2 + 18
Applying Euclid’s division lemma to 24 and 18:
24 = 18 × 1 + 6
Applying Euclid’s division lemma to 18 and 6:
18 = 6 × 3 + 0
As the remainder is zero, we need not apply Euclid’s division lemma anymore. The divisor (6) is the required H.C.F.
Example 4: Find the H.C.F. of 45, 81, and 117 using Euclid’s division algorithm.
Solution:
Let us begin by choosing any two out of the three given numbers, say 45 and 81. As 81 > 45, we apply Euclid’s division lemma to 81 and 45.
81 = 45 × 1 + 36
Applying Euclid’s division lemma to 45 and 36:
45 = 36 × 1 + 9
Applying Euclid’s division lemma to 36 and 9:
36 = 9 × 4 + 0
As the remainder is zero, the H.C.F. of 45 and 81 is 9.
Now, we again need to apply Euclid’s division algorithm on the H.C.F. of the two numbers and the remaining number.
Since the H.C.F. of 45 and 81 is 9 and the third number is 117, we apply Euclid’s division lemma to 117 and 9.
117 = 9 × 13 + 0
As the remainder is zero, the H.C.F. of 9 and 117 is 9.
Here, the second H.C.F. (the H.C.F. of the H.C.F. of the first two numbers and the third number) is the H.C.F. of the three numbers.
Thus, we can say that the H.C.F. of the three numbers is 9.
Example 5: In an inter-school essay writing competition, the numbers of participants from schools A, B, and C are 20, 16, and 28 respectively. If the participants in each room are from the same school, then find the minimum number of rooms required such that each room has the same number of participants.
Solution:
If we need to find the minimum number of rooms, then we need to keep the maximum number of participants in each room i.e., we need to find the largest number that completely divides 20, 16, and 28.
Thus, we start by choosing any two out of the given three numbers, say 20 and 16. Applying Euclid’s division lemma to 20 and 16:
20 = 16 × 1 + 4
Applying Euclid’s division lemma to 16 and 4:
16 = 4 × 4 + 0
Hence, 4 is the H.C.F. of 20 and 16.
Applying Euclid’s division algorithm to 28 and 4:
28 = 4 × 7 + 0
Hence, 4 is the H.C.F. of 28 and 4.
∴H.C.F. of 20, 16, 28 = 4
Therefore, each room would have 4 participants.
The number of rooms in which the participants from schools A, B, and C can be
accommodated is 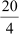
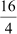
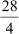
Therefore, a total of 5 + 4 + 7 =16 rooms are required.
The Use Of Euclids Division Lemma To Prove Mathematical Relationships
We can thus write this rule about the dividend as
This expression is unique, i.e., whenever we divide an integer (dividend) by another integer (divisor), we always get a fixed quotient and a fixed remainder.
The above statement can be proven by taking an example.
Whenever we divide 54 by 11, we will get 4 as the quotient and 10 as the remainder. We will never get a quotient other than 4 and a remainder other than 10 when we divide 54 by 11.
This brings us to Euclid’s division lemma.

This lemma has several applications, one of which is to prove mathematical relationships among numbers.
Let us discuss this concept with the help of a few examples.
Example 1: Prove that every positive integer is of the form 3p, 3p + 1, or 3p + 2, where p is any integer.
Solution:
Let a be any positive integer and let b = 3.
Applying Euclid’s algorithm to a and 3:
a = 3p + r; for some integer p and 0 ≤ r < 3
Therefore, a can be 3p, 3p + 1, or 3p + 2.
As a is a positive integer, we can say that any positive integer is of the form 3p, 3p + 1, or 3p + 2.
Example 2: Prove that every positive even integer is of the form 2m and every positive odd integer is of the form 2m + 1, where m is any integer.
Solution:
Let a be any positive integer and let b = 2.
According to Euclid’s division lemma, there exist two unique integers m and r such that
a = bm + r = 2m + r, where 0 ≤ r < 2. Thus, r = 0 or 1
If r = 0, i.e., if a = 2m, then the expression is divisible by 2. Thus, it is an even number.
If r = 1, i.e., if a = 2m + 1, then the expression is not divisible by 2. Thus, it is an odd number.
Thus, every positive even integer is of the form 2m and every positive odd integer is of the form 2m + 1.
Example 3: Prove that the expression y(y + 1) always represents an even number, where y is any positive integer.
Solution:
Let y be an integer. Thus, it may be either odd or even.
When y is an odd number, i.e., when y is of the form 2p + 1, where p is an integer:
y(y + 1) = (2p + 1)(2p + 1 + 1) = (2p + 1)(2p + 2) = 2(2p + 1)(p + 1)
The above expression is a multiple of 2. Thus, the expression y(y + 1) represents an even number.
When y is an even number, i.e., when y is of the form 2q, where q is an integer:
y(y + 1) = (2q)(2q + 1) = 2q(2q + 1)
The above expression is a multiple of 2. Thus, the expression y(y + 1) represents an even number.
Thus, for a positive integer y, the expression y(y + 1) always represents an even number.
Example 4:
Show that
(a) The sum, the difference, and the product of two even numbers is always even.
(b) The sum and the difference of two odd numbers is always even, whereas their product is always odd.
Solution:
(a) Let there be two even numbers, x and y, such that x = 2m and y = 2n, where m and n are two positive integers.
Now, x + y = 2m + 2n = 2(m + n) = 2p, where p = m + n is an integer. Thus, x + y is always even.
Similarly, x − y = 2m − 2n = 2(m − n) = 2q, where q = m − n is an integer. Thus, x − y is always even.
Likewise, xy = 2m × 2n = 4mn = 2(2mn) = 2t, where t = 2mn is an integer. Thus, xy is always even.
Hence, the sum, the difference, and the product of two even numbers is always even.
(b) Let there be two odd numbers x and y such that x = 2m + 1 and y = 2n + 1, where m and n are two positive integers.
Now, x + y = (2m + 1) + (2n + 1) = 2(m + n + 1) = 2p, where p = m + n + 1 is an integer. Thus, x + y is even.
Similarly, x − y = (2m + 1) − (2n + 1) = 2(m − n) = 2q, where q = m − n is an integer.
Thus, x − y is even.
Likewise, xy = (2m + 1)(2n + 1) = 2(2mn + m + n) + 1 = 2t + 1, where t = 2mn + m + n is an integer.
Thus, xy is always odd.
Hence, the sum and the difference of two odd numbers is always even, whereas their product is always odd.
- Books Name
- Sample paper Term II Maths
- Publication
- SonikaAnandAcademy
- Course
- CBSE Class 10
- Subject
- Mathmatics

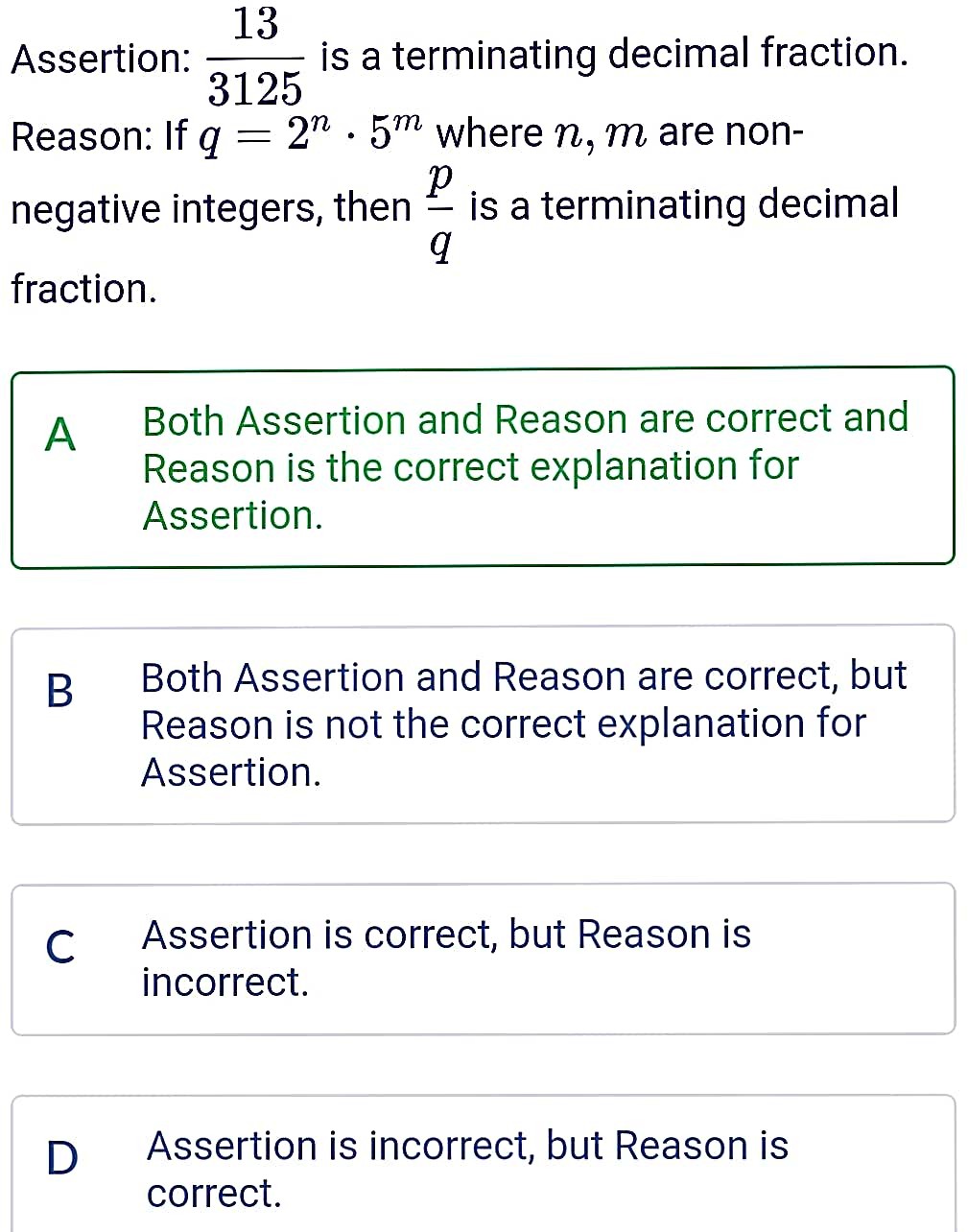

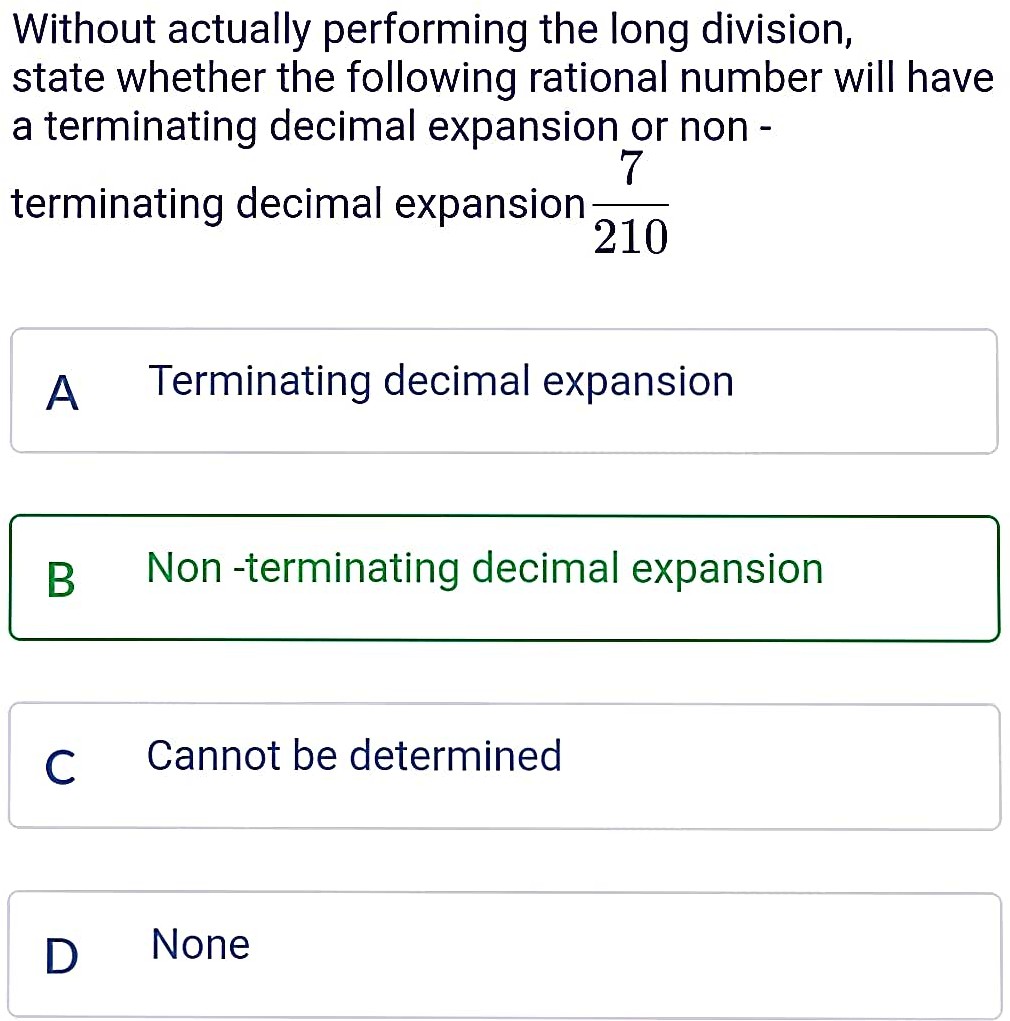







Sample

 Carrier Point
Carrier Point
 Success Academy
Success Academy
 ACERISE INDIA
ACERISE INDIA


