Chapter 4: Quadratic equations

Introduction to Quadratic Equations

Consider the equations

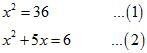
In equation (1), variable occurs only in second degree. The quadratic equations involving a variable only in second degree is a Pure quadratic equation.

Thus, an equation that can be expressed in the form 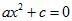, where a and c are real numbers and a ≠ 0 is a pure quadratic equation.

In equation (2) , variable occurs both in second and first degree. The quadratic equation involving a variable in both second and first degree is an Adfected quadratic equation.

Thus, an equation that can be expressed in the form 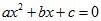, where a, b and c are real numbers and a ≠ 0 is an Adfected quadratic equation.

Now, let us learn about the roots of a quadratic equation.

Roots of a given quadratic equation are the values of the variables which satisfy that quadratic equation.

For example, consider the quadratic equation x² – 8x + 15 = 0. Here, L.H.S. = x2 – 8x + 15 and R.H.S. = 0

Let us substitute the different values of variable x in this equation and observe the results. When x = 1 then x² – 8x + 15 = 12 – 8(1) + 15 = 1 – 8 + 15 = 8 ∴ L.H.S. ≠ R.H.S.

When x = –1 then x² – 8x + 15 = (–1)² – 8(–1) + 15 = 1 + 8 + 15 = 24 ∴ L.H.S. ≠ R.H.S.

When x = 3 then x² – 8x + 15 = 3² – 8(3) + 15 = 9 – 24 + 15 = 0 ∴ L.H.S. = R.H.S.

When x = 4 then x² – 8x + 15 = 4² – 8(4) + 15 = 16 – 32 + 15 = –1 ∴ L.H.S. ≠ R.H.S.

When x = 5 then x² – 8x + 15 = 5² – 8(5) + 15 = 25 – 40 + 15 = 0 ∴ L.H.S. = R.H.S.

When x = –5 then x² – 8x + 15 = (–5)² – 8(–5) + 15 = 25 + 40 + 15 = 80 ∴ L.H.S. ≠ R.H.S.

It can be observed that for x = 3 and x = 5, we have L.H.S. = R.H.S. which means that the equation x² – 8x + 15 = 0 is satisfied. Thus, 3 and 5 are roots of this quadratic equation.

In other words, we can say that x = 3 and x = 5 are the solutions of quadratic equation x² – 8x + 15 = 0.

Also, for x = 1, x = –1, x = 4 and x = –5, we have L.H.S. ≠ R.H.S. which means that the equation x² – 8x + 15 = 0 is not satisfied. Thus, 1, –1, 4 and –5 are not the roots or solution of this quadratic equation.

Let us go through few examples to understand the concept better.

Example 1: Is the equation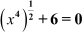 a quadratic equation?

Solution:

The given equation is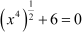

We can also write it as

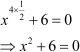
Hence, we can say that the given equation is a quadratic equation.

Example 2: Among the values given below find the roots of the quadratic equation 2x2 + 5x – 3 = 0.

x = 1, 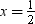, x = 2, x = –3,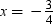

Solution:

We have,

Equation: 2x² + 5x – 3 = 0

Values: x = 1, 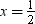, x = 2, x = –3,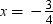

Let us substitute the given values of x in the equation and observe the results. When x = 1 then 2x² + 5x – 3 = 2(1)² + 5(1) – 3 = 2 + 5 – 3 = 4 ∴ L.H.S. ≠ R.H.S.

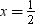When then

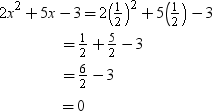
∴ L.H.S. = R.H.S.

When x = 2 then 2x² + 5x – 3 = 2(2)² + 5(2) – 3 = 8 + 10 – 3 = 15 ∴ L.H.S. ≠ R.H.S.

When x = –3 then 2x² + 5x – 3 = 2(–3)² + 5(–3) – 3 = 18 – 15 – 3 = 0 ∴ L.H.S. = R.H.S.

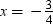When then

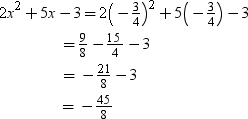
∴ L.H.S. ≠ R.H.S.

Only, 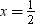and x = –3 satisfy the given quadratic equation.

Thus, 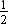and –3 are the roots of the given quadratic equation.

Example 3: If one root of the quadratic equation 3x² + 4x – p = 0 is 2323 then find the value of p.

Solution:

Since 2323 is a root of the equation 3x² + 4x – p = 0, it must satisfy the equation.

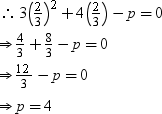
Example 4: State whether m is a root of the equation 2x² – (2m + 3)x + 3m = 0 or not.

Solution:

If m is a root of the equation 2x² – (2m + 3)x + 3m = 0 then it would satisfy the equation. Let us check it by substituting x = m in the given equation

2m² – (2m + 3)m + 3m

= 2m² – 2m² – 3m + 3m

= 0

∴ L.H.S. = R.H.S.

Hence, m is a root of the equation 2x² – (2m + 3)x + 3m = 0.

Expressing Given Situations as Quadratic Equations in One Variable

Quadratic equations arise in several situations around us and in different fields of mathematics. But how is a quadratic equation formulated?

Let us learn to express a situation mathematically.

Suppose there are two squares as shown in the following figure.

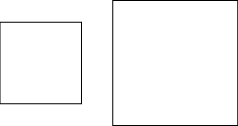
The sum of the areas of these two squares is 482 m² and the difference of their perimeters is 32 m. Can we form a quadratic equation for the given mathematical situation?

Example1: An express train takes 1 hour less than a passenger train to travel a distance of 132 km. If the average speed of the express train is 11 km/h more than that of a passenger train, then form a quadratic equation to find the average speed of the express train?

Solution:

Let the average speed of the express train be x km/h.

Since it is given that the speed of the express train is 11 km/h more than that of a passenger train,

Therefore, the speed of the passenger train will be x −11 km/h. Also we know that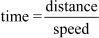

Time taken by the express train to cover 132 km =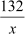

Time taken by the passenger train to cover 132 km =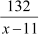

And the express train takes 1 hour less than the passenger train. Therefore,

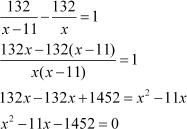
This is the required quadratic equation.

Example 2: A chess board contains 64 equal squares and the area of each square is 6.25 cm². A border 2 cm wide is made around the board. Formulate a quadratic equation to find the length of each side of the board?

Solution:

Let the length of each side of the chess board be x cm.

Therefore, the length of the chess board without border will be x − 4 cm as shown in the following figure.

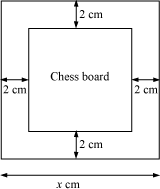
Area of the chess board without border = (x − 4)²

It is given that the area of each square is 6.25 cm².

Area of 64 squares on the chess board = 6.25 × 64

Therefore,

(x − 4)2 = 64 6.25

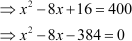
This is the required quadratic equation.

Solution of Quadratic Equations by the Method of Factorization

Quadratic equations come from many real life situations. Let us consider one such situation.

The area of a rectangular garden is 500 m² and its length is 5 m more than its breadth. Can we find the length and breadth of the garden?

The garden can be drawn as

Let the breadth of the garden be x m.

Then, according to the given information, its length must be (x + 5) m.

Now, area of the garden = length × breadth = (x + 5) × x

The area of the garden is given as 500 m².

∴ (x + 5) × x = 500

We can rewrite this equation as

x² + 5x = 500

⇒ x² + 5x – 500 = 0

This is a quadratic equation in variable x.

The length and the breadth of the garden can be calculated by solving the given quadratic equation.

How do we solve a quadratic equation? There are three methods of solving a quadratic equation, one of which is the method of factorization.

We have now expressed the equation x² + 5x – 500 = 0 as the product of two factors, (x + 25) and (x – 20). We can find the solutions of this equation by equating each factor to 0.

∴ x + 25 = 0 and x – 20 = 0

⇒ x = –25 and x = 20

However, the breadth of a park cannot be negative.

∴ x = 20

Thus, breadth of the park = 20 m and length of the park = (20 + 5) m = 25 m.

Let us now look at some more examples to get a grasp on this concept.

Example 1: Find the roots of the equation .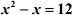

Solution:

First, we rearrange the given equation according to the standard format.

x² – x = 12

⇒ x² – x – 12 = 0

We need a pair of numbers whose product is –12 and whose sum is –1.

These numbers are 3 and –4.

We can now rewrite the equation as

x² – x – 12 = 0

⇒ x² + 3x – 4x – 12 = 0

⇒ x(x + 3) – 4(x + 3) = 0

⇒ (x – 4)(x + 3) = 0

The solutions of the given equation can now be determined by equating the two factors to 0.

∴ (x – 4) = 0 and (x + 3) = 0

⇒ x = 4 and x = –3

Thus, the two roots of the quadratic equation are 4 and –3.

Example 2: Find the roots of the equation .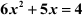

Solution:

First, we rearrange the given equation according to the standard format.

6x² + 5x – 4 = 0

Here, we need to find two such numbers whose product is 6 × (–4) = –24 and whose sum is 5.

The required numbers are 8 and –3.

Now, [8 × (–3) = –24 and 8 + (–3) = 5]

6x² + 5x – 4 = 0

⇒ 6x² + 8x –3x – 4 = 0

⇒ 2x(3x + 4) – 1(3x + 4) = 0

⇒ (2x – 1)(3x + 4) = 0

⇒ 2x – 1 = 0 and 3x + 4 = 0

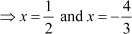
Thus, the roots of the given equation are .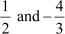

Example 3: Find two positive consecutive odd integers whose product is 99.

Solution:

Let the first integer be x.

The next odd integer will thus be x + 2.

∴ x(x + 2) = 99

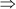x² + 2x – 99 = 0

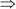x² + 11x – 9x – 99 = 0

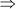x(x + 11) – 9(x + 11) = 0

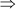(x – 9)(x + 11) = 0

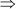x – 9 = 0 and x + 11 = 0

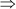x = 9 and x = –11

However, we know that the two integers are positive.

∴ x = 9

Thus, the two integers are 9 and (9 + 2) = 11.

Example 4: The width of a rectangle is 16 feet less than 3 times its length. If the area of the rectangle is 35 ft², then what are the dimensions of the rectangle?

Solution:

Here, the width of the rectangle has been expressed in terms of its length.

Hence, let us take the length of the rectangle to be x.

Thus, width of the rectangle = 3x – 16

The area of the rectangle is 35 ft².

∴ 35 = x(3x –16)

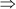35 = 3x² – 16x

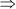3x² – 16x – 35 = 0

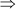3x² – 21x + 5x – 35 = 0

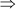3x(x – 7) + 5(x – 7) = 0

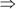(3x + 5)(x – 7) = 0

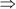3x + 5 = 0 and x – 7 = 0

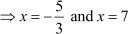
However, the length of a rectangle cannot be negative.

∴ x = 7

Thus, length of the rectangle is x = 7 ft and the width of the rectangle is 3x – 16 = (3 × 7 – 16) ft = 5 ft

Example 5: Difference between the ages of a father and his son is 22 years. If the product of their ages is 555 then what are their ages?

Solution:

Let the age of the son be x years.

Then age of the father will be 22 + x years.

Since the product of their ages is 555, we have

x(22 + x) = 555

⇒22x + x² = 555

⇒x² + 22x – 555 = 0

⇒x² + 37x – 15x – 555 = 0

⇒x(x + 37) – 15(x + 37) = 0

⇒(x + 37) (x – 15) = 0

⇒(x + 37) = 0 or (x – 15) = 0

⇒x = –37 or x = 15

Age cannot be negative, so we consider x = 15.

∴ Age of son = 15 years

∴ Age of father = (22 + 15) years = 37 years

Example 6: A bus takes 3 hours more than a train to travel a distance of 770 km. The speed of the train is more than that of bus by 15 km/hr. What are the average speeds of the bus and train?

Solution:

Let the average speed of the bus be x km/hr.

Then the average speed of the train will be (x + 15) km/hr.

Time taken by bus to cover 770 km =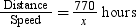

 Time taken by train to cover 770 km =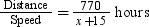

According to the question, we have

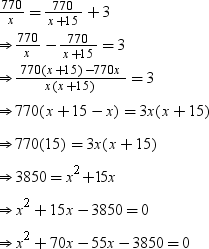
⇒ x(x + 70) – 55(x + 70) = 0

⇒ (x + 70) (x – 55) = 0

⇒ (x + 70) = 0 or (x – 55) = 0

⇒ x = –70 or x = 55

Speed cannot be negative, so we will consider x = 55.

∴ Average speed of bus = 55 km/hr

∴ Average speed of train = (55 + 15) km/hr = 70 km/hr

Solution of Quadratic Equations by Completing Squares

Many real life situations can result in quadratic equations. For example, consider the following situation:

A ladder is leaning against a wall. The top of the ladder touches the wall at a

height of 15 feet. The length of the ladder is one foot more than twice its distance from the foot of the wall. We need to find the length of the ladder.

We can express the given situation mathematically with the help of a quadratic equation.

Let us see how.

Let the distance from the wall to the bottom of the ladder be x feet.

It is given that the length of the ladder is one foot more than twice its distance from the foot of the wall.

Hence, the length of the ladder becomes (2x + 1).

The wall makes an angle of 90° with respect to the ground. Since the ladder is leaning against the wall, the entire arrangement forms a right triangle in which the ladder acts as the hypotenuse.

On applying Pythagoras theorem, we get

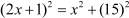
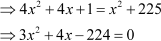
Now, to find the length of the ladder, we first need to solve the given quadratic equation. Observe that if you try to solve it by splitting the middle term, then it will become very lengthy. In such cases, it is easier to solve the quadratic equation by another method called the Completion of Squares.

Let us learn this method with the help of an example. Consider the following quadratic equation:

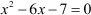
In this method, we need to convert the quadratic equation in the form

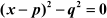
To convert a quadratic equation in this form, we will make use of the following identities:

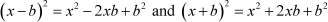
In the example taken previously, the given equation was .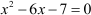

Note that the term with the coefficient x has a negative sign attached to it.

We thus need to make use of the identity 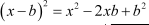here.

On comparing this equation with the given identity, we get 2b = 6, i.e., b = 3.

Thus, we need to add 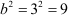on both sides of the equation.

The equation now becomes .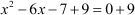

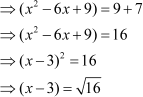
It is important to remember that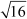 has two values, i.e., 4 and –4.

Thus, the equation can be further simplified as

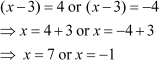
Thus, the given equation has two solutions, i.e., x = 7 and x = –1.

Let us now go back to the initial problem we were discussing.

We had arrived at a final quadratic equation, which was .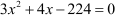

Note that in this case, the term with the coefficient x² is not a perfect square. We thus need to multiply the equation by 3 to make it a perfect square.

On doing so, we get

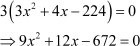
The identity can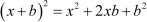 be used here.

The equation can now be solved as

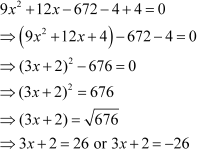
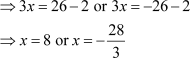
However, x represents the distance of the foot of the ladder from the base of the wall, which cannot be negative. Thus, x has only one value, i.e., 8.

Thus, length of the ladder = 2x + 1 = (2 × 8 + 1) ft = 17 ft

We can follow one more approach to solve this equation.

The equation was .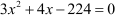

Here, the term with the coefficient x² is not a perfect square. We thus convert it to a perfect square by multiplying the equation by 3.

Note that we could also have divided the equation by 3 and still have converted the term to a perfect square.

Let us see how.

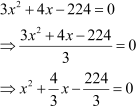
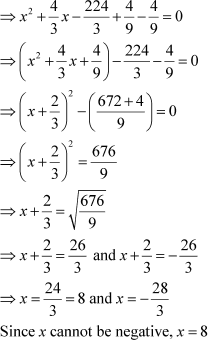
We can use any of the two methods mentioned above, as long as we covert the equation to the form .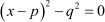

Note: Usually, the roots of the quadratic equation ,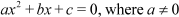can be found by first dividing the equation by and then completing the squares of the terms in the equation.

Example 1: Find the roots of the equation 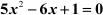 by the method of completion of squares.

Solution:

The given equation is .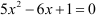

By multiplying the equation by 5, we get .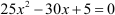

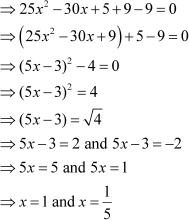
Example 2: Find the roots of the equation 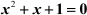 by the method of completion of squares.

Solution:

The given equation is .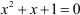

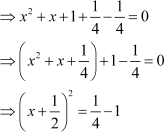
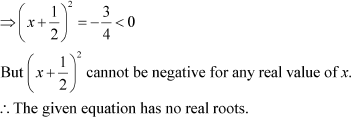
Example 3: Find three consecutive even integers so that the product of the first two numbers is three times the third number.

Solution:

Let the three numbers be x, (x + 2), and (x + 4).

From the given condition, we have x(x + 2) = 3(x + 4).

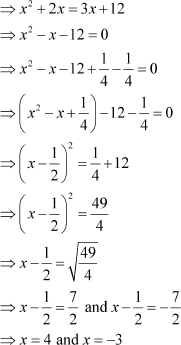
However, the three numbers are positive integers.

Thus, x cannot be equal to –3.

Thus, the three consecutive even integers are 4, 6, and 8.

Example 4: Denominator of a fraction is 3 more than its numerator such that both are positive integers. If the sum of the fraction and its reciprocal is 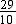then find the fraction.

Solution:

Let the numerator be x. Then the denominator will be x + 3.

According to the question, we have

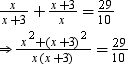
⇒ 10(x2 + x2 + 6x + 9) = 29x(x + 3)

⇒ 20x2 + 60x + 90 = 29x2 + 87x

⇒ 9x2 + 27x – 90 = 0

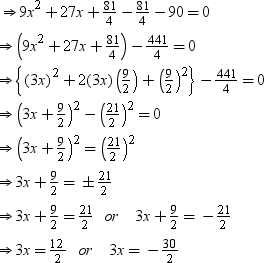
⇒ x = 2 or x = –5

–5 is a negative integer, so it is discarded.

Consider x = 2

∴ Numerator = 2 and Denominator = 2 + 3 = 5

∴ Fraction =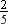

Example 5: Base of a small triangular garden is 7 m more than its height. If the area of the garden is 60 m² then find its base and height.

Solution:

Let the height of the triangular garden be x m. Then its base will be (x + 7) m.

Area of triangular garden =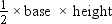

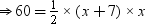
⇒120 = x2 + 7x

⇒ x2 + 7x – 120 = 0

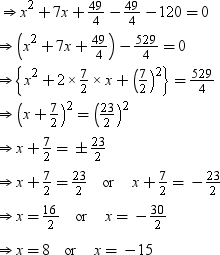
Length cannot be negative, so we consider x = 8.

∴ Height of triangular garden = 8 m

∴ Base of triangular garden = (8 + 7) m = 15 m

Solution of Quadratic Equations by Using Quadratic Formula

The following equations are quadratic in nature:

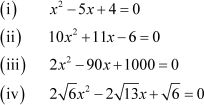
If we were to solve these equations, we could have either factorized the equations (i), (ii), and (iii) or completed their squares.

However, note that we would face a lot of difficulty in solving equation (iv) by either of these two methods.

Apart from factorizing a quadratic equation or completing its square, we can also use the quadratic formula to factorize an equation.

Let us go back to equation (iv), which was 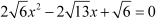. Comparing this equation with the general form of a quadratic equation:

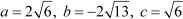
Thus, according to the quadratic formula:

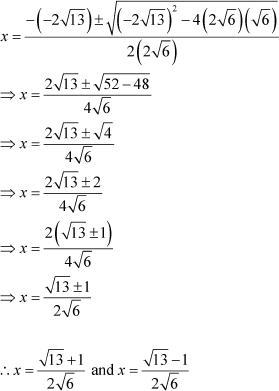
Let us now solve some more quadratic equations by using the quadratic formula.

Example 1: Solve the quadratic equation 5x² + x− 22 = 0 by using the quadratic formula.

Solution:

On comparing the given equation with the general form ax² + bx + c = 0, we get

a = 5, b = 1, c = −22

On putting these values in the quadratic formula, we get

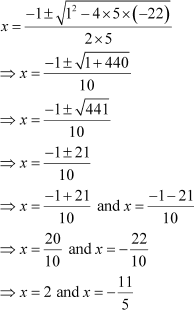
Example 2: Find the roots of the equation 3x² + 5x + 10 = 0 by using the quadratic equation formula.

Solution:

On comparing the given equation with the general form ax² + bx + c = 0, we get

a = 3, b = 5, c = 10

∴ b² − 4ac = (5⁾² − 4 × 3 × 10

= 25 − 120

= −95 <</span> 0

Thus, 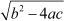does not have any real value.

Thus, there are no real roots for the given equation.

Example 3: The denominator of a fraction is 2. If the sum of the fraction and its

reciprocal is , then find the fraction.

Solution:

Let the numerator of the fraction be x.

Hence, the rational number is .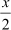

It is given that the sum of the fraction and its reciprocal is .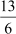

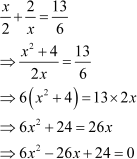
On comparing this equation with the general form ax² + bx + c = 0, we get

a = 6, b = −26, c = 24

On putting these values in the quadratic formula, we get

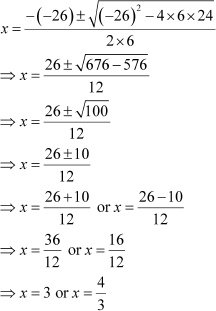
Since x is the numerator of the fraction, it has to be an integer.

∴ x = 3

Thus, the fraction is .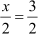

Example 4: The perimeter of a rectangle is 34 cm and its area is 70 cm². Find the length and the breadth of the rectangle.

Solution:

Let the length and breadth of the rectangle be x and y respectively.

Thus, perimeter of the rectangle = 2(x + y) = 34 cm

⇒ x + y = 17

⇒ y = 17 – x … (1)

Thus, area of the rectangle = x × y = 70 cm² … (2)

Substituting the value of y from (1) in (2):

x(17 – x) = 70

⇒ 17x – x² = 70

⇒ x² – 17x + 70 = 0

By using the quadratic formula, we get

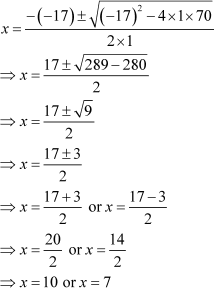
Thus, the length and the breadth of the rectangle are 10 cm and 7 cm respectively.

Example 5: A ball is thrown upwards from a height of 6 m with a particular speed. The height h of the ball after t seconds is given by 6 + 13t – 5t². How long the ball will take to touch the ground?

Solution:

Height of the ball after t seconds is given as follows:

h = 6 + 13t – 5t²

When ball will touch the ground, the height will be 0 m.

⇒ 0 = 6 + 13t – 5t²

⇒ 5t² – 13t – 6 = 0

By using the quadratic formula, we get

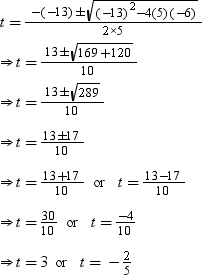
Time cannot be negative, so we will consider t = 3.

Thus, the ball will touch the ground after 3 seconds.

Example 6: A super fast train takes 6 hours less than a passenger train to reach the destination which is 1440 km away. If the speed of the super fast train is 40 km/hr more than that of passenger train then find the average speed of both trains.

Solution:

Let the average speed of passenger train be x km/hr.

Then the average speed of super fast train will be x + 40 km/hr.

Total distance to be covered = 1440 km

Total time taken by passenger train =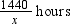

Total time taken by super fast train =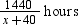

According to the question, we have

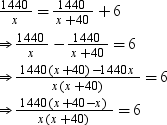
⇒ 1440(40) = 6x(x + 40)

⇒ x² + 40x – 9600 = 0

By using the quadratic formula, we get

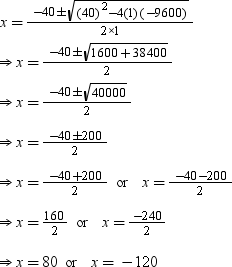
Speed cannot be negative, so we consider x = 80.

∴ Average speed of passenger train = 80 km/hr

∴ Average speed of super fast train = (80 + 40) km/hr = 120 km/hr

Conditions Under which a Quadratic Equation has Real or Imaginary Roots

A right angled ΔABC is given in the following figure.

In this triangle, the base BC is 5 cm less than twice its height AB. The hypotenuse of the triangle is 2 cm.

Is the above given situation possible for triangle ΔABC?

Can we also find the nature of roots of a quadratic equation without solving the equation?

We can see from the above example that the value of x depends on the value under the sign of square root. If this value is positive, then the value of x will be real and if it is negative, the value of x will be imaginary.

Thus, we can say that the nature of the values of x in quadratic equation ax² + bx + c = 0, depends on the value of b² − 4ac.

Here, b² − 4ac is called the discriminant of the quadratic equation ax² + bx + c = 0. The value of b² − 4ac determines the nature of the roots of a quadratic equation.

For example: The quadratic equation 3x² − x + 2 = 0 has no real root because for this equation,

b² − 4ac = (−1)² − 4 × 3 × 2

= 1 − 24

= − 23 < 0

Here b² − 4ac < 0.

Thus, the equation 3x² − x + 2 = 0 has no real roots.

Now, let us solve some more examples based on the natures of roots of quadratic equations.

Example 1: Find the value of discriminant for the quadratic equation x² + 4x − 21 = 0.

Solution:

The given quadratic equation is x² + 4x − 21 = 0.

On comparing this equation with the standard form of quadratic equation, ax² + bx + c = 0,

we have

a = 1, b = 4, c = − 21

Therefore, the discriminant, b² − 4ac = (4)² − 4 × 1 × (− 21)

= 16 + 84

= 100

Thus, the value of discriminant for the given quadratic equation is 100.

Example 2: Find the nature of the roots of quadratic equation, x² − 8x + 16 = 0.

Solution:

The given equation is x² − 8x + 16 = 0.

On comparing this equation with the standard form of quadratic equation, ax² + bx + c = 0, we have a = 1, b = − 8, c = 16.

Therefore, the discriminant,

b² − 4ac = (− 8)² − 4 × 1 × 16

⇒ b² − 4ac = 64 − 64

⇒ b² − 4ac = 0

Thus, the given quadratic equation has two equal real roots.

Example 3: Find the value of k for which the quadratic equation x² − 12x + k = 0 has two real equal roots.

Solution:

On comparing the given equation with ax² + bx + c = 0, we have a = 1, b = − 12, c = k

For two real equal roots,

b² − 4ac = 0

⇒ (− 12)² − 4 × 1 × k = 0

⇒ 144 − 4k = 0

⇒ 4k = 144

⇒ k = 36

Thus, the value of k is 36.

Example 4: Is it possible to design a rectangular garden whose area is 250 square m and the sum of whose length and breadth is 20 m?

Solution:

Let the length of the garden be x m.

∴ Breadth = (20 − x) m

Area of garden = length × breadth

250 = x × (20 − x)

⇒ 250 = 20x − x²

⇒ x² − 20x + 250 = 0

This is a quadratic equation whose discriminant is b² − 4ac = (− 20)² − 4 × 1 × 250

= 400 − 1000

= − 600 < 0

Therefore, the roots of the equation are not real. Hence, it is not possible to design such a garden.

Example 5: Can we find two consecutive positive numbers whose product is 420? If yes, then find the numbers.

Solution:

Let one number be x.

Then the other number = x + 1

According to the question,

x × (x + 1) = 420

⇒ x² + x = 420

⇒ x² + x − 420 = 0

The discriminant of this equation is b² − 4ac = (1)² − 4 × 1 × (− 420)

= 1 + 1680

= 1681

∴ b² − 4ac > 0

Therefore, the roots of the quadratic equation x² + x − 420 = 0 are real. We can find the numbers using quadratic formula as follows

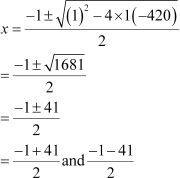
x = 20 and − 21

We take x = 20, as − 21 is a negative number.

Thus, 20 and 21 are the two consecutive positive numbers whose product is 420.

Determination of roots

ax²+bx+c = 0 

discriminant =✓b²-4ac 

If discriminant is greater than 0 then roots are real and unequal

If discriminant is equal to zero roots are equal

If discriminant is less than zero roots are imaginary