2.Arithmetic Fundamental Theorem

The Fundamental Theorem of Arithmetic

In your earlier classes, you have seen that any natural number can be written as a

product of its prime factors. For instance, 2 = 2, 4 = 2 × 2, 253 = 11 × 23, and so on.

Now, let us try and look at natural numbers from the other direction. That is, can any

natural number be obtained by multiplying prime numbers? Let us see.

Take any collection of prime numbers, say 2, 3, 7, 11 and 23. If we multiply

some or all of these numbers, allowing them to repeat as many times as we wish,

we can produce a large collection of positive integers (In fact, infinitely many).

Let us list a few:

7 × 11 × 23 = 1771 3 × 7 × 11 × 23 = 5313

2 × 3 × 7 × 11 × 23 = 10626 23 × 3 × 73 = 8232

22 × 3 × 7 × 11 × 23 = 21252

and so on.

Now, let us suppose your collection of primes includes all the possible primes.

What is your guess about the size of this collection? Does it contain only a finite

number of integers, or infinitely many? Infact, there are infinitely many primes. So, if

we combine all these primes in all possible ways, we will get an infinite collection of

numbers, all the primes and all possible products of primes. The question is – can we

produce all the composite numbers this way? What do you think? Do you think that

there may be a composite number which is not the product of powers of primes?

Before we answer this, let us factorise positive integers, that is, do the opposite of

what we have done so far.

We are going to use the factor tree with which you are all familiar. Let us take

some large number, say, 32760, and factorise it as shown:

So, we have factorised 32760 as 2 × 2 × 2 × 3 × 3 × 5 × 7 × 13 as a product of

primes, i.e., 32760 = 23 × 32 × 5 × 7 × 13 as a product of powers of primes. Let us try

another number, say, 123456789. This can be written as 32 × 3803 × 3607. Of course,

you have to check that 3803 and 3607 are primes! (Try it out for several other natural

numbers yourself.) This leads us to a conjecture that every composite number can be

written as the product of powers of primes. In fact, this statement is true, and is called the Fundamental Theorem of Arithmetic because of its basic crucial importance to the study of integers. Let us now formally state this theorem.

Theorem 1.2 (Fundamental Theorem of Arithmetic): Every composite number

can be expressed (factorised) as a product of primes, and this factorisation is

unique, apart from the order in which the prime factors occur.

The Fundamental Theorem of Arithmetic says that every composite number

can be factorised as a product of primes. Actually it says more. It says that given

any composite number it can be factorised as a product of prime numbers in a

‘unique’ way, except for the order in which the primes occur. That is, given any

composite number there is one and only one way to write it as a product of primes,

as long as we are not particular about the order in which the primes occur. So, for

example, we regard 2 × 3 × 5 × 7 as the same as 3 × 5 × 7 × 2, or any other

possible order in which these primes are written. This fact is also stated in the

following form:

The prime factorisation of a natural number is unique, except for the order

of its factors.

In general, given a composite number x, we factorise it as x = p1 p 2 ... pn, where

p1

, p2

,..., pn are primes and written in ascending order, i.e., p1

£ p2

£ . . . £ p

n

. If we combine the same primes, we will get powers of primes. For example,

32760 = 2 × 2 × 2 × 3 × 3 × 5 × 7 × 13 = 23 × 32 × 5 × 7 × 13

Once we have decided that the order will be ascending, then the way the number

is factorised, is unique.

The Fundamental Theorem of Arithmetic has many applications, both within

mathematics and in other fields. Let us look at some examples.

Example 5: Consider the numbers 4n, where n is a natural number. Check whether

there is any value of n for which 4n ends with the digit zero.

Solution: If the number 4n, for any n, were to end with the digit zero, then it would be divisible by 5. That is, the prime factorisation of 4n would contain the prime 5.

not possible because 4n = (2)2n; so the only prime in the factorisation of 4n is 2. So, the

uniqueness of the Fundamental Theorem of Arithmetic guarantees that there are no

other primes in the factorisation of 4n. So, there is no natural number n for which 4n

ends with the digit zero.

You have already learnt how to find the HCF and LCM of two positive integers

using the Fundamental Theorem of Arithmetic in earlier classes, without realising it!

This method is also called the prime factorisation method. Let us recall this method

through an example.

Example 6: Find the LCM and HCF of 6 and 20 by the prime factorisation method.

Solution: We have: 6 = 21 × 31 and 20 = 2 × 2 × 5 = 22 × 51.

You can find HCF (6, 20) = 2 and LCM (6, 20) = 2 × 2 × 3 × 5 = 60, as done in your

earlier classes.

Note that HCF (6, 20) = 21 = Product of the smallest power of each common

prime factor in the numbers.

LCM (6, 20) = 22 × 31 × 51 = Product of the greatest power of each prime factor, involved in the numbers.

From the example above, you might have noticed that HCF (6, 20) × LCM (6, 20)

= 6 × 20. In fact, we can verify that for any two positive integers a and b,

HCF (a, b) × LCM (a, b) = a × b. We can use this result to find the LCM of two

positive integers, if we have already found the HCF of the two positive integers.

Example 7: Find the HCF of 96 and 404 by the prime factorisation method. Hence,

find their LCM.

Solution: The prime factorisation of 96 and 404 gives:

96 = 25 × 3, 404 = 22 × 101

Therefore, the HCF of these two integers is 22 = 4.

Also, LCM (96, 404) =

96 404 96 404

9696

HCF (96, 404) 4

Example 8: Find the HCF and LCM of 6, 72 and 120, using the prime factorisation

method.

Solution: We have:

6 = 2 × 3, 72 = 23 × 32, 120 = 23 × 3 × 5

Here, 21 and 31 are the smallest powers of the common factors 2 and 3, respectively.

So, HCF (6, 72, 120) = 21 × 31 = 2 × 3 = 6

23, 32 and 51 are the greatest powers of the prime factors 2, 3 and 5 respectively

involved in the three numbers.

So, LCM (6, 72, 120) = 23 × 32 × 51 = 360

Remark: Notice, 6 × 72 × 120 ¹ HCF (6, 72, 120) × LCM (6, 72, 120). So, the

product of three numbers is not equal to the product of their HCF and LCM.

Subject	Unit		Chapter		Day	Maximum Marks:
Zoology			Chemical Coordination and Integration		1	Negative Marks:
Type of Question:-	Single Choice		Multiple			Integer
Source:-
Information:-	Single Choice
Question:- 107	I. ACTH II. GH III. MSH IV. FSH V. LH VI. Oxytocin Which of the above hormones are polypeptide or proteinaceous in nature? Choose the correct option.
Hint :-
Conceptual	Easy	Medium		Difficult
IITJEE	AIEEE	BITS		Regional		Board	NCERT
Solution:-	I, II, III and IV. Refer to Ans. No. 83.
						Is Correct
Option 1	I, II, III and IV
Option 2	III, IV, V and VI
Option 3	III, IV, V and VI
Option 4	I, II, III and VI					*

Subject	Unit		Chapter		Day	Maximum Marks:
Zoology			Chemical Coordination and Integration		1	Negative Marks:
Type of Question:-	Single Choice		Multiple			Integer
Source:-
Information:-	Single Choice
Question:- 140	Match the following columns. Column I Column II A. protein hormones 1. Epinephrine B. Steroid hormones 2. Testosterone, progesterone C. Idothyronines hormones 3. Thyroid D. Amino acid derivatives hormones 4. Insulin and glucagon Codes A B C D
Hint :-
Conceptual	Easy	Medium		Difficult
IITJEE	AIEEE	BITS		Regional		Board	NCERT
Solution:-	On the basis of nature, hormones can be divided into four groups (i) peptide, polypeptide , protein hormone (e.g.,) Insulin, glucagon, pituitary hormones, hypothalamic hormones). (ii) Sterols (e.g, Cortisol, testosterone, estradiol and progesterone). (iii) lodothyronine (e.g., Thyroid hormones). (iv) Amino acid derivaties (e.g., Epinephrine).
						Is Correct
Option 1	1 2 3 4
Option 2	4 3 2 1
Option 3	4 2 3 1					*
Option 4	4 2 1 3

Subject	Unit		Chapter		Day	Maximum Marks:
Zoology			Chemical Coordination and Integration		1	Negative Marks:
Type of Question:-	Single Choice		Multiple			Integer
Source:-
Information:-	Single Choice
Question:- 167	Match the following columns and choose the correct option from the codes given below Column I Column II A. Exocrine gland 1. Liver B. Endocrine gland 2. Gastric gland C. Heterocrine gland 3. Thyroid   4. Adrenal gland   5. Ovary   6. Testis Codes
Hint :-
Conceptual	Easy	Medium		Difficult
IITJEE	AIEEE	BITS		Regional		Board	NCERT
Solution:-	Exocrine gland Liver and gastric gland Endocrine gland Thyroid and adrenal gland Heterocrine gland Ovary and testis.
						Is Correct
Option 1	A- 1, 2; B-3, 4; C-5, 6					*
Option 2	A- 1, 2, 3; B-4, 5; C-6
Option 3	A- 1; B-2, 3,4; C-5, 6
Option 4	A- 1; B-2, 3; C-4,5, 6

Subject	Unit		Chapter		Day	Maximum Marks:
Zoology			Chemical Coordination and Integration		1	Negative Marks:
Type of Question:-	Single Choice		Multiple			Integer
Source:-
Information:-	Single Choice
Question:- 192	Tyrosine is the precursor of
Hint :-
Conceptual	Easy	Medium		Difficult
IITJEE	AIEEE	BITS		Regional		Board	NCERT
Solution:-	The conversion of tyrosine to epinephrine involves four steps (i) Ring hydroxylation (ii) Decarboxylation (iii) Side chain hydroxylation (iv) N-methylation Tyrosine Tyrosine hydroxylase (Dihydroxyphenylalanine) Dopa-decarboxylase Dopamine Dopamine--Hydroxylase Norepinephrine PNMT (Phenyl ethanolamine-N-methyl transferase). Epinephrine
						Is Correct
Option 1	Epinephrine
Option 2	Norepinephrine
Option 3	Testosterone
Option 4	Both (a) and (b)					*

Subject	Unit		Chapter		Day	Maximum Marks:
Zoology			Chemical Coordination and Integration		1	Negative Marks:
Type of Question:-	Single Choice		Multiple			Integer
Source:-
Information:-	Single Choice
Question:- 203	Endocrine glands are the glands which
Hint :-
Conceptual	Easy	Medium		Difficult
IITJEE	AIEEE	BITS		Regional		Board	NCERT
Solution:-	Endocrine system is a system of isolated glands that pour their secretion directly into venous blood or lymph for passage to different body organs in order to control their functioning. Metabolism, cell permeability, growth differentiation and stress condition.
						Is Correct
Option 1	Pour their secretions directly into blood					*
Option 2	Pour their secretions indirectly into blood
Option 3	Have ducts
Option 4	All of the above

Subject	Unit		Chapter		Day	Maximum Marks:
Zoology			Chemical Coordination and Integration		1	Negative Marks:
Type of Question:-	Single Choice		Multiple			Integer
Source:-
Information:-	Single Choice
Question:- 205	Reproductive glands are also called
Hint :-
Conceptual	Easy	Medium		Difficult
IITJEE	AIEEE	BITS		Regional		Board	NCERT
Solution:-	Types of glands on the basis of presence or absence of ducts. (i) Exocrine Gland Those which drain out their secretion through duct. Live, gastric glands, etc. (ii) Endocrine Gland Those gland which lack duct and discharge their secretion (hormones) directly into the blood stream. Due to absence of duct they are also called, ductless gland or Holocrine glands, e.g. thyroid, parathyroid, pituitary gland. (iii) Heterocrine Gland Those gland which have dual function due to possession of both exocrine as well as endocrine region. They secrete hormone in association with other substances for their respective function ovary, testes, pancreas.
						Is Correct
Option 1	Exocrine glands
Option 2	Holocrine glands
Option 3	Heterocrine glands					*
Option 4	Enzyme secreting glands

Subject	Unit		Chapter		Day	Maximum Marks:
Zoology			Chemical Coordination and Integration		1	Negative Marks:
Type of Question:-	Single Choice		Multiple			Integer
Source:-
Information:-	Single Choice
Question:- 96	Which of the following are Heterocrine glands. I. Thyroid II. Parathyroid III. Ovary IV. Testis V. Pituitary VI. Pancreas Choose the correct option.
Hint :-
Conceptual	Easy	Medium		Difficult
IITJEE	AIEEE	BITS		Regional		Board	NCERT
Solution:-	Glands which have dual function due to possession of both exocrine as well as endocrine region are called Heterocrine glands. They secrete hormone in association with other substances for their respective function, e.g. ovaries, testes and pancreas.
						Is Correct
Option 1	I, II and III
Option 2	III, IV and VI					*
Option 3	I, V and VI
Option 4	I, IV and V

Subject	Unit		Chapter		Day	Maximum Marks:
Zoology			Chemical Coordination and Integration		1	Negative Marks:
Type of Question:-	Single Choice		Multiple			Integer
Source:-
Information:-	Single Choice
Question:- 100	I. Pancreas II. Testis III. Liver IV. Thyroid gland V. Adrenal gland VI. Pituitary gland Which of the above given glands are endocrine glands?
Hint :-
Conceptual	Easy	Medium		Difficult
IITJEE	AIEEE	BITS		Regional		Board	NCERT
Solution:-	(i) Liver is the exocrine (gland which drains out their secretion through duct). (ii) Pancreas, testis and ovary are the Heterocrine gland. (iii) Thymus, adrenal and pituitary, thyroid are the endocrine gland.
						Is Correct
Option 1	I and II
Option 2	Only III
Option 3	Only VI
Option 4	IV, V and VI					*

Subject	Unit		Chapter		Day	Maximum Marks:
Zoology			Chemical Coordination and Integration		1	Negative Marks:
Type of Question:-	Single Choice		Multiple			Integer
Source:-
Information:-	Single Choice
Question:- 169	Match the following columns. Column I Column II A. Endorine action 1. Hormone act on locally B. Autocrine action 2. Hormone act on distant target C. Paracrine action 3. Hormone act on same cell which produces it. Codes A B C
Hint :-
Conceptual	Easy	Medium		Difficult
IITJEE	AIEEE	BITS		Regional		Board	NCERT
Solution:-	Types of hormone action are (i) Endocrine Action The action in which hormone is distributed in blood and binds to distant target cells. (ii) Paracrine Action The action in hormone acts locally by diffusing from its source to target cells in the neighborhood. e.g., cytokines. (iii) Autocrine Action The action in which hormone acts on the same cell that produced it.
						Is Correct
Option 1	1 2 3
Option 2	3 2 1
Option 3	2 3 1					*
Option 4	2 1 3

Fundamental Theorem Of Arithmetic

Fundamental Theorem of Arithmetic states that every integer greater than 1 is either a prime number or can be expressed in the form of primes. In other words, all the natural numbers can be expressed in the form of the product of its prime factors. To recall, prime factors are the numbers which are divisible by 1 and itself only. For example, the number 35 can be written in the form of its prime factors as:

35 = 7 × 5

Here, 7 and 5 are the prime factors of 35

Similarly, another number 114560 can be represented as the product of its prime factors by using prime factorization method,

114560 = 2⁷ × 5 × 179

So, we have factorized 114560 as the product of the power of its primes.

 

Therefore, every natural number can be expressed in the form of the product of the power of its primes. This statement is known as the Fundamental Theorem of Arithmetic, unique factorization theorem or the unique-prime-factorization theorem.

Proof for Fundamental Theorem of Arithmetic

In number theory, a composite number is expressed in the form of the product of primes and this factorization is unique apart from the order in which the prime factor occurs.

From this theorem we can also see that not only a composite number can be factorized as the product of their primes but also for each composite number the factorization is unique, not taking into consideration order of occurrence of the prime factors.

In simple words, there exists only a single way to represent a natural number by the product of prime factors. This fact can also be stated as:

The prime factorization of any natural number is said to be unique for except the order of their factors.

In general, a composite number “a” can be expressed as,

a = p₁ p₂ p₃ ………… p_n, where p₁, p₂, p₃ ………… p_n are the prime factors of a written in ascending order i.e. p₁≤p₂≤p₃ ………… ≤p_n.

Writing the primes in ascending order makes the factorization unique in nature.

Fundamental Theorem of Arithmetic Examples

Example Question: In a formula racing competition the time taken by two racing cars A and B to complete 1 round of the track is 30 minutes and 45 minutes respectively. After how much time will the cars meet again at the starting point?

Solution:

As the time taken by car B is more compared to that of A to complete one round therefore it can be assumed that A will reach early and both the cars will meet again when A has already reached the starting point. This time can be calculated by finding the L.C.M of the time taken by each.

30 = 2 × 3 × 5

45 = 3 × 3 × 5

The L.C.M is 90.

Thus, both cars will meet at the starting point after 90 minutes.

1.14  the Fundamental theorem of arithmetic :

heorem (Fundamental Theorem of Arithmetic) :
    Every composite number can be expressed (factorised) as a product of primes and this factorisation is unique, apart from the order in which the prime factors occurs.
    The prime factorisation of a natural number is unique except the order of its factors.

Prime Factorisation of Numbers Using Fundamental Theorem of Arithmetic

We know that all composite numbers can be represented as the product of two or more prime numbers. Let us understand this concept by taking the example of 36 and factorising it in different ways.

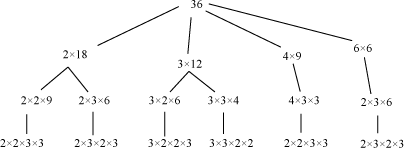
We can see that whichever way we factorise the number 36, it will be broken down as the product of the same prime numbers, which is unique. The only difference is that the ordering of the prime numbers will be different for different ways of factorising the number. In fact, this is true for all numbers. We can check this by taking the example of a larger number, say 21560, which can be uniquely broken down into its prime factors as

2³ × 5 × 7² × 11

Hence, we can say that any composite number can be written in the form of the product of prime numbers, which is unique, except the order in which they occur. By this, we mean that 2 × 3 × 7 × 11 is the same as 7 × 11 × 2 × 3.

This is the fundamental theorem of arithmetic. It can be formally stated as:

Thus, this theorem can be used to write the prime factorisation of any number. Let us try to build on this concept with the help of some examples.

Example 1:

Write the prime factorization of 31250. What are its prime factors? Solution:

31250 = 2 × 15625

= 2 × 5 × 3125

= 2 × 5 × 5 × 625

= 2 × 5 × 5 × 5 × 125

= 2 × 5 × 5 × 5 × 5 × 25

= 2 × 5 × 5 × 5 × 5 × 5 × 5

= 2 × 5⁶

Hence, 2 × 5⁶ is the prime factorisation of 31250. Its prime factors are 2 and 5.

Example 2: If it is given that 13125 = 2^a ×3^b× 5^c× 7^d, then find the value of a +2b +7c + 11d.

Solution:

2^a × 3^b × 5^c × 7^d = 13125

= 3 × 4375

= 3 × 5 × 875

= 3 × 5 × 5 ×175

= 3 × 5 × 5 × 5 × 35

= 3 × 5 × 5 × 5 × 5 × 7

= 3¹ × 54 × 7¹

∴ 2^a × 3^b × 5^c × 7^d = 2⁰ × 3¹ × 5⁴ × 7¹

Comparing exponents of the bases (integers): a = 0, b = 1, c = 4, and d =1

Hence, a +2b +7c +11d = 0 + 2 ×1 + 7 × 4 + 11 × 1

= 0 + 2 + 28 + 11

= 41

Example 3: Show that the expressions given below are composite numbers.

(a) 3 × 5 × 7 × 23 + 2 × 7 × 11 × 13

(b) 29 × 35 + 14

(c) 3⁴ + 6³

Solution:

(a) 3 × 5 × 7 × 23 + 2 × 7 × 11 × 13 = 7( 3 × 5 × 23 + 2 × 11 × 13)

= 7(345 + 286)

= 7 × 631

Since both 7 and 631 are prime numbers, we have expressed the given expression as the product of two prime numbers. We know that according to the fundamental theorem of arithmetic, every composite number can be uniquely written as the product of its prime factors. Thus, the given expression represents a composite number.

(b) 29 × 35 + 14 = 29 × 5 × 7 + 2 × 7

= 7(29 × 5 + 2)

= 7 × 147

= 7 × 3 × 7 × 7

= 3 × 7³

Since both 3 and 7 are prime numbers, we have expressed the given expression as the product of its prime factors. We know that according to the fundamental theorem of arithmetic, every composite number can be uniquely written as the product of its prime factors. Thus, the given expression represents a composite number.

(c) 3⁴ + 6³ = 3⁴ + (2 × 3) ³

= 3⁴ + 2³ × 3³

= 3³(3 + 2³)

= 3³ × 11

Since both 3 and 11 are prime numbers, we have expressed the given expression as the product of its prime factors. It is known that according to the fundamental theorem of arithmetic, every composite number can be uniquely written as the product of its prime factors. Thus, the given expression represents a composite number.

Application Of The Fundamental Theorem Of Arithmetic To Find The HCF And LCM Of Numbers

All composite numbers can be written as the product of two or more prime numbers. For example, 20 can be written as 2² × 5; 54 can be written as 2 × 3³, and so on.

Note that if we do not consider the way in which the prime factors are written, then we can prime factorise every number in only one way. This applies to other numbers as well.

This leads to the fundamental theorem of arithmetic, which states that:

Even though we did not notice it before, whenever we prime factorise a number, we use the fundamental theorem of arithmetic to do so.

For example, the prime factorisation of 980 is represented as

980 = 2 × 490

= 2 × 2 × 245

= 2 × 2 × 5 × 49

= 2 × 2 × 5 × 7 × 7

= 2² × 5¹ × 7²

Hence, 2² × 5¹ × 7² is the prime factorisation of 980; and 2, 5, and 7 are its prime factors.

By applying the fundamental theorem of arithmetic to the prime factorized numbers, we can also find their HCF and LCM.

This is known as the prime factorisation method, which states that:

Let us understand this method with the help of some examples.

Example 1: Find the LCM and the HCF of 432 and 676 using the prime factorization method.

Solution:

We can write these numbers as

432 = 24 × 3³

676 = 2² × 13²

To calculate the HCF

We observe that the only common prime factor is 2 and the smallest power of this prime factor is also 2.

Thus, HCF (432, 676) = 2² = 4

To calculate the LCM

We observe that the prime factors of 432 and 676 are 2, 3, and 13. The greatest powers of these factors are 4, 3, and 2 respectively.

LCM is the product of the greatest power of each prime factor.

Thus, LCM (432, 676) = 2⁴ × 3³ × 13² = 73008

Example 2: Find the HCF and the LCM of 28, 42, and 64 using the prime factorization method.

Solution:

We can write these numbers as

28 = 2² × 7¹

42 = 2 × 3¹ × 7¹

64 = 2⁶

HCF is the product of the smallest power of each common prime factor. Here, the only common prime factor is 2 and its power is 1.

Thus, HCF (28, 42, 64) = 2¹ = 2

LCM is the product of the greatest power of each prime factor. Thus, LCM (28, 42, 64) = 2⁶ × 3¹ × 7¹ = 1344

Example 3: Find the HCF and the LCM of 1080 and 900 using the prime factorization and show that HCF × LCM = Product of two numbers.

Solution:

1080 = 2³ × 3³ × 5

900 = 2² × 3² × 5²

Hence, HCF (1080, 900) = 2² × 3² × 5 = 180

LCM (1080, 900) = 2³ × 3³ × 5² = 5400

HCF × LCM = 180 × 5400 = 972000

Product of numbers = 1080 × 900 = 972000

Hence, HCF × LCM = Product of two numbers

Example 4: The HCF of 273 and another number is 7, while their LCM is 3003. Find the other number.

Solution:

Let the first number (a) be 273 and the second number be b.

It is given that HCF (a, b) = 7 and LCM (a, b) = 3003.

We know that HCF LCM = Product of two numbers.

⇒ HCF (a, b) × LCM (a, b) = a × b

⇒ 7 × 3003 = 273 × b

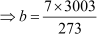
⇒ b = 77

Hence, the other number is 77.

Example 5: Anurag takes 6 minutes to complete one round of jogging around the circular track of a park, while Twinkle takes 8 minutes to do the same. If both of them start jogging at the same time from the same point, then how much time will they take before they meet at the point from which they started?

Solution:

Since Anurag and Twinkle take 6 minutes and 8 minutes respectively to complete one round of the circular track, the time after which they will meet at the starting point will be the lowest multiple of 6 and 8, i.e., their LCM.

6 = 2 × 3

8 = 2³

∴ LCM (6, 8) = 2³ × 3 = 24

Thus, they will meet at the starting point after 24 minutes.

Example 6: There are 120 students in a class. When the students were arranged according to their roll numbers, it was observed that every second student got distinction in Mathematics, every third student got distinction in Science, and every fifth student got distinction in English. How many students got distinction in all three subjects?

Solution:

As every second, third, and fifth student got distinction in Math, Science, and English respectively, the roll numbers of the students who got distinction in all three subjects will be equal to the multiples of the LCM of 2, 3, and 5.

LCM (2, 3, 5) = 2 × 3 × 5 = 30

Thus, every 30^th student got distinction in all three subjects.

Thus, a total of 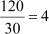students got distinction in all three subjects.

Properties Of Prime Numbers

Consider the number 8ⁿ, where n is a natural number.

Is there any value of n for which 8ⁿ ends with zero?

It is difficult to answer this question directly. However, we can answer this question by making use of the fundamental theorem of arithmetic. It states that

This means that if we are given a composite number, then that number can be written as a product of prime numbers in only one way (except for the order of prime numbers).

For example: the composite number 255 can be written as the product of primes as follows. 255 = 3 × 5 × 17

Also, 255 can be written as 3 × 17 × 5 or 5 × 3 × 17 or 5 × 17 × 3 or 17 × 3 × 5 or 17 × 5 × 3.

Thus, we can see that 255 can be expressed as a product of unique prime numbers 3, 5, and 17 but the order of representation may differ.

Now, by making use of the above theorem, we can answer the question which we were discussing in the beginning. Let us see how.

Suppose the number 8n ends with zero for some value of n. Since the number ends with zero, it should be divisible by 10. Now, 10 = 2 × 5

Thus, this number should be divisible by 2 and 5 also.

Therefore, the prime factorization of 8n should contain both the prime numbers 2 and 5. We have, 8ⁿ = (2³)ⁿ = 2³ⁿ

⇒ The only prime in the factorization of 8ⁿ is 2.

Thus, by fundamental theorem of arithmetic, there is no other prime in the factorization of 8ⁿ.

Hence, there is no natural number n for which 8n ends with the digit zero. In this way, we can make use of the above theorem.

Let us now look at some more examples to understand this concept better.

Example 1: Prove that the number 9ⁿ, where n is a natural number, cannot end with a zero.

Solution:

Suppose the number 9ⁿ ends with a zero for some value of n.

Since the number ends with zero, it should be divisible by 10.

Now, 10 = 2 × 5

Thus, this number should be divisible by 2 and 5 also.

Therefore, the prime factorization of 9ⁿ should contain both the prime numbers 2 and 5.

We have, 9ⁿ = (32)ⁿ = 3²ⁿ

⇒ The only prime in the factorization of 9ⁿ is 3.

Thus, by fundamental theorem of arithmetic, there is no other prime in the factorization of 9ⁿ.

Hence, there is no natural number n for which 9ⁿ ends with the digit zero.

Example 2: Check whether the numbers 49ⁿ, where n is a natural number, can end with a zero.

Solution:

Suppose the number 49n ends with a zero for some value of n.

Since the number ends with zero, it should be divisible by 10.

Now, 10 = 2 × 5

Thus, this number should be divisible by 2 and 5 also.

Therefore, the prime factorization of 49n should contain both the prime numbers 2 and 5. We have, 49ⁿ = (7²)ⁿ = 7²ⁿ

⇒ The only prime in the factorization of 49ⁿ is 7.

Thus, by fundamental theorem of arithmetic, there is no other prime in the factorization of 49ⁿ.

Thus, there is no natural number n for which 49ⁿ ends with the digit zero.