Chapter 6: Triangles

Difference Between Similarity and Congruence

Similar figures and congruent figures may appear to be closely related concepts, but there is an important difference between them.

Congruency of line segments:

“Two line segments are congruent to each other if their lengths are equal”.

Consider the following line segments.

Here, the line segments AB and PQ will be congruent to each other, if they are of equal length.

Conversely, we can say that, “Two line segments are of equal length if they are congruent to each other”.

i.e. if 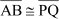, then AB = PQ.

Congruency of angles:

“Two angles are said to be congruent to each other if they have the same measure”.

The angles shown in the following figures are congruent to each other as both the angles are of the same measure 45°.

Thus, we can write ∠BAC ≅ ∠QPR.

Its converse is also true.

“If two angles are congruent to each other, then their measures are also equal”.

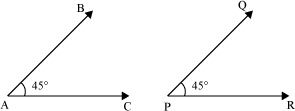
There is one special thing about congruent figures that their corresponding parts are always equal.

For example, if two triangles are congruent then their corresponding sides will be equal. Also, their corresponding angles will be equal.

Look at the following triangles.

Here, ∆ABC ∆DEF under the correspondence ∆ABC ↔ ∆DEF. This correspondence rule represents that in given triangles, AB ↔ DE (AB corresponds to DE), BC ↔ EF, CA ↔ FD, ∠A

— ∠D, ∠B ↔ ∠E, ∠C ↔ ∠F. These are corresponding parts of congruent triangles (CPCT), ∆ABC and∆DEF.

Since ∆ABC and ∆DEF are congruent, their corresponding parts are equal. Therefore, AB = DE, BC = EF, CA = FD

And, ∠A = ∠D, ∠B = ∠E, ∠C = ∠F

Similarly, we can apply the method of CPCT on other congruent triangles also. Let us now try and apply what we have just learnt in some examples.

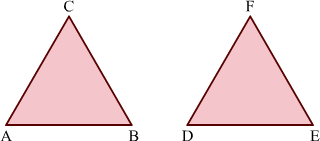
Example 1: Find which of the pairs of line segments are congruent.

(i)

(ii)

Solution:

(i)    Lengths of the two line segments are not same. Therefore, they are not congruent.

(ii)    Each of the line segments is of length 3.1 cm, i.e. they are equal. Therefore, they are congruent.
 

Example 2: If 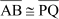and 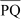= 9 cm, then find the length of 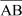. Solution:

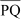Since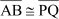 , i.e. line segment AB is congruent to line segment PQ,

therefore, and are of equal length.

∴ = 9 cm

Example 3: If ∠ABC ∠PQR and ∠PQR = 75o, then find the measure of ∠ABC. Solution:

If two angles are congruent, then their measures are equal.

Since ∠ABC ≅ ∠PQR,

∴ ∠ABC = ∠PQR T

herefore, ∠ABC = 75^o

Example 4: Which of the following pairs of angles are congruent?

(i)

(ii)

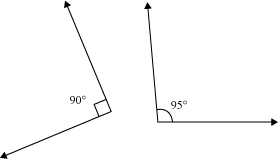
Solution:

(i)    The measure of both the angles is the same. Therefore, they are congruent.

(ii)    The measures of the two angles are different. Therefore, they are not congruent.

Example 5: Identify the pairs of similar and congruent figures from the following. 

(i)

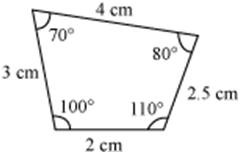
(ii)

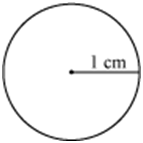
(iii)    

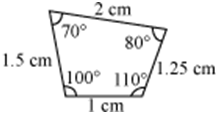
(iv)    

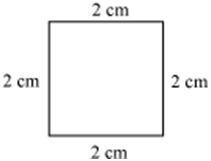
(v)    

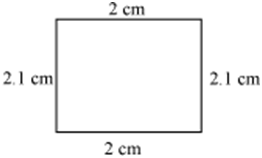
(vi)    

(vii)    

(viii)    

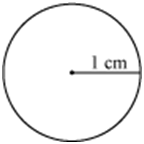
Solution:

Figures (i) and (iii) are similar because their corresponding angles are equal and their corresponding sides are in the same ratio. However, these figures are not congruent as they are of different sizes.

Figures (ii) and (viii) are congruent as they are of the same shape and size (circles with radius 1 cm each).

Example 6:

Are the following figures similar or congruent?

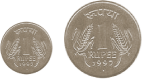
Solution:

The two given figures show two one-rupee coins. As both the figures represent the same coin in two different sizes, they are similar to each other. However, the pictures are not congruent because of their different sizes.

Example 7: In the following figure, ΔPQR and ΔSTU are congruent.

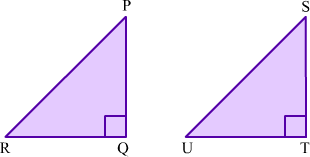
If PQ = 8 cm, QR = 6 cm then find the perimeter of ΔSTU.

Solution:

In ΔPQR, we have

PQ = 8 cm, QR = 6 cm and ∠Q = 90°

Applying Pythagoras theorem in ΔPQR, we obtain

RP² = PQ² + QR²

⇒ RP² = 8² + 6²

⇒ RP² = 64 + 36

⇒ RP² = 100

⇒ RP = 10 cm

Since ΔPQR and ΔSTU are congruent, their corresponding parts will be equal. Therefore,

PQ = 8 cm = ST (CPCT)

QR = 6 cm = TU and (CPCT) RP = 10 cm = US (CPCT)

∴ Perimeter of ΔSTU = ST + TU + US = 8 cm + 6 cm + 10 cm = 24 cm

Basic Proportionality Theorem and Its Converse

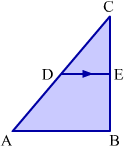
Consider the following figure.

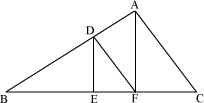
In the above figure, DE is parallel to AF and DF is parallel to AC. Can we say that point E divides BF in the same ratio in which point F divides BC?

For this, we have to prove that .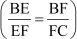

To prove it, we should have the knowledge of basic proportionality theorem (Thales theorem).

Now, let us solve the problem discussed in the beginning with the help of BPT. In ABF, we know that AF is parallel to DE.

Thus, using BPT,

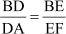… (1)

Similarly in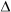 ABC, DF is parallel to AC. Thus, using BPT,

… (2)

From equations (1) and (2), we obtain

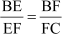
Thus, we can say that point E divides BF in the same ratio in which point F divides BC. The converse of BPT is also true, which can be stated as follows.

“If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side”.

Corollary of BPT:

If a line is drawn parallel to a side of a triangle, then the sides of the new triangle formed are proportional to the sides of the given triangle.

I.e, In the given figure, if DE || AB, then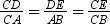

Applications of Basic Proportionality Theorem:

There are two very important properties based on BPT which are as follows:

1. Property of intercepts made by three parallel lines on a transversal.
2. Property of angle bisector of a triangle.

Let us discuss these properties in detail along with their proofs.

Property 1: Intercept Theorem

The lengths of the intercepts made by three parallel lines on one transversal are in the same ratio as the lengths of the corresponding intercepts made by the same lines on any other transversal.

Let us prove this property.

Given: line l || line m || line n

Transversal x intersects these lines at points P, Q and R while transversal y intersects these lines at points S, T and U.

To prove: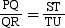

Construction: Draw a line segment PU intersecting line m at point M.

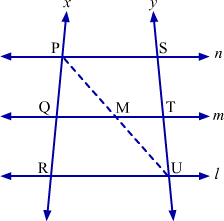
Proof:

In ΔPRU, we have QM || RU

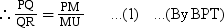
Similarly, in ΔUSP, we have TM || SP

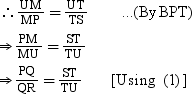
Hence proved.

Property 2: Angle Bisector Theorem

In a triangle, the angle bisector divides the side opposite to the angle in the ratio same as the ratio of remaining sides.

Let us prove this property.

Given: In ΔPQR, ray RT bisects ∠PRQ.

To prove: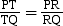

Construction: Draw a ray from Q parallel to ray RT such that it intersects extended PR at S.

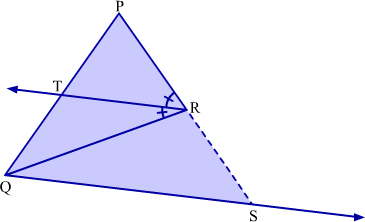
Proof:

We have,

RT || QS and PS is transversal

∴ ∠PRT = ∠RSQ ...(1) (Corresponding angles)

Considering other transversal RQ, we obtain

∠TRQ = ∠RQS ...(2) (Alternate angles) But ∠PRT = ∠TRQ (RT bisects ∠PRQ)

∴ ∠RSQ = ∠RQS [Using (1) and (2)]

Thus, in ΔRQS,

RS = RQ ...(3) (Side opposite to equal angles are equal) Now, in ΔPQS, we have

RT || QS

Hence proved.

Property 3: Converse of Angle Bisector Theorem

If a straight line through one vertex of a triangle divides the opposite side in the ratio of the other two sides, then the line bisects the angle at the vertex.

Let us prove this property.

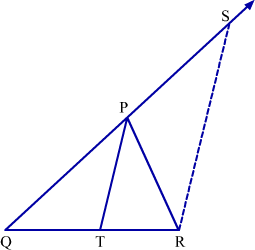
Given: In ΔPQR, line PT divides the opposite side BC internally such that.

Hence proved.

These properties are very useful sometimes.

Let us now solve some examples based on BPT, its converse and properties related to BPT.

Example 1: In triangle ABC, D and E are points on the sides AB and AC, such that AB =11.2 cm, AD = 2.8 cm, AC = 14.4 cm, and AE = 3.6 cm. Show that DE is parallel to BC.

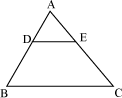
Solution:

It is given that,

AB = 11.2 cm, AD = 2.8 cm, AC =14.4 cm, and AE = 3.6 cm

Therefore, BD = AB – AD = 11.2 – 2.8 = 8.4 cm

And,

EC = AC –AE =14.4 – 3.6 = 10.8 cm

Now,

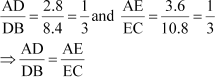
Thus, DE divides sides AB and AC of triangle ABC in the same ratio. Therefore, by the converse of BPT, we obtain that DE is parallel to BC.

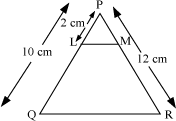
Example 2: In the figure shown below, find the length of PM, if it is given that LM || QR. The corresponding measures are shown in the figure.

Solution:

Here, LM || QR

Then, using basic proportionality theorem, we obtain

Let PM = x cm

Then, MR = 12 – x cm And, PL = 2 cm

LQ = 10 cm – 2 cm = 8 cm

On putting these values in equation (i), we obtain

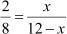
2(12 – x) = 8x

24 – 2x = 8x

24 = 8x + 2x

24 = 10x

x = 2.4 cm

Thus, PM = 2.4 cm

Example 3: If ABCD is a trapezium with AD || BC, then prove that , where O is the point of intersection of diagonals AC and BD.

Solution:

A trapezium has been shown in the following figure.

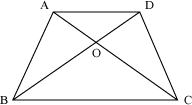
A line LM is drawn parallel to AD and BC and passing through O.

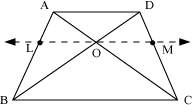
Here, LO || BC.

Using BPT in ΔABC,

Similarly, using BPT in ΔABD as LO || AD, we obtain

From equations (i) and (ii), we obtain

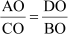
Hence, proved

Example 4: In ΔPQR, LM || QR and L is the mid-point of side PQ. Show that PM = MR.

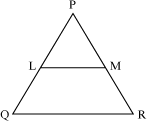
Solution:

Here, LM || QR

Using basic proportionality theorem (BPT),

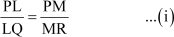
Now, L is the mid-point of PQ.

∴ PL = LQ

Using this in equation (i), we obtain

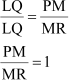
∴ PM = MR

Hence, proved

Example 5: In trapezium ABCD, AB || EF || DC. Find the length of BF and FC.

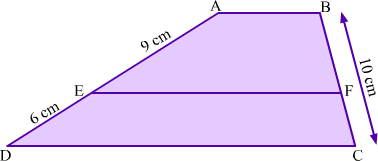
Solution:

In trapezium ABCD, AB || EF || DC.

Here, AD and BC are transversals to parallel segments AB, EF and DC.

Intercepts made by AD are AE and ED while intercepts made by BC are BF and FC. Using property of intercepts made by three parallel lines on a transversal, we obtain

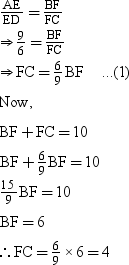
Thus, BF = 6 cm and FC = 4 cm.

Example 6: In ΔABC, BD bisects ∠ABC. Find the length of AD.

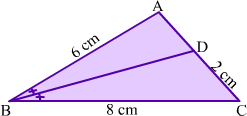
Solution:

In ΔABC, BD bisects ∠ABC

Thus, by using the property of angle bisector of a triangle, we obtain

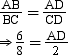
⇒ AD = 1.5

Hence, the length of AD is 1.5 cm.

Example 7.

In the given figure, DE || AB. If perimeter of Δ ABC : perimeter of ΔCDE = 4:5 and DE = 1.2 cm, then find the length of AB.

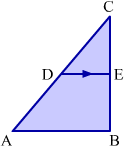
Answer:

It is given that, perimeter of ΔABC : perimeter of ΔCDE = 4:5 and DE = 1.2. InΔ ABC, DE || AB.

By applying the corollary of basic proportionality theorem, we get

AAA Criterion Of Similarity Of Triangles

We have various criteria to prove two triangles similar. AAA criterion is one of these.

We can check the similarity of any two triangles using AAA criterion of similarity if any two angles of each triangle are given so, AAA criterion is same as AA criterion.

AA criterion "If two triangles are equiangular, then their corresponding sides are proportional." can be proved as below.

Given: ΔABC and ΔPQR where ∠A = ∠P, ∠B = ∠Q and ∠C = ∠R.

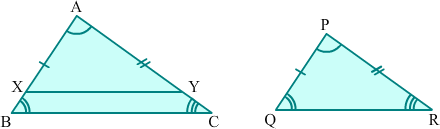
To prove:

Construction: Mark X and Y on AB and AC respectively such that AX = PQ and AY = PR.

Proof:

In ΔAXY and ΔPQR,

AX = PQ [By construction]

∠A = ∠P [Given]

AY = PR [By construction]

So, by SAS postulate, ΔAXY ≡ ΔPQR.

[Note: The symbol '≡' stands for congruency]

⇒XY = QR and ∠X = ∠Q [CPCT]

Now, ∠X = ∠B [∠X = ∠Q = ∠B]

∴XY||BC [∠X and ∠B are corresponding angles]

Hence, AA criterion is proved.

Now, look at the following triangles.

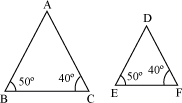
Here, ∠B = ∠E = 50°

and ∠C = ∠ F = 40°

Then, using AAA similarity criterion, ΔABC is similar to ΔDEF.

In symbolic form, we can write ΔABC ∼ ΔDEF. In symbolic form, the order of vertices is very important. For the above triangles, we cannot write ΔABC ∼ ΔEFD because ∠B = ∠E and ∠C = ∠F

Let us look at one more application of the AAA similarity criterion in the video in order to get a better understanding of this concept.

Converse of AAA criterion is also true which states that:

If two triangles are similar then their corresponding angles are equal.

For example, if ΔABC ∼ ΔDEF then ∠A = ∠D, ∠B = ∠E and ∠C = ∠ F.

Note: In some state boards, the symbol "|||"is used for similarity.

I.e., ΔABC ∼ ΔDEF may also be written as ΔABC ||| ΔDEF.

Let us now look at some more problems based on AAA similarity criterion.

Example 1: In the following figure, if DE || BC, then prove the following.

(a) ΔABC ∠ ΔADE

(b) ΔDFE ∠ ΔCFB

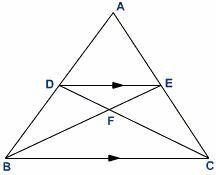
Solution:

(a) In ΔABC and ΔADE,

∠BAC = ∠DAE (Common to both)

∠ADE = ∠ABC (Since DE is parallel to BC, ∠ADE and ∠ABC are corresponding angles) By AAA similarity criterion,

ΔABC ∼ ΔADE

(b) In ΔDFE and ΔBFC,

∠DFE = ∠BFC (Vertically opposite angles)

∠EDF = ∠BCF (Alternate angles) By AAA similarity criterion,

ΔDFE ∼ ΔCFB

Example 2: In the given figure, if WY || ZX, then prove that ΔOWY ∠ ΔOXZ.

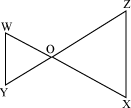
Solution:

Here, WY || ZX

Now, in ΔOWY and ΔOZX,

∠WOY = ∠ZOX (Vertically opposite angles)

∠OWY = ∠OXZ (Alternate angles)

∠OYW = ∠OZX (Alternate angles)

By AAA similarity criterion of triangles, ΔOWY ∼ ΔOXZ

SSS Criterion of Similarity of Triangles

Now that we have understood the concept of AAA similarity criterion, we will try and understand another similarity criterion which is the SSS similarity criterion. It involves the ratio of the corresponding sides of the two triangles.

Converse of SSS criterion is also true which states that:

If two triangles are similar then their corresponding sides are proportional.

For example, if ΔABC ∼ ΔPQR then .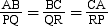

Let us solve some problems to understand this concept better.

Example 1: If PQR is an isosceles triangle with PQ = PR and A is the mid-point of side QR, then prove that ΔPAQ is similar to ΔPAR.

Solution:

It is given that ΔPQR is an isosceles triangle and PQ = PR.

In triangles PAQ and PAR, PQ = PR

Also, A is the mid-point of QR, therefore

QA = AR

And, PA = PA (Common to both triangles)

Therefore, we can say that

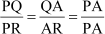
∴ Using SSS similarity criterion, we obtain ΔPAQ ∼ ΔPAR

Example 2: In the following figure, E and D are the mid-points of the sides BC and AC respectively. Prove that ΔABC∠ΔDEC.

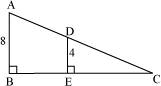
Solution:

It is given that E is the mid-point of BC.

∴ BE = EC

Now, BC = BE + EC

⇒ BC = 2EC

⇒

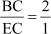Similarly, D is the mid-point of AC, therefore

AC = 2DC

⇒

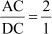
Also, from the figure,

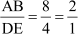
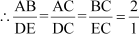
By SSS criterion of similarity of triangles,

ΔABC ∼ ΔDEC

Example 3: In the following figure, the lines XC and YC of same length are drawn such that C is the mid-point of AB. If AX = BY, then find the measure of the following angles.

[1] ∠BYC (c) ∠CAX

[2] ∠CBY (d) ∠ACX

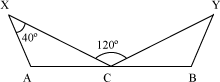
Solution:

In the triangles CAX and CBY,

CX = CY (Given)

CA = CB (C is the mid-point of AB)

AX = BY (Given)

Therefore, by SSS similarity criterion, ΔCAX ∼ ΔCBY

We know that the corresponding angles of similar triangles are equal.

∴ ∠AXC = ∠BYC = 40°

⇒ ∠BYC = 40°

Also, ∠ACX = ∠BCY

Let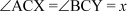

Therefore, x + x + 120° = 180° (∠ACX, ∠BCY, and ∠XCY form a linear pair)

⇒ 2x = 180° − 120° = 60°

⇒ x = 30°

∴ ∠ACX = ∠BCY = 30°

Now, by angle sum property in ΔACX, we obtain

30° + ∠CAX + 40° = 180°

⇒ ∠CAX = 180° − 70° = 110°

∴ ∠CBY = ∠CAX = 110°

Thus, we obtain

1. ∠BYC = 40°

2. ∠CBY = 110°

3. ∠CAX = 110°

4. ∠ACX = 30°

Example 4: ABCD is a square and PQS is an isosceles triangle with PQ = PS and R is the mid-point of QS. If ΔABD ∠ ΔRPQ, then prove that ΔCBD ∠ ΔRPS.

Solution:

ABCD is a square and PQS is an isosceles triangle.

Therefore, AB = BC = CD = DA

And, PQ = PS

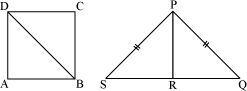
It is also given that ΔABD ∼ ΔQRP.

In

AB = CB (Sides of a square)

BD = BD (Common side)

DA = DC (Sides of a square)

By SSS similarity criterion,

ΔABD ∼ ΔCBD … (2)

Now, in ΔRPQ and ΔRPS,

RP = RP (Common side)

PQ = PS (Equal sides of an isosceles triangle)

QR = SR (R is the mid-point of QS)

Therefore, ΔRPQ ∼ ΔRPS … (3)

However, ΔABD ∼ ΔRPQ

Therefore, from (2) and (3), we obtain

ΔCBD ∼ ΔRPS

SAS Criterion Of Similarity Of Triangles

Look at the following figures.

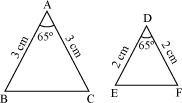
Is there any similarity between them?

We can see that in both the triangles, the lengths of two sides are given and also the measure of the included angle is given. Now, let us compare the sides of the triangles and observe the result we obtain.

On taking the ratio of the sides, we obtain

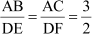
Therefore, we observe that the sides of the triangles are in the same ratio i.e., we can say that the sides of the triangles are proportional.

Using the above fact, can we say that the given triangles are similar?

To know the answer, let us first know about a similarity criterion known as SAS similarity criterion.

SAS similarity criterion can be stated as follows.

“If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar”.

Using this criterion, we can check the similarity of any two triangles, if the two sides and the included angle between them are given.

In the above example, ∠A = ∠D = 65° and the sides including these angles are in the same

proportion i.e., . 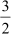Thus, we can say that ΔABC is similar to ΔDEF.

In symbolic form, we can write ΔABC ∼ ΔDEF. For writing the symbolic form, the order of the vertices is very important.

For example, consider the following figure.

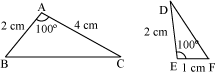
Here, ΔABC and ΔDEF are similar triangles as two sides of both the triangles are proportional and the angles included between them are also equal.

Therefore, we can write ΔABC ∼ ΔEFD.

Let us now look at some more examples to understand this concept better.

Example1: If PQRS is a parallelogram, then prove that ΔSOR is similar to ΔPOQ.

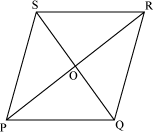
Solution:

Consider ΔSOR and ΔPOQ.

Since PQRS is a parallelogram, the diagonals bisect each other.

∴ SO = OQ and PO = OR

and ∠POQ = ∠SOR (Vertically opposite angles)

By SAS similarity criterion, we obtain

ΔSOR ∼ ΔQOP

Example2: ΔABC is an isosceles triangle with AB and AC as the equal sides. The points D and E divide the side BC into three equal parts as shown in the figure. Prove that ΔABD ∠ ΔACE.

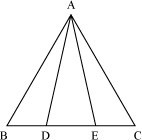
Solution:

Since ABC is an isosceles triangle,

AB = AC

∠ABC = ∠ACB (Angles opposite to equal sides are equal in an isosceles triangle)

It is given that the points D and E divide the side BC in three equal parts. Therefore,

BD = DE = EC

In ΔABD and ΔAEC,

AB = AC

BD = EC

∠ABD = ∠ACE

By SAS similarity criterion,

ΔABD ∼ ΔACE

AREAS OF SIMILAR TRIANGLES

We know what similar triangles are. Now, let us learn about an interesting theorem related to areas of similar triangles.

The theorem states that:

The ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.

Let us prove this theorem.

Given: ΔABC ∼ ΔXYZ

To prove: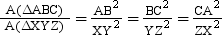

Construction: Draw segment AD perpendicular to BC and segment XP perpendicular to YZ.

Proof:

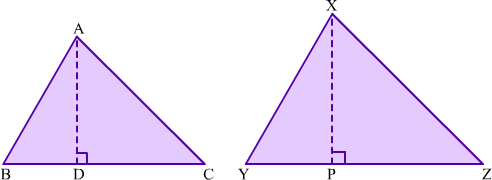
From the figure, we have

Thus, the ratio of areas of similar triangles is equal to the ratio of squares of their corresponding sides.

Let A₁ and A₂ be the areas of similar triangles and s₁ and s₂ be their corresponding sides. Then

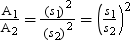
Now, let us learn to apply this formula with the help of an example.

Consider a trapezium PQRS in which SR = 3 PQ. The diagonals PR and QS intersect each other at O.

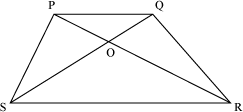
If the area of ΔPOQ is 9 square cm, then what will be the area of ΔSOR? Relation between areas, heights, medians and perimeters of similar triangles:

Let A1 and A2 be the areas of two similar triangles such that s1 and s2 are their corresponding sides, h1 and h2 are their corresponding heights, m1 and m2 are their corresponding medians and P1 and P2 are their respective perimeters.

Then,

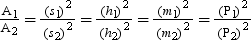
Let us go through some examples based on the areas of similar triangles.

Example 1: The ratio of areas of two similar triangles is 16:25. Find the ratio of their corresponding sides.

Solution:

We know that,

Ratio of areas of similar triangles = (Ratio of corresponding sides)2

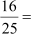⇒ (Ratio of corresponding sides)²

Ratio of corresponding sides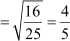

= 4:5

Example 2: The areas of two similar triangles are 25 cm² and 100 cm². If one side of the first triangle is 4 cm, then find the corresponding side of the other triangle.

Solution:

Let ABC and DEF be two triangles whose areas are 25 cm² and 100 cm² respectively. Let AB = 4 cm

Then, we have to find DE.

Since the two triangles ABC and DEF are similar,

(DE)² = 64

DE = 8 cm

Thus, the corresponding side of the other triangle is 8 cm.

Example 3: In a triangle ABC, X, Y, and Z are the mid-points of the sides BC, AC, and AB respectively. Find the ratios of the areas of ΔABC and ΔXYZ.

Solution:

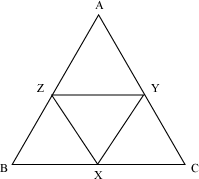
Here, X, Y, and Z are the mid-points of sides BC, AC, and AB respectively.

We know that the line joining the mid-points of two sides is parallel to the third side and its length is half of the third side.

∴ XY || AB and XY =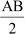

YZ || BC and YZ =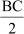

Again, XZ || AC and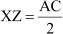

As, XY || AB, YZ || BC, and XZ || AC,

∴ Quadrilaterals AYXZ, BXYZ, and CXZY are parallelograms.

∴ ∠BAC = ∠ZXY, ∠ABC = ∠ZYX, and ∠ACB = ∠XZY

Using AAA similarity criterion, we obtain

ΔABC ∼ ΔXYZ

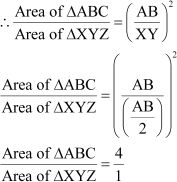
Area of ΔABC: Area of ΔXYZ = 4:1

Example 4: In the given figure, AB and CD are perpendiculars to the line segment BC. Also, AB = 5 cm, CD = 8 cm, and area of ΔAOB is 175 cm². Find the area of ΔCOD.

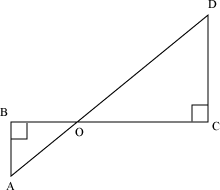
Solution:

Here, ΔAOB and ΔDOC are similar triangles because

∠ABO = ∠DCO (Each 90°)

∠AOB = ∠COD (Vertically opposite angles)

Therefore, by AAA similarity criterion, ΔAOB ∼ ΔDOC

Thus, the area of ΔCOD is 448 cm².

Pythagoras Theorem and Its Applications

Look at the following right triangle ABC.

We have the following relationship between the sides of a right-angled triangle ABC. (AC)² = (AB)² + (BC)²

This relation between the sides of a right-angled triangle is known as Pythagoras Theorem.

This theorem has several other proofs also. Let us discuss two of them here.

Proof by American President:

The 20th president of United States, James Garfield proved this theorem taking two right angled triangles having sides as a, b and c and an other right angled triangle with side c.

The proof given by him is as follows:

All three triangles are combined as shown in the following figure.

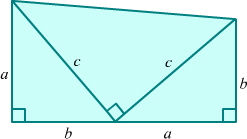
Thus, we got a trapezium.

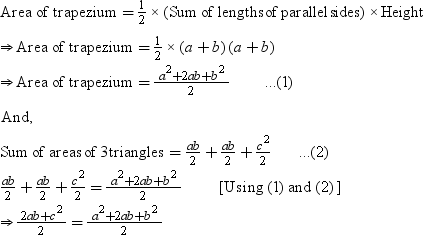
⇒ 2ab + c² = a² + 2ab + b²

⇒ c² = a² + b²

This theorem of right angled triangles was also known to Indian, Chinese, Greek and Babylonian mathematician long before Pythagoras lived. Thus, it was proved by the mathematicians of that time differently.

Proof by Indian Mathematician:

Bhaskaracharya, the great Indian mathematician of 2^nd century AD, used the below given diagrams to prove this theorem.

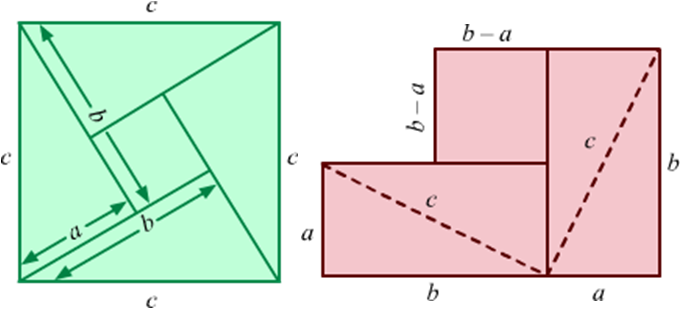
Area of small square = (b – a)² = b² – 2ab + a²

Area of big square = Area of 4 triangles + Area of small square

⇒ c² = 2ab + (b² – 2ab + a²)

⇒ c² = 2ab + b² – 2ab + a²

⇒ c² = b² + a²

Bhaskaracharya proved this theorem by using property of similarity also, but we will not discuss it here.

Note: Conventionally in ΔABC, we consider the lengths of sides opposite to vertices A, B and C as a, b and c respectively.

In real life, we come across many situations where a right angle is formed. Let us consider such a situation.

A 10m long ladder is placed on a wall such that the ladder touches the wall at 8m above the ground. This situation can be shown geometrically as follows.

In the above figure, AB is the wall of height 8 m and AC is the ladder of length 10 m. We know that a wall is perpendicular to the floor, i.e. AB is perpendicular to BC. Thus, ∠ABC is a right angle.

Now, can we calculate the distance of the foot of the ladder from the base of the wall?

We can calculate the distance of the foot of the ladder from the base of the wall by using Pythagoras theorem.

In this way, we can use Pythagoras theorem in many situations where right-angled triangle is formed.

Is the converse of Pythagoras theorem also true? Yes, the converse of Pythagoras theorem is also true. Its converse can be stated as follows:

“In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite to the first side is a right angle”.

But how will we prove it?

Thus, in a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite to the first side is a right angle.

Using the converse, we can check whether the given triangle is a right triangle or not.

Let ABC be a triangle with sides AB = 2.5 cm, BC = 6 cm and CA = 6.5 cm. Can we say that the triangle ABC is a right-angled triangle?

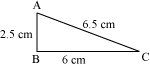
Here, (AB)² = (2.5)² = 6.25

(BC)² = 6² = 36

And, (CA)² = (6.5)² = 42.25

Therefore, we obtain

(AB)² + (BC)² = 6.25 + 36 = 42.25 = (CA)²

Thus, using the converse of Pythagoras theorem, we can say that the angle opposite to the side CA, i.e. ∠B, is a right angle.

Pythagorean triplet: Any three natural numbers a, b, c form a Pythagorean triplet if it satisfies a² = b² + c² irrespective of order.

General form to find the Pythagorean Triplets:

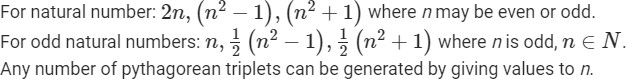
For example, the number 39, 80, and 89 forms a Pythagorean triplet.

39² = 1521

80² = 6400

89² = 7921

Now, 1521 + 6400 = 7921

∴39² + 80² = 89²

Here, the square of a number is equal to the sum of the squares of the other two numbers. Therefore, we can say that 39, 80, and 89 forms a Pythagorean triplet.

Applications of Pythagoras theorem:

Though Pythagoras theorem holds true for only right angled triangle, it can be applied to obtuse and acute angled triangles as well. The obtained results are discussed below:

{1] In acute angled ΔPQR , if PS ∠ QR, QSR is a line and ∠Q < 90° then

PR² = PQ² + QR² – 2QR . QS

Proof: Observe the acute angled triangle ΔPQR.

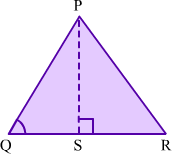
Here, PS ⊥ QR, QSR is a line and ∠Q < 90°.

In ΔPSQ, we have

PQ² = PS² + QS² ...(1) (By Pythagoras theorem)

In ΔPSR, we have

PR2 = PS² + SR² (By Pythagoras theorem)

⇒ PR² = PS² + (QR – QS)²

⇒ PR² = PS² + QR² + QS² – 2QR . QS

⇒ PR² = (PS² + QS²) + QR² – 2QR . QS

⇒ PR² = PQ² + QR² – 2QR . QS [Using (1)]

Hence proved.

(2)    In obtuse angled ΔPQR , if PS ∠ QR, SQR is a line and ∠Q > 90° then

PR² = PQ² + QR² + 2QR . QS

Proof:

Observe the acute angled triangle ΔPQR.

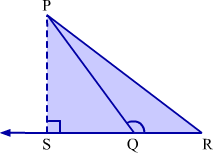
Here, PS ⊥ QR, SQR is a line and ∠Q > 90°.

In ΔPSQ, we have

PQ² = PS² + QS² ...(1)

(By Pythagoras theorem) In

ΔPSR, we have

PR² = PS² + SR² (By Pythagoras theorem)

⇒ PR² = PS² + (QR + QS)²

⇒ PR² = PS² + QR² + QS² + 2QR . QS

⇒ PR² = (PS² + QS2) + QR² + 2QR . QS

⇒ PR² = PQ² + QR² + 2QR . QS [Using (1)]

Hence proved.

Now, let us discuss some more examples based on Pythagoras theorem and its converse.

Example 1: ΔPQR is an isosceles triangle, right angled at Q. Prove that PR² = 2PQ².

Solution:

Here, PQR is an isosceles triangle, right angled at Q. Therefore,

PQ = QR … (1)

Now, using Pythagoras theorem, we obtain

(PR⁾² = (PQ)² + (QR)²

Using equation (1), we obtain

(PR)² = (PQ)² + (PQ)²

(PR)² = 2(PQ)²

Example 2: Two poles are of length 5m and 11m. The distance between the feet of the poles is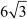 m. Find the distance between the tops of the poles.

Solution:

The figure for the given situation can be drawn as follows.

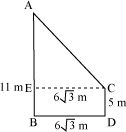
In the above figure, the poles are denoted by AB and CD, where AB = 11 m and CD = 5 m. The distance between the feet of the poles, i.e. BD, is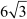 m.

Let us draw a perpendicular CE from C on AB

. AC is the distance between the top of the poles.

Here, BD = CE = 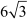m

And AE = AB− BE

= AB − CD [since BE = CD]

= (11 − 5) m

= 6 m

Using Pythagoras theorem in ΔACE, we obtain

(AC)² = (AE)² + (EC)²

(AC)2 = (6)2 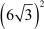m² + m²

= (36 + 108) m²

= 144 m²

⇒ AC =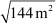

⇒ AC = 12 m

Thus, the distance between the tops of the poles is 12 m.

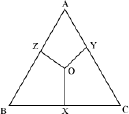
Example 3: O is any point in the interior of ΔABC and OX, OY, and OZ are the perpendiculars drawn from O to BC, CA, and AB respectively.

Prove that

AZ² + BX² + CY² = AY² + CX² + BZ²

Solution:

Let us join OA, OB, and OC in the given figure.

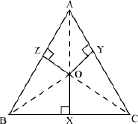
Using Pythagoras theorem in ΔOZA, we obtain

OA² = OZ² + AZ²

or AZ² = OA² − OZ² … (i)

Similarly, in ΔBOX and ΔCOY respectively, we obtain

BX² = OB² − OX² … (ii)

and CY² = OC² − OY² … (iii)

On adding equations (i), (ii) and (iii), we obtain

AZ² + BX² + CY² = OA² + OB² + OC² − OZ² − OX² − OY²

AZ² + BX² + CY² = (OA² − OY²) + (OB² − OZ²) + (OC² − OX²) … (iv)

Using Pythagoras theorem in ΔOYA, we obtain OA² = OY² + AY²

Or AY² = OA² − OY²

Similarly, BZ² = OB² − OZ² and CX² = OC² − OX²

Using these in equation (iv), we obtain AZ² + BX² + CY² = AY² + BZ² + CX²

Hence, proved.