2.Number of Tangents from a Point on the Circle

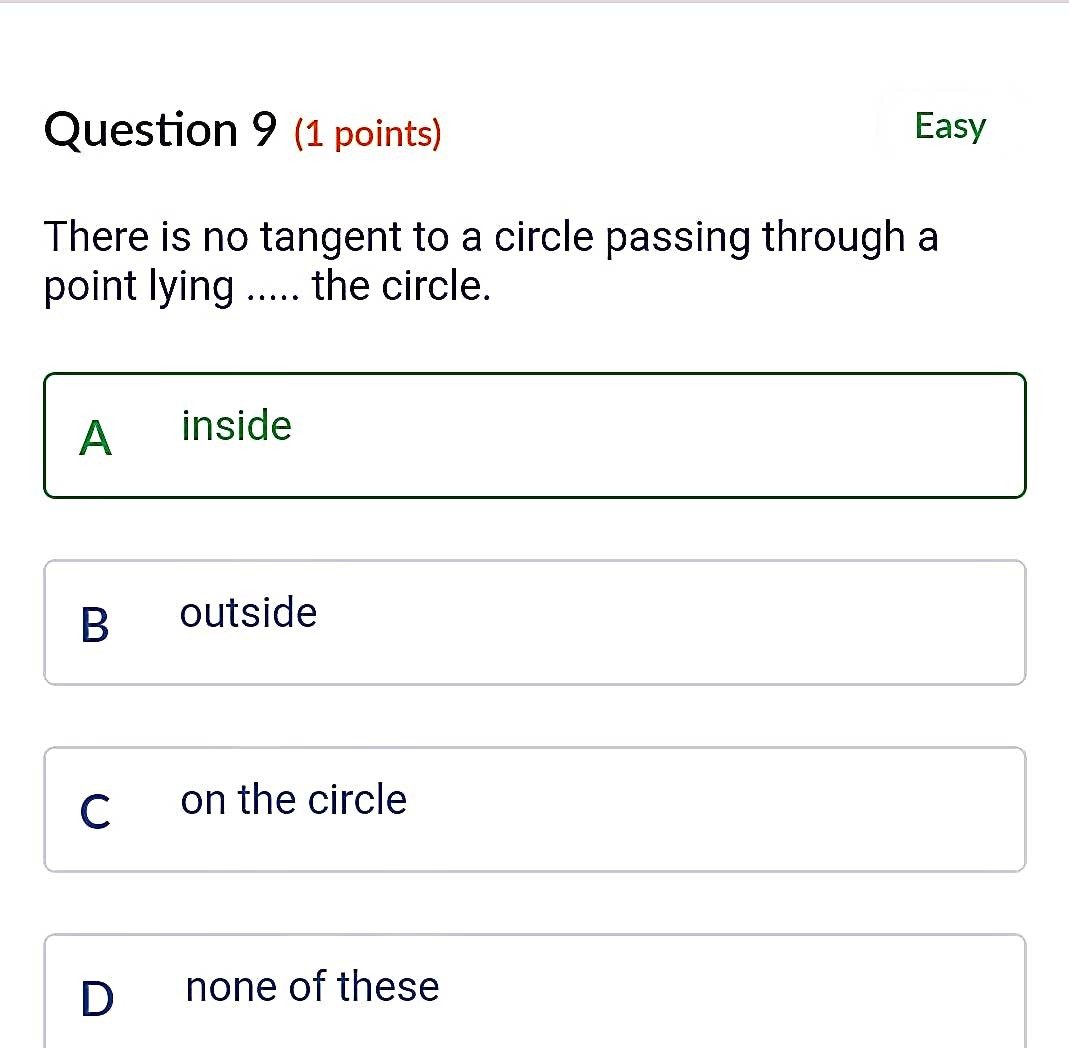
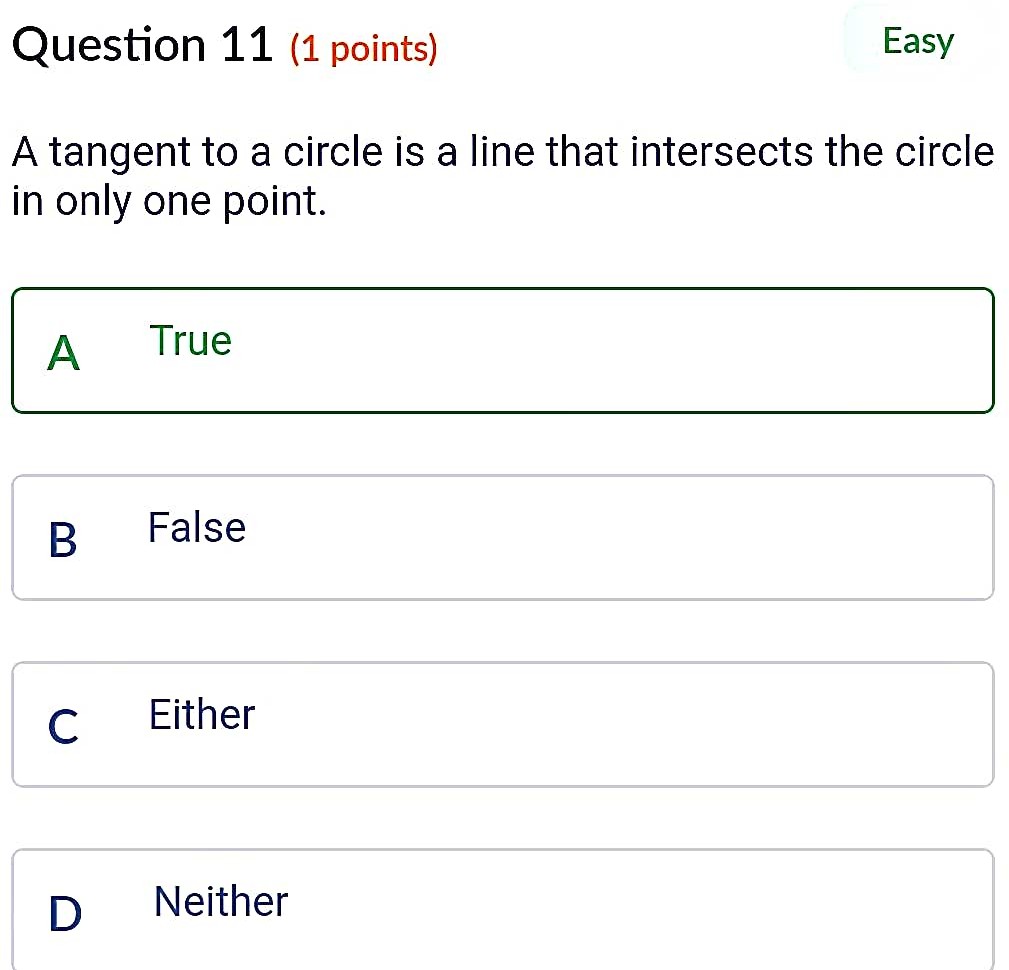
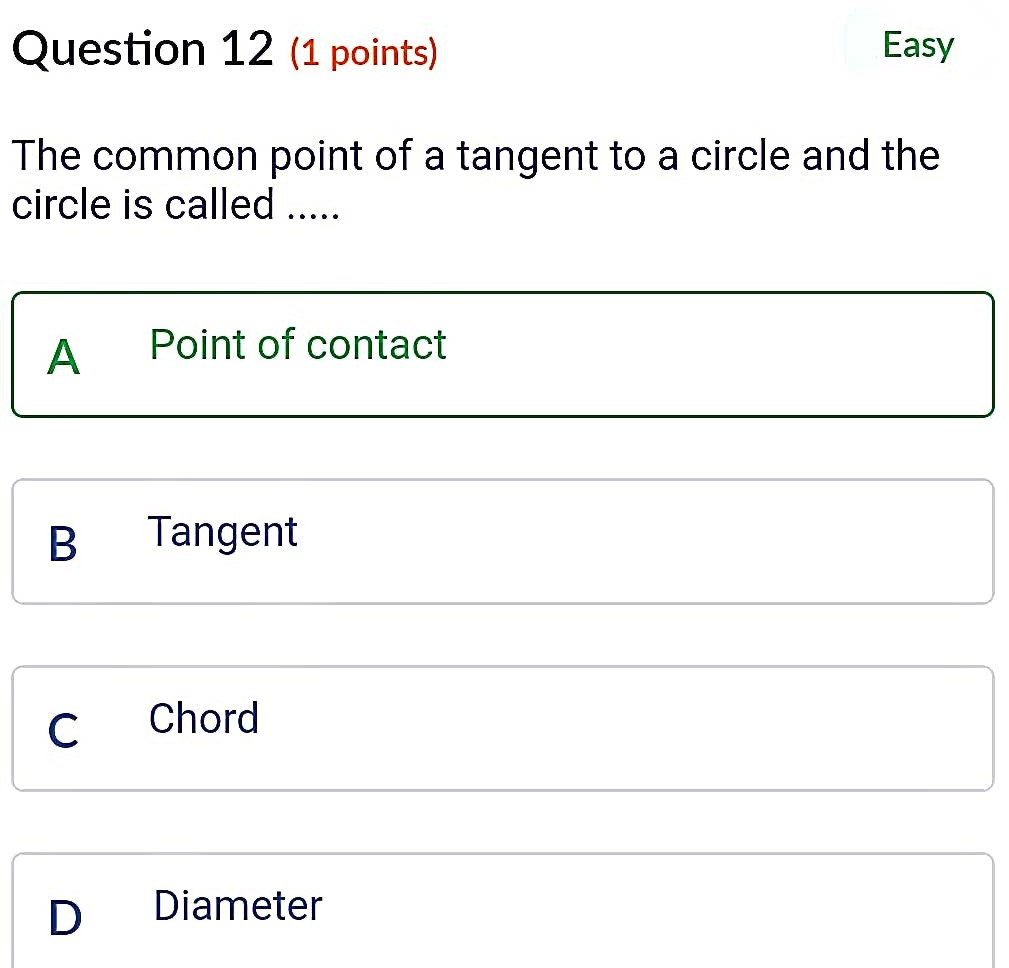
Tangents Drawn From An External Point To A Circle

We are very well aware of what a tangent is. Now let us look at the following video and find out how many tangents can be drawn to a circle from an external point and if there is any relation between the lengths of these tangents.

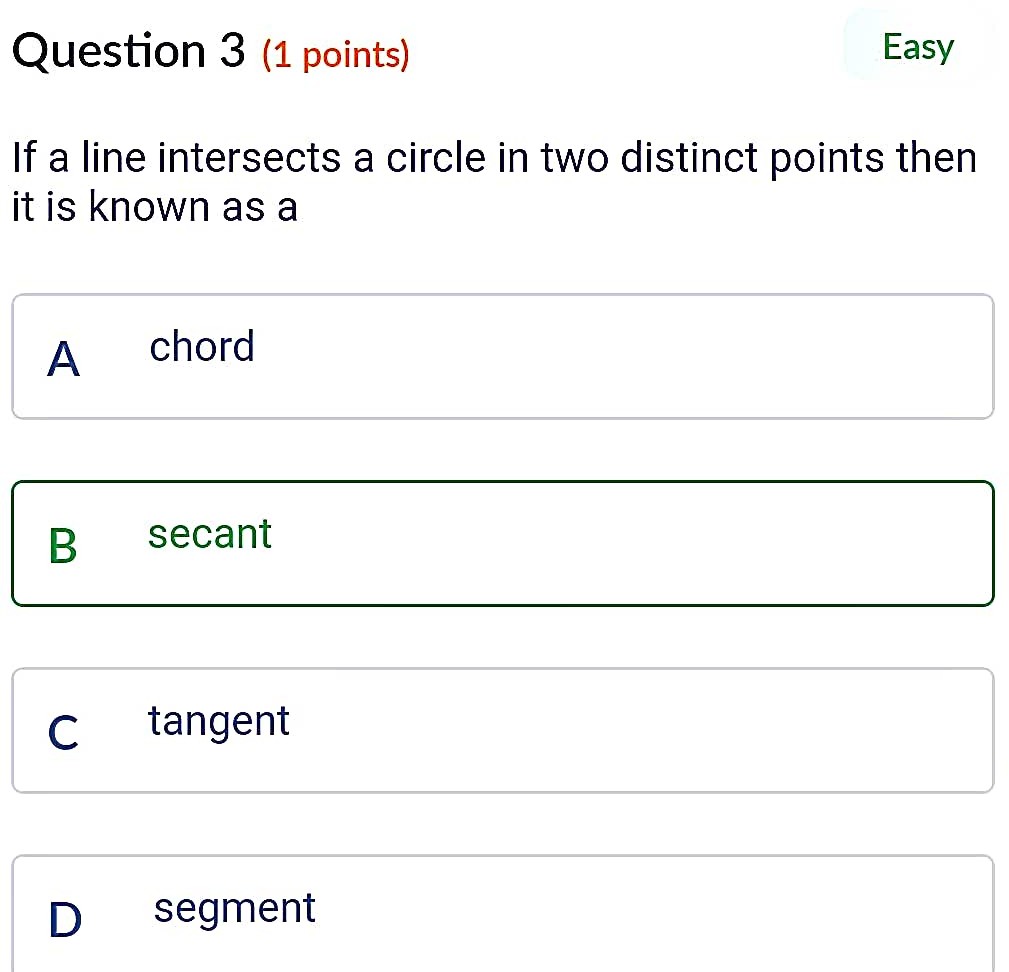
The lengths of the two tangent segments to a circle drawn from an external point are equal.

Proof:

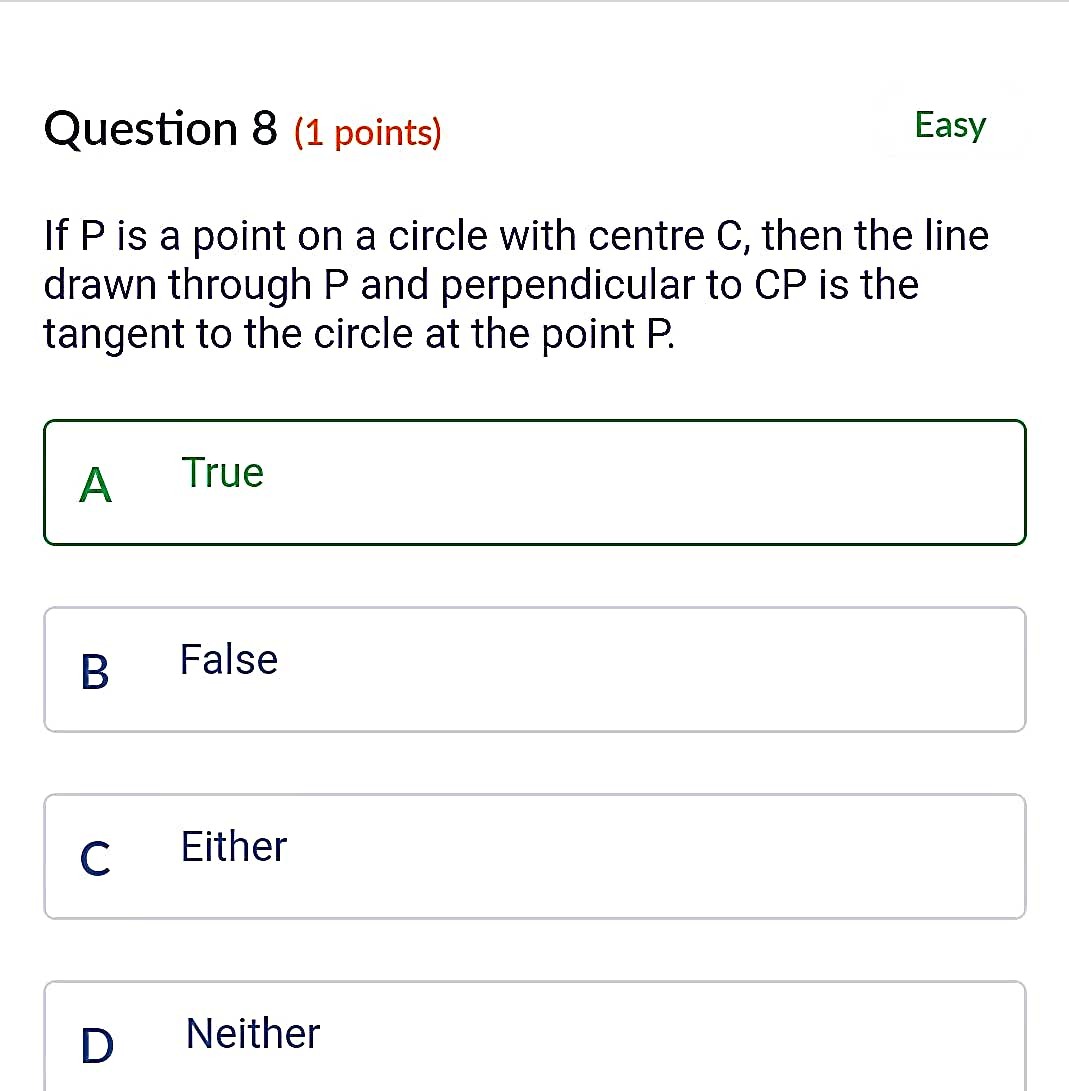
Let P be the point outside the circle having centre O from which the tangents PQ and PR are drawn touching the circle at Q and R respectively.

We have to prove that PQ = PR.

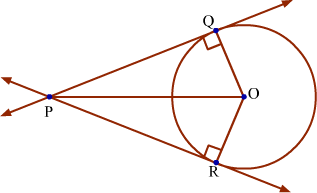
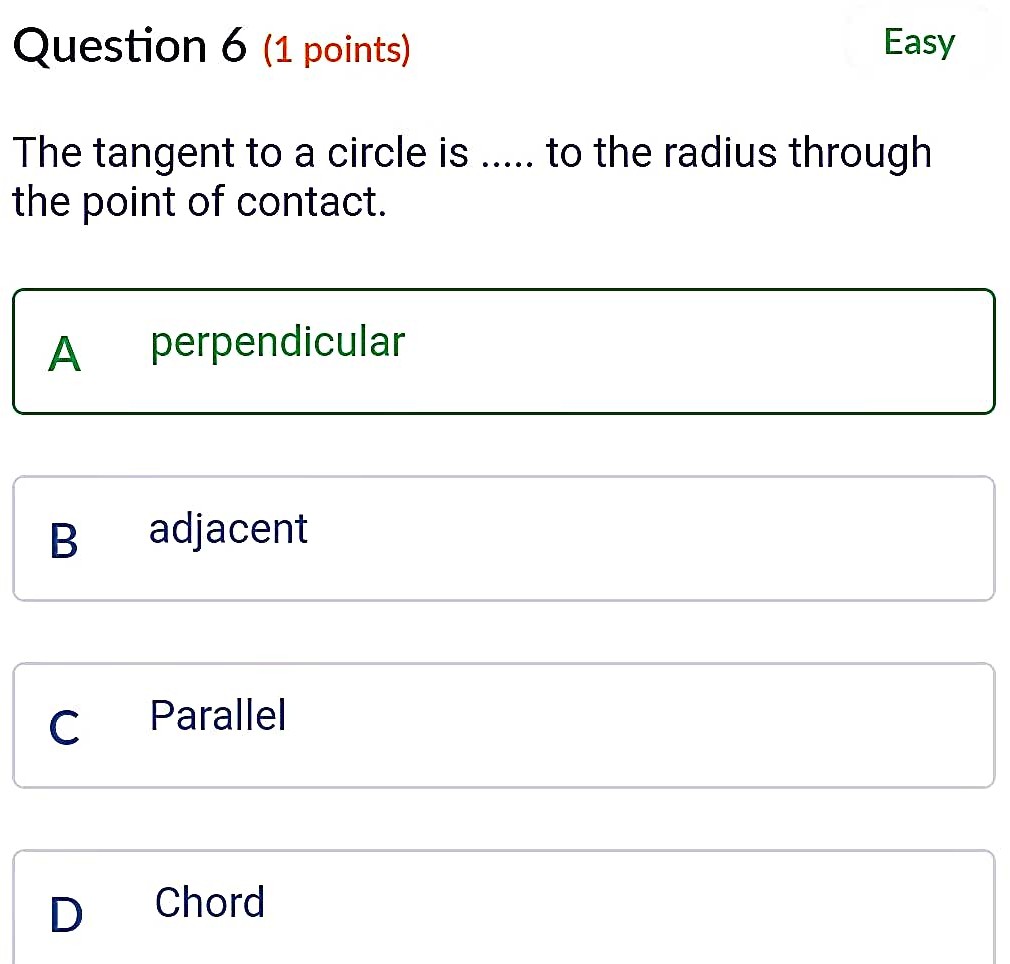
From the figure, it can be observed that OQ and OR are the radii of the circle. Therefore, ∠PQO = ∠PRO = 90°

Now, in ΔPOQ and ΔPOR, we have

∠PQO = ∠PRO = 90°

PO = PO (Common hypotenuse)

OQ = OR (Radii of same circle)

Using RHS (Right-Hypotenuse-Side) congruence rule, we get

ΔPOQ ΔPOR

∴ PQ = PR (By CPCT)

Thus, the lengths of the two tangent segments to a circle drawn from an external point are equal.

Note: Since ΔPOQ ΔPOR, we have

∠OPQ = ∠OPR (By CPCT)

∠POQ = ∠POR (By CPCT)

Thus, the above theorem can be extended as,

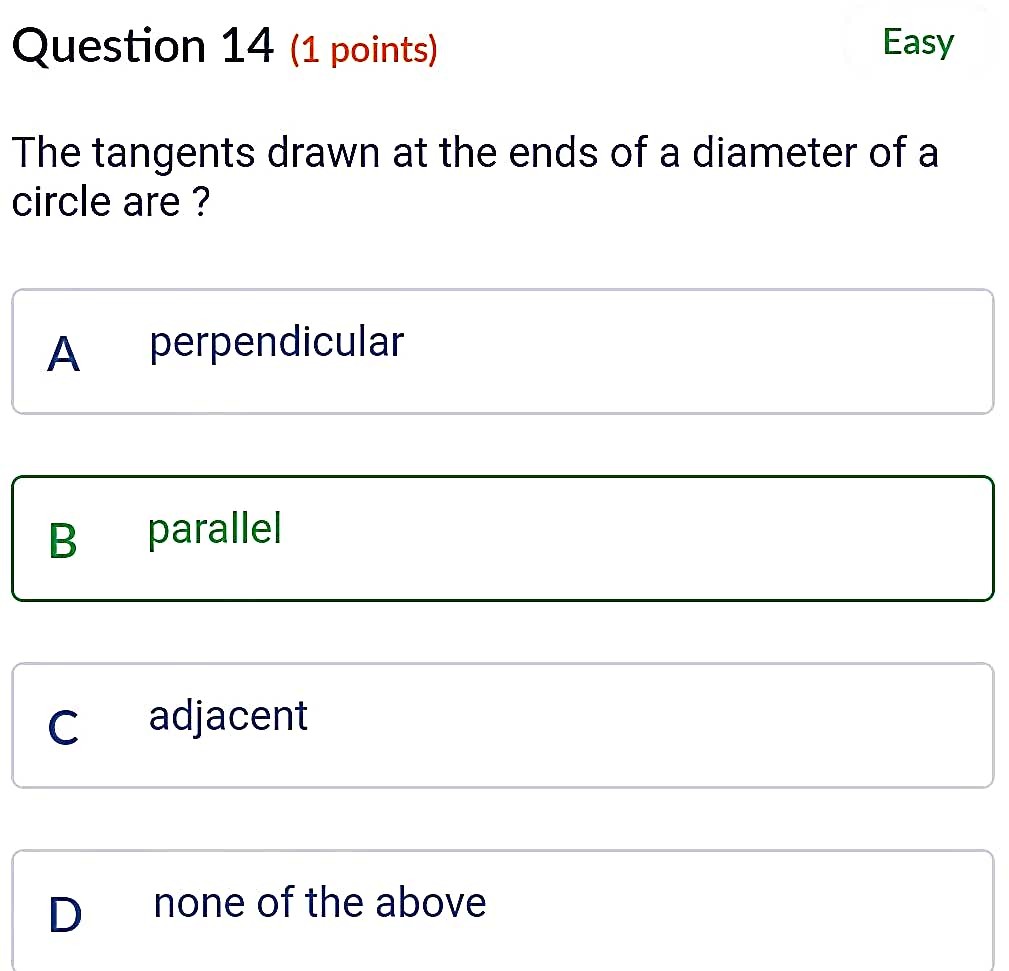
(1) The tangents drawn to a circle from an external point are equally inclined to the line joining the external point and the centre.

(2) The tangents drawn to a circle from an external point subtend equal angles at the centre.

Now, let us solve some examples to understand the concept.

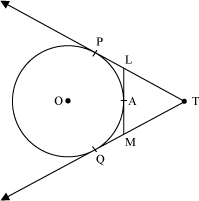
Example 1: In the given figure, prove that TL + AL = TM + AM

Example 2: A circle is circumscribed by a quadrilateral PQRS such that the circle touches all the sides of quadrilateral PQRS at points A, B, C, and D respectively. Show that

PQ + RS = QR + PS

Solution:

The figure can be drawn as follows.

Now, applying the theorem “The tangents drawn from an external point to the circle are equal in length”, we obtain

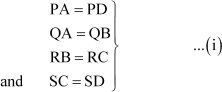
Therefore,

PQ + RS = (PA + QA) + (RC + SC)

= (PD + QB) + (RB + SD) [Using (i)]

= (PD + SD) + (QB + RB)

= PS + QR

Thus, PQ + RS = PS + QR

Hence, proved

Example 3: A circle is inscribed in a triangle ABC such that the circle touches the sides AB, BC, and AC of the triangle at P, Q, and R respectively. What are the lengths of AP, BQ, and CR if AB = 10 cm, BC = 6 cm, and AC = 12 cm.

Solution:

The figure can be drawn as follows.

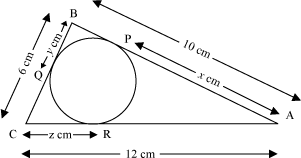
Let AP = x cm, BQ = y cm, and CR = z cm.

Now, applying the theorem “The tangents drawn from an external point to the circle are equal in length”, we obtain

AP = AR = x

BQ = BP = y

CR = CQ = z

Therefore, we can write

AP + BP = AB

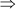x + y = 10 cm … (i)

BQ + QC = BC

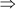y + z = 6 cm … (ii)

CR + AR = AC

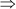z + x = 12 cm … (iii)

On adding (i), (ii), and (iii), we obtain

2x + 2y + 2z = 28 cm

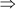x + y + z = 14 cm … (iv)

Subtracting (i) from (iv), we obtain

(x + y + z) – (x + y) = 14 – 10

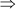z = 4 cm

Similarly, subtracting (ii) and (iii) respectively from (iv), we obtain

(x + y + z) – (y + z) = 14 – 6

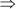x = 8 cm

(x + y + z) – (z + x) = 14 – 12

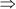y = 2 cm

Thus, AP = 8 cm, BQ = 2 cm, and CR = 4 cm

Example 4: In the given figure, PQR is an isosceles triangle with PQ = PR. A circle, which is inscribed in ΔPQR, touches the sides of the triangle at A, B, and C. Show that AQ = AR.

Solution:

It is given that PQR is an isosceles triangle where

PQ = PR … (i)

Now, the tangents drawn from an external point to a circle are equal in length.

∴ PC = PB … (ii)

On subtracting equation (ii) from equation (i), we obtain

PQ – PC = PR – PB

QC = RB … (iii)

Now, QA and QC are tangents to the circle from point Q.

∴ QA = QC

Similarly, RB = RA

Using the above relations in equation (iii), we obtain

QA = RA

∴ AQ = AR

Example 5: PA and QA are tangents drawn to a circle with centre O. Show that ∴BOQ

= ∴PAQ.

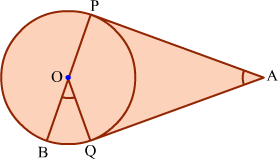
Solution:

Join O with A, P with Q.

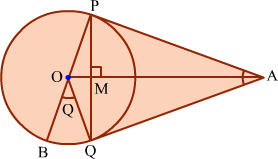
We know that, the tangents drawn to a circle from an external point are equal and they are equally inclined to the line joining the external point and the centre.

Therefore, ∠PAO = ∠QAO and ∠POA = ∠QOA.

It is clear that PQ ⊥ OA.

Now, ∠BOQ = 2∠OPQ … (1)

[Angle subtended by an arc at the centre is twice the angle subtended by the same arc at anywhere on the Circle]

Let ∠PAO = ∠QAO = θ. In ΔPMA,

From (1) and (2), ∠BOQ = 2θ. Therefore,

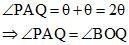
Hence, the result is proved.