1.Solution of Quadratic Equation by Factorisation

Introduction to Quadratic Equations

Consider the equations

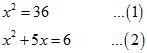
In equation (1), variable occurs only in second degree. The quadratic equations involving a variable only in second degree is a Pure quadratic equation.

Thus, an equation that can be expressed in the form 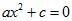, where a and c are real numbers and a ≠ 0 is a pure quadratic equation.

In equation (2) , variable occurs both in second and first degree. The quadratic equation involving a variable in both second and first degree is an Adfected quadratic equation.

Thus, an equation that can be expressed in the form 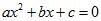, where a, b and c are real numbers and a ≠ 0 is an Adfected quadratic equation.

Now, let us learn about the roots of a quadratic equation.

Roots of a given quadratic equation are the values of the variables which satisfy that quadratic equation.

For example, consider the quadratic equation x² – 8x + 15 = 0. Here, L.H.S. = x2 – 8x + 15 and R.H.S. = 0

Let us substitute the different values of variable x in this equation and observe the results. When x = 1 then x² – 8x + 15 = 12 – 8(1) + 15 = 1 – 8 + 15 = 8 ∴ L.H.S. ≠ R.H.S.

When x = –1 then x² – 8x + 15 = (–1)² – 8(–1) + 15 = 1 + 8 + 15 = 24 ∴ L.H.S. ≠ R.H.S.

When x = 3 then x² – 8x + 15 = 3² – 8(3) + 15 = 9 – 24 + 15 = 0 ∴ L.H.S. = R.H.S.

When x = 4 then x² – 8x + 15 = 4² – 8(4) + 15 = 16 – 32 + 15 = –1 ∴ L.H.S. ≠ R.H.S.

When x = 5 then x² – 8x + 15 = 5² – 8(5) + 15 = 25 – 40 + 15 = 0 ∴ L.H.S. = R.H.S.

When x = –5 then x² – 8x + 15 = (–5)² – 8(–5) + 15 = 25 + 40 + 15 = 80 ∴ L.H.S. ≠ R.H.S.

It can be observed that for x = 3 and x = 5, we have L.H.S. = R.H.S. which means that the equation x² – 8x + 15 = 0 is satisfied. Thus, 3 and 5 are roots of this quadratic equation.

In other words, we can say that x = 3 and x = 5 are the solutions of quadratic equation x² – 8x + 15 = 0.

Also, for x = 1, x = –1, x = 4 and x = –5, we have L.H.S. ≠ R.H.S. which means that the equation x² – 8x + 15 = 0 is not satisfied. Thus, 1, –1, 4 and –5 are not the roots or solution of this quadratic equation.

Let us go through few examples to understand the concept better.

Example 1: Is the equation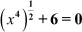 a quadratic equation?

Solution:

The given equation is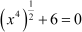

We can also write it as

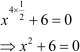
Hence, we can say that the given equation is a quadratic equation.

Example 2: Among the values given below find the roots of the quadratic equation 2x2 + 5x – 3 = 0.

x = 1, 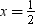, x = 2, x = –3,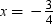

Solution:

We have,

Equation: 2x² + 5x – 3 = 0

Values: x = 1, 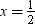, x = 2, x = –3,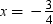

Let us substitute the given values of x in the equation and observe the results. When x = 1 then 2x² + 5x – 3 = 2(1)² + 5(1) – 3 = 2 + 5 – 3 = 4 ∴ L.H.S. ≠ R.H.S.

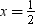When then

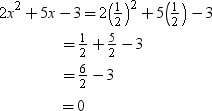
∴ L.H.S. = R.H.S.

When x = 2 then 2x² + 5x – 3 = 2(2)² + 5(2) – 3 = 8 + 10 – 3 = 15 ∴ L.H.S. ≠ R.H.S.

When x = –3 then 2x² + 5x – 3 = 2(–3)² + 5(–3) – 3 = 18 – 15 – 3 = 0 ∴ L.H.S. = R.H.S.

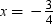When then

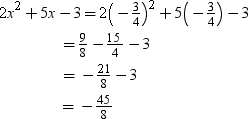
∴ L.H.S. ≠ R.H.S.

Only, 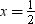and x = –3 satisfy the given quadratic equation.

Thus, 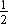and –3 are the roots of the given quadratic equation.

Example 3: If one root of the quadratic equation 3x² + 4x – p = 0 is 2323 then find the value of p.

Solution:

Since 2323 is a root of the equation 3x² + 4x – p = 0, it must satisfy the equation.

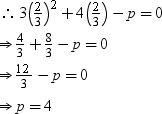
Example 4: State whether m is a root of the equation 2x² – (2m + 3)x + 3m = 0 or not.

Solution:

If m is a root of the equation 2x² – (2m + 3)x + 3m = 0 then it would satisfy the equation. Let us check it by substituting x = m in the given equation

2m² – (2m + 3)m + 3m

= 2m² – 2m² – 3m + 3m

= 0

∴ L.H.S. = R.H.S.

Hence, m is a root of the equation 2x² – (2m + 3)x + 3m = 0.

Expressing Given Situations as Quadratic Equations in One Variable

Quadratic equations arise in several situations around us and in different fields of mathematics. But how is a quadratic equation formulated?

Let us learn to express a situation mathematically.

Suppose there are two squares as shown in the following figure.

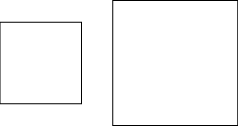
The sum of the areas of these two squares is 482 m² and the difference of their perimeters is 32 m. Can we form a quadratic equation for the given mathematical situation?

Example1: An express train takes 1 hour less than a passenger train to travel a distance of 132 km. If the average speed of the express train is 11 km/h more than that of a passenger train, then form a quadratic equation to find the average speed of the express train?

Solution:

Let the average speed of the express train be x km/h.

Since it is given that the speed of the express train is 11 km/h more than that of a passenger train,

Therefore, the speed of the passenger train will be x −11 km/h. Also we know that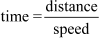

Time taken by the express train to cover 132 km =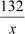

Time taken by the passenger train to cover 132 km =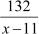

And the express train takes 1 hour less than the passenger train. Therefore,

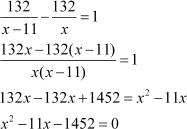
This is the required quadratic equation.

Example 2: A chess board contains 64 equal squares and the area of each square is 6.25 cm². A border 2 cm wide is made around the board. Formulate a quadratic equation to find the length of each side of the board?

Solution:

Let the length of each side of the chess board be x cm.

Therefore, the length of the chess board without border will be x − 4 cm as shown in the following figure.

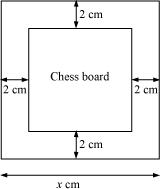
Area of the chess board without border = (x − 4)²

It is given that the area of each square is 6.25 cm².

Area of 64 squares on the chess board = 6.25 × 64

Therefore,

(x − 4)2 = 64 6.25

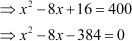
This is the required quadratic equation.

Solution of Quadratic Equations by the Method of Factorization

Quadratic equations come from many real life situations. Let us consider one such situation.

The area of a rectangular garden is 500 m² and its length is 5 m more than its breadth. Can we find the length and breadth of the garden?

The garden can be drawn as

Let the breadth of the garden be x m.

Then, according to the given information, its length must be (x + 5) m.

Now, area of the garden = length × breadth = (x + 5) × x

The area of the garden is given as 500 m².

∴ (x + 5) × x = 500

We can rewrite this equation as

x² + 5x = 500

⇒ x² + 5x – 500 = 0

This is a quadratic equation in variable x.

The length and the breadth of the garden can be calculated by solving the given quadratic equation.

How do we solve a quadratic equation? There are three methods of solving a quadratic equation, one of which is the method of factorization.

We have now expressed the equation x² + 5x – 500 = 0 as the product of two factors, (x + 25) and (x – 20). We can find the solutions of this equation by equating each factor to 0.

∴ x + 25 = 0 and x – 20 = 0

⇒ x = –25 and x = 20

However, the breadth of a park cannot be negative.

∴ x = 20

Thus, breadth of the park = 20 m and length of the park = (20 + 5) m = 25 m.

Let us now look at some more examples to get a grasp on this concept.

Example 1: Find the roots of the equation .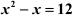

Solution:

First, we rearrange the given equation according to the standard format.

x² – x = 12

⇒ x² – x – 12 = 0

We need a pair of numbers whose product is –12 and whose sum is –1.

These numbers are 3 and –4.

We can now rewrite the equation as

x² – x – 12 = 0

⇒ x² + 3x – 4x – 12 = 0

⇒ x(x + 3) – 4(x + 3) = 0

⇒ (x – 4)(x + 3) = 0

The solutions of the given equation can now be determined by equating the two factors to 0.

∴ (x – 4) = 0 and (x + 3) = 0

⇒ x = 4 and x = –3

Thus, the two roots of the quadratic equation are 4 and –3.

Example 2: Find the roots of the equation .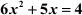

Solution:

First, we rearrange the given equation according to the standard format.

6x² + 5x – 4 = 0

Here, we need to find two such numbers whose product is 6 × (–4) = –24 and whose sum is 5.

The required numbers are 8 and –3.

Now, [8 × (–3) = –24 and 8 + (–3) = 5]

6x² + 5x – 4 = 0

⇒ 6x² + 8x –3x – 4 = 0

⇒ 2x(3x + 4) – 1(3x + 4) = 0

⇒ (2x – 1)(3x + 4) = 0

⇒ 2x – 1 = 0 and 3x + 4 = 0

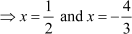
Thus, the roots of the given equation are .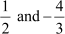

Example 3: Find two positive consecutive odd integers whose product is 99.

Solution:

Let the first integer be x.

The next odd integer will thus be x + 2.

∴ x(x + 2) = 99

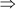x² + 2x – 99 = 0

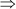x² + 11x – 9x – 99 = 0

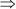x(x + 11) – 9(x + 11) = 0

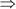(x – 9)(x + 11) = 0

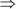x – 9 = 0 and x + 11 = 0

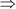x = 9 and x = –11

However, we know that the two integers are positive.

∴ x = 9

Thus, the two integers are 9 and (9 + 2) = 11.

Example 4: The width of a rectangle is 16 feet less than 3 times its length. If the area of the rectangle is 35 ft², then what are the dimensions of the rectangle?

Solution:

Here, the width of the rectangle has been expressed in terms of its length.

Hence, let us take the length of the rectangle to be x.

Thus, width of the rectangle = 3x – 16

The area of the rectangle is 35 ft².

∴ 35 = x(3x –16)

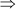35 = 3x² – 16x

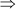3x² – 16x – 35 = 0

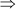3x² – 21x + 5x – 35 = 0

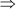3x(x – 7) + 5(x – 7) = 0

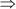(3x + 5)(x – 7) = 0

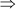3x + 5 = 0 and x – 7 = 0

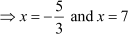
However, the length of a rectangle cannot be negative.

∴ x = 7

Thus, length of the rectangle is x = 7 ft and the width of the rectangle is 3x – 16 = (3 × 7 – 16) ft = 5 ft

Example 5: Difference between the ages of a father and his son is 22 years. If the product of their ages is 555 then what are their ages?

Solution:

Let the age of the son be x years.

Then age of the father will be 22 + x years.

Since the product of their ages is 555, we have

x(22 + x) = 555

⇒22x + x² = 555

⇒x² + 22x – 555 = 0

⇒x² + 37x – 15x – 555 = 0

⇒x(x + 37) – 15(x + 37) = 0

⇒(x + 37) (x – 15) = 0

⇒(x + 37) = 0 or (x – 15) = 0

⇒x = –37 or x = 15

Age cannot be negative, so we consider x = 15.

∴ Age of son = 15 years

∴ Age of father = (22 + 15) years = 37 years

Example 6: A bus takes 3 hours more than a train to travel a distance of 770 km. The speed of the train is more than that of bus by 15 km/hr. What are the average speeds of the bus and train?

Solution:

Let the average speed of the bus be x km/hr.

Then the average speed of the train will be (x + 15) km/hr.

Time taken by bus to cover 770 km =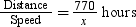

 Time taken by train to cover 770 km =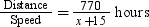

According to the question, we have

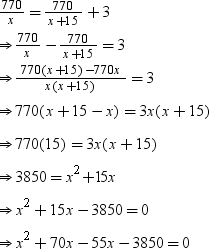
⇒ x(x + 70) – 55(x + 70) = 0

⇒ (x + 70) (x – 55) = 0

⇒ (x + 70) = 0 or (x – 55) = 0

⇒ x = –70 or x = 55

Speed cannot be negative, so we will consider x = 55.

∴ Average speed of bus = 55 km/hr

∴ Average speed of train = (55 + 15) km/hr = 70 km/hr