4.Pythagoras Theorem

Pythagoras Theorem and Its Applications

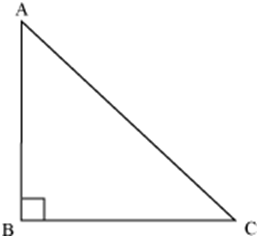
Look at the following right triangle ABC.

We have the following relationship between the sides of a right-angled triangle ABC. (AC)² = (AB)² + (BC)²

This relation between the sides of a right-angled triangle is known as Pythagoras Theorem.

This theorem has several other proofs also. Let us discuss two of them here.

Proof by American President:

The 20th president of United States, James Garfield proved this theorem taking two right angled triangles having sides as a, b and c and an other right angled triangle with side c.

The proof given by him is as follows:

All three triangles are combined as shown in the following figure.

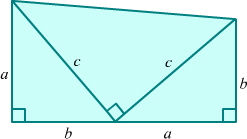
Thus, we got a trapezium.

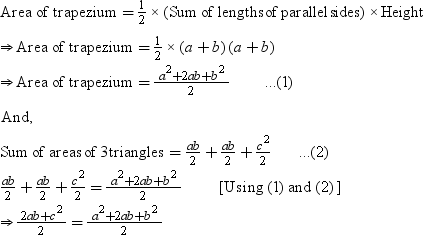
⇒ 2ab + c² = a² + 2ab + b²

⇒ c² = a² + b²

This theorem of right angled triangles was also known to Indian, Chinese, Greek and Babylonian mathematician long before Pythagoras lived. Thus, it was proved by the mathematicians of that time differently.

Proof by Indian Mathematician:

Bhaskaracharya, the great Indian mathematician of 2^nd century AD, used the below given diagrams to prove this theorem.

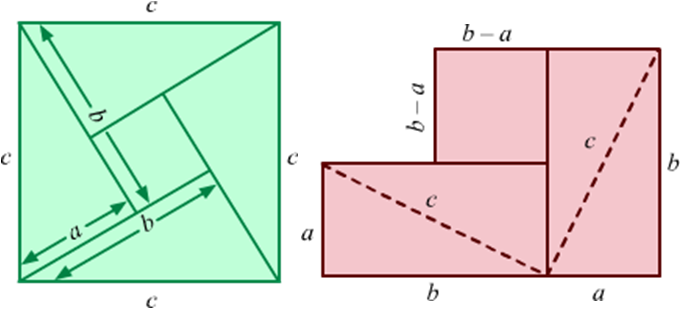
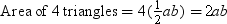
Area of small square = (b – a)² = b² – 2ab + a²

Area of big square = Area of 4 triangles + Area of small square

⇒ c² = 2ab + (b² – 2ab + a²)

⇒ c² = 2ab + b² – 2ab + a²

⇒ c² = b² + a²

Bhaskaracharya proved this theorem by using property of similarity also, but we will not discuss it here.

Note: Conventionally in ΔABC, we consider the lengths of sides opposite to vertices A, B and C as a, b and c respectively.

In real life, we come across many situations where a right angle is formed. Let us consider such a situation.

A 10m long ladder is placed on a wall such that the ladder touches the wall at 8m above the ground. This situation can be shown geometrically as follows.

In the above figure, AB is the wall of height 8 m and AC is the ladder of length 10 m. We know that a wall is perpendicular to the floor, i.e. AB is perpendicular to BC. Thus, ∠ABC is a right angle.

Now, can we calculate the distance of the foot of the ladder from the base of the wall?

We can calculate the distance of the foot of the ladder from the base of the wall by using Pythagoras theorem.

In this way, we can use Pythagoras theorem in many situations where right-angled triangle is formed.

Is the converse of Pythagoras theorem also true? Yes, the converse of Pythagoras theorem is also true. Its converse can be stated as follows:

“In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite to the first side is a right angle”.

But how will we prove it?

Thus, in a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite to the first side is a right angle.

Using the converse, we can check whether the given triangle is a right triangle or not.

Let ABC be a triangle with sides AB = 2.5 cm, BC = 6 cm and CA = 6.5 cm. Can we say that the triangle ABC is a right-angled triangle?

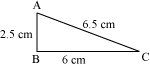
Here, (AB)² = (2.5)² = 6.25

(BC)² = 6² = 36

And, (CA)² = (6.5)² = 42.25

Therefore, we obtain

(AB)² + (BC)² = 6.25 + 36 = 42.25 = (CA)²

Thus, using the converse of Pythagoras theorem, we can say that the angle opposite to the side CA, i.e. ∠B, is a right angle.

Pythagorean triplet: Any three natural numbers a, b, c form a Pythagorean triplet if it satisfies a² = b² + c² irrespective of order.

General form to find the Pythagorean Triplets:

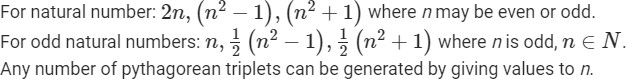
For example, the number 39, 80, and 89 forms a Pythagorean triplet.

39² = 1521

80² = 6400

89² = 7921

Now, 1521 + 6400 = 7921

∴39² + 80² = 89²

Here, the square of a number is equal to the sum of the squares of the other two numbers. Therefore, we can say that 39, 80, and 89 forms a Pythagorean triplet.

Applications of Pythagoras theorem:

Though Pythagoras theorem holds true for only right angled triangle, it can be applied to obtuse and acute angled triangles as well. The obtained results are discussed below:

{1] In acute angled ΔPQR , if PS ∠ QR, QSR is a line and ∠Q < 90° then

PR² = PQ² + QR² – 2QR . QS

Proof: Observe the acute angled triangle ΔPQR.

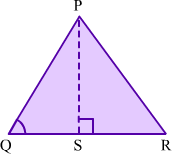
Here, PS ⊥ QR, QSR is a line and ∠Q < 90°.

In ΔPSQ, we have

PQ² = PS² + QS² ...(1) (By Pythagoras theorem)

In ΔPSR, we have

PR2 = PS² + SR² (By Pythagoras theorem)

⇒ PR² = PS² + (QR – QS)²

⇒ PR² = PS² + QR² + QS² – 2QR . QS

⇒ PR² = (PS² + QS²) + QR² – 2QR . QS

⇒ PR² = PQ² + QR² – 2QR . QS [Using (1)]

Hence proved.

(2)    In obtuse angled ΔPQR , if PS ∠ QR, SQR is a line and ∠Q > 90° then

PR² = PQ² + QR² + 2QR . QS

Proof:

Observe the acute angled triangle ΔPQR.

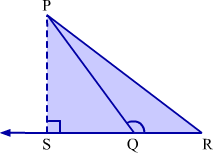
Here, PS ⊥ QR, SQR is a line and ∠Q > 90°.

In ΔPSQ, we have

PQ² = PS² + QS² ...(1)

(By Pythagoras theorem) In

ΔPSR, we have

PR² = PS² + SR² (By Pythagoras theorem)

⇒ PR² = PS² + (QR + QS)²

⇒ PR² = PS² + QR² + QS² + 2QR . QS

⇒ PR² = (PS² + QS2) + QR² + 2QR . QS

⇒ PR² = PQ² + QR² + 2QR . QS [Using (1)]

Hence proved.

Now, let us discuss some more examples based on Pythagoras theorem and its converse.

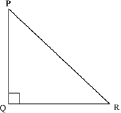
Example 1: ΔPQR is an isosceles triangle, right angled at Q. Prove that PR² = 2PQ².

Solution:

Here, PQR is an isosceles triangle, right angled at Q. Therefore,

PQ = QR … (1)

Now, using Pythagoras theorem, we obtain

(PR⁾² = (PQ)² + (QR)²

Using equation (1), we obtain

(PR)² = (PQ)² + (PQ)²

(PR)² = 2(PQ)²

Example 2: Two poles are of length 5m and 11m. The distance between the feet of the poles is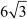 m. Find the distance between the tops of the poles.

Solution:

The figure for the given situation can be drawn as follows.

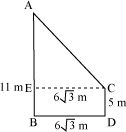
In the above figure, the poles are denoted by AB and CD, where AB = 11 m and CD = 5 m. The distance between the feet of the poles, i.e. BD, is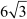 m.

Let us draw a perpendicular CE from C on AB

. AC is the distance between the top of the poles.

Here, BD = CE = 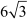m

And AE = AB− BE

= AB − CD [since BE = CD]

= (11 − 5) m

= 6 m

Using Pythagoras theorem in ΔACE, we obtain

(AC)² = (AE)² + (EC)²

(AC)2 = (6)2 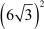m² + m²

= (36 + 108) m²

= 144 m²

⇒ AC =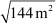

⇒ AC = 12 m

Thus, the distance between the tops of the poles is 12 m.

Example 3: O is any point in the interior of ΔABC and OX, OY, and OZ are the perpendiculars drawn from O to BC, CA, and AB respectively.

Prove that

AZ² + BX² + CY² = AY² + CX² + BZ²

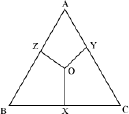
Solution:

Let us join OA, OB, and OC in the given figure.

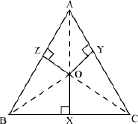
Using Pythagoras theorem in ΔOZA, we obtain

OA² = OZ² + AZ²

or AZ² = OA² − OZ² … (i)

Similarly, in ΔBOX and ΔCOY respectively, we obtain

BX² = OB² − OX² … (ii)

and CY² = OC² − OY² … (iii)

On adding equations (i), (ii) and (iii), we obtain

AZ² + BX² + CY² = OA² + OB² + OC² − OZ² − OX² − OY²

AZ² + BX² + CY² = (OA² − OY²) + (OB² − OZ²) + (OC² − OX²) … (iv)

Using Pythagoras theorem in ΔOYA, we obtain OA² = OY² + AY²

Or AY² = OA² − OY²

Similarly, BZ² = OB² − OZ² and CX² = OC² − OX²

Using these in equation (iv), we obtain AZ² + BX² + CY² = AY² + BZ² + CX²

Hence, proved.