Chapter 7: Coordinate geometry

Distance Formula

Let us consider the following graph.

In the above figure, O is the origin, A is a point at a distance of 3 units on x-axis, and B is a point at a distance of 4 units on y-axis.

Can we find the distance between the two points A and B?

In coordinate geometry, the distance formula has a lot of applications. Let us look at one of its applications.

What can you say about the three points (–6, 10), (–1, 1), and (3, –8)? Are they collinear?

Let us see.

If the sum of the distances of any point from the other two is equal to the distance between the other two points, then we can say that the given points are collinear.

For example, let (–6, 10), (–1, 1), and (3, –8) be denoted by A, B, and C respectively.

Now, using distance formula,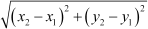 , we obtain

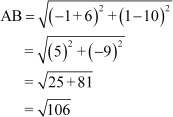
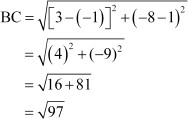
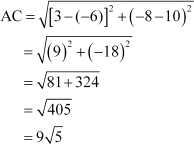
Here, AB + BC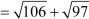

≠ AC

Therefore, the points A, B, and C are not collinear.

Let us solve some more examples based on the distance formula.

Example 1: Find the distance between the point (7, –1) and origin.

Solution:

Let the points (7, –1) and origin (0, 0) be denoted by A and O respectively. Then, using distance formula, we obtain

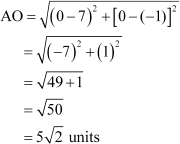
Thus, the distance between the points (7, –1) and (0, 0) is 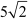units.

Example 2: Find the value of a, if the distance between (a, –1) and (8, 3) is .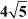

Solution:

Let points (a, –1) and (8, 3) be denoted by A and B respectively. Then, using distance formula, we obtain

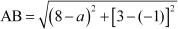
The distance is given as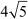 . Therefore, we can write

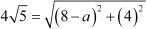
On squaring both sides, we obtain

16 × 5 = 64 + a² – 16a + 16

⇒ 80 – 64 – 16 = a² – 16a

⇒ 80 – 80 = a² – 16a

⇒ a² – 16a = 0

⇒ a (a – 16) = 0

∴ a = 0 and 16

Thus, the values of a are 0 and 16.

Example 3: Find the point on y-axis that is equidistant from (–5, 2) and (9, –2).

Solution:

The x-coordinate of all points on the y-axis is zero. Therefore, let (0, b) be the point which is equidistant from (–5, 2) and (9, –2).

∴ Distance between (0, b) and (–5, 2) = Distance between (0, b) and (9, –2) Using distance formula, we obtain

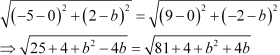
On squaring both sides, we obtain

29 + b² – 4b = 85 + b² + 4b

⇒ 8b = 29 – 85

⇒ 8b = –56

⇒ b = –7

Thus, the point (0, –7) on the y-axisis equidistant from (–5, 2) and (9, –2).

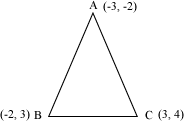
Example 4: Check whether the points (–3, –2), (–2, 3), and (3, 4) are the vertices of an isosceles triangle or not.

Solution:

Let the vertices (–3, –2), (–2, 3), and (3, 4) be denoted as A, B, and C respectively as shown in the figure.

Using distance formula, we obtain

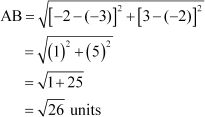
BC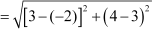

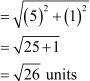
AC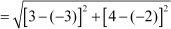

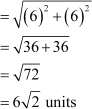
Now, AB = BC = 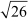units

Thus, (–3, –2), (–2, 3), and (3, 4) are the vertices of an isosceles triangle.

Distance formula

✓(x1~x2)²+(y1~y2)²

Find distance between points A(2,1) and B (3,6)

✓(3-2)²+(6-1)²

✓(1)²+(5)²

✓1+25=√26

Section Formula

Bageecha Singh’s garden is rectangular in shape and its length and breadth are 10 m and 20 m respectively. Two lamp posts in the garden are placed at the ends of a diagonal of the garden. Bageecha Singh wants to place one more lamp post between the two lamp posts that will divide the line segment joining the two lamp posts in the ratio 3:5.

Now, can you help him to find the position of the new lamp post? External division of a line segment:

Observe the figure given below.

Here, AB is a line segment and P is a point outside the line segment AB such that A – B – P (or P – A – B). So, it can be said that the point P divides the line segment AB externally in the ratio AB : BP. Point P is known as the point of external division.

Let the coordinates of points A and B be (x₁, y₁) and (x₂, y₂) respectively. Also, let the point P divide the line segment AB externally in the ratio m : n then the coordinates of point P are given by the following formula.

Coordinates of P =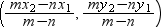

This formula is known as the section formula for external division.

are the vertices of a ΔABC, then the centroid of ΔABC is

Let us solve some examples based on the section formula.

Example 1: Find the coordinates of the point which divides the line segment joining the points (2, 3) and (–1, 7) internally in the ratio 1:2.

Solution:

Let (2, 3) and (–1, 7) be denoted by A and B respectively.

Let C be the point that divides the line segment AB internally in the ratio 1:2.

Using section formula, we obtain

Coordinates of C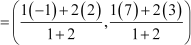

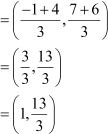
Thus,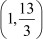 are the required coordinates of the point.

Example 2: Find the coordinates of the point which divides the line segment joining the points (4, –5) and (6, 2) externally in the ratio 3:2.

Solution:

Let (4, –5) and (6, 2) be denoted by A and B respectively.

Let P be the point that divides the line segment AB externally in the ratio 3:2. Using section formula, we obtain

Coordinates of P

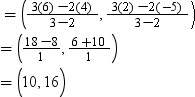
Thus, (10, 16) are the required coordinates of the point.

Example 3: Find the coordinates of the points of trisection of a line segment joining the points (−2, 1) and (4, –3).

Solution:

Let (–2, 1) and (4, –3) be denoted by A and B respectively.

Let C and D be the points of trisection. This means that C divides the line segment AB in the ratio 1 : 2 and D divides the line segment AB in the ratio 2 : 1.

Using section formula, we have

Coordinates of C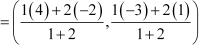

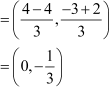
and Coordinates of D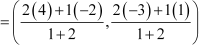

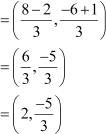
Thus, 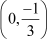and 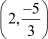are the points of trisection of a line segment joining the points (– 2, 1) and (4, –3).

Example 4: The mid-point of a portion of a line that lies in the first quadrant is (3, 2). Find the points at which the line intersects the axes.

Solution:

The line has been shown in the following graph:

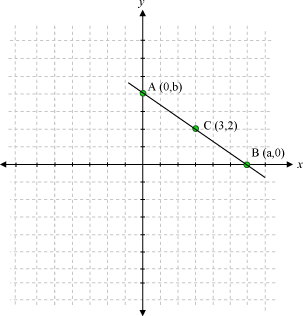
Let A and B be the points of intersection with y and x-axes respectively.

Let the coordinates of A and B be (0, b) and (a, 0).

Here, C is the mid-point of A and B.

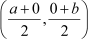∴ = (3, 2)

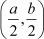= (3, 2)

On equating the x and y-coordinates on both sides, we obtain

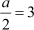and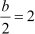

∴ a = 6 and b = 4

Thus, the coordinates of A and B are (0, 4) and (6, 0) respectively.

Area Of A Triangle In A Coordinate Plane

Let us consider a triangle whose base is parallel to x-axis.

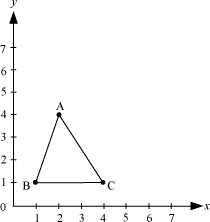
Can you find its area?

Yes, it is a simple question to us as we know that area of triangle is given by the formula

Area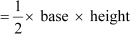

From the figure, it is clear that height of the triangle is 3 units and base is also 3 units.

Area of triangle ABC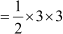

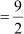square units

Now, consider the following figure

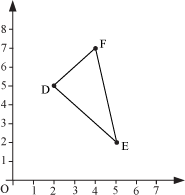
Now, can we calculate the area of ΔDEF? Here, we do not know the base and height. It is very difficult to find the base and height of ΔDEF but we can find the vertices of ΔDEF very easily.

The co-ordinates of D are (2, 5).

The co-ordinates of E are (5, 2).

The co-ordinates of F are (4, 7).

We can calculate the area of ΔDEF by a formula which involves the vertices of a triangle.

Let us derive that formula by considering any triangle, say ΔPQR, such that (x₁, y₁), (x₂, y₂), and (x₃, y₃) are the coordinates of the vertices P, Q and R respectively.

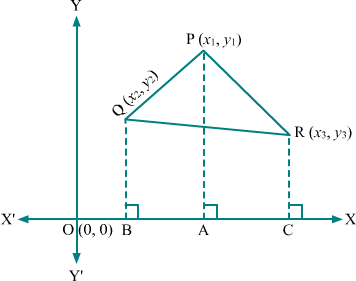
Here, line segments PA, QB and RC are the perpendiculars to X-axis from the vertices P, Q and R respectively. Therefore, PA || QB || RC and hence, quadrilaterals PQBA, PACR and QBCR are trapeziums.

From the figure, it can be seen that

Area of ΔPQR = Area of trapezium PQBA + Area of trapezium PACR – QBCR

We know that

Area of trapezium = 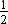(Sum of parallel sides × Perpendicular distance between parallel sides)

Therefore,

Area of ΔPQR = 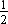(QB + PA)BA + 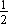(PA + RC)AC – 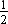(QB + RC)BC

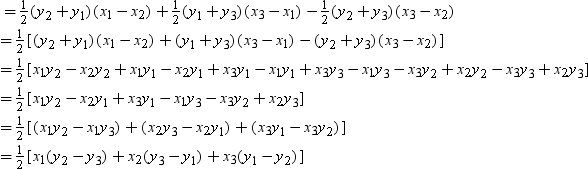
Now, let us find the area of ΔDEF using this formula.

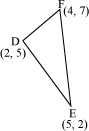
Area of triangle DEF

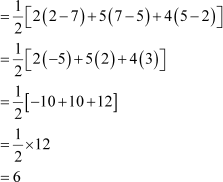
Area of ΔDEF = 6 square units

In this way, we can calculate the area of a triangle in a coordinate plane by using this formula.

Can we have a triangle with area 0 square units? Let us see this.

Let us find the area of a triangle formed by the vertices (1, 4), (−1, 1), and (3, 7).

Now, area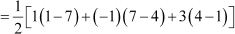

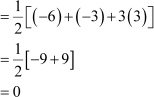
The area of the triangle is 0. What does it mean?

It means that the three given points are collinear.

Thus, “if area of a triangle is zero, then its vertices will be collinear”.

Let us solve some more examples.

Example 1: Find the area of a triangle whose vertices are (−3, −2), (−2, 3), and (3, 4).

Solution:

Let A (−3, −2), B (−2, 3), and C (3, 4) be the vertices of the triangle.

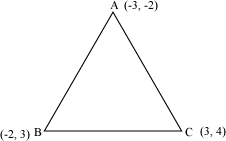
By using the formula,Area of triangle ,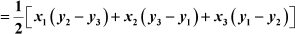

we obtain

Area of ΔABC

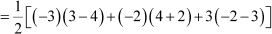
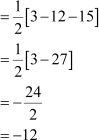
Neglecting the negative sign, we obtain

Area of triangle ABC = 12 square units

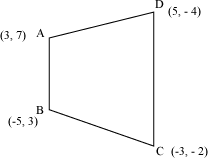
Example 2: Find the area of a quadrilateral whose vertices are (3, 7), (−5, 3), (−3, −2), and (5, −4) respectively? Solution:

Let ABCD be the quadrilateral as shown in the figure.

Draw a diagonal BD, which divides the quadrilateral into two triangles.

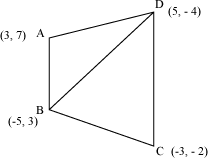
Now, area of quadrilateral ABCD = Area of ΔABD + Area of ΔBCD

Area of ΔABD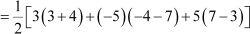

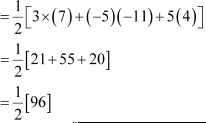
= 48 square units and area of ΔBCD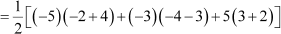

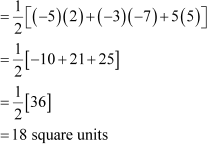
Area of quadrilateral ABCD = 48 + 18

= 66 square units

Thus, the area of quadrilateral ABCD is 66 square units.

Example 3: Find the value of x, if the points (0, 1), (x, −11), and (2, 9) are collinear.

Solution:

It is given that the points (0, 1), (x, −11), and (2, 9) are collinear. Thus, the area of triangle formed by these vertices will be zero.

Now, area of triangle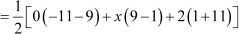

⇒ 0 =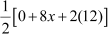

⇒

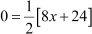
⇒ 8x + 24 = 0

⇒ 8x = −24

⇒ x = −3

Thus, the value of x is −3.