1.Trigonometric Ratios
Trigonometric Ratios
Suppose a boy is standing in front of a lamp post at a certain distance. The height of the boy is 170 cm and the length of his shadow is 150 cm.

You can see from the above figure that the boy and his shadow form a right-angled triangle as shown in the figure below.

The ratio of the height of the boy to his shadow is 170:150 i.e., 17:15.
Is this ratio related to either of the angles of ΔABC?
We can also conclude the following:
cos A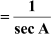 , tan A
, tan A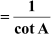
Also, note that
tan A = 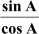 and cot A =
and cot A =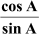
Let us now solve some more examples based on trigonometric ratios.
Example 1: In a triangle ABC, right-angled at B, side AB = 40 cm and BC = 9 cm. Find the value of sin A, cos A, and tan A.
Solution:
It is given that AB = 40 cm and BC = 9 cm

Using Pythagoras theorem in ΔABC, we obtain
(AC)2 = (AB)2 + (BC)2
(AC)2 = (40)2 + (9)2
(AC)2 = 1600 + 81
(AC)2 = 1681
(AC)2 = (41)2
AC = 41 cm
Now, sin A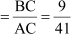
cos A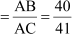
tan A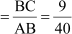
Example 2: From the given figure, find the values of cosec C and cot C, if AC = BC + 1.
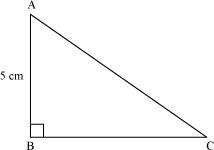
Solution:
Now, it is given that AB = 5 cm and
AC = BC + 1 … (1)
By Pythagoras theorem, we obtain
(AB)2 + (BC)2 = (AC)2
⇒ (AC)2 − (BC)2 = (AB)2
⇒ (BC + 1)2 – (BC)2 = (5)2 [Using (1)]
⇒ (BC)2 + 1 + 2BC – (BC)2 = 25
⇒ 2BC = 25 – 1
⇒ 2BC = 24
⇒ BC = 12 cm
∴ AC = 12 + 1 = 13 cm
Thus, cosec C =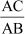
=![]()
And, cot C =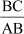
=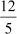
Example 3: In a right-angled triangle ABC, which is right-angled at B, tan A 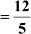 . Find the value of cos A and sec A.
. Find the value of cos A and sec A.
Solution:

It is given that tan A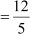
We know that tan A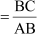
⇒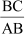
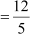
Let BC = 12k and AB = 5k
Using Pythagoras theorem in ΔABC, we obtain
(AC)2 = (AB)2 + (BC)2
= (5k)2 + (12k)2
= 25k2 + 144k2
(AC)2 = 169k2
AC = 13k
Now, cos A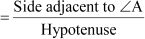
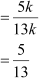
Sec A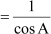
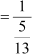
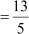
Use Trigonometric Ratios In Solving Problems
If we know the value of a trigonometric ratio, then we can find the values of other trigonometric ratios and the value of any expression involving these trigonometric ratios.
Example1: If cot A 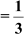 , then find the value of
, then find the value of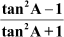 .
.
Solution:
It is given that cot A 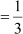 .
.
We know that
tan A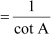
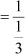
tan A = 3
Then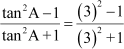 ,
,
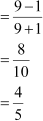
Example 2: Find the value of (sin2 θ + cos2 θ), if sec θ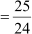 .
.
Solution:
We have sec θ 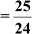 … (i)
… (i)
We know that sec θ 
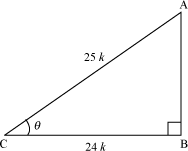
Let ABC be a triangle in which ∠C = θ, therefore we have
sec θ
From equations (i) and (ii), we have
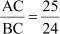
Let us take AC = 25k and BC = 24k.
Using Pythagoras theorem, we have,
(AC)2 = (AB)2 + (BC)2
(25k)2 = (AB)2 + (24k)2
625k2 = (AB)2 + 576k2
AB2 = (625 − 576)k2
AB2 = 49k2
AB = 7k
∴ sin θ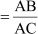
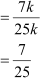
cos θ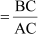
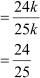
Now, sin2 θ + cos2 θ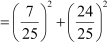
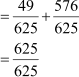
= 1
∴ sin2 θ + cos2 θ = 1
2.Trigonometric Ratios of Specific Angles
Trigonometric Ratios Of Some Specific Angles
Trigonometric ratios of some common angles such as 0°, 45°, 90°, etc. are used very often in solving trigonometric questions.
Example 1: Find the value of cos 2A if A = 30°. Solution:
It is given that A = 30°
∴ cos 2A = cos (2 × 30°)
= cos 60°
=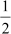
Example 2: Prove that sin 2A = 2 sin A cos A, for A = 45°.
Solution:
L.H.S = sin 2 A = sin (2 × 45°)
= sin 90 °
= 1
R.H.S. = 2 sin A cos A = 2 × sin 45° × cos 45°
= 2 ×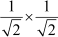
= 1
L.H.S = R.H.S.
∴ sin 2A = 2 sin A cos A
Example 3: From the given figure XYZ, find ∠YZX and ∠ZXY.
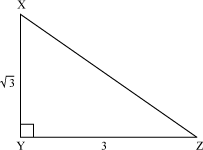
Solution:
It is given that XY =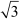 and YZ = 3
and YZ = 3
Now,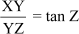
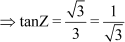
∴ ∠YZX = 30°
By angle sum property in ΔXYZ, we obtain
∠ZXY = 180° − 30° − 90°
∴ ∠ZXY = 60°
Example 4: If sin (A + B) = 1 and tan (A −B) = 0, where 0°< A + B ≤ 90°, then find A and B.
Solution:
sin (A + B) = 1,
We know that sin 90° = 1
⇒ A + B = 90° ... (1) tan (A −B) = 0
And, we know that tan 0° = 0
⇒ A − B = 0° ... (2)
On adding (1) and (2), we obtain 2A = 90°
⇒ A = 45°
On putting this value of A in (1), we obtain B = 45°
Thus, the value of both A and B is 45°.
Example 5: Find the value of 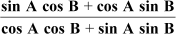 , if A = 60° and B = 30°.
, if A = 60° and B = 30°.
Solution:
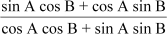 =
=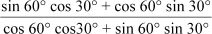
=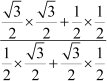
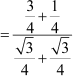
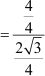
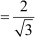
Example 6: Find the value of sin2 60° + 2 cos2 30° – tan2 45° + sec2 30°
Solution:
sin2 60° + 2 cos2 30° – tan2 45° + sec2 30°
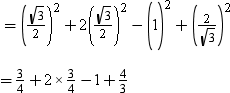
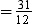
Example 7: If sin x = sin 60° cos 30° + cos 60° sin 30° then find the value of x.
Solution:
We have
sin x = sin 60° cos 30° + cos 60° sin 30°
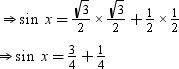
⇒ sin x = 1
⇒ sin x = sin 90°
⇒ x = 90°
Example 8: ABCD is a trapezium such that AB || CD and AD = BC.

Find the area of the trapezium.
Solution:
In right-angled ΔAED, we have
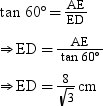
In ΔAED and ΔBFC, we have
AD = BC
∠AED = ∠BEC = 90° and
AE = BF (Perpendiculars drawn between two parallel lines)
∴ΔAED  ΔBFC
ΔBFC
By CPCT, we have
ED = FC = 83√83cm
ABFE is a rectangle, so we have AB = FE = 12 cm
Now, DC = ED + FE + FC = 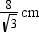 + 12 cm +
+ 12 cm + 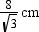 =
= 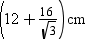
Area of trapezium ABCD = (AB + DC) × AE
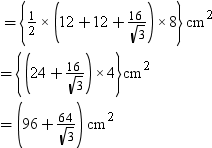
3.Trigonometric Ratios of Complementary Angles
Trigonometric Ratios Of Complementary Angles
Consider the following figure.

Here, a right-angled triangle ABC has been shown. In this triangle, suppose that the value of
sin C is 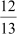 .
.
Can we find the value of cos A?
We can use these relations for simplifying the given expression.
For example: Let us express sec 55°− cosec 89° in terms of trigonometric ratios of angles between 0° and 45°.
Now, how can we do so? Let us see.
Since 55° and 35° are complementary angles and also 89° and 1° are complementary angles, we can write 55° as (90° − 35°) and 89° as (90° − 1°).
Therefore,
sec 55° − cosec 89° = sec (90° − 35°) − cosec (90° − 1°)
= cosec 35° − sec 1°
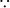 [ sec (90° – A) = cosec A and cosec (90° – A) = sec A]
[ sec (90° – A) = cosec A and cosec (90° – A) = sec A]
∴ sec 55° − cosec 89°= cosec 35° − sec 1°
Let us now solve some more examples involving trigonometric ratios of complementary angles.
Example 1: Find the value of sin 53° – cos 37°.
Solution:
We know that 53° and 37° are complementary angles as
53° + 37° = 90°
∴ We can write 37° as (90° – 53°).
∴ sin 53° – cos 37° = sin 53° – cos (90° – 53°)
= sin 53° – sin 53°
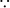 [ cos (90° – A) = sin A]
[ cos (90° – A) = sin A]
= 0
Thus, the value of (sin 53° – cos 37°) is 0.
Example 2: Evaluate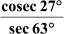
Solution:
Here, 27° and 63° are complementary angles as 27° + 63° = 90°
∴ We can write 27° = 90° – 63°
Now,
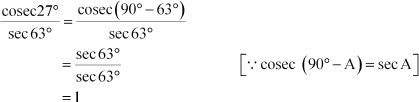
Example 3: Prove that tan 2A = cot 3A, when A = 18°.
Solution:
When A = 18°,
L.H.S = tan 2A = tan (2 × 18°)
= tan 36°
R.H.S = cot 3A = cot (3 × 18)
= cot 54°
54° and 36° are complementary angles.
∴ We can write 54° as 90° – 36°.
Therefore, cot 3A = cot 54°
= cot (90° – 36°)
= tan 36° [ 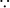 cot (90° – A) = tan A]
cot (90° – A) = tan A]
∴ L.H.S = R.H.S = tan 36°
∴ tan 2A = cot 3A
Example 4: If sin A = cos A, then prove that A = 45°.
Solution:
It is given that sin A = cos A
⇒ sin A = sin (90° – A)
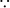 [ sin (90° – A) = cos A]
[ sin (90° – A) = cos A]
⇒ A = 90° – A
⇒ 2A = 90°
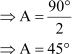
Hence, proved
Example 5: If P, Q, and R are interior angles of a triangle PQR, which is right-angled at Q, then show that
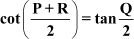
Solution:
Now, P, Q, and R are the interior angles of the triangle PQR. Therefore, their sum should be 180°.
∴ P + R = 180 – Q
Now, consider the L.H.S. =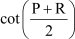
=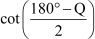
=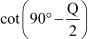
=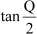 [
[ 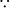 cot (90° – A) = tan A]
cot (90° – A) = tan A]
= R.H.S.
∴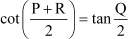
Hence, proved
Example 6: Prove that
tan1°× tan 2°× tan 3° … tan 87°× tan 88°× tan 89° = 1
Solution:
Here, 1° and 89° are complementary angles as 1° + 89° = 90°
Therefore, we can write 89° = 90° – 1°
Similarly, 88° = 90° – 2°
87° = 90° – 3°
46° = 90° – 44° and so on
Now, the L.H.S is
tan 1° × tan 2° × tan 3° … tan 44° × tan 45° × tan 46° … tan 87° × tan 88° × tan 89°
= tan 1° × tan 2° × tan 3° … tan 44° × tan 45° × tan (90° – 44°) … tan (90° – 3°) tan (90° – 2°)
tan (90° – 1°)
= tan 1° × tan 2° × tan 3° … tan 44° × tan 45° × cot 44° … cot 3° × cot 2° × cot 1°
[ 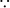 tan (90° – A) = cot A]
tan (90° – A) = cot A]
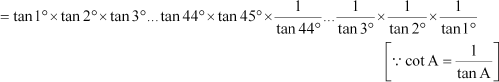
= tan 45°
= 1
= R.H.S
∴ tan1° × tan 2° × tan 3° … tan 87° × tan 88° × tan 89° = 1
Hence, proved
4.Trigonometric Identities
Trigonometric Identities
You have studied various algebraic identities so far. Similarly, we have various trigonometric identities, which are true for all variables.
Now, let us prove these identities.
Let us take a standard circle with radius r such that it intersects the X-axis at point A. Also, let the initial arm OA is rotated in anti-clockwise direction by an angle ?.
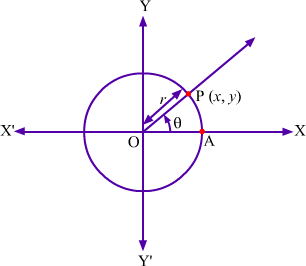
In the figure, the terminal arm intersects the circle at point P (x, y) where x, y ≠ 0 and OP = r. By the definition of trigonometric ratios, we have
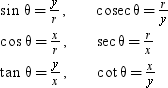
Now, OP is a distance between origin O (0, 0) and point P (x, y) which can be obtained by distance formula as follows:
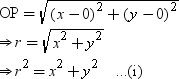
(1) On dividing both sides of the equation (i) by r2, we get
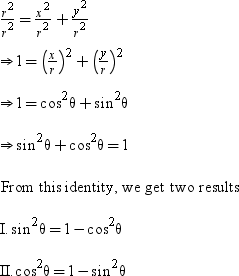
(2) On dividing both sides of the equation (i) by x2 (x ≠ 0), we get
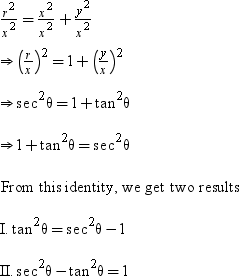
(3) On dividing both sides of the equation (i) by y2 (y ≠ 0), we get
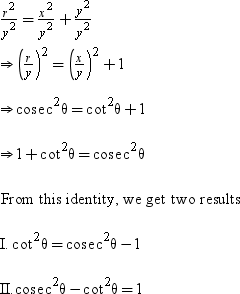
Corollary:
(i) When x = 0 then we have

In this case, the identities sin2θ + cos2θ = 1 and 1 + cot2θ = cosec2θ exist but the identity 1 + tan2θ = sec2θ does not exist.
(ii) When y = 0 then we have
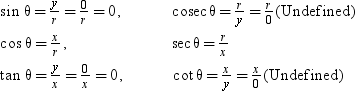
In this case, the identities sin2θ + cos2θ = 1 and 1 + tan2θ = sec2θ exist but the identity 1 + cot2θ = cosec2θ does not exist.
Now, we know the basic trigonometric identities, let us see the following video to know how to use these identities.
Example 1: Find the value of the expression (sec227° – tan27°.cot63°).
Solution:
sec227° – tan27°.cot63° = sec227° – tan27°.cot (90° – 27°)
[27° and 63° are complementary angles]
= sec227°– tan27°.tan27° [cot (90° – ?) = tan ?]
= sec227° – tan227°
= 1 + tan227° – tan2 27° [Using the identity 1 + tan2 θ = sec2 θ]
= 1
Thus, the value of the given expression is 1.
Example 2: Write all the trigonometric ratios in terms of sin A.
Solution:
Using the identity
sin2A + cos2A = 1,
we can write, cos2A = 1 – sin2A
Taking square root on both sides,
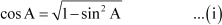
Now,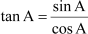
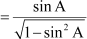 [Using (i)]
[Using (i)]
⇒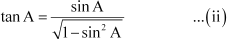
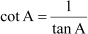
⇒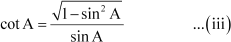
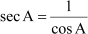
⇒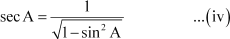 [Using (i)]
[Using (i)]
and,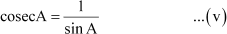
The trigonometric ratios in terms of sin A are given by (i), (ii), (iii), (iv), and (v).
Example 3: Simplify the following expression.
[(1 + cot A – cosec A)(1 + tan A + sec A)]
Solution:
(1 + cot A – cosec A)(1 + tan A + sec A)
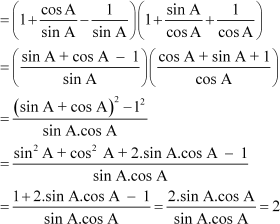
Thus, the value of the given expression is 2.
Use Of Trigonometric Identities In Proving Relationships Involving Trigonometric Ratios
Can we prove the following relation?
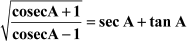
To prove this relation, we will make use of the following identities.
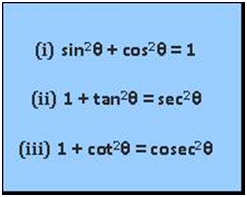
Let us see how to prove this.
We can take any side, L.H.S or R.H.S, of the above relation and prove it equal to the other side.
Now, L.H.S. =
= 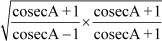 (by rationalising the denominator)
(by rationalising the denominator)
=
 = (Using the identity 1 + cot2θ = cosec2θ)
= (Using the identity 1 + cot2θ = cosec2θ)
=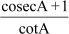
= sec A + tan A
= R.H.S.
Thus,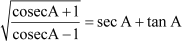
In this way, we use the above mentioned trigonometric identities to prove other relations involving trigonometric ratios.
Let us now look at another approach to solve a relation.
In this method, we simplify both L.H.S and R.H.S. and when we reach at a common point, we can say that the L.H.S. and R.H.S. are equal.
Let us try to prove that 2tan2A + tan4A = sec4A − 1.
Taking the L.H.S of the equation,
The L.H.S is given as 2tan2A + tan4A.
= tan2A (2 + tan2A)
= (sec2A − 1) (2 + sec2A − 1) [Using the identity 1 + tan2A = sec2A, we obtain tan2A = sec2A − 1]
= (sec2A − 1) (sec2A + 1)
The R.H.S is given by sec4A − 1.
= (sec2A − 1) (sec2A + 1) [a2 − b2 = (a − b) (a + b)]
Therefore, by solving both L.H.S and R.H.S, we obtain (sec2A − 1) (sec2A + 1).
Thus, we can say that 2tan2A + tan4A = sec4A − 1.
Now let us look at some more examples.
Example 1: Prove that 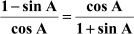 .
.
Solution:
L.H.S =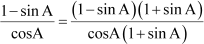
[Multiplying and dividing by (1 + sin A)]
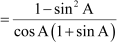
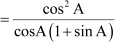 [Using the identity cos2A + sin2A = 1]
[Using the identity cos2A + sin2A = 1]
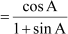
= R.H.S
∴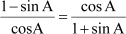
Example 2: Prove that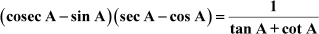
Solution:
L.H.S = (cosec A − sin A) (sec A − cos A)
= cosec A × sec A − cosec A × cos A − sin A × sec A + sin A × cos A
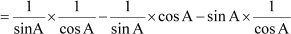 + sin A × cos A
+ sin A × cos A
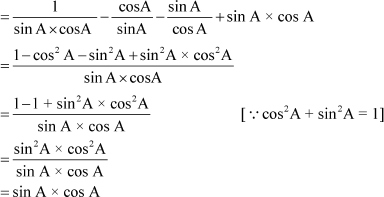
And R.H.S is given by
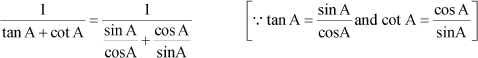
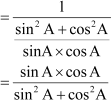
= sin A × cos A [∵sin2A + cos2A = 1]
Now L.H.S = R.H.S = sin A × cos A
∴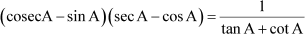

 ACERISE INDIA
ACERISE INDIA
