1.Perimeter and Area of a Circle
Areas Related to Circles
Length of Arc and Area of Sector of Circle
Some important formulae to remember are:
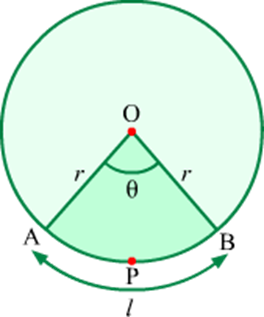

In case of quadrant, θ = 90°. Therefore,
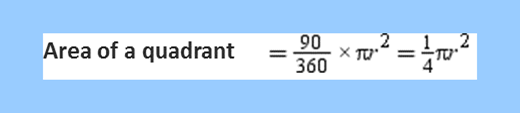
In case of semicircle, θ = 180°. Therefore,
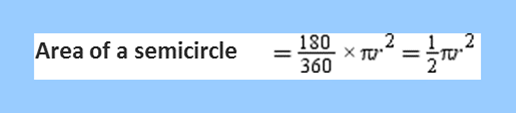
![]()
Relation between the area of sector and the length of an arc:
Look at the following figure.
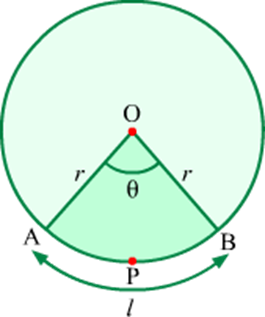
Here, O is the centre of the circle of radius r and APB is an arc of length l.
Clearly, measure of arc APB = Central angle = θ
Let the area of sector OAPB be A.
Now, we have

From length of arc and area of corresponding sector, we can also conclude that.
![]()
These formulae are very helpful to calculate various attributes related to circle. Let us solve some examples to learn the concept better.
Example 1: Find the area of the sectors OACB and OADB. Also find the length of the arc ACB. (Take π =![]() )
)
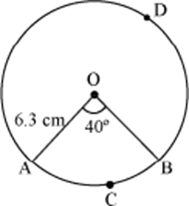
Solution:
Given, radius of the circle, r = 6.3 cm
Angle of sector OACB, θ = 40°
![]()
θ360×πr2
![]()
= 13.86 cm2
And, area of sector OADB = πr2 − area of the sector OACB
![]()
= 124.74 − 13.86 cm2
= 110.88 cm2
Length of arc ACB = ![]()
![]() = 4.4 cm
= 4.4 cm
Example 2: Find the area swept by the hour hand of length 10 cm of a clock when it moves from 2 p.m. to 4 p.m. Also find the length covered by the tip of the hour hand during that time. (Take π =3.14)
Solution:

When an hour hand moves from 2 p.m. to 4 p.m., it moves for 2 hours.
The hour hand takes 12 hours to complete 1 rotation i.e., to rotate 360°.
In 1 hour, it will rotate = ![]()
In 2 hours, it will rotate = 30° × 2 = 60°
Therefore, when it moves from 2 p.m. to 4 p.m., it sweeps an area equal to the area of a sector of angle 60°.
Radius of this sector = length of the hour hand = 10 cm
∴ Area swept ![]()
= 52.33 cm2 (approx.)
Length covered by the tip ![]()
= 10.47 cm (approx.)
Example 3: If the area and length of the arc of a sector are ![]() cm2 and
cm2 and ![]() cm respectively, then find out the radius of the circle and the angle of sector.
cm respectively, then find out the radius of the circle and the angle of sector.
Solution:
Let r be the radius of the circle and θ be the angle of sector.
It is given that the area of the sector is ![]() cm2.
cm2.
![]()
Also, the length of the arc is![]() cm.
cm.
⇒ ![]() =
=![]() … (2)
… (2)
On dividing Equation (1) with Equation (2), we obtain
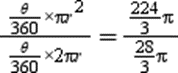
![]()
![]() cm
cm
On putting the value of r in equation (1), we obtain
= ![]()
![]()
![]()
Thus, the radius of the circle is 16 cm and the angle of the sector is 105°.
Example 4: Find the area of the sector OAXB and length of the arc AXB for the given figure.
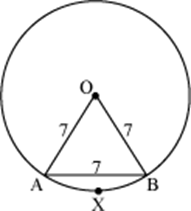
Solution:
In the figure, OA = AB = OB (All are of length 7 cm) Hence, ΔOAB is an equilateral triangle.
∴ ![]()
⇒ θ = 60°
Area of the sector = ![]() cm2
cm2
Length of the arc = ![]() cm
cm
Example 5: A truck has two wipers which do not overlap and each wiper has a blade of length 28 cm sweeping through an angle of 90°. What is the total area cleaned at each sweep of the blades?
Solution:
It is clear that each wiper sweeps a quadrant of a circle of radius 28 cm.
Area cleaned at each sweep =
Example 6: Radius of a circle is 14 cm. What is the area of the sector corresponding to the arc of length 20 cm?
Solution:
Radius of circle (r) = 14 cm
Length of arc (l) = 20 cm
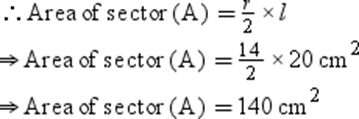
Example 7: Area of a sector of a circle whose radius is 12 cm is 132 cm2. Find the measure of central angle and length of the corresponding arc.
Solution:
Area of sector (A) = 132 cm2
Radius of circle (r) = 12 cm
Let the measure of central angle be θ and length of arc be l.
Now, we have
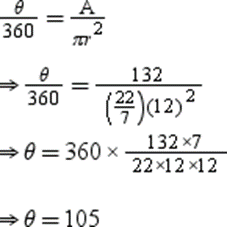
Thus, the central angle measures 105°.
Also, we have
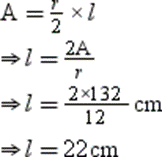
1.Perimeter and Area of a Circle
- Books Name
- Sample paper Term II Maths
- Publication
- SonikaAnandAcademy
- Course
- CBSE Class 10
- Subject
- Mathmatics
Perimeter of circle = 2πr
Area of circle =πr²
Find perimeter and area of circle for radius 7cm
Perimeter = 2π×7 = 14π cm
Area = πr²= π7×7= 49 π cm²
2.Area of Sector and Segment of a Circle
Area Of Segment Of A Circle
There is a design on a square window glass as shown below.

The shaded portion is coloured yellow. They are the segments of a circle whose radius is 7 cm and the angle of the sector is 90°. Rest all the portion is transparent. Can we calculate the area of the shaded portion?
To calculate the area of the shaded portion, we should know how to calculate the area of segments of the circle.
Firstly, let us know the formula to find the area of the segment of a circle.
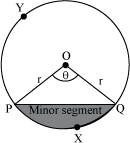
The above figure shows a circle with radius r. OPXQ is a sector of the circle. The angle of sector is θ. PXQP is a segment of the circle.
From the figure, we can see that
Area of the segment PXQP = area of the sector OPXQ − area of the triangle OPQ
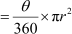 – area of ΔOPQ
– area of ΔOPQ
Using this formula, we can calculate the area of the shaded portion in the figure discussed in the beginning.
In that figure, the radius of the circle is given as 7 cm and angle of the sector 90°. To calculate the area of the shaded portion, we will calculate the area of each segment. Let us draw the circle whose segment has been shown in the given figure. On drawing the circle, we obtain the following figure.
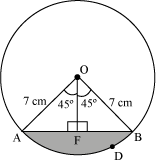
The sector has the angle 90° at the centre, i.e.  AOB = 90°.
AOB = 90°.
Let us draw a perpendicular from O to AB, i.e. OF  AB.
AB.
Now in Δ OAF and Δ OBF,
OA = OB (radius of the circle)
∠OFA = ∠OFB (both 90°)
OF = OF (common side)
By RHS Congruence rule,
ΔOAF ≅ ΔOBF
Therefore, AF = BF =  AB (by CPCT)
AB (by CPCT)
And ∠AOF = ∠BOF = 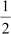 ∠AOB (by CPCT)
∠AOB (by CPCT)
=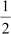 × 90° = 45°
× 90° = 45°
We know,
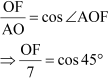
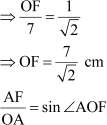
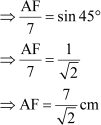
But we know that
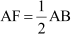
⇒ AB = 2 AF
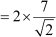 cm
cm
= 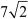 cm
cm
In ΔOAB,
Base = 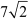 cm
cm
And corresponding height =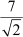 cm
cm
Thus, area of ΔOAB =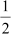 × base × height
× base × height
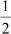 = ×
= ×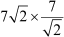
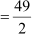 cm2
cm2
Given, r = 7 cm
θ = 90°
Thus, area of sector OADB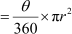
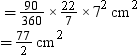
Therefore, area of the minor segment ADB
= Area of sector OADB − area of ΔOAB
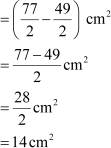
We have calculated the area of one such segment. But we have 4 such segments. Thus, the area of shaded portion is 56 cm2.
It can be seen that it was a very lengthy process to find the area of triangle in the above discussed case.
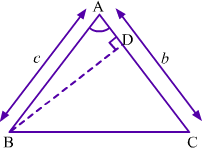
The area of triangle can be calculated in the other way as well. Let us see how. Let us consider ΔABC such that AB = c and AC = b.
BD is perpendicular to AC. Thus, BD is the height of ΔABC corresponding to base AC. In right-angled triangle ΔADB, we have
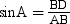
⇒ BD = AB sin A
⇒ BD = c sin A
Now,
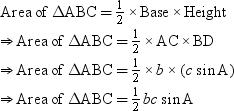
Similarly, we can find the area of the triangle inside the circle. Look at the following figure.
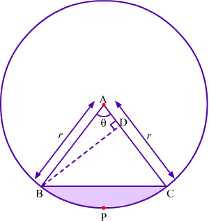
Here, AB = c = r, AC = b = r and ∠A = θ.
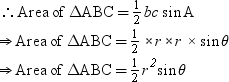
It can be seen that the area of triangle is in the form of radius of circle and central angle. For this figure, area of the segment BPC can be calculated as follows:
Area of segment BPC = Area of sector ABPC – Area of ΔABC
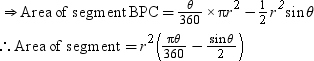
Using this formula, we can easily find the area of segment of circle of given radius. Let us solve some examples to understand this concept better.
Example1: Find the area of the segment ADB and AEB in the following figure. (Take π = 3.14)
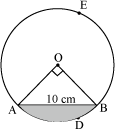
Solution:
In the above figure, chord AB = 10 cm and ∠AOB = 90°.
Now, we have to find out the radius of the circle.
We know that OA = OB (radii of the same circle)
ΔOAB is right-angled triangle as ∠AOB = 90°.
By using Pythagoras Theorem, we obtain
OA2 + OB2 = AB2
OA2 + OA2 = AB2
2OA2 = 102
2OA2 = 100
OA2 = 50
OA = 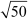 = 5
= 5 ![]() cm
cm
Hence, r = 5 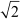 cm and θ = 90°
cm and θ = 90°
Area of minor segment ADB = Area of sector OADB − Area of ΔOAB
= 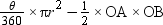
= 
=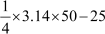
= 39.25 − 25
= 14.25 cm2
Area of the major segment AEB =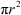 − area of the minor segment ADB
− area of the minor segment ADB
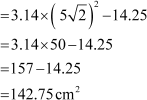
Thus, the area of segment ADB is 14.25 cm2 and the area of segment AEB is 142.75 cm2.
Example 2: In the given figure, O is the centre of the circle with radius 20 cm. Also, area of the shaded portion is 72.66 cm2 and the area of unshaded portion is 346 cm2. Find the measure of θ. ( = 3.14)
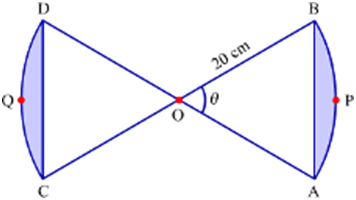
Solution:
It can be seen that the shaded portion has two equal segments APB and CQD of same circle with radius 20 cm whereas the unshaded portion has two equal triangles ΔAOB and ΔCOD.
Radius of circle (r) = 20 cm
∠AOB = ∠COD = θ
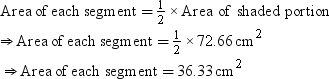
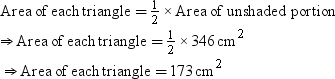
Area of segment APB = Area of sector OAPB – Area of ΔAOB
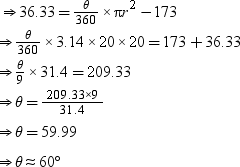
Example 3: In the given figure, O is the centre of the circle. Also, area of the shaded portion is 28.5 cm2. Find the area of the circle. (  = 3.14)
= 3.14)
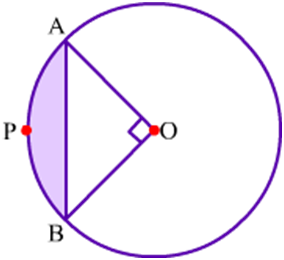
Solution:
We have,
θ = 90°
Area of segment = 28.5 cm2
Let the radius of the circle be r. Now,
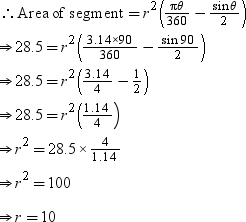
Thus, radius of circle is 10 cm.
Now,
Area of circle =  r2
r2
⇒ Area of circle = (3.14 × 10 × 10) cm2
⇒ Area of circle = 314 cm2
Area of Combination of Circles and Other Plane Figures
In our daily life, we come across various forms of interesting designs that are a combination of plane figures (like design on flower beds, windows, table covers etc.).
Suppose ABCD is a square land in a resort with side 200 m. There are four artificially created circular ponds of equal area in the land such that the perimeter of each pond touches two of the other three and also the perimeter of the land. The rough sketch of the land is shown below.

Can we calculate the area of the remaining portion of the land that is the area of the land without water?
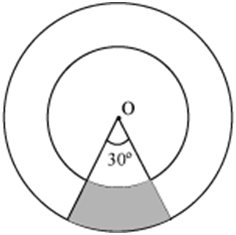
Example 1: In the following figure, there are two concentric circles. If the ratio of the radius of the larger c
ircle to that of the smaller circle is 3:2 and the length of the radius of the smaller circle is 14 cm, then find the area of the shaded portion. (Take π =![]() )
)
Solution
Let, the length of the radius of the larger circle be r1.
Given, length of the radius of the smaller circle, r2 = 14 cm
The ratio of the lengths of the radii is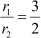
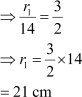
Now, area of the shaded portion = area of the sector of the larger circle with angle 30°
– area of the sector of the smaller circle with angle 30°
Area of the sector of the larger circle with angle 30° =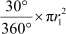
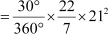
= 115.5 cm2
Area of the sector of the smaller circle with angle 30° =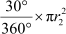
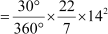
= 51.33 cm2 (approx.)
Therefore, area of the shaded portion = (115.5 − 51.33) cm2
= 64.17 cm2
Example 2: PQR is a right-angled triangle in which 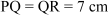 , ∠Q = 90°. If PSR is an arc of a circle with radius 7 cm and centre Q and PTR is a semi-circle with diameter PR, then find the area of the shaded portion.
, ∠Q = 90°. If PSR is an arc of a circle with radius 7 cm and centre Q and PTR is a semi-circle with diameter PR, then find the area of the shaded portion.

Solution:
Given, length of the radius of the circle, r = 7 cm
Also,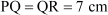
Hence, 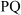 and
and 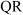 are the radii of the circle.
are the radii of the circle.
Given, ∠Q = 90°.
Thus, the portion described by QPSR is a quadrant of the circle with radius 7 cm.
Area of the quadrant QPSR =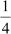 × area of the circle with radius 7 cm
× area of the circle with radius 7 cm
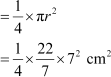
= 38.5 cm2
On applying Pythagoras theorem in the right-angled triangle PQR, we obtain
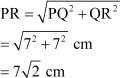
Now, area of the semi-circle PTR =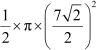
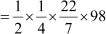
= 38.5 cm2
Area of the triangle PQR = 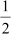 × base × height =
× base × height = 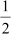 × 7 × 7 cm2 = 24.5 cm2
× 7 × 7 cm2 = 24.5 cm2
Thus, area of the segment PSR = area of the quadrant QPSR − area of ΔPQR
= (38.5 − 24.5) cm2
= 14 cm2
Therefore, area of the shaded portion = area of the semi-circle PTR − area of the
segment PSR
= (38.5 − 14) cm2
= 24.5 cm2
Example 3: In the following figure, the two mutually perpendicular diameters PQ and RS of the circle meet at centre O. Another circle is drawn through R and O. If the area of the shaded portion is 266 cm2, then find the radius of the circle.
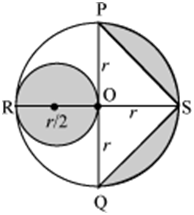
Solution:
Let the radius of original circle = r = OS = OP = OQ = OR
Radius of the circle through R and O =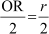
As PQ and RS are perpendicular to each other, therefore, OS is the height of the triangle PSQ.
It can be clearly noticed from the figure that
Area of shaded portion = Area of circle through R and O + Area of semi-circle PSQ − Area of Δ PSQ
266 =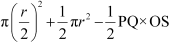
266 =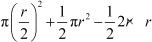
266 =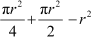
266 =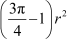
266 =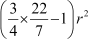
266 =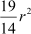
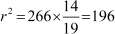
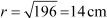
Hence, the radius of the circle is 14 cm.

 ACERISE INDIA
ACERISE INDIA
 SonikaAnandAcademy
SonikaAnandAcademy
