1.Euclid's division lemma
- Books Name
- Mathematics Book for CBSE Class 10
- Publication
- Carrier Point
- Course
- CBSE Class 10
- Subject
- Mathmatics
Euclid’s Division Lemma
Consider the following folk puzzle.
A trader was moving along a road selling eggs. An idler who didn’t have
much work to do, started to get the trader into a wordy duel. This grew into a
fight, he pulled the basket with eggs and dashed it on the floor. The eggs broke.
The trader requested the Panchayat to ask the idler to pay for the broken eggs.
The Panchayat asked the trader how many eggs were broken. He gave the
following response:
If counted in pairs, one will remain;
If counted in threes, two will remain;
If counted in fours, three will remain;
If counted in fives, four will remain;
If counted in sixes, five will remain;
If counted in sevens, nothing will remain;
My basket cannot accommodate more than 150 eggs.
So, how many eggs were there? Let us try and solve the puzzle. Let the number
of eggs be a. Then working backwards, we see that a is less than or equal to 150:
If counted in sevens, nothing will remain, which translates to a = 7p + 0, for
some natural number p. If counted in sixes, a = 6q+5, for some natural number q.
If counted in fives, four will remain. It translates to a = 5w + 4, for some natural
number w.
If counted in fours, three will remain. It translates to a = 4s + 3, for some natural
number s.
If counted in threes, two will remain. It translates to a = 3t + 2, for some natural
number t.
If counted in pairs, one will remain. It translates to a = 2u + 1, for some natural
number u.
That is, in each case, we have a and a positive integer b (in our example,
b takes values 7, 6, 5, 4, 3 and 2, respectively) which divides a and leaves a remainder
r (in our case, r is 0, 5, 4, 3, 2 and 1, respectively), that is smaller than b. The
* This is modified form of a puzzle given in ‘Numeracy Counts!’ by A. Rampal, and others. moment we write down such equations we are using Euclid’s division lemma,
which is given in Theorem 1.1.
Getting back to our puzzle, do you have any idea how you will solve it? Yes! You
must look for the multiples of 7 which satisfy all the conditions. By trial and error
(using the concept of LCM), you will find he had 119 eggs.
In order to get a feel for what Euclid’s division lemma is, consider the following
pairs of integers:
17, 6; 5, 12; 20, 4
Like we did in the example, we can write the following relations for each such
pair:
17 = 6 × 2 + 5 (6 goes into 17 twice and leaves a remainder 5)
5 = 12 × 0 + 5 (This relation holds since 12 is larger than 5)
20 = 4 × 5 + 0 (Here 4 goes into 20 five-times and leaves no remainder)
That is, for each pair of positive integers a and b, we have found whole numbers
q and r, satisfying the relation:
a = bq + r, 0 £ r < b
Note that q or r can also be zero.
Why don’t you now try finding integers q and r for the following pairs of positive
integers a and b?
(i) 10, 3; (ii) 4, 19; (iii) 81, 3
Did you notice that q and r are unique? These are the only integers satisfying the
conditions a = bq + r, where 0 £ r < b. You may have also realised that this is nothing
but a restatement of the long division process you have been doing all these years, and
that the integers q and r are called the quotient and remainder, respectively.
A formal statement of this result is as follows:
Theorem 1.1 (Euclid’s Division Lemma): Given positive integers a and b,
there exist unique integers q and r satisfying a = bq + r, 0 £ r < b.
This result was perhaps known for a long time, but was first recorded in Book VII
of Euclid’s Elements. Euclid’s division algorithm is based on this lemma.

Euclid’s division algorithm is a technique to compute the Highest Common Factor
(HCF) of two given positive integers. Recall that the HCF of two positive integers a
and b is the largest positive integer d that divides both a and b.
Let us see how the algorithm works, through an example first. Suppose we need
to find the HCF of the integers 455 and 42. We start with the larger integer, that is,
455. Then we use Euclid’s lemma to get
455 = 42 × 10 + 35
Now consider the divisor 42 and the remainder 35, and apply the division lemma
to get
42 = 35 × 1 + 7
Now consider the divisor 35 and the remainder 7, and apply the division lemma
to get
35 = 7 × 5 + 0
Notice that the remainder has become zero, and we cannot proceed any further.
We claim that the HCF of 455 and 42 is the divisor at this stage, i.e., 7. You can easily
verify this by listing all the factors of 455 and 42. Why does this method work? It
works because of the following result.
So, let us state Euclid’s division algorithm clearly.
To obtain the HCF of two positive integers, say c and d, with c > d, follow
the steps below:
Step 1: Apply Euclid’s division lemma, to c and d. So, we find whole numbers, q and
r such that c = dq + r, 0 £ r < d.
Step 2: If r = 0, d is the HCF of c and d. If r ¹ 0, apply the division lemma to d and r.
Step 3: Continue the process till the remainder is zero. The divisor at this stage will be the required HCF.
This algorithm works because HCF (c, d) = HCF (d, r) where the symbol
HCF (c, d) denotes the HCF of c and d, etc.
Example 1: Use Euclid’s algorithm to find the HCF of 4052 and 12576.
Solution:
Step 1: Since 12576 > 4052, we apply the division lemma to 12576 and 4052, to get
12576 = 4052 × 3 + 420
Step 2: Since the remainder 420 ¹ 0, we apply the division lemma to 4052 and 420, to
get
4052 = 420 × 9 + 272
Step 3: We consider the new divisor 420 and the new remainder 272, and apply the division lemma to get
420 = 272 × 1 + 148
We consider the new divisor 272 and the new remainder 148, and apply the division lemma to get
272 = 148 × 1 + 124
We consider the new divisor 148 and the new remainder 124, and apply the division lemma to get
148 = 124 × 1 + 24
We consider the new divisor 124 and the new remainder 24, and apply the division lemma to get
124 = 24 × 5 + 4
We consider the new divisor 24 and the new remainder 4, and apply the division lemma to get
24 = 4 × 6 + 0
The remainder has now become zero, so our procedure stops. Since the divisor at this stage is 4, the HCF of 12576 and 4052 is 4.
Notice that 4 = HCF (24, 4) = HCF (124, 24) = HCF (148, 124) =
HCF (272, 148) = HCF (420, 272) = HCF (4052, 420) = HCF (12576, 4052).
Euclid’s division algorithm is not only useful for calculating the HCF of very
large numbers, but also because it is one of the earliest examples of an algorithm that
a computer had been programmed to carry out.
Remarks:
1. Euclid’s division lemma and algorithm are so closely interlinked that people often
call former as the division algorithm also.
2. Although Euclid’s Division Algorithm is stated for only positive integers, it can be
extended for all integers except zero, i.e., b ¹ 0. However, we shall not discuss this
aspect here.
Euclid’s division lemma/algorithm has several applications related to finding
properties of numbers. We give some examples of these applications below:
Example 2: Show that every positive even integer is of the form 2q, and that every
positive odd integer is of the form 2q + 1, where q is some integer.
Solution: Let a be any positive integer and b = 2. Then, by Euclid’s algorithm,
a = 2q + r, for some integer q ³ 0, and r = 0 or r = 1, because 0 £ r < 2. So,
a = 2q or 2q + 1.
If a is of the form 2q, then a is an even integer. Also, a positive integer can be
either even or odd. Therefore, any positive odd integer is of the form 2q + 1.
Example 3: Show that any positive odd integer is of the form 4q + 1 or 4q + 3, where
q is some integer.
Solution: Let us start with taking a, where a is a positive odd integer. We apply the
division algorithm with a and b = 4.
Since 0 £ r < 4, the possible remainders are 0, 1, 2 and 3.
That is, a can be 4q, or 4q + 1, or 4q + 2, or 4q + 3, where q is the quotient.
However, since a is odd, a cannot be 4q or 4q + 2 (since they are both divisible by 2).
Therefore, any odd integer is of the form 4q + 1 or 4q + 3.
Example 4: A sweet seller has 420 kaju barfis and 130 badam barfis. She wants to
stack them in such a way that each stack has the same number, and they take up the
least area of the tray. What is the number of that can be placed in each stack for this purpose?
Solution: This can be done by trial and error. But to do it systematically, we find
HCF (420, 130). Then this number will give the maximum number of barfis in each
stack and the number of stacks will then be the least. The area of the tray that is used
up will be the least.
Now, let us use Euclid’s algorithm to find their HCF. We have:
420 = 130 × 3 + 30
130 = 30 × 4 + 10
30 = 10 × 3 + 0
So, the HCF of 420 and 130 is 10.
Therefore, the sweet seller can make stacks of 10 for both kinds of barfi.
1.Euclid's division lemma
- Books Name
- Mr. Sudhanshu Sharma Mathematics Book
- Publication
- Success Academy
- Course
- CBSE Class 10
- Subject
- Mathmatics

1.Euclid's division lemma
Euclid's Division Lemma: An Introduction
According to Euclid’s Division Lemma if we have two positive integers a and b, then there exist unique integers q and r which satisfies the condition a = bq + r where 0 ≤ r < b.
The basis of the Euclidean division algorithm is Euclid’s division lemma. To calculate the Highest Common Factor (HCF) of two positive integers a and b we use Euclid’s division algorithm. HCF is the largest number which exactly divides two or more positive integers. That means, on dividing both the integers a and b the remainder is zero.

Let us now get into the working of this Euclidean algorithm.
Euclid’s Division Lemma Algorithm
Consider two numbers 78 and 980 and we need to find the HCF of these numbers. To do this, we choose the largest integer first, i.e. 980 and then according to Euclid Division Lemma, a = bq + r where 0 ≤ r < b;
980 = 78 × 12 + 44
Now, here a = 980, b = 78, q = 12 and r = 44.
Now consider the divisor 78 and the remainder 44, apply Euclid division lemma again.
78 = 44 × 1 + 34
Similarly, consider the divisor 44 and the remainder 34, apply Euclid division lemma to 44 and 34.
44 = 34 × 1 + 10
Following the same procedure again,
34 = 10 × 3 + 4
10 = 4 × 2 + 2
4 = 2 × 2 + 0
As we see that the remainder has become zero, therefore, proceeding further is not possible. Hence, the HCF is the divisor b left in the last step. We can conclude that the HCF of 980 and 78 is 2.
Let us try another example to find the HCF of two numbers 250 and 75. Here, the larger the integer is 250, therefore, by applying Euclid Division Lemma a = bq + r where 0 ≤ r < b, we have
a = 250 and b = 75
⇒ 250 = 75 × 3 + 25
By applying the Euclid’s Division Algorithm to 75 and 25, we have:
75 = 25 × 3 + 0
As the remainder becomes zero, we cannot proceed further. According to the algorithm, in this case, the divisor is 25. Hence, the HCF of 250 and 75 is 25.
Example
Example: Find the HCF of 81 and 675 using the Euclidean division algorithm.
Solution: The larger integer is 675, therefore, by applying the Division Lemma a = bq + r where 0 ≤ r < b, we have
a = 675 and b = 81
⇒ 675 = 81 × 8 + 27
By applying Euclid’s Division Algorithm again we have,
81 = 27 × 3 + 0
We cannot proceed further as the remainder becomes zero. According to the algorithm, in this case, the divisor is 27. Hence, the HCF of 675 and 81 is 27.
This algorithm has got many practical applications in finding the properties of numbers. There is a lot more left to learn in real numbers. Enrich your knowledge by visiting our website www.byjus.com and download BYJU’S-the learning app and learn anywhere.
1.Euclid's division lemma
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics


1.Euclid's division lemma
Chapter 1: Real Numbers
Euclids Division Lemma
What is a dividend? Let us understand it with the help of a simple example. Can you divide 14 by 6?
![]()
After division, we get 2 as the quotient and 2 as the remainder.
Thus, we can also write 14 as 6 × 2 + 2.
A dividend can thus be written as:
Dividend = Divisor × Quotient + Remainder
Can you think of any other number which, when multiplied with 6, gives 14 as the dividend and 2 as the remainder?
Let us try it out with some other sets of dividends and divisors.
(1) Divide 100 by 20: 100 = 20 × 5 + 0
(2) Divide 117 by 15: 117 = 15 × 7 + 12
(3) Divide 67 by 17: 67 = 17 × 3 + 16
Thus, if we have a dividend and a divisor, then there will be a unique pair of a quotient and a remainder that will fit into the above equation.
This brings us to Euclid’s division lemma.
If a and b are positive integers, then there exist two unique integers, q and r,
such that a = bq + r
This lemma is very useful for finding the H.C.F. of large numbers where breaking them into factors is difficult. This method is known as Euclid’s Division Algorithm.
Let us look at some more examples.
Example 1: Find the H.C.F. of 4032 and 262 using Euclid’s division algorithm.
Solution:
Step 1:
First, apply Euclid’s division lemma on 4032 and 262.
4032 = 262 × 15 + 102
Step 2:
As the remainder is non-zero, we apply Euclid’s division lemma on 262 and 102.
262 = 102 × 2 + 58
Step 3:
Apply Euclid’s division lemma on 102 and 58.
102 = 58 × 1 + 44
Step 4:
Apply Euclid’s division lemma on 58 and 44.
58 = 44 × 1 + 14
Step 5:
Apply Euclid’s division lemma on 44 and 14.
44 = 14 × 3 + 2
Step 6:
Apply Euclid’s division lemma on 14 and 2.
14 = 2 × 7 + 0
In the problem given above, to obtain 0 as the remainder, the divisor has to be taken as 2. Hence, 2 is the H.C.F. of 4032 and 262.
Note that Euclid’s division algorithm can be applied to polynomials also.
Example 2: A rectangular garden of dimensions 190 m × 60 m is to be divided in square blocks to plant different flowers in each block. Into how many blocks can this garden be divided so that no land is wasted?
Solution:
If we do not want to waste any land, we need to find the largest number that completely divides both 190 and 60 and gives the remainder 0, i.e., the H.C.F. of (190, 60).
To find the H.C.F., let us apply Euclid’s algorithm.
190 = 60 × 3 + 10
60 = 10 × 6 + 0
Therefore, the H.C.F. of 190 and 60 is 10.
Therefore, there will be![]()
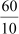
Hence, the total number of blocks in the garden will be 19 × 6 = 114.
Example 3: Find the H.C.F. of 336 and 90 using Euclid’s division algorithm.
Solution:
As 336 > 90, we apply the division lemma to 336 and 90.
336 = 90 × 3 + 66
Applying Euclid’s division lemma to 90 and 66: 90 = 66 × 1 + 24
Applying Euclid’s division lemma to 66 and 24:
66 = 24 × 2 + 18
Applying Euclid’s division lemma to 24 and 18:
24 = 18 × 1 + 6
Applying Euclid’s division lemma to 18 and 6:
18 = 6 × 3 + 0
As the remainder is zero, we need not apply Euclid’s division lemma anymore. The divisor (6) is the required H.C.F.
Example 4: Find the H.C.F. of 45, 81, and 117 using Euclid’s division algorithm.
Solution:
Let us begin by choosing any two out of the three given numbers, say 45 and 81. As 81 > 45, we apply Euclid’s division lemma to 81 and 45.
81 = 45 × 1 + 36
Applying Euclid’s division lemma to 45 and 36:
45 = 36 × 1 + 9
Applying Euclid’s division lemma to 36 and 9:
36 = 9 × 4 + 0
As the remainder is zero, the H.C.F. of 45 and 81 is 9.
Now, we again need to apply Euclid’s division algorithm on the H.C.F. of the two numbers and the remaining number.
Since the H.C.F. of 45 and 81 is 9 and the third number is 117, we apply Euclid’s division lemma to 117 and 9.
117 = 9 × 13 + 0
As the remainder is zero, the H.C.F. of 9 and 117 is 9.
Here, the second H.C.F. (the H.C.F. of the H.C.F. of the first two numbers and the third number) is the H.C.F. of the three numbers.
Thus, we can say that the H.C.F. of the three numbers is 9.
Example 5: In an inter-school essay writing competition, the numbers of participants from schools A, B, and C are 20, 16, and 28 respectively. If the participants in each room are from the same school, then find the minimum number of rooms required such that each room has the same number of participants.
Solution:
If we need to find the minimum number of rooms, then we need to keep the maximum number of participants in each room i.e., we need to find the largest number that completely divides 20, 16, and 28.
Thus, we start by choosing any two out of the given three numbers, say 20 and 16. Applying Euclid’s division lemma to 20 and 16:
20 = 16 × 1 + 4
Applying Euclid’s division lemma to 16 and 4:
16 = 4 × 4 + 0
Hence, 4 is the H.C.F. of 20 and 16.
Applying Euclid’s division algorithm to 28 and 4:
28 = 4 × 7 + 0
Hence, 4 is the H.C.F. of 28 and 4.
∴H.C.F. of 20, 16, 28 = 4
Therefore, each room would have 4 participants.
The number of rooms in which the participants from schools A, B, and C can be
accommodated is 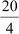
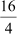
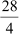
Therefore, a total of 5 + 4 + 7 =16 rooms are required.
The Use Of Euclids Division Lemma To Prove Mathematical Relationships
We can thus write this rule about the dividend as
This expression is unique, i.e., whenever we divide an integer (dividend) by another integer (divisor), we always get a fixed quotient and a fixed remainder.
The above statement can be proven by taking an example.
Whenever we divide 54 by 11, we will get 4 as the quotient and 10 as the remainder. We will never get a quotient other than 4 and a remainder other than 10 when we divide 54 by 11.
This brings us to Euclid’s division lemma.

This lemma has several applications, one of which is to prove mathematical relationships among numbers.
Let us discuss this concept with the help of a few examples.
Example 1: Prove that every positive integer is of the form 3p, 3p + 1, or 3p + 2, where p is any integer.
Solution:
Let a be any positive integer and let b = 3.
Applying Euclid’s algorithm to a and 3:
a = 3p + r; for some integer p and 0 ≤ r < 3
Therefore, a can be 3p, 3p + 1, or 3p + 2.
As a is a positive integer, we can say that any positive integer is of the form 3p, 3p + 1, or 3p + 2.
Example 2: Prove that every positive even integer is of the form 2m and every positive odd integer is of the form 2m + 1, where m is any integer.
Solution:
Let a be any positive integer and let b = 2.
According to Euclid’s division lemma, there exist two unique integers m and r such that
a = bm + r = 2m + r, where 0 ≤ r < 2. Thus, r = 0 or 1
If r = 0, i.e., if a = 2m, then the expression is divisible by 2. Thus, it is an even number.
If r = 1, i.e., if a = 2m + 1, then the expression is not divisible by 2. Thus, it is an odd number.
Thus, every positive even integer is of the form 2m and every positive odd integer is of the form 2m + 1.
Example 3: Prove that the expression y(y + 1) always represents an even number, where y is any positive integer.
Solution:
Let y be an integer. Thus, it may be either odd or even.
When y is an odd number, i.e., when y is of the form 2p + 1, where p is an integer:
y(y + 1) = (2p + 1)(2p + 1 + 1) = (2p + 1)(2p + 2) = 2(2p + 1)(p + 1)
The above expression is a multiple of 2. Thus, the expression y(y + 1) represents an even number.
When y is an even number, i.e., when y is of the form 2q, where q is an integer:
y(y + 1) = (2q)(2q + 1) = 2q(2q + 1)
The above expression is a multiple of 2. Thus, the expression y(y + 1) represents an even number.
Thus, for a positive integer y, the expression y(y + 1) always represents an even number.
Example 4:
Show that
(a) The sum, the difference, and the product of two even numbers is always even.
(b) The sum and the difference of two odd numbers is always even, whereas their product is always odd.
Solution:
(a) Let there be two even numbers, x and y, such that x = 2m and y = 2n, where m and n are two positive integers.
Now, x + y = 2m + 2n = 2(m + n) = 2p, where p = m + n is an integer. Thus, x + y is always even.
Similarly, x − y = 2m − 2n = 2(m − n) = 2q, where q = m − n is an integer. Thus, x − y is always even.
Likewise, xy = 2m × 2n = 4mn = 2(2mn) = 2t, where t = 2mn is an integer. Thus, xy is always even.
Hence, the sum, the difference, and the product of two even numbers is always even.
(b) Let there be two odd numbers x and y such that x = 2m + 1 and y = 2n + 1, where m and n are two positive integers.
Now, x + y = (2m + 1) + (2n + 1) = 2(m + n + 1) = 2p, where p = m + n + 1 is an integer. Thus, x + y is even.
Similarly, x − y = (2m + 1) − (2n + 1) = 2(m − n) = 2q, where q = m − n is an integer.
Thus, x − y is even.
Likewise, xy = (2m + 1)(2n + 1) = 2(2mn + m + n) + 1 = 2t + 1, where t = 2mn + m + n is an integer.
Thus, xy is always odd.
Hence, the sum and the difference of two odd numbers is always even, whereas their product is always odd.
1.Euclid's division lemma
- Books Name
- Sample paper Term II Maths
- Publication
- SonikaAnandAcademy
- Course
- CBSE Class 10
- Subject
- Mathmatics

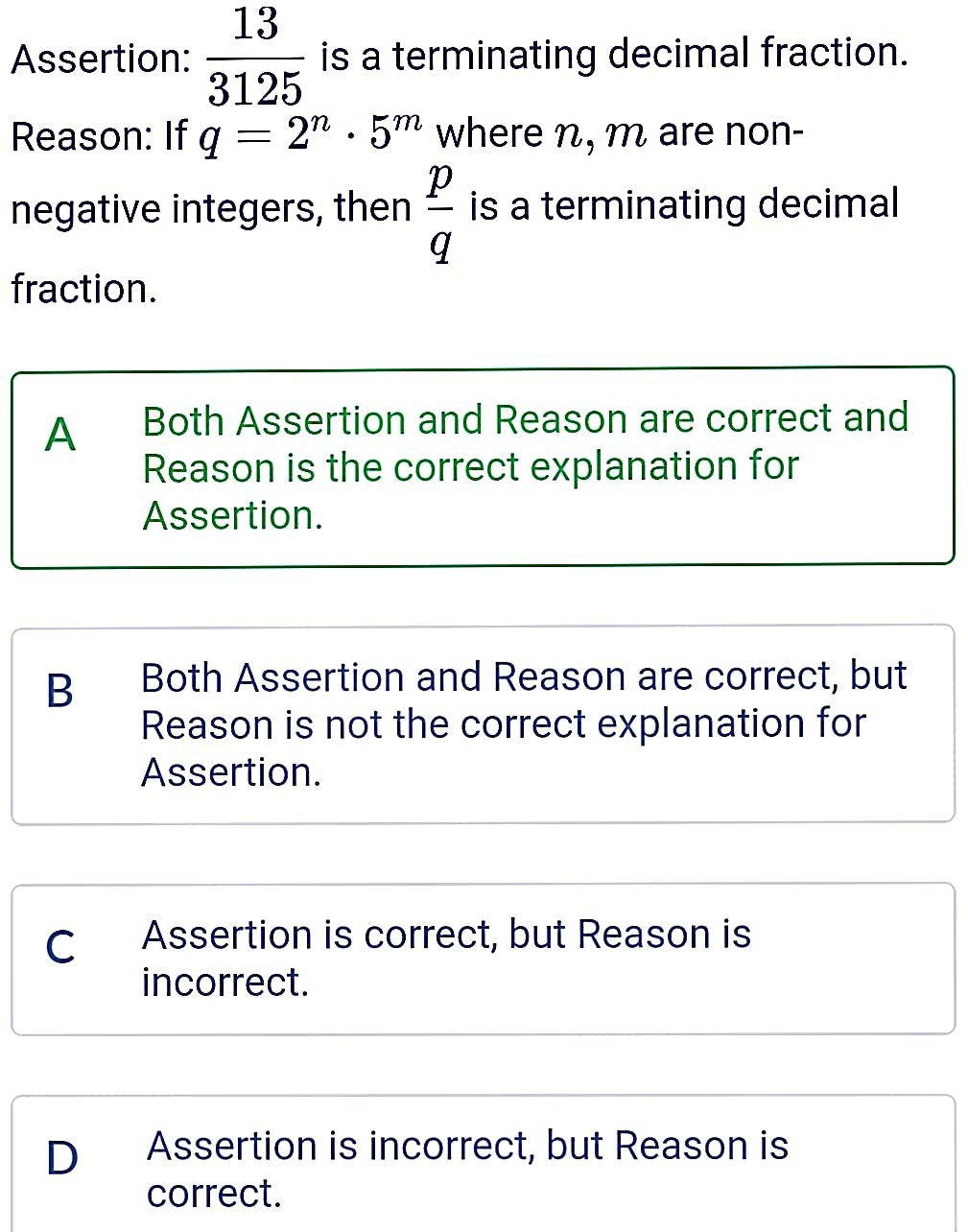

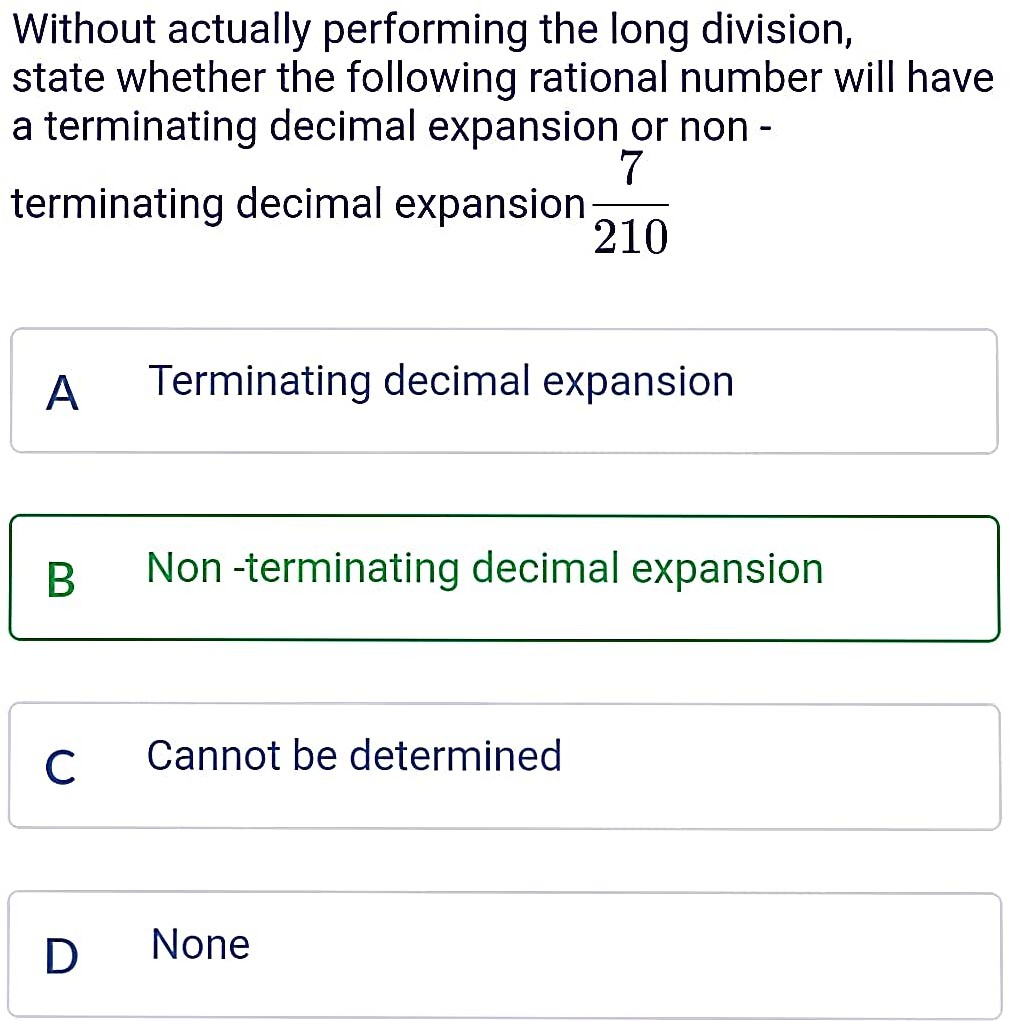







1.Euclid's division lemma
Sample
2.Arithmetic Fundamental Theorem
- Books Name
- Mathematics Book for CBSE Class 10
- Publication
- Carrier Point
- Course
- CBSE Class 10
- Subject
- Mathmatics
The Fundamental Theorem of Arithmetic
In your earlier classes, you have seen that any natural number can be written as a
product of its prime factors. For instance, 2 = 2, 4 = 2 × 2, 253 = 11 × 23, and so on.
Now, let us try and look at natural numbers from the other direction. That is, can any
natural number be obtained by multiplying prime numbers? Let us see.
Take any collection of prime numbers, say 2, 3, 7, 11 and 23. If we multiply
some or all of these numbers, allowing them to repeat as many times as we wish,
we can produce a large collection of positive integers (In fact, infinitely many).
Let us list a few:
7 × 11 × 23 = 1771 3 × 7 × 11 × 23 = 5313
2 × 3 × 7 × 11 × 23 = 10626 23 × 3 × 73 = 8232
22 × 3 × 7 × 11 × 23 = 21252
and so on.
Now, let us suppose your collection of primes includes all the possible primes.
What is your guess about the size of this collection? Does it contain only a finite
number of integers, or infinitely many? Infact, there are infinitely many primes. So, if
we combine all these primes in all possible ways, we will get an infinite collection of
numbers, all the primes and all possible products of primes. The question is – can we
produce all the composite numbers this way? What do you think? Do you think that
there may be a composite number which is not the product of powers of primes?
Before we answer this, let us factorise positive integers, that is, do the opposite of
what we have done so far.
We are going to use the factor tree with which you are all familiar. Let us take
some large number, say, 32760, and factorise it as shown:

So, we have factorised 32760 as 2 × 2 × 2 × 3 × 3 × 5 × 7 × 13 as a product of
primes, i.e., 32760 = 23 × 32 × 5 × 7 × 13 as a product of powers of primes. Let us try
another number, say, 123456789. This can be written as 32 × 3803 × 3607. Of course,
you have to check that 3803 and 3607 are primes! (Try it out for several other natural
numbers yourself.) This leads us to a conjecture that every composite number can be
written as the product of powers of primes. In fact, this statement is true, and is called the Fundamental Theorem of Arithmetic because of its basic crucial importance to the study of integers. Let us now formally state this theorem.
Theorem 1.2 (Fundamental Theorem of Arithmetic): Every composite number
can be expressed (factorised) as a product of primes, and this factorisation is
unique, apart from the order in which the prime factors occur.

The Fundamental Theorem of Arithmetic says that every composite number
can be factorised as a product of primes. Actually it says more. It says that given
any composite number it can be factorised as a product of prime numbers in a
‘unique’ way, except for the order in which the primes occur. That is, given any
composite number there is one and only one way to write it as a product of primes,
as long as we are not particular about the order in which the primes occur. So, for
example, we regard 2 × 3 × 5 × 7 as the same as 3 × 5 × 7 × 2, or any other
possible order in which these primes are written. This fact is also stated in the
following form:
The prime factorisation of a natural number is unique, except for the order
of its factors.
In general, given a composite number x, we factorise it as x = p1 p 2 ... pn, where
p1
, p2
,..., pn are primes and written in ascending order, i.e., p1
£ p2
£ . . . £ p
n
. If we combine the same primes, we will get powers of primes. For example,
32760 = 2 × 2 × 2 × 3 × 3 × 5 × 7 × 13 = 23 × 32 × 5 × 7 × 13
Once we have decided that the order will be ascending, then the way the number
is factorised, is unique.
The Fundamental Theorem of Arithmetic has many applications, both within
mathematics and in other fields. Let us look at some examples.
Example 5: Consider the numbers 4n, where n is a natural number. Check whether
there is any value of n for which 4n ends with the digit zero.
Solution: If the number 4n, for any n, were to end with the digit zero, then it would be divisible by 5. That is, the prime factorisation of 4n would contain the prime 5.
not possible because 4n = (2)2n; so the only prime in the factorisation of 4n is 2. So, the
uniqueness of the Fundamental Theorem of Arithmetic guarantees that there are no
other primes in the factorisation of 4n. So, there is no natural number n for which 4n
ends with the digit zero.
You have already learnt how to find the HCF and LCM of two positive integers
using the Fundamental Theorem of Arithmetic in earlier classes, without realising it!
This method is also called the prime factorisation method. Let us recall this method
through an example.
Example 6: Find the LCM and HCF of 6 and 20 by the prime factorisation method.
Solution: We have: 6 = 21 × 31 and 20 = 2 × 2 × 5 = 22 × 51.
You can find HCF (6, 20) = 2 and LCM (6, 20) = 2 × 2 × 3 × 5 = 60, as done in your
earlier classes.
Note that HCF (6, 20) = 21 = Product of the smallest power of each common
prime factor in the numbers.
LCM (6, 20) = 22 × 31 × 51 = Product of the greatest power of each prime factor, involved in the numbers.
From the example above, you might have noticed that HCF (6, 20) × LCM (6, 20)
= 6 × 20. In fact, we can verify that for any two positive integers a and b,
HCF (a, b) × LCM (a, b) = a × b. We can use this result to find the LCM of two
positive integers, if we have already found the HCF of the two positive integers.
Example 7: Find the HCF of 96 and 404 by the prime factorisation method. Hence,
find their LCM.
Solution: The prime factorisation of 96 and 404 gives:
96 = 25 × 3, 404 = 22 × 101
Therefore, the HCF of these two integers is 22 = 4.
Also, LCM (96, 404) =
96 404 96 404
9696
HCF (96, 404) 4
Example 8: Find the HCF and LCM of 6, 72 and 120, using the prime factorisation
method.
Solution: We have:
6 = 2 × 3, 72 = 23 × 32, 120 = 23 × 3 × 5
Here, 21 and 31 are the smallest powers of the common factors 2 and 3, respectively.
So, HCF (6, 72, 120) = 21 × 31 = 2 × 3 = 6
23, 32 and 51 are the greatest powers of the prime factors 2, 3 and 5 respectively
involved in the three numbers.
So, LCM (6, 72, 120) = 23 × 32 × 51 = 360
Remark: Notice, 6 × 72 × 120 ¹ HCF (6, 72, 120) × LCM (6, 72, 120). So, the
product of three numbers is not equal to the product of their HCF and LCM.
2.Arithmetic Fundamental Theorem
- Books Name
- Mr. Sudhanshu Sharma Mathematics Book
- Publication
- Success Academy
- Course
- CBSE Class 10
- Subject
- Mathmatics
|
Subject |
Unit |
Chapter |
Day |
Maximum Marks: |
|||
|
Zoology |
Chemical Coordination and Integration |
1 |
Negative Marks: |
||||
|
Type of Question:- |
Single Choice |
Multiple |
Integer |
||||
|
Source:- |
|||||||
|
Information:- |
Single Choice |
||||||
|
Question:- 107 |
I. ACTH II. GH III. MSH IV. FSH V. LH VI. Oxytocin Which of the above hormones are polypeptide or proteinaceous in nature? Choose the correct option. |
||||||
|
Hint :- |
|||||||
|
Conceptual |
Easy |
Medium |
Difficult |
||||
|
IITJEE |
AIEEE |
BITS |
Regional |
Board |
NCERT |
||
|
Solution:- |
I, II, III and IV. Refer to Ans. No. 83. |
||||||
|
Is Correct |
|||||||
|
Option 1 |
I, II, III and IV |
||||||
|
Option 2 |
III, IV, V and VI |
||||||
|
Option 3 |
III, IV, V and VI |
||||||
|
Option 4 |
I, II, III and VI |
* |
|||||
|
Subject |
Unit |
Chapter |
Day |
Maximum Marks: |
|||||||||||||
|
Zoology |
Chemical Coordination and Integration |
1 |
Negative Marks: |
||||||||||||||
|
Type of Question:- |
Single Choice |
Multiple |
Integer |
||||||||||||||
|
Source:- |
|||||||||||||||||
|
Information:- |
Single Choice |
||||||||||||||||
|
Question:- 140 |
Match the following columns.
Codes A B C D |
||||||||||||||||
|
Hint :- |
|||||||||||||||||
|
Conceptual |
Easy |
Medium |
Difficult |
||||||||||||||
|
IITJEE |
AIEEE |
BITS |
Regional |
Board |
NCERT |
||||||||||||
|
Solution:- |
On the basis of nature, hormones can be divided into four groups (i) peptide, polypeptide , protein hormone (e.g.,) Insulin, glucagon, pituitary hormones, hypothalamic hormones). (ii) Sterols (e.g, Cortisol, testosterone, estradiol and progesterone). (iii) lodothyronine (e.g., Thyroid hormones). (iv) Amino acid derivaties (e.g., Epinephrine). |
||||||||||||||||
|
Is Correct |
|||||||||||||||||
|
Option 1 |
1 2 3 4 |
||||||||||||||||
|
Option 2 |
4 3 2 1 |
||||||||||||||||
|
Option 3 |
4 2 3 1 |
* |
|||||||||||||||
|
Option 4 |
4 2 1 3 |
||||||||||||||||
|
Subject |
Unit |
Chapter |
Day |
Maximum Marks: |
|||||||||||||||||
|
Zoology |
Chemical Coordination and Integration |
1 |
Negative Marks: |
||||||||||||||||||
|
Type of Question:- |
Single Choice |
Multiple |
Integer |
||||||||||||||||||
|
Source:- |
|||||||||||||||||||||
|
Information:- |
Single Choice |
||||||||||||||||||||
|
Question:- 167 |
Match the following columns and choose the correct option from the codes given below
Codes |
||||||||||||||||||||
|
Hint :- |
|||||||||||||||||||||
|
Conceptual |
Easy |
Medium |
Difficult |
||||||||||||||||||
|
IITJEE |
AIEEE |
BITS |
Regional |
Board |
NCERT |
||||||||||||||||
|
Solution:- |
Exocrine gland Liver and gastric gland Endocrine gland Thyroid and adrenal gland Heterocrine gland Ovary and testis. |
||||||||||||||||||||
|
Is Correct |
|||||||||||||||||||||
|
Option 1 |
A- 1, 2; B-3, 4; C-5, 6 |
* |
|||||||||||||||||||
|
Option 2 |
A- 1, 2, 3; B-4, 5; C-6 |
||||||||||||||||||||
|
Option 3 |
A- 1; B-2, 3,4; C-5, 6 |
||||||||||||||||||||
|
Option 4 |
A- 1; B-2, 3; C-4,5, 6 |
||||||||||||||||||||
|
Subject |
Unit |
Chapter |
Day |
Maximum Marks: |
|||
|
Zoology |
Chemical Coordination and Integration |
1 |
Negative Marks: |
||||
|
Type of Question:- |
Single Choice |
Multiple |
Integer |
||||
|
Source:- |
|||||||
|
Information:- |
Single Choice |
||||||
|
Question:- 192 |
Tyrosine is the precursor of |
||||||
|
Hint :- |
|||||||
|
Conceptual |
Easy |
Medium |
Difficult |
||||
|
IITJEE |
AIEEE |
BITS |
Regional |
Board |
NCERT |
||
|
Solution:- |
The conversion of tyrosine to epinephrine involves four steps (i) Ring hydroxylation (ii) Decarboxylation (iii) Side chain hydroxylation (iv) N-methylation Tyrosine Tyrosine hydroxylase (Dihydroxyphenylalanine) Dopa-decarboxylase Dopamine Dopamine--Hydroxylase Norepinephrine PNMT (Phenyl ethanolamine-N-methyl transferase). Epinephrine |
||||||
|
Is Correct |
|||||||
|
Option 1 |
Epinephrine |
||||||
|
Option 2 |
Norepinephrine |
||||||
|
Option 3 |
Testosterone |
||||||
|
Option 4 |
Both (a) and (b) |
* |
|||||
|
Subject |
Unit |
Chapter |
Day |
Maximum Marks: |
|||
|
Zoology |
Chemical Coordination and Integration |
1 |
Negative Marks: |
||||
|
Type of Question:- |
Single Choice |
Multiple |
Integer |
||||
|
Source:- |
|||||||
|
Information:- |
Single Choice |
||||||
|
Question:- 203 |
Endocrine glands are the glands which |
||||||
|
Hint :- |
|||||||
|
Conceptual |
Easy |
Medium |
Difficult |
||||
|
IITJEE |
AIEEE |
BITS |
Regional |
Board |
NCERT |
||
|
Solution:- |
Endocrine system is a system of isolated glands that pour their secretion directly into venous blood or lymph for passage to different body organs in order to control their functioning. Metabolism, cell permeability, growth differentiation and stress condition. |
||||||
|
Is Correct |
|||||||
|
Option 1 |
Pour their secretions directly into blood |
* |
|||||
|
Option 2 |
Pour their secretions indirectly into blood |
||||||
|
Option 3 |
Have ducts |
||||||
|
Option 4 |
All of the above |
||||||
|
Subject |
Unit |
Chapter |
Day |
Maximum Marks: |
|||
|
Zoology |
Chemical Coordination and Integration |
1 |
Negative Marks: |
||||
|
Type of Question:- |
Single Choice |
Multiple |
Integer |
||||
|
Source:- |
|||||||
|
Information:- |
Single Choice |
||||||
|
Question:- 205 |
Reproductive glands are also called |
||||||
|
Hint :- |
|||||||
|
Conceptual |
Easy |
Medium |
Difficult |
||||
|
IITJEE |
AIEEE |
BITS |
Regional |
Board |
NCERT |
||
|
Solution:- |
Types of glands on the basis of presence or absence of ducts. (i) Exocrine Gland Those which drain out their secretion through duct. Live, gastric glands, etc. (ii) Endocrine Gland Those gland which lack duct and discharge their secretion (hormones) directly into the blood stream. Due to absence of duct they are also called, ductless gland or Holocrine glands, e.g. thyroid, parathyroid, pituitary gland. (iii) Heterocrine Gland Those gland which have dual function due to possession of both exocrine as well as endocrine region. They secrete hormone in association with other substances for their respective function ovary, testes, pancreas. |
||||||
|
Is Correct |
|||||||
|
Option 1 |
Exocrine glands |
||||||
|
Option 2 |
Holocrine glands |
||||||
|
Option 3 |
Heterocrine glands |
* |
|||||
|
Option 4 |
Enzyme secreting glands |
||||||
|
Subject |
Unit |
Chapter |
Day |
Maximum Marks: |
|||
|
Zoology |
Chemical Coordination and Integration |
1 |
Negative Marks: |
||||
|
Type of Question:- |
Single Choice |
Multiple |
Integer |
||||
|
Source:- |
|||||||
|
Information:- |
Single Choice |
||||||
|
Question:- 96 |
Which of the following are Heterocrine glands. I. Thyroid II. Parathyroid III. Ovary IV. Testis V. Pituitary VI. Pancreas Choose the correct option. |
||||||
|
Hint :- |
|||||||
|
Conceptual |
Easy |
Medium |
Difficult |
||||
|
IITJEE |
AIEEE |
BITS |
Regional |
Board |
NCERT |
||
|
Solution:- |
Glands which have dual function due to possession of both exocrine as well as endocrine region are called Heterocrine glands. They secrete hormone in association with other substances for their respective function, e.g. ovaries, testes and pancreas. |
||||||
|
Is Correct |
|||||||
|
Option 1 |
I, II and III |
||||||
|
Option 2 |
III, IV and VI |
* |
|||||
|
Option 3 |
I, V and VI |
||||||
|
Option 4 |
I, IV and V |
||||||
|
Subject |
Unit |
Chapter |
Day |
Maximum Marks: |
|||
|
Zoology |
Chemical Coordination and Integration |
1 |
Negative Marks: |
||||
|
Type of Question:- |
Single Choice |
Multiple |
Integer |
||||
|
Source:- |
|||||||
|
Information:- |
Single Choice |
||||||
|
Question:- 100 |
I. Pancreas II. Testis III. Liver IV. Thyroid gland V. Adrenal gland VI. Pituitary gland Which of the above given glands are endocrine glands? |
||||||
|
Hint :- |
|||||||
|
Conceptual |
Easy |
Medium |
Difficult |
||||
|
IITJEE |
AIEEE |
BITS |
Regional |
Board |
NCERT |
||
|
Solution:- |
(i) Liver is the exocrine (gland which drains out their secretion through duct). (ii) Pancreas, testis and ovary are the Heterocrine gland. (iii) Thymus, adrenal and pituitary, thyroid are the endocrine gland. |
||||||
|
Is Correct |
|||||||
|
Option 1 |
I and II |
||||||
|
Option 2 |
Only III |
||||||
|
Option 3 |
Only VI |
||||||
|
Option 4 |
IV, V and VI |
* |
|||||
|
Subject |
Unit |
Chapter |
Day |
Maximum Marks: |
|||||||||||
|
Zoology |
Chemical Coordination and Integration |
1 |
Negative Marks: |
||||||||||||
|
Type of Question:- |
Single Choice |
Multiple |
Integer |
||||||||||||
|
Source:- |
|||||||||||||||
|
Information:- |
Single Choice |
||||||||||||||
|
Question:- 169 |
Match the following columns.
Codes A B C |
||||||||||||||
|
Hint :- |
|||||||||||||||
|
Conceptual |
Easy |
Medium |
Difficult |
||||||||||||
|
IITJEE |
AIEEE |
BITS |
Regional |
Board |
NCERT |
||||||||||
|
Solution:- |
Types of hormone action are (i) Endocrine Action The action in which hormone is distributed in blood and binds to distant target cells. (ii) Paracrine Action The action in hormone acts locally by diffusing from its source to target cells in the neighborhood. e.g., cytokines. (iii) Autocrine Action The action in which hormone acts on the same cell that produced it. |
||||||||||||||
|
Is Correct |
|||||||||||||||
|
Option 1 |
1 2 3 |
||||||||||||||
|
Option 2 |
3 2 1 |
||||||||||||||
|
Option 3 |
2 3 1 |
* |
|||||||||||||
|
Option 4 |
2 1 3 |
||||||||||||||
2.Arithmetic Fundamental Theorem
Fundamental Theorem Of Arithmetic
Fundamental Theorem of Arithmetic states that every integer greater than 1 is either a prime number or can be expressed in the form of primes. In other words, all the natural numbers can be expressed in the form of the product of its prime factors. To recall, prime factors are the numbers which are divisible by 1 and itself only. For example, the number 35 can be written in the form of its prime factors as:
35 = 7 × 5
Here, 7 and 5 are the prime factors of 35
Similarly, another number 114560 can be represented as the product of its prime factors by using prime factorization method,
114560 = 27 × 5 × 179
So, we have factorized 114560 as the product of the power of its primes.
Therefore, every natural number can be expressed in the form of the product of the power of its primes. This statement is known as the Fundamental Theorem of Arithmetic, unique factorization theorem or the unique-prime-factorization theorem.

Proof for Fundamental Theorem of Arithmetic
In number theory, a composite number is expressed in the form of the product of primes and this factorization is unique apart from the order in which the prime factor occurs.
From this theorem we can also see that not only a composite number can be factorized as the product of their primes but also for each composite number the factorization is unique, not taking into consideration order of occurrence of the prime factors.
In simple words, there exists only a single way to represent a natural number by the product of prime factors. This fact can also be stated as:
The prime factorization of any natural number is said to be unique for except the order of their factors.
In general, a composite number “a” can be expressed as,
a = p1 p2 p3 ………… pn, where p1, p2, p3 ………… pn are the prime factors of a written in ascending order i.e. p1≤p2≤p3 ………… ≤pn.
Writing the primes in ascending order makes the factorization unique in nature.
Fundamental Theorem of Arithmetic Examples
Example Question: In a formula racing competition the time taken by two racing cars A and B to complete 1 round of the track is 30 minutes and 45 minutes respectively. After how much time will the cars meet again at the starting point?
Solution:
As the time taken by car B is more compared to that of A to complete one round therefore it can be assumed that A will reach early and both the cars will meet again when A has already reached the starting point. This time can be calculated by finding the L.C.M of the time taken by each.
30 = 2 × 3 × 5
45 = 3 × 3 × 5
The L.C.M is 90.
Thus, both cars will meet at the starting point after 90 minutes.
2.Arithmetic Fundamental Theorem
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
1.14 the Fundamental theorem of arithmetic :
heorem (Fundamental Theorem of Arithmetic) :
Every composite number can be expressed (factorised) as a product of primes and this factorisation is unique, apart from the order in which the prime factors occurs.
The prime factorisation of a natural number is unique except the order of its factors.


2.Arithmetic Fundamental Theorem
Prime Factorisation of Numbers Using Fundamental Theorem of Arithmetic
We know that all composite numbers can be represented as the product of two or more prime numbers. Let us understand this concept by taking the example of 36 and factorising it in different ways.
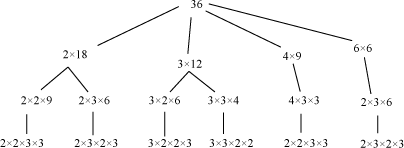
We can see that whichever way we factorise the number 36, it will be broken down as the product of the same prime numbers, which is unique. The only difference is that the ordering of the prime numbers will be different for different ways of factorising the number. In fact, this is true for all numbers. We can check this by taking the example of a larger number, say 21560, which can be uniquely broken down into its prime factors as
23 × 5 × 72 × 11
Hence, we can say that any composite number can be written in the form of the product of prime numbers, which is unique, except the order in which they occur. By this, we mean that 2 × 3 × 7 × 11 is the same as 7 × 11 × 2 × 3.
This is the fundamental theorem of arithmetic. It can be formally stated as:

Thus, this theorem can be used to write the prime factorisation of any number. Let us try to build on this concept with the help of some examples.
Example 1:
Write the prime factorization of 31250. What are its prime factors? Solution:
31250 = 2 × 15625
= 2 × 5 × 3125
= 2 × 5 × 5 × 625
= 2 × 5 × 5 × 5 × 125
= 2 × 5 × 5 × 5 × 5 × 25
= 2 × 5 × 5 × 5 × 5 × 5 × 5
= 2 × 56
Hence, 2 × 56 is the prime factorisation of 31250. Its prime factors are 2 and 5.
Example 2: If it is given that 13125 = 2a ×3b× 5c× 7d, then find the value of a +2b +7c + 11d.
Solution:
2a × 3b × 5c × 7d = 13125
= 3 × 4375
= 3 × 5 × 875
= 3 × 5 × 5 ×175
= 3 × 5 × 5 × 5 × 35
= 3 × 5 × 5 × 5 × 5 × 7
= 31 × 54 × 71
∴ 2a × 3b × 5c × 7d = 20 × 31 × 54 × 71
Comparing exponents of the bases (integers): a = 0, b = 1, c = 4, and d =1
Hence, a +2b +7c +11d = 0 + 2 ×1 + 7 × 4 + 11 × 1
= 0 + 2 + 28 + 11
= 41
Example 3: Show that the expressions given below are composite numbers.
(a) 3 × 5 × 7 × 23 + 2 × 7 × 11 × 13
(b) 29 × 35 + 14
(c) 34 + 63
Solution:
(a) 3 × 5 × 7 × 23 + 2 × 7 × 11 × 13 = 7( 3 × 5 × 23 + 2 × 11 × 13)
= 7(345 + 286)
= 7 × 631
Since both 7 and 631 are prime numbers, we have expressed the given expression as the product of two prime numbers. We know that according to the fundamental theorem of arithmetic, every composite number can be uniquely written as the product of its prime factors. Thus, the given expression represents a composite number.
(b) 29 × 35 + 14 = 29 × 5 × 7 + 2 × 7
= 7(29 × 5 + 2)
= 7 × 147
= 7 × 3 × 7 × 7
= 3 × 73
Since both 3 and 7 are prime numbers, we have expressed the given expression as the product of its prime factors. We know that according to the fundamental theorem of arithmetic, every composite number can be uniquely written as the product of its prime factors. Thus, the given expression represents a composite number.
(c) 34 + 63 = 34 + (2 × 3) 3
= 34 + 23 × 33
= 33(3 + 23)
= 33 × 11
Since both 3 and 11 are prime numbers, we have expressed the given expression as the product of its prime factors. It is known that according to the fundamental theorem of arithmetic, every composite number can be uniquely written as the product of its prime factors. Thus, the given expression represents a composite number.
Application Of The Fundamental Theorem Of Arithmetic To Find The HCF And LCM Of Numbers
All composite numbers can be written as the product of two or more prime numbers. For example, 20 can be written as 22 × 5; 54 can be written as 2 × 33, and so on.
Note that if we do not consider the way in which the prime factors are written, then we can prime factorise every number in only one way. This applies to other numbers as well.
This leads to the fundamental theorem of arithmetic, which states that:

Even though we did not notice it before, whenever we prime factorise a number, we use the fundamental theorem of arithmetic to do so.
For example, the prime factorisation of 980 is represented as
980 = 2 × 490
= 2 × 2 × 245
= 2 × 2 × 5 × 49
= 2 × 2 × 5 × 7 × 7
= 22 × 51 × 72
Hence, 22 × 51 × 72 is the prime factorisation of 980; and 2, 5, and 7 are its prime factors.
By applying the fundamental theorem of arithmetic to the prime factorized numbers, we can also find their HCF and LCM.
This is known as the prime factorisation method, which states that:

Let us understand this method with the help of some examples.
Example 1: Find the LCM and the HCF of 432 and 676 using the prime factorization method.
Solution:
We can write these numbers as
432 = 24 × 33
676 = 22 × 132
To calculate the HCF
We observe that the only common prime factor is 2 and the smallest power of this prime factor is also 2.
Thus, HCF (432, 676) = 22 = 4
To calculate the LCM
We observe that the prime factors of 432 and 676 are 2, 3, and 13. The greatest powers of these factors are 4, 3, and 2 respectively.
LCM is the product of the greatest power of each prime factor.
Thus, LCM (432, 676) = 24 × 33 × 132 = 73008
Example 2: Find the HCF and the LCM of 28, 42, and 64 using the prime factorization method.
Solution:
We can write these numbers as
28 = 22 × 71
42 = 2 × 31 × 71
64 = 26
HCF is the product of the smallest power of each common prime factor. Here, the only common prime factor is 2 and its power is 1.
Thus, HCF (28, 42, 64) = 21 = 2
LCM is the product of the greatest power of each prime factor. Thus, LCM (28, 42, 64) = 26 × 31 × 71 = 1344
Example 3: Find the HCF and the LCM of 1080 and 900 using the prime factorization and show that HCF × LCM = Product of two numbers.
Solution:
1080 = 23 × 33 × 5
900 = 22 × 32 × 52
Hence, HCF (1080, 900) = 22 × 32 × 5 = 180
LCM (1080, 900) = 23 × 33 × 52 = 5400
HCF × LCM = 180 × 5400 = 972000
Product of numbers = 1080 × 900 = 972000
Hence, HCF × LCM = Product of two numbers
Example 4: The HCF of 273 and another number is 7, while their LCM is 3003. Find the other number.
Solution:
Let the first number (a) be 273 and the second number be b.
It is given that HCF (a, b) = 7 and LCM (a, b) = 3003.
We know that HCF  LCM = Product of two numbers.
LCM = Product of two numbers.
⇒ HCF (a, b) × LCM (a, b) = a × b
⇒ 7 × 3003 = 273 × b
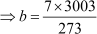
⇒ b = 77
Hence, the other number is 77.
Example 5: Anurag takes 6 minutes to complete one round of jogging around the circular track of a park, while Twinkle takes 8 minutes to do the same. If both of them start jogging at the same time from the same point, then how much time will they take before they meet at the point from which they started?
Solution:
Since Anurag and Twinkle take 6 minutes and 8 minutes respectively to complete one round of the circular track, the time after which they will meet at the starting point will be the lowest multiple of 6 and 8, i.e., their LCM.
6 = 2 × 3
8 = 23
∴ LCM (6, 8) = 23 × 3 = 24
Thus, they will meet at the starting point after 24 minutes.
Example 6: There are 120 students in a class. When the students were arranged according to their roll numbers, it was observed that every second student got distinction in Mathematics, every third student got distinction in Science, and every fifth student got distinction in English. How many students got distinction in all three subjects?
Solution:
As every second, third, and fifth student got distinction in Math, Science, and English respectively, the roll numbers of the students who got distinction in all three subjects will be equal to the multiples of the LCM of 2, 3, and 5.
LCM (2, 3, 5) = 2 × 3 × 5 = 30
Thus, every 30th student got distinction in all three subjects.
Thus, a total of 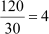 students got distinction in all three subjects.
students got distinction in all three subjects.
Properties Of Prime Numbers
Consider the number 8n, where n is a natural number.
Is there any value of n for which 8n ends with zero?
It is difficult to answer this question directly. However, we can answer this question by making use of the fundamental theorem of arithmetic. It states that

This means that if we are given a composite number, then that number can be written as a product of prime numbers in only one way (except for the order of prime numbers).
For example: the composite number 255 can be written as the product of primes as follows. 255 = 3 × 5 × 17
Also, 255 can be written as 3 × 17 × 5 or 5 × 3 × 17 or 5 × 17 × 3 or 17 × 3 × 5 or 17 × 5 × 3.
Thus, we can see that 255 can be expressed as a product of unique prime numbers 3, 5, and 17 but the order of representation may differ.
Now, by making use of the above theorem, we can answer the question which we were discussing in the beginning. Let us see how.
Suppose the number 8n ends with zero for some value of n. Since the number ends with zero, it should be divisible by 10. Now, 10 = 2 × 5
Thus, this number should be divisible by 2 and 5 also.
Therefore, the prime factorization of 8n should contain both the prime numbers 2 and 5. We have, 8n = (23)n = 23n
⇒ The only prime in the factorization of 8n is 2.
Thus, by fundamental theorem of arithmetic, there is no other prime in the factorization of 8n.
Hence, there is no natural number n for which 8n ends with the digit zero. In this way, we can make use of the above theorem.
Let us now look at some more examples to understand this concept better.
Example 1: Prove that the number 9n, where n is a natural number, cannot end with a zero.
Solution:
Suppose the number 9n ends with a zero for some value of n.
Since the number ends with zero, it should be divisible by 10.
Now, 10 = 2 × 5
Thus, this number should be divisible by 2 and 5 also.
Therefore, the prime factorization of 9n should contain both the prime numbers 2 and 5.
We have, 9n = (32)n = 32n
⇒ The only prime in the factorization of 9n is 3.
Thus, by fundamental theorem of arithmetic, there is no other prime in the factorization of 9n.
Hence, there is no natural number n for which 9n ends with the digit zero.
Example 2: Check whether the numbers 49n, where n is a natural number, can end with a zero.
Solution:
Suppose the number 49n ends with a zero for some value of n.
Since the number ends with zero, it should be divisible by 10.
Now, 10 = 2 × 5
Thus, this number should be divisible by 2 and 5 also.
Therefore, the prime factorization of 49n should contain both the prime numbers 2 and 5. We have, 49n = (72)n = 72n
⇒ The only prime in the factorization of 49n is 7.
Thus, by fundamental theorem of arithmetic, there is no other prime in the factorization of 49n.
Thus, there is no natural number n for which 49n ends with the digit zero.
3.Irrational and Rational Numbers
- Books Name
- Mathematics Book for CBSE Class 10
- Publication
- Carrier Point
- Course
- CBSE Class 10
- Subject
- Mathmatics
Revisiting Irrational Numbers
In Class IX, you were introduced to irrational numbers and many of their properties.
You studied about their existence and how the rationals and the irrationals together
made up the real numbers. You even studied how to locate irrationals on the number
line. However, we did not prove that they were irrationals. In this section, we will
prove that 2 , 3 , 5 and, in general, p is irrational, where p is a prime. One of
the theorems, we use in our proof, is the Fundamental Theorem of Arithmetic.
Recall, a number ‘s’ is called irrational if it cannot be written in the form ,
p
q
where p and q are integers and q ¹ 0. Some examples of irrational numbers, with
2018-19
12 MATHEMATICS
which you are already familiar, are :
2 2, 3, 15 , , , 0.10110111011110 . . .
3
p − , etc.
Before we prove that 2 is irrational, we need the following theorem, whose
proof is based on the Fundamental Theorem of Arithmetic.
Theorem 1.3 : Let p be a prime number. If p divides a2, then p divides a, where
a is a positive integer.
*Proof : Let the prime factorisation of a be as follows :
a = p1p2 . . . pn, where p1,p2, . . ., pn are primes, not necessarily distinct.
Therefore, a2 = (p1p2 . . . pn)( p1 p 2 . . . pn) = p2
1p2
2 . . . p2
n.
Now, we are given that p divides a2. Therefore, from the Fundamental Theorem of
Arithmetic, it follows that p is one of the prime factors of a2. However, using the
uniqueness part of the Fundamental Theorem of Arithmetic, we realise that the only
prime factors of a2 are p
1, p
2, . . ., p
n. So p is one of p
1, p
2, . . ., p
n.
Now, since a = p1 p2 . . . pn, p divides a.
We are now ready to give a proof that 2 is irrational.
The proof is based on a technique called ‘proof by contradiction’. (This technique is
discussed in some detail in Appendix 1).
Theorem 1.4 : 2 is irrational.
Proof : Let us assume, to the contrary, that 2 is rational.
So, we can find integers r and s (¹ 0) such that 2 =
r
s
.
Suppose r and s have a common factor other than 1. Then, we divide by the common
factor to get 2 ,
a
b
= where a and b are coprime.
So, b 2 = a.
Squaring on both sides and rearranging, we get 2b2 = a2. Therefore, 2 divides a2.
Now, by Theorem 1.3, it follows that 2 divides a.
So, we can write a = 2c for some integer c.
* Not from the examination point of view.
2018-19
REAL NUMBERS 13
Substituting for a, we get 2b2 = 4c2, that is, b2 = 2c2.
This means that 2 divides b2, and so 2 divides b (again using Theorem 1.3 with p = 2).
Therefore, a and b have at least 2 as a common factor.
But this contradicts the fact that a and b have no common factors other than 1.
This contradiction has arisen because of our incorrect assumption that 2 is rational.
So, we conclude that 2 is irrational.
Example 9 : Prove that 3 is irrational.
Solution : Let us assume, to the contrary, that 3 is rational.
That is, we can find integers a and b (¹ 0) such that 3 =
a
b
×
Suppose a and b have a common factor other than 1, then we can divide by the
common factor, and assume that a and b are coprime.
So, b 3 = a×
Squaring on both sides, and rearranging, we get 3b2 = a2.
Therefore, a2 is divisible by 3, and by Theorem 1.3, it follows that a is also divisible
by 3.
So, we can write a = 3c for some integer c.
Substituting for a, we get 3b2 = 9c2, that is, b2 = 3c2.
This means that b2 is divisible by 3, and so b is also divisible by 3 (using Theorem 1.3
with p = 3).
Therefore, a and b have at least 3 as a common factor.
But this contradicts the fact that a and b are coprime.
This contradiction has arisen because of our incorrect assumption that 3 is rational.
So, we conclude that 3 is irrational.
In Class IX, we mentioned that :
l the sum or difference of a rational and an irrational number is irrational and
l the product and quotient of a non-zero rational and irrational number is
irrational.
We prove some particular cases here.
2018-19
14 MATHEMATICS
Example 10 : Show that 5 – 3 is irrational.
Solution : Let us assume, to the contrary, that 5 – 3 is rational.
That is, we can find coprime a and b (b ¹ 0) such that 5 3
a
b
− = ×
Therefore, 5 3
a
b
− = ×
Rearranging this equation, we get
5
3 5 –
a b a
b b
−
= = ×
Since a and b are integers, we get 5 –
a
b
is rational, and so 3 is rational.
But this contradicts the fact that 3 is irrational.
This contradiction has arisen because of our incorrect assumption that 5 – 3 is
rational.
So, we conclude that 5 − 3 is irrational.
Example 11 : Show that 3 2 is irrational.
Solution : Let us assume, to the contrary, that 3 2 is rational.
That is, we can find coprime a and b (b ¹ 0) such that 3 2
a
b
= ×
Rearranging, we get 2
3
a
b
= ×
Since 3, a and b are integers,
3
a
b
is rational, and so 2 is rational.
But this contradicts the fact that 2 is irrational.
So, we conclude that 3 2 is irrational.
3.Irrational and Rational Numbers


3.Irrational and Rational Numbers
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
1.3 Irrational Numbers :

Some Properties of irrational numbers :
(a) The –ve of an irrational number is an irrational number.
(b) The sum of a rational and an irrational number is an irrational number.
(c) The product of a non–zero rational number with an irrational number is always an irrational number.
3.Irrational and Rational Numbers
Irrational Numbers
We know that a number which cannot be written in the form of ,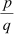 where p and q are integers and q ≠ 0, is known as an irrational number.
where p and q are integers and q ≠ 0, is known as an irrational number.
For example: all numbers of the form ,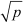 where p is a prime number such as etc.,
where p is a prime number such as etc., 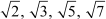 are irrational numbers.
are irrational numbers.
How can we prove that these are irrational numbers?
We can prove this by making use of a theorem which can be stated as follows.
“If p divides a2, then p divides a (where p is a prime number and a is a positive integer)”.

So go through the given video to understand the application of the above stated property.
Similarly, we can prove that square roots of other prime numbers like ,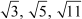 etc. are irrational numbers.
etc. are irrational numbers.
Besides these irrational numbers, there are some other irrational numbers like etc.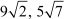
We can also prove why these numbers are irrational. Before this, let us first see what happens to irrational numbers, when we apply certain mathematical operations on them.

We will now prove that 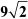 is irrational.
is irrational.
We know that 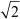 is irrational (as proved before).
is irrational (as proved before).
Now, the multiplication of a rational and an irrational number gives an irrational number. Therefore, 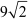 is an irrational number.
is an irrational number.
Let us now try to understand the concept further through some more examples.
Example 1: Prove that 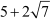 is irrational. Solution:
is irrational. Solution:
Let us assume that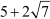 is not irrational, i.e.
is not irrational, i.e.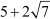 is a rational number.
is a rational number.
Then we can write ,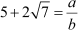 where a and b are integers andb ≠ 0.
where a and b are integers andb ≠ 0.
Let a and b have a common factor other than 1.
After dividing by the common factor, we obtain
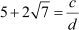 , where c and d are co-prime numbers.
, where c and d are co-prime numbers.
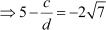
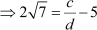
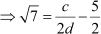
As c, d and 2 are integers, 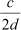 and
and 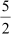 are rational numbers.
are rational numbers.
Thus,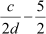 is rational.
is rational.
![]() is rational as the difference of two rational numbers is again a rational number.
is rational as the difference of two rational numbers is again a rational number.
This is a contradiction as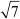 is irrational.
is irrational.
Therefore, our assumption that 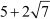 is rational is wrong.
is rational is wrong.
Hence, 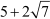 is irrational.
is irrational.
Example 2: Prove that 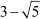 is irrational.
is irrational.
Solution:
Let us assume 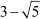 is rational. Then, we can write
is rational. Then, we can write
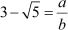 ,
,
where a and b are co-prime and b ≠ 0.
⇒![]()
Now, as a and b are integers,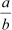 is rational or
is rational or 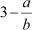 is a rational number.
is a rational number.
This means that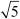 is rational.
is rational.
This is a contradiction as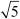 is irrational.
is irrational.
Therefore, our assumption that 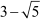 is rational is wrong.
is rational is wrong.
Hence, 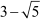 is an irrational number.
is an irrational number.
Decimal Expansions of Rational Numbers
The Need for Converting Rational Numbers into Decimals
A carpenter wishes to make a point on the edge of a wooden plank at 95 mm from any end. He has a centimeter tape, but how can he use that to mark the required point?
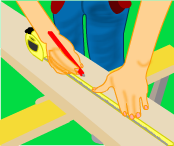
Simple! He should convert 95 mm into its corresponding centimeter value, i.e., 9.5 cm and then measure and mark the required length on the wooden plank.
This is just one of the many situations in life when we face the need to convert numbers into decimals. In this lesson, we will learn to convert rational numbers into decimals, observe the types of decimal numbers, and solve a few examples based on this concept.
Know More
Two rational numbers 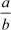 and
and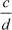 are equal if and only if ad = bc.
are equal if and only if ad = bc.
Take, for example, the rational numbers 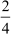 and
and 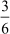 . Let us see if they are equal or not. Here, a = 2, b = 4, c = 3 and d = 6
. Let us see if they are equal or not. Here, a = 2, b = 4, c = 3 and d = 6
Now, we have:
ad = 2 × 6 = 12
bc = 4 × 3 = 12
Since ad = bc, we obtain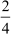 = .
= .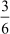
We know that the form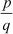 represents the division of integer p by the integer q. By solving
represents the division of integer p by the integer q. By solving
this division, we can find the decimal equivalent of the rational number 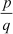 . Now, let us convert the numbers
. Now, let us convert the numbers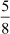 ,
, 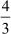 and
and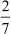 into decimals using the long division method.
into decimals using the long division method.
![]()
![]()
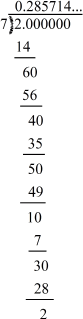
While the remainder is zero in the division of 5 by 8, it is not so in case of the other two divisions. Thus, we can get two different cases in the decimal expansions of rational numbers.
Observing the Decimal Expansions of Rational Numbers
We can get the following two cases in the decimal expansions of rational numbers.
Case I: When the remainder is zero
In this case, the remainder becomes zero and the quotient or decimal expansion terminates after a finite number of digits after the decimal point. For example, in the decimal
expansion of , 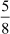 we get the remainder as zero and the quotient as 0.625.
we get the remainder as zero and the quotient as 0.625.
Case II: When the remainder is never zero
In this case, the remainder never becomes zero and the corresponding decimal expansion
is non-terminating. For example, in the decimal expansions of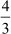 and
and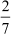 , we see that the remainder never becomes zero and their corresponding quotients are non-terminating decimals.
, we see that the remainder never becomes zero and their corresponding quotients are non-terminating decimals.
When we divide 4 by 3 and 2 by 7, we get 1.3333… and 0.285714285714… as the respective quotients. In these decimal numbers, the digit ‘3’ and the group of digits
‘285714’ get repeated. Therefore, we can write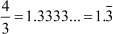 and
and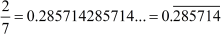
Here, the symbol  indicates the digit or group of digits
indicates the digit or group of digits
that gets repeated.
Solved Examples
Example 1: Write the decimal expansion of 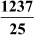 and find if it is terminating or non- terminating and repeating.
and find if it is terminating or non- terminating and repeating.
Solution:
Here is the long division method to find the decimal expansion of .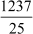
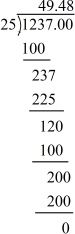
Hence, the decimal expansion of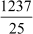 is 49.48. Since the remainder is obtained as zero, the decimal numberis terminating.
is 49.48. Since the remainder is obtained as zero, the decimal numberis terminating.
Example 2: Write the decimal expansion of 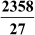 and find if it is terminating or non- terminating and repeating.
and find if it is terminating or non- terminating and repeating.
Solution:
Here is the long division method to find the decimal expansion of .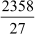
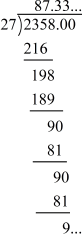
Hence, the decimal expansion of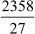 is 87.33 Since the remainder 9 is obtained again
is 87.33 Since the remainder 9 is obtained again
and again, the decimal numberis non-terminating and repeating. The decimal number can also be written as .![]()
Medium
Example 1: Find the decimal expansion of each of the following rational numbers and write the nature of the same.
1.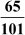
2.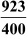
3.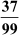
4.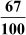
Solution:
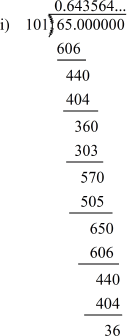
We have 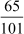 = 0.64356435... =
= 0.64356435... =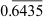
The group of digits ‘6435’ repeats after the decimal point. Hence, the decimal expansion of the given rational number is non-terminating and repeating.
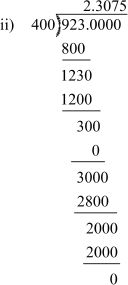
We have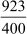 = 2.3075
= 2.3075
Hence, the given rational number has a terminating decimal expansion.
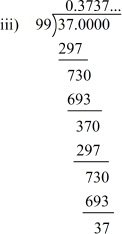
We have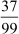 = 0.3737... =
= 0.3737... =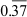
The pair of digits ‘37’ repeats after the decimal point. Hence, the decimal expansion of the given rational number is non-terminating and repeating.
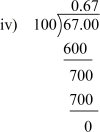
We have![]() = 0.67
= 0.67
Hence, the given rational number has a terminating decimal expansion.
Terminating and Non-terminating Repeating Decimal Expansions of Rational Numbers
We can find the decimal expansion of rational numbers using long division method.
However, it is possible to check whether the decimal expansion is terminating or non- terminating without actually carrying out long division also.
Let us start by taking a few rational numbers in the decimal form.
(a)
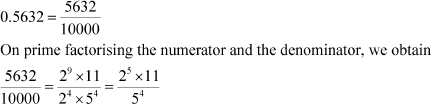
(b)
0.275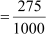
On prime factorizing the numerator and the denominator, we obtain
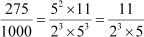
Can you see a pattern in the two examples?
We notice that the given examples are rational numbers with terminating decimal expansions. When they are written in the 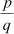 form, where p and q are co-prime
form, where p and q are co-prime
(the HCF of p and q is 1), the denominator, when written in the form of prime factors, has 2 or 5 or both.
The above observation brings us to the given theorem.
If x is a rational number with terminating decimal expansion, then it can be expressedin the 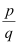 form, where p and q are co-prime (the HCF of p and q is 1) and the prime factorisation of q is of the form 2n5m, where n and m are non-negative integers.
form, where p and q are co-prime (the HCF of p and q is 1) and the prime factorisation of q is of the form 2n5m, where n and m are non-negative integers.
Contrary to this, if the prime factorisation of q is not of the form 2n5m, where n and m are non-negative integers, then the decimal expansion is a
non-terminating one.
Let us see a few examples that will help verify this theorem.
(a)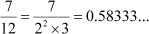
(b)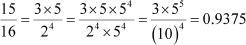
(c) 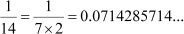
(d) 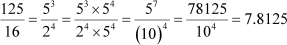
Note that in examples (b) and (d), each of the denominators is composed only of the prime factors 2 and 5, because of which, the decimal expansion is terminating. However, in examples (a) and (c), each of the denominators has at least one prime factor other than 2 and 5 in their prime factorisation, because of which, the decimal expansion is non- terminating and repetitive.
To summarize the above results, we can say that:

Let us solve a few examples to understand this concept better.
Example 1: Without carrying out the actual division, find if the following rational numbers have a terminating or a non-terminating decimal expansion.
(a)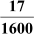
(b) 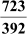
Solution:
(a)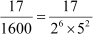
As the denominator can be written in the form 2n5m, where n = 6 and m = 2 are non-negative integers, the given rational number has a terminating decimal expansion.
(b)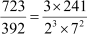
As denominator cannot be written in the form 2n5m, where n and m are non-negative integers, the given rational number has a non-terminating decimal expansion.
Example 2: Without carrying out the actual division, find if the expression 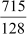 has a terminating or a non-terminating decimal expansion.
has a terminating or a non-terminating decimal expansion.
Solution: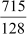 =
=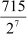
As the denominator can be written in the form 2n5m, where n = 7and m = 0 are non-negative integers, the given rational number has a terminating decimal expansion.
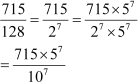
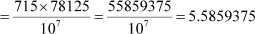
Hence, 5.5859375 is the decimal expansion of the given rational number.
3.Irrational and Rational Numbers
- Books Name
- Sample paper Term II Maths
- Publication
- SonikaAnandAcademy
- Course
- CBSE Class 10
- Subject
- Mathmatics
There are two types of Real numbers
Rational
Irrrational
Rational numbers are of form p/q and terminating. Eg 5/7
Irrational numbers are repeated eg √2+5
decimal expansions of rational numbers in terms of terminating/non-terminating recurring decimals
- Books Name
- Mathematics Book for CBSE Class 10
- Publication
- Carrier Point
- Course
- CBSE Class 10
- Subject
- Mathmatics
Revisiting Rational Numbers and Their Decimal Expansions
In Class IX, you studied that rational numbers have either a terminating decimal
expansion or a non-terminating repeating decimal expansion. In this section, we are
going to consider a rational number, say ( 0)
p
q
q
¹ , and explore exactly when the
decimal expansion of
p
q
is terminating and when it is non-terminating repeating
(or recurring). We do so by considering several examples.
Let us consider the following rational numbers :
(i) 0.375 (ii) 0.104 (iii) 0.0875 (iv) 23.3408.
Now (i)
3
375 375
0.375
1000 10
= = (ii)
3
104 104
0.104
1000 10
= =
(iii)
4
875 875
0.0875
10000 10
= = (iv)
4
233408 233408
23.3408
10000 10
= =
As one would expect, they can all be expressed as rational numbers whose
denominators are powers of 10. Let us try and cancel the common factors between
the numerator and denominator and see what we get :
(i)
3
3 3 3 3
375 3 5 3
0.375
10 2 5 2
×
= = =
×
(ii)
3
3 3 3 3
104 13 2 13
0.104
10 2 5 5
×
= = =
×
(iii)
4 4
875 7
0.0875
10 2 5
= =
×
(iv)
2
4 4
233408 2 7 521
23.3408
10 5
× ×
= =
Do you see any pattern? It appears that, we have converted a real number
whose decimal expansion terminates into a rational number of the form ,
p
q
where p
and q are coprime, and the prime factorisation of the denominator (that is, q) has only
powers of 2, or powers of 5, or both. We should expect the denominator to look like
this, since powers of 10 can only have powers of 2 and 5 as factors.
Even though, we have worked only with a few examples, you can see that any
real number which has a decimal expansion that terminates can be expressed as a
rational number whose denominator is a power of 10. Also the only prime factors of 10
are 2 and 5. So, cancelling out the common factors between the numerator and the
denominator, we find that this real number is a rational number of the form ,
p
q
where
the prime factorisation of q is of the form 2n5m, and n, m are some non-negative integers.
Let us write our result formally:
2018-19
16 MATHEMATICS
Theorem 1.5 : Let x be a rational number whose decimal expansion terminates.
Then x can be expressed in the form ,
p
q
where p and q are coprime, and the
prime factorisation of q is of the form 2n5m, where n, m are non-negative integers.
You are probably wondering what happens the other way round in Theorem 1.5.
That is, if we have a rational number of the form ,
p
q
and the prime factorisation of q
is of the form 2n5m, where n, m are non negative integers, then does
p
q
have a
terminating decimal expansion?
Let us see if there is some obvious reason why this is true. You will surely agree
that any rational number of the form ,
a
b
where b is a power of 10, will have a terminating
decimal expansion. So it seems to make sense to convert a rational number of the
form
p
q
, where q is of the form 2n5m, to an equivalent rational number of the form ,
a
b
where b is a power of 10. Let us go back to our examples above and work backwards.
(i)
3
3 3 3 3
3 3 3 5 375
0.375
8 2 2 5 10
×
= = = =
×
(ii)
3
3 3 3 3
13 13 13 2 104
0.104
125 5 2 5 10
×
= = = =
×
(iii)
3
4 4 4 4
7 7 7 5 875
0.0875
80 2 5 2 5 10
×
= = = =
× ×
(iv)
2 6
4 4 4 4
14588 2 7 521 2 7 521 233408
23.3408
625 5 2 5 10
× × × ×
= = = =
×
So, these examples show us how we can convert a rational number of the form
p
q
, where q is of the form 2n5m, to an equivalent rational number of the form ,
a
b
where b is a power of 10. Therefore, the decimal expansion of such a rational number
terminates. Let us write down our result formally.
Theorem 1.6 : Let x =
p
q
be a rational number, such that the prime factorisation
of q is of the form 2n5m, where n, m are non-negative integers. Then x has a
decimal expansion which terminates.
2018-19
REAL NUMBERS 17
We are now ready to move on to the rational numbers
whose decimal expansions are non-terminating and recurring.
Once again, let us look at an example to see what is going on.
We refer to Example 5, Chapter 1, from your Class IX
textbook, namely,
1
7
. Here, remainders are 3, 2, 6, 4, 5, 1, 3,
2, 6, 4, 5, 1, . . . and divisor is 7.
Notice that the denominator here, i.e., 7 is clearly not of
the form 2n5m. Therefore, from Theorems 1.5 and 1.6, we
know that
1
7
will not have a terminating decimal expansion.
Hence, 0 will not show up as a remainder (Why?), and the
remainders will start repeating after a certain stage. So, we
will have a block of digits, namely, 142857, repeating in the
quotient of
1
7
.
What we have seen, in the case of
1
7
, is true for any rational number not covered
by Theorems 1.5 and 1.6. For such numbers we have :
Theorem 1.7 : Let x =
p
q
be a rational number, such that the prime factorisation
of q is not of the form 2n5m, where n, m are non-negative integers. Then, x has a
decimal expansion which is non-terminating repeating (recurring).
From the discussion above, we can conclude that the decimal expansion of
every rational number is either terminating or non-terminating repeating.
decimal expansions of rational numbers in terms of terminating/non-terminating recurring decimals
Decimal Expansion Of Rational Numbers
Before going into a representation of the decimal expansion of rational numbers, let us understand what rational numbers are. Any number that can be represented in the form of p/q, such that p and q are integers and q ≠ 0 are known as rational numbers. So when these numbers have been simplified further, they result in decimals. Let us learn how to expand such decimals here.
Examples: 6 , -8.1,\frac{4}{5} etc. are all examples of rational numbers.
How to Expand Rational Numbers in Decimals?
The real numbers which are recurring or terminating in nature are generally rational numbers.

For example, consider the number 33.33333……. It is a rational number as it can be represented in the form of 100/3. It can be seen that the decimal part .333…… is the non-terminating repeating part, i .e. it is a recurring decimal number.
Also the terminating decimals such as 0.375, 0.6 etc. which satisfy the condition of being rational (0.375 = \frac{3}{2^3} ,0.6 = \frac{3}{5}).
Consider any decimal number. For e.g. 0.567. It can be written as 567/1000 or \frac{567}{10^3} . Similarly, the numbers 0.6689,0.032 and .45 can be written as \frac{6689}{10^4} ,\frac{32}{10^3} and \frac{45}{10^2} respectively in fractional form.
Thus, it can be seen that any decimal number can be represented as a fraction which has denominator in powers of 10. We know that prime factors of 10 are 2 and 5, it can be concluded that any decimal rational number can be easily represented in the form of \frac{p}{q}, such that p and q are integers and the prime factorization of q is of the form 2^x~ 5^y, where x and y are non-negative integers.
This statement gives rise to a very important theorem.
Theorems
Theorem 1: If m be any rational number whose decimal expansion is terminating in nature, then m can be expressed in form of \frac{p}{q}, where p and q are co-primes and the prime factorization of q is of the form 2^x~ 5^y, where x and y are non-negative integers.
The converse of this theorem is also true and it can be stated as follows:
Theorem 2: If m is a rational number, which can be represented as the ratio of two integers i.e. \frac{p}{q} and the prime factorization of q takes the form 2^x~ 5^y, where x and y are non-negative integers then, then it can be said that m has a decimal expansion which is terminating.
Consider the following examples:
- \frac{7}{8} = \frac{7}{2^3} = \frac{7~×~5^3}{2^3~×~5^3} = \frac{875}{10^3}
- \frac{3}{80} = \frac{3}{2^4~×~5} = \frac{3~×~5^3}{2^4~×~5^4} = \frac{375}{10^4}
Moving on, to decimal expansion of rational numbers which are recurring, the following theorem can be stated:
Theorem 3: If m is a rational number, which can be represented as the ratio of two integers i.e. \frac{p}{q} and the prime factorization of q does not takes the form 2^x~ 5^y, where x and y are non-negative integers. Then, it can be said that m has a decimal expansion which is non-terminating repeating (recurring).
Consider the following examples:
- \frac{1}{6} = 0.1666…. = 0.1\overline{6}
- \frac{7}{12} = 0.58333… = 0.58\overline{3}
- \frac{9}{11} = 0.8181… = 0.\overline{81}
Rational Number to decimal Examples
Case 1: Remainder equal to zero
Example: Find the decimal expansion of 3/6.

Here, the quotient is 0.5 and the remainder is 0. Rational number 3/6 results in a terminating decimal.
Case 2: Remainder not equal to zero
Example: Express 5/13 in decimal form.

Here, the quotient is 0.384615384 and the remainder is not zero. Notice that the number…384 after the decimal is repeating. Hence, 5/13 gives us a non-terminating recurring decimal expansion. And this can be written as 5/13=![]()
A rational number gives either terminating or non-terminating recurring decimal expansion. Thus, we can say that a number whose decimal expansion is terminating or non-terminating recurring is rational.
Find the joy in learning with us. To know more about rational numbers please visit our website www.byjus.com and download BYJU’S-The Learning App from Google play store to learn anytime anywhere.
decimal expansions of rational numbers in terms of terminating/non-terminating recurring decimals
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
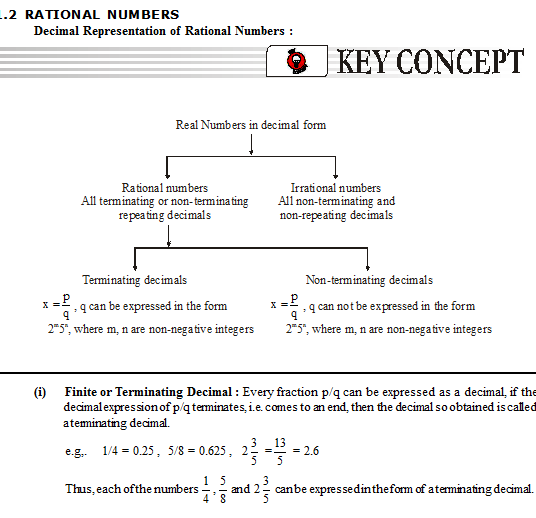


Quadratic Equations
- Books Name
- Mathematics Book for CBSE Class 10
- Publication
- Carrier Point
- Course
- CBSE Class 10
- Subject
- Mathmatics
Notes on Quadratic Equations
Quadratic Polynomial
A polynomial, whose degree is 2, is called a quadratic polynomial. It is in the form of
p(x) = ax2 + bx + c, where a ≠ 0
Quadratic Equation
When we equate the quadratic polynomial to zero then it is called a Quadratic Equation i.e. if
p(x) = 0, then it is known as Quadratic Equation.
Standard form of Quadratic Equation

where a, b, c are the real numbers and a≠0
Types of Quadratic Equations
1. Complete Quadratic Equation ax2 + bx + c = 0, where a ≠ 0, b ≠ 0, c ≠ 0
2. Pure Quadratic Equation ax2 = 0, where a ≠ 0, b = 0, c = 0
Roots of a Quadratic Equation
Let x = α where α is a real number. If α satisfies the Quadratic Equation ax2+ bx + c = 0 such that aα2 + bα + c = 0, then α is the root of the Quadratic Equation.
As quadratic polynomials have degree 2, therefore Quadratic Equations can have two roots. So the zeros of quadratic polynomial p(x) =ax2+bx+c is same as the roots of the Quadratic Equation ax2+ bx + c= 0.
Methods to solve the Quadratic Equations
There are three methods to solve the Quadratic Equations-
1. Factorisation Method
In this method, we factorise the equation into two linear factors and equate each factor to zero to find the roots of the given equation.
Step 1: Given Quadratic Equation in the form of ax2 + bx + c = 0.
Step 2: Split the middle term bx as mx + nx so that the sum of m and n is equal to b and the product of m and n is equal to ac.
Step 3: By factorization we get the two linear factors (x + p) and (x + q)
ax2 + bx + c = 0 = (x + p) (x + q) = 0
Step 4: Now we have to equate each factor to zero to find the value of x.

These values of x are the two roots of the given Quadratic Equation.
2. Completing the square method
In this method, we convert the equation in the square form (x + a)2 - b2 = 0 to find the roots.
Step1: Given Quadratic Equation in the standard form ax2 + bx + c = 0.
Step 2: Divide both sides by a

Step 3: Transfer the constant on RHS then add square of the half of the coefficient of x i.e. on both sides
on both sides


Step 4: Now write LHS as perfect square and simplify the RHS.

Step 5: Take the square root on both the sides.

Step 6: Now shift all the constant terms to the RHS and we can calculate the value of x as there is no variable at the RHS.

3. Quadratic formula method
In this method, we can find the roots by using quadratic formula. The quadratic formula is

where a, b and c are the real numbers and b2 – 4ac is called discriminant.
To find the roots of the equation, put the value of a, b and c in the quadratic formula.
Nature of Roots
From the quadratic formula, we can see that the two roots of the Quadratic Equation are -

Where D = b2 – 4ac
The nature of the roots of the equation depends upon the value of D, so it is called the discriminant.

∆ = Discriminant

Quadratic Equations
Quadratic Equation
When we equate a quadratic polynomial to a constant, we get a quadratic equation.
Any equation of the form p(x)=c, where p(x) is a polynomial of degree 2 and c is a constant, is a quadratic equation.
The standard form of a Quadratic Equation
The standard form of a quadratic equation is ax2+bx+c=0, where a,b and c are real numbers and a≠0.
‘a’ is the coefficient of x2. It is called the quadratic coefficient. ‘b’ is the coefficient of x. It is called the linear coefficient. ‘c’ is the constant term.
Solving QE by Factorisation
Roots of a Quadratic equation
The values of x for which a quadratic equation is satisfied are called the roots of the quadratic equation.
If α is a root of the quadratic equation ax2+bx+c=0, then aα2+bα+c=0.
A quadratic equation can have two distinct real roots, two equal roots or real roots may not exist.
Graphically, the roots of a quadratic equation are the points where the graph of the quadratic polynomial cuts the x-axis.
Consider the graph of a quadratic equation x2−4=0:

Graph of a Quadratic Equation
In the above figure, -2 and 2 are the roots of the quadratic equation x2−4=0
Note:
- If the graph of the quadratic polynomial cuts the x-axis at two distinct points, then it has real and distinct roots.
- If the graph of the quadratic polynomial touches the x-axis, then it has real and equal roots.
- If the graph of the quadratic polynomial does not cut or touch the x-axis then it does not have any real roots.
Solving a Quadratic Equation by Factorization method
Consider a quadratic equation 2x2−5x+3=0
⇒2x2−2x−3x+3=0
This step is splitting the middle term
We split the middle term by finding two numbers (-2 and -3) such that their sum is equal to the coefficient of x and their product is equal to the product of the coefficient of x2 and the constant.
(-2) + (-3) = (-5)
And (-2) × (-3) = 6
2x2−2x−3x+3=0
2x(x−1)−3(x−1)=0
(x−1)(2x−3)=0
In this step, we have expressed the quadratic polynomial as a product of its factors.
Thus, x = 1 and x =3/2 are the roots of the given quadratic equation.
This method of solving a quadratic equation is called the factorisation method.
69,766
Solving QE by Completing the Square
Solving a Quadratic Equation by Completion of squares method
In the method of completing the squares, the quadratic equation is expressed in the form (x±k)2=p2.
Consider the quadratic equation 2x2−8x=10
(i) Express the quadratic equation in standard form.
2x2−8x−10=0
(ii) Divide the equation by the coefficient of x2 to make the coefficient of x2 equal to 1.
x2−4x−5=0
(iii) Add the square of half of the coefficient of x to both sides of the equation to get an expression of the form x2±2kx+k2.
(x2−4x+4)−5=0+4
(iv) Isolate the above expression, (x±k)2 on the LHS to obtain an equation of the form (x±k)2=p2
(x−2)2=9
(v) Take the positive and negative square roots.
x−2=±3
x=−1 or x=5
Solving QE Using Quadratic Formula
Quadratic Formula
Quadratic Formula is used to directly obtain the roots of a quadratic equation from the standard form of the equation.
For the quadratic equation ax2+bx+c=0,
x= [-b± √(b2-4ac)]/2a
By substituting the values of a,b and c, we can directly get the roots of the equation.
Discriminant
For a quadratic equation of the form ax2+bx+c=0, the expression b2−4ac is called the discriminant, (denoted by D), of the quadratic equation.
The discriminant determines the nature of roots of the quadratic equation based on the coefficients of the quadratic equation.
13,531
Solving using Quadratic Formula when D>0
Solve 2x2−7x+3=0 using the quadratic formula.
(i) Identify the coefficients of the quadratic equation. a = 2,b = -7,c = 3
(ii) Calculate the discriminant, b2−4ac
D=(−7)2−4×2×3= 49-24 = 25
D> 0, therefore, the roots are distinct.
(iii) Substitute the coefficients in the quadratic formula to find the roots
x= [-(-7)± √((-7)2-4(2)(3))]/2(2)
x=(7 ±5)/4
x=3 and x= 1/2 are the roots.
Nature of Roots
Based on the value of the discriminant, D=b2−4ac, the roots of a quadratic equation can be of three types.
Case 1: If D>0, the equation has two distinct real roots.
Case 2: If D=0, the equation has two equal real roots.
Case 3: If D<0, the equation has no real roots.
31,158
7,086
To know more about Nature of Roots, visit here.
Be More Curious
Graphical Representation of a Quadratic Equation
The graph of a quadratic polynomial is a parabola. The roots of a quadratic equation are the points where the parabola cuts the x-axis i.e. the points where the value of the quadratic polynomial is zero.
Now, the graph of x2+5x+6=0 is:

In the above figure, -2 and -3 are the roots of the quadratic equation
x2+5x+6=0.
For a quadratic polynomial ax2+bx+c,
If a>0, the parabola opens upwards.
If a<0, the parabola opens downwards.
If a = 0, the polynomial will become a first-degree polynomial and its graph is linear.
The discriminant, D=b2−4ac

Nature of graph for different values of D.
If D>0, the parabola cuts the x-axis at exactly two distinct points. The roots are distinct. This case is shown in the above figure in a, where the quadratic polynomial cuts the x-axis at two distinct points.
If D=0, the parabola just touches the x-axis at one point and the rest of the parabola lies above or below the x-axis. In this case, the roots are equal.
This case is shown in the above figure in b, where the quadratic polynomial touches the x-axis at only one point.
If D<0, the parabola lies entirely above or below the x-axis and there is no point of contact with the x-axis. In this case, there are no real roots.
This case is shown in the above figure in c, where the quadratic polynomial neither cuts nor touches the x-axis.
Formation of a quadratic equation from its roots
To find out the standard form of a quadratic equation when the roots are given:
Let α and β be the roots of the quadratic equation ax2+bx+c=0. Then,
(x−α)(x−β)=0
On expanding, we get,
x2−(α+β)x+αβ=0, which is the standard form of the quadratic equation. Here, a=1,b=−(α+β) and c=αβ.
Sum and Product of Roots of a Quadratic equation
Let α and β be the roots of the quadratic equation ax2+bx+c=0. Then,
Sum of roots =α+β=-b/a
Product of roots =αβ= c/a

 Carrier Point
Carrier Point
 Success Academy
Success Academy
 ACERISE INDIA
ACERISE INDIA


