2.Zeros and Coefficients of Polynomial – 1

Relationship Between Zeroes Of A Polynomial And Its Coefficients

We have learnt to find the zeroes or roots of a polynomial. Also, we know that zeroes or roots of a polynomial are those values of its variables for which the polynomial results to zero.

Now, let us learn about the relation between zeroes and the coefficients of the polynomial.

Relationship between the zero and the coefficient of a linear polynomial:

Let p(x) = ax + b be a linear polynomial such that a ≠ 0.

Zero of this polynomial can be obtained by equating it with 0. i.e, p(x) = 0

⇒ ax + b = 0

⇒ ax = –b

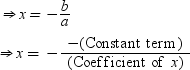
Using this relation, we can find the zero of a linear polynomial.

Relationship between the zeroes and the coefficients of a quadratic polynomial:

Consider a quadratic polynomial p(x) = 3x²– 5x – 12.

Can we find out the sum and the product of the zeroes of this polynomial?

Yes, we can find the sum and the product of zeroes but firstly we have to find out the zeroes of the polynomial.

Here, the zeroes of polynomial p(x) are 3 and .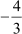

Now, the sum of zeroes = 3 +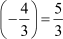

And the product of zeroes = 3 ×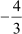 = – 4

Can we find out the sum and the product of zeroes by any other method?

Yes, there is also a method in which there is no need to find out the zeroes. In that method we use the coefficients of the polynomial to find the sum and the product of zeroes.

Firstly let us see the relation between the sum and product of zeroes and the coefficients of the polynomial.

Let us first consider a quadratic polynomial p(x) = ax² + bx + c, where a, b and c are constants.

If αand β are the zeroes of p(x) = ax² + bx + c, then,

Now, let us find the sum and product of zeroes of the polynomial given in the beginning, using these relations.

The polynomial is p(x) = 3x² – 5x – 12.

On comparing this equation with ax² + bx + c, we have

a = 3, b = –5 and c = –12

∴ Sum of zeroes = – =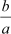

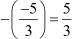
And the product of zeroes =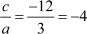

Using these relations we obtained the same values as we found after calculating the zeroes.

Now, let us know the relations between the sum and the product of zeroes and the coefficients of a cubic polynomial.

The general form of a cubic polynomial is p(x) = ax³ + bx² + cx + d where a, b, c and d are constants.

If α, β and γ are the three zeroes of cubic polynomial p(x), then the relations are given by

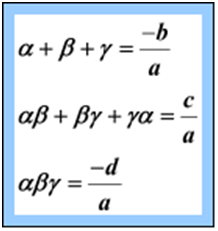
Let us solve some more problems to have a better understanding of the concept.

Example 1: Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.

(a) x² – 9x + 20 (b) 5x² + 21x – 20.

Solution:

(a)    The given quadratic polynomial is p(x) = x² – 9x + 20.

Firstly we will find the zeroes by the method of splitting the middle term and then verify the relationship between the zeroes and the coefficients of the polynomial.

In this method, we have to find two numbers whose product is 20 and sum (or difference) is 9.

Such two numbers are 4 and 5 so, we have

x² – 9x + 20 = x² – (4 + 5)x + 20

= x² – 4x – 5x + 20

= x (x – 4) – 5 (x – 4)

= (x – 4) (x – 5)

Thus, for finding zeroes, we put

x² – 9x + 20 = 0.

(x – 4) (x – 5) = 0

(x – 4) = 0 or (x – 5) = 0

x = 4 or 5

Thus, 4 and 5 are the zeroes of the polynomial p(x) = x² – 9x + 20.

Now sum of zeroes = 4 + 5 = 9

And product of zeroes = 4 × 5 = 20

Now, on comparing p(x) = x² – 9x + 20 with the general quadratic polynomial

ax² + bx + c = 0, we have a = 1, b = –9 and c = 20.

Using the formulae, we have

Sum of zeroes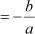

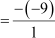
= 9

Product of zeroes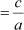

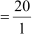
= 20

Hence, it is verified that Sum of zeroes = 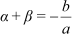and

Product of zeroes = αβ = .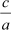

(b) Comparing the given polynomial with ax² + bx + c, we have, a = 5, b = 21

and c = – 20.

Using the method of splitting the middle term we have,

p(x) = 5x² + 21 x – 20 = 5x² + (25 – 4)x – 20

= 5x² + 25x –4 x – 20

= 5x(x + 5) –4 (x + 5)

= (x + 5) (5x – 4)

For finding zeroes, put p(x) = 0 (x + 5) (5x – 4) = 0

x = – 5 or x =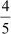

Thus, the zeroes of the polynomial 5x² + 21 x – 20 are – 5 and .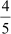

Now, sum of zeroes = – 5 + = =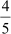

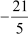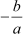
And product of zeroes = – 5 ×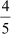 = –4 = =

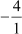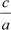
Hence, verified.

Example 2: If 1, 2, and 6 are the zeroes of the cubic polynomial x³ – 9x² + 20x – 12, then verify the relations between the zeroes and the coefficients.

Solution:

The given cubic polynomial is p(x) = x³ – 9x² + 20x – 12.

On comparing the given polynomial with the general form ax³ + bx² + cx + d of cubic polynomial, we have a = 1, b = – 9, c = 20, d = – 12.

Now the zeroes are 1, 2, and 6.

Let α = 1, β = 2 and γ = 6

Now α+ β + γ = 1 + 2 + 6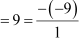

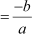
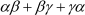= 1 × 2 + 2 × 6 + 6 × 1

= 2 + 12 + 6

= 20

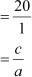
and αβ γ = 1 × 2 × 6

= 12

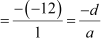
Hence, this verifies the relations between the coefficients and the zeroes of the cubic polynomial.

Formation Of Polynomial Using The Sum And Product Of Zeroes

5 and –3 are the zeroes of a quadratic polynomial p(x). Can we form the quadratic polynomial with the help of these zeroes?

Yes, we can. Let us see how we can form the polynomial.

5 is a zero of the polynomial, it means that (x – 5) is a factor of the polynomial p(x). Similarly (x + 3) is also a factor of the polynomial p(x). We know that a quadratic polynomial can have only two linear factors. Thus, we can write the polynomial p(x) as follows:

p(x) = (x – 5) (x + 3)

= x² + (– 5 + 3) x + (– 5) (3)

[Using the identity (x + a) (x + b) = x² + (a + b) x + ab, where a = – 5 and b = 3]

Thus, p(x) = x² – 2x – 15

This is the required quadratic polynomial.

If we know the zeroes of the quadratic polynomial, then we can find the polynomial as above. On the other hand, if we know the sum and product of the zeroes of the polynomial, then we can use the following formula to find the polynomial.

For example: if the sum and the product of the zeroes of a polynomial are 2 and –8 respectively, then find the polynomial.

Using the above formula, we have

p(x) = x² – (2)x + (–8)

p(x) = x² – 2x – 8

In this way, we can find the polynomial if the relationship between the zeroes is known to us.

Let us discuss some more examples based on formation of quadratic polynomial using sum and products of zeroes.

Example 1: If the sum and product of zeroes of a quadratic polynomial are 13 and 36 respectively, find the quadratic polynomial.

Solution:

Let the polynomial be p(x).

It is given that the sum of the zeroes of the polynomial = 13 and the product of the zeroes of the polynomial = 36

But we know that the quadratic polynomial p(x) in terms of sum and product of zeroes is given by the formula

p(x) = x² – (sum of zeroes)x + product of zeroes

so, we have

p(x) = x² – 13x + 36

Therefore, x² – 13x + 36 is the quadratic polynomial whose sum and the product of zeroes are 13 and 36 respectively.

Example 2: If the sum and product of zeroes of a quadratic polynomial are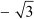 and – 6 respectively, find the quadratic polynomial.

Solution:

Let the quadratic polynomial be p(x).

It is given that the sum of the zeroes of the polynomial is 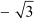and the product of the zeroes of the polynomial is – 6.

We know that the quadratic polynomial p(x) in terms of sum and product of zeroes is given by the formula

p(x) = x² – (sum of zeroes)x + product of zeroes so, we have

p(x) = x² – ( 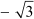)x + (– 6)

p(x) = x²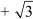 x – 6

Therefore, x²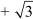 x – 6 is the quadratic polynomial whose sum and product of zeroes are 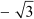and – 6 respectively.

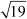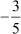Example 3: If and are the zeroes of a quadratic polynomial, then find the polynomial.

Solution:

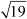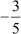Let p(x) be the required quadratic polynomial. and are the zeroes of the polynomial p(x).

Now, the sum of zeroes =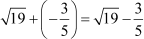

and the product of zeroes =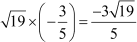

Now, the polynomial is given by the formula

p(x) = x² – (sum of zeroes)x + product of zeroes

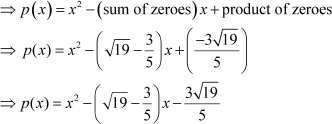
Hence, this is the required polynomial whose zeroes are 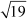and 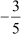respectively.