Chapter 11: Constructions

Division of a Line Segment into a Given Ratio

Vijay’s class teacher told him to mark two points A and B on a line segment PQ of length 10

cm such that 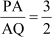and 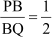. He does not know how to construct it. Can we help him? Now let us try to mark a point B in the same way.

It is given that .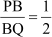

Let us take PB = x and BQ = 2x. It is also given that PQ = 10 cm.

But, PQ = PB + BQ

10 cm = x + 2x 3x = 10 cm

x =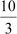 cm

Now, it is difficult to mark a point B on the line segment PQ, since the value of x is in decimal form and even non-terminating.

We can observe that the marking of point A was only possible due to two factors.

1.We were able to measure the length of AQ and PA.

2. The length of the line PQ was divisible by the sum of the numerator and denominator in the ratio 3:2 i.e., the sum of numerator and denominator is 3 + 2 = 5. The length of PQ i.e., 10 cm was divisible by 5.

But in the second example, length of PQ is not divisible by the sum of the denominator and numerator of the given ratio. In order to carry out such constructions, we follow two methods. Let us learn each of these methods with the help of examples.

Let us suppose that we have to divide a line segment of 8.8 cm in the ratio 4:7.

Let us discuss one more example to understand the concept better.

Example: Draw a line segment of length 6.2 cm and divide it in the ratio 5:3.

Solution:

To divide a line segment of length 6.2 cm in the ratio 5:3, we follow the below given steps.

1. We draw a line segment PQ of length 6.2 cm.

2. Now, we draw a ray PX making an acute angle with PQ and draw a ray QY parallel to PX by making ∠PQY equal to ∠QPX.

3.  We locate 5 points P₁, P₂, P₃, P₄, and P5 on PX and 3 points Q₁, Q₂, and Q₃ on QY such that PP₁ = P₁P₂ = P₂P₃ = P₃P₄ = P₄P₅ = QQ₁ = Q₁Q₂ = Q₂Q₃.

4. Now, we join P5Q3 which intersects PQ at R.

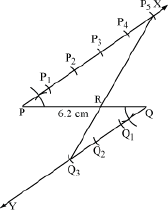
Now, R is the point on PQ which divides the line segment PQ in the ratio 5:3.

Construction Of A Triangle Similar To The Given Triangle

Consider the following triangle ABC.

In the above figure, the measures of the sides AB, BC, and CA are given as 3.8 cm, 7.9 cm, and 6.5 cm respectively.

Can we construct a triangle similar to ΔABC and whose sides are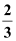 of the sides of ΔABC?

Example 1: Construct a triangle similar to the following triangle with sides 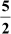of the sides of the given triangle.

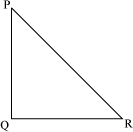
Solution:

Firstly, we draw a ray QX making an acute angle with QR on the side opposite to vertex P and mark 5 points (corresponding to the greater of 2 or 5) X1, X2, X3, X4, and X5 on QX such that QX1 = X1X2 = X2X3 = X3X4 = X4X5.

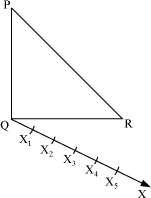
Now, we join X2R (corresponding to the denominator of the given ratio) and draw a line passing through X5 (corresponding to the numerator of the given ratio) and parallel to X2R. Let this line intersect the extended line QR at point R′. Now, we draw a line passing through R′ and parallel to RP, which intersects the extended line PQ at point P′.

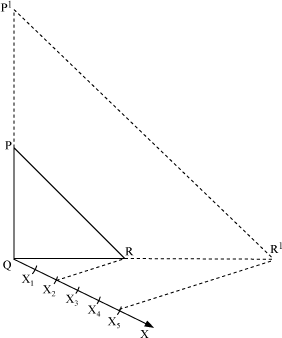
Thus, P′QR′ is the required triangle which is similar to the given triangle and with sides 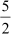of the sides of the given triangle.

Construction Of Tangents To A Circle From A Point Outside The Circle

We know that a tangent is perpendicular to the radius through the point of contact. Therefore, if we want to draw a tangent at a point of a circle, we have to simply draw the radius through that point and draw a line perpendicular to that radius. It will be the required tangent at that point.

However, we do not follow this method, when a point lies outside the circle. This is because we do not know at which point on the circle the radius should be drawn so that the line joining that point and the point outside the circle is perpendicular to the radius.

Example 1: Draw a pair of tangents to a circle of radius 4 cm from a point outside the circle such that the tangents are inclined at an angle of 70°.

Solution:

We can draw the tangents using a property of circles. It is given that the tangents are inclined at an angle of 70°. Therefore, the radii joining the points of contacts to the centre of the circle are inclined at an angle of 110° as shown in the figure.

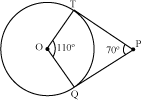
Firstly, let us draw a circle of radius 4 cm with the help of ruler and compasses. Let O be the centre of the circle.

We draw a radius OT of the circle. Now we draw another radius OQ making an angle of 110° with OT.

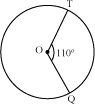
Now, we draw lines perpendicular to OT and OQ at points T and Q respectively. Let these two perpendicular lines intersect each other at a point P.

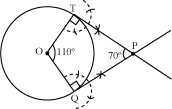
Thus, PT and PQ are the required tangents that are inclined at an angle of 70°.

Example 2: Draw a pair of tangents from point P to the given circle.

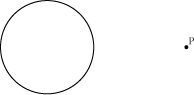
Solution:

In the given figure, the centre of the circle is not given. Therefore, first of all, we will find the centre of the circle.

For this, let us draw two non-parallel chords of the circle and draw their perpendicular bisectors. The point of intersection of these perpendicular bisectors is the centre O of the circle.

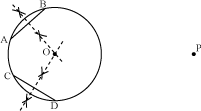
Now, we join the line segment OP and draw its perpendicular bisector. Let this perpendicular bisector intersect OP at point M.

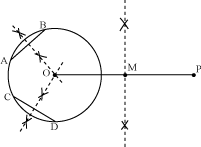
Then we draw a circle with radius equal to OM taking M as centre. Let this circle intersect the given circle at points T and Q. We join PT and PQ.

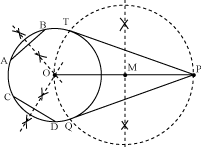
Thus, PT and PQ are the required tangents from a point P outside the circle.