Distance and displacement, velocity;
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Distance and Displacement
Distance -The actual path or length travelled by the object travelled by the object is called the distance.
It is a scalar quantity.
It is always positive.
It can never be zero or negative.
Displacement – It is the shortest path between initial and final point.
It is a vector quantity.
It can be positive or negative.
It can be zero.
Difference bw distance and displacement
Example 1: A body travels in a semicircular path of radius 10 m starting its motion from point ‘A’ to point ‘B’. Calculate the distance and displacement.
Example 2: A body travels 4 km towards North then he turn to his right and travels another 4 km before coming to rest. Calculate (i) total distance travelled, (ii) total displacement.
Velocity - It is defined as the displacement of the body per unit time.
Velocity = displacement travelled / time taken
SI unit = m/s (meter/second)
Average Velocity - The average velocity of a body is the total displacement travelled by the total time taken to cover this distance.
Average velocity= Total Displacement/Total Time taken
Avg. Velocity (vavg) = (Initial velocity + Final velocity)/2 = (u+v)/2
where, u = initial velocity, v = final velocity
Example 1: During first half of a journey by a body it travel with a speed of 40 km/hr and in the next half it travels with a speed of 20 km/hr. Calculate the average speed of the whole journey.
Example 2 : If Ananya was able to travel 6 km in North in 2 hour in his car. What was her velocity?
Example 3: A car travels 20 km in first hour, 40 km in second hour and 30 km in third hour. Calculate the average speed of the train.
Force and Motion,
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
→ Force: It is the force that enables us to do any work. To do anything, either we pull or push the object. Therefore, pull or push is called force.
Example, to open a door, either we push or pull it. A drawer is pulled to open and pushed to close.
Effects of Force
→ Force can make a stationary body in object.
For example: a football can be set to move by kicking it i.e. by applying a force.
→ Force can stop a moving body. For example, by applying brakes, a running cycle or a running vehicle can be stopped.
→ Force can change the direction of a moving object.
For example: by applying force i.e. by moving handle, the direction of a running bicycle can be changed. Similarly by moving steering, the direction of a running vehicle is changed.
→ Force can change the speed of a moving body. By accelerating, the speed of a running vehicle can be increased or by applying brakes the speed of a running vehicle can be decreased.
→ Force can change the shape and size of an object.
For example: by hammering, a block of metal can be turned into a thin sheet. By hammering, a stone can be broken into pieces.
• Forces are mainly of two types:
(i) Balanced forces
(ii) Unbalanced forces
Balanced Forces
→ If the resultant of applied forces is equal to zero, it is called balanced forces.
Example: In the tug of war if both the team apply similar magnitude of forces in opposite directions, rope does not move in either side.
This happens because of balanced forces in which resultant of applied forces become zero.
→ Balanced forces do not cause any change of state of an object. Balanced forces are equal in magnitude and opposite in direction.
→ Balanced forces can change the shape and size of an object.
For example: When forces are applied from both sides over a balloon, the size and shape of balloon is changed.
Unbalanced Forces
→ If the resultant of applied forces are greater than zero, the forces are called unbalanced forces.
→ An object in rest can be moved because of applying balanced forces.
• Effects of Unbalanced forces -
→ Move a stationary object
→ Increase the speed of a moving object
→ Decrease the speed of a moving object
→ Stop a moving object
→ Change the shape and size of an object
Laws of Motion
• Galileo Galilei: Galileo first of all said that object move with a constant speed when no forces act on them.
→ This means if an object is moving on a frictionless path and no other force is acting upon it, the object would be moving forever. That is, there is no unbalanced force working on the object. But practically it is not possible for any object.
→ Force of friction, force of air and many other forces are always acting upon an object.
Gravitation;
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Introduction
→ Gravitational Force of Earth: If we release a small stone without pushing it from a height, it accelerates towards earth. Earth attracts everything towards it by an unseen force of attraction. This force of attraction is known as gravitation or gravitational pull
Thrust and pressure.
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Thrust and Pressure
Force acting on an object perpendicular to the surface is called thrust.
Effect of thrust depends on the area of contact.
The pressure is thrust per unit area.
SI unit is the pascal (Pa).
Force acting on a smaller area applies more pressure than the same force acting on a larger area.
• Pressure depends on two factors
(i) Force applied
(ii) Area of surface over which force acts
Examples of Pressure
→ The base of high buildings is made wider so that weight of walls act over a large surface are
pressure is less.
→ School bags are having broad strap so that the weight of school bags fall over a larger area so that student feel less pressure on shoulders.
--> liquids and gases are fluids and they exert pressure in all directions.
Work done by a force, energy, power;
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Introduction
→ The energy for the ‘life processes’ comes from food. Activities like playing, singing, reading, w
thinking, jumping, cycling and running requires energy.
Work
Work done on an object is defined as the product of the magnitude of the force acting on the body and the displacement in the direction of the force.
W = F.s
If a force acting on a body causes no displacement, the work done is 0. For example, pushing a wall.
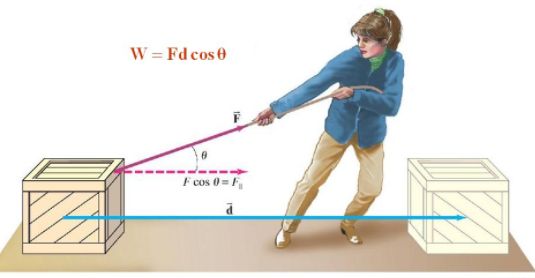
Two conditions need to be satisfied for work to be done:
(i) A force should act on object
(a) The object must be displaced
Work = Force x Displacement
Unit of workdone = Joule = Newton x metre
1 Joule work is said to be done when 1 Newton force is applied on an object and it shows the displacement by 1 meter.

Energy
Energy is defined as the ability to do work. Its unit is the same as that of work.
SI unit of energy or work = Joule (Nm)
Energy has different forms: Light, heat, chemical, electrical or mechanical.
Mechanical energy is the sum of:
(i) Kinetic energy (K.E)
(ii) Potential energy (P.E)
Power
The rate of doing work or the rate of transfer of energy is called power. It is denoted by P
⇒ P = Wt
SI unit is Watt (J/s).
Average power = Total energy consumed / Total time taken
The commercial unit of power is kWh i.e. energy used in 1 hour at 1000 Joules/second.
1KWh = 3.6×106 J
Nature of sound and its propagation in various media, speed of sound,
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Introduction
→ The sensation felt by our ears is called sound.
→ Sound is a form of energy which makes us hear.
→ Law of conservation of energy is also applicable to sound.
→ Sound travels in form of wave.
Production of Sound
→ Sound is produced when object vibrates or sound is produced by vibrating objects.
→ The energy required to make an object vibrate and produce sound is provided by some out
source (like our hand, wind etc.).
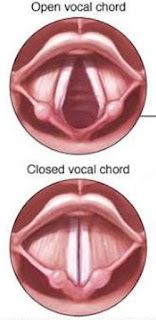
→ Example: Sound of our voice is produced by vibration of two vocal cords in our throat.
• Sound of a drum or tabla is produced by vibration of its membrane
when struck.
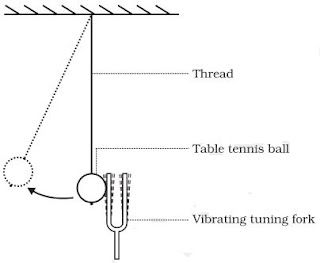
→ In laboratory experiments, sound is produced by vibrating tuning fork. The vibrations of tuning fork
can be shown by touching a small suspended pith ball (cork ball) with a prong of the sounding
tuning fork. The pith ball is pushed away with a great force.

→ In laboratory experiments, sound is produced by vibrating tuning fork. The vibrations of tuning fork
can be shown by touching a small suspended pith ball (cork ball) with a prong of the sounding
tuning fork. The pith ball is pushed away with a great force.
• Sound can be produced by following methods:
(i) By vibrating string (sitar)
(ii) By vibrating air (flute)
(iii) By vibrating membrane (table, drum)
(iv) By vibrating plates (bicycle bell)
(v) By friction in objects
(vi) By scratching or scrubbing the objects etc.
Propogation of Sound
→ The substance through which sound travels is called a medium.
→ The medium may be solid, liquid or gas.
→ When an object vibrates, then the air particles around it also start vibrating in exactly the same
way and displaced from their stable position.
→ These vibrating air particles exert a force on nearby air particles so they are also displaced from
their rest position and start to vibrate.
→ This process is continued in the medium till sound reaches our ears.
→ The disturbance produced by sound travels through the medium (not the particles of the
medium).
→ Wave is a disturbance which travels through a medium and carries energy.
→ So sound travels in wave form known as mechanical waves.
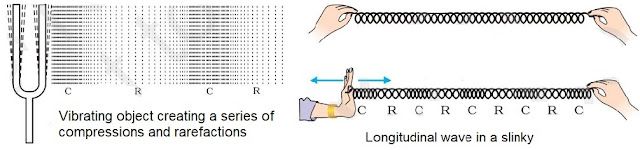
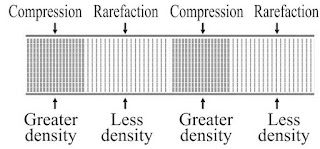
• When a body vibrates then it compresses the air surrounding it and form a area of high density
called compression (C).
→ Compression is the part of wave in which particles of the medium are closer to one another
forming high pressure.
→ This compression move away from the vibrating body.
• When vibrating body vibrates back a area of low pressure is formed called rarefaction (R).
→ Rarefaction is the area of wave in which particles of the medium are further apart from one
another forming a low pressure or low density area.
→ When body vibrates back and forth, a series of compression and rarefaction is formed in air
resulting in sound wave.
→ Propogation of sound wave is propogation of density change.
Sound needs Medium for Propogation
• Sound waves are mechanical waves.
→ It needs material medium for propogation like air, water, steel etc.
→ It cannot travel in vaccum.
→ An electric bell is suspended in airtight bell jar connected with vacuum pump.
→ So, medium is necessary for propagation of sound.
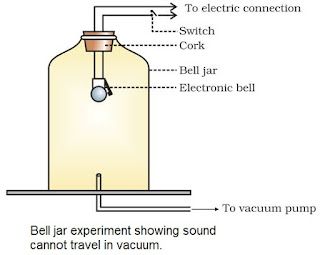
Experiment to show that sound cannot travel through vacuum
Sound Waves as Longitudinal Waves
• A wave in which the particles of the medium vibrate back and forth in the same direction in which
the wave is moving, is called a longitudinal wave.
→ When we push and pull the slinky compression (number of turns are more or closer) and
rarefaction (number of turns are less or farther) are formed.
→ When a wave travels along with slinky, its each turn moves back and forth by only a small
distance in the direction of wave. So the wave is longitudinal.
→ The direction of vibrations of the particles is parallel to the direction of wave.

• When one end of a slinky is moved up and down rapidly whose other end is fixed, it produces
transverse wave.
→ This wave possess along the slinky in horizontal direction, while turns of slinky (particles) vibrates
up and down at right angle to the direction of wave.
→ Thus in transverse wave particles of the medium vibrate up and down at right angles to the
direction of wave.
→ Light waves are transverse waves but they don’t need a material
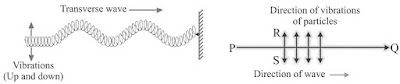
Characteristics of Sound Wave
• The characteristics of sound waves are : wavelength, frequency, amplitude, time period and
velocity.
→ When a wave travel in air the density and pressure of air changes from their mean position.
→ Compression is shown by crest while rarefaction is shown by trough.
→ Compression is the region of maximum density or pressure.
→ Rarefaction is the region of minimum density or pressure.
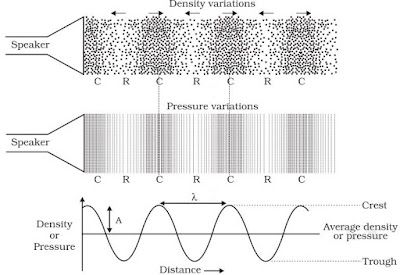
Wavelength
→ In sound waves the combined length of a compression and an adjacent rarefaction is called
wavelength.
→ The distance between the centres of two consecutive compressions or two consecutive
rarefactions is also called its wavelength.
→ It is denoted by the Greek letter lamda (λ). Its SI unit is metre.
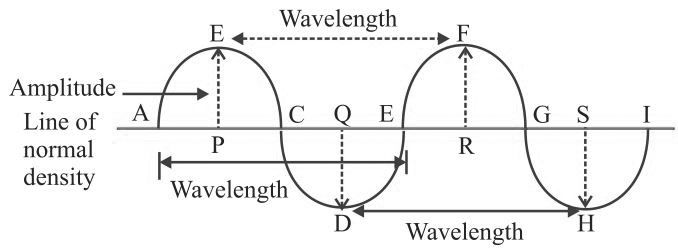
Frequency
→ No. of complete waves produced in one second or number of vibrations per second is called
frequency.
→ Number of compressions or rarefactions passed in one second is also frequency.
→ Frequency of wave is same as the frequency of the vibrating body which produces the wave
• The SI unit of frequency is hertz (Hz). The symbol of frequency is v (nu).
• 1 Hertz: One Hz is equal to 1 vibration per second.
• Bigger unit of frequency is kilohertz kHz = 1000 Hz.
Time Period
→ Time taken to complete one vibration is called time period.
→ Time required to pass two consecutive compressions or rarefactions through a point is called
time period.
• SI unit of time period is second (s). Time period is denoted by T.
• The frequency of a wave is the reciprocal of the time period.
• v = 1/T
Amplitude
→ The maximum displacement of the particle of the medium from their original undisturbed
position is called amplitude of the wave.
• Amplitude is denoted by A and its SI unit is metre (m).
→ Sound have characteristics like pitch and loudness and timbre.
• Pitch: The pitch of sound depends on the frequency of sound (vibration).
→ It is directly proportional to its frequency. Greater the frequency, higher is the pitch and lesser the
frequency, lower is the pitch.
→ A woman’s voice is shrill having a high pitch while a man’s voice is flat having low pitch.
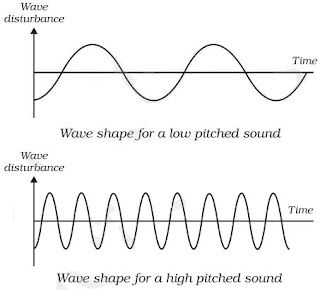
• Loudness: The loudness depends on the amplitude of the sound wave.
→ Loudness is the measure of the sound energy reaching the ear per sec.
→ Greater the amplitude of sound wave, greater is the energy, louder the sound; short is the
amplitude, less is the energy, soft is the sound.
→ Loudness is measured in decibel ‘dB’.
• Quality or Timbre: The timbre of a sound depends on the shape of sound wave produced by
the characteristic of musical sound.
→ It helps us to distinguish between two sounds of same pitch & loudness.
• Sound of single (same) frequency is called tone while a mixture of different frequencies is called
note.
• The distance travelled by a wave in one second is called velocity of the wave.
• Its SI unit is metre per second (m/s ).
Velocity = Distance travelled/Time taken
⇒ v = λ/T
(λ is the wavelength of the waves travelled in one time time period T)
v = λv (1/T = v)
So, Velocity = Wavelength × Frequency
This is the wave equation.
Example: What is the frequency of sound wave whose time period is 0.05 second ?
Speed of Sound in Various Mediums
→ Speed of sound depends on the nature of material through which it travels. It is slowest in gases,
faster in liquids and fastest in solids.
→ Speed of sound increases with the rise in temperature.
→ Speed of sound increases as humidity of air increases.
→ Speed of light is faster than speed of sound.
→ In air, speed of sound is 344 ms -1 at 22ºC.
Sonic Boom
→ Some aircrafts, bullets, rockets etc. have ‘supersonic speed’.
• Supersonic refers to the speed of an object which is greater than the speed of sound and it
produces extremely loud sound waves called ‘shock waves’ in air.
uniform and non-uniform motion along a straight line
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Uniform Motion and Non-uniform Motion
Uniform motion - When a body covers equal distances in equal intervals of time then the body is said to describe uniform motion.
Non uniform motion - When a body moves unequal distances in equal intervals of time or vice-versa, then the body is said to describe non-uniform motion.

acceleration
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Acceleration -
Acceleration is seen in non-uniform motion and it can be defined as the rate of change of velocity with time.
Acceleration (a) = Change in velocity/Time = (v-u)/t
where, v = final velocity, u = initial velocity
If v > u, then ‘a’ will be positive (+ve).
Retardation/Deceleration -
Deceleration is seen in non-uniform motion during decrease in velocity with time. It has same definition as acceleration
Deceleration (a') = Change in velocity/Time = (v-u)/t
Here, v < u, ‘a’ = negative (-ve).
It is a vector quantity.
SI unit – m/s2 ( meter per second square)
Example 1: A car speed increases from 40 km/hr to 60 km/hr in 5 sec. Calculate the acceleration of car.
Example 2: A car travelling with a speed of 20 km/hr comes into rest in 0.5 hrs. What will be the valu of its retardation?
EXAMPLE 3 : If the velocity of the car reduced to 80 m/s from 120 m/s in 8 seconds on applying breaks . Calculate its acceleration
distance-time and velocity-time graphs for uniform motion and uniformly accelerated motion
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Uniform Acceleration - If the change in velocity in equal intervals of time is always the same, then the object is said to be moving with uniform acceleration.
Example: a body falling from a height towards the surface of the earth.
Non-uniform or Variable Acceleration- If the change in velocity in equal intervals of time is not the same, then the object is said to be moving with variable acceleration.
Example - A ball thrown vertically upwards is moving with a negative acceleration as the velocity decreases with time.
Graphs for Motion -
1) Distance-time graphs (s-t graphs)
a) When the object is stationary or at rest -
The distance time graph for stationary object is the line parallel to time axis.
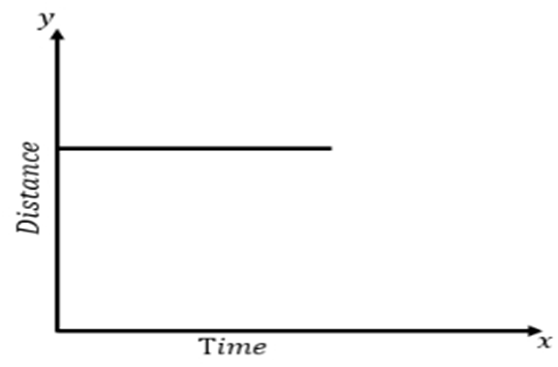
b) When object is in uniform motion -
The distance time graph for the object moving in uniform motion is the straight line inclined to time axis
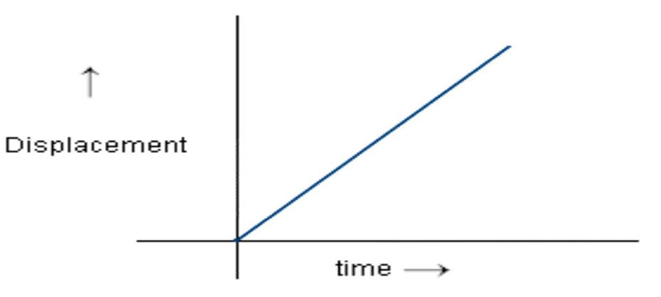
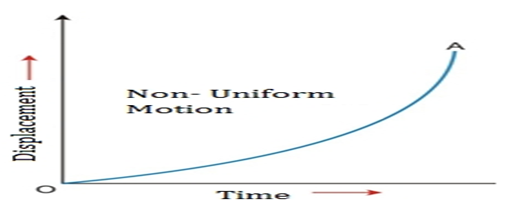
C) When object is in non-uniform motion -
The distance time graph for object moving in non -uniform motion is the curved line.
Important results of distance time graphs -
1) area under curve of s-t graph = displacement/distance travelled by the object
2) slope of s-t graph = velocity of the object
equations of motion by graphical method
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Definition of Equations of Motion
Equations of motion, in physics, are defined as equations that describe the behaviour of a physical system in terms of its motion as a function of time.
There are three equations of motion that can be used to derive components such as displacement(s), velocity (initial and final), time(t) and acceleration(a). The following are the three equation of motion:
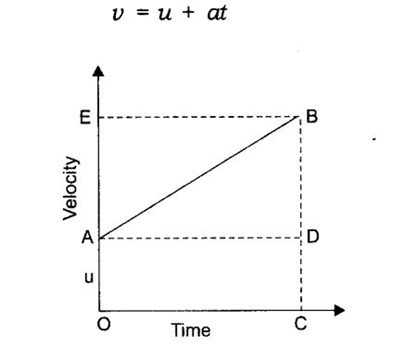
First Equation of Motion : v=u+at
Second Equation of Motion : s=ut+1/2 at2
Third Equation of Motion : v2=u2+2as
DERIVATION OF FIRST EQUATION OF MOTION ( V = u+at )
Consider a body of mass “m” having initial velocity “u”. Let after time “t” its final velocity becomes “v” due to uniform acceleration “a”.
Now as we know that,
Acceleration = change in velocity/Time taken Acceleration = Final velocity-Initial velocity / time taken
a = v-u/t
=> at = v-u
or v = u + at
This is the first equation of motion.
DERIVATION OF SECOND EQUATION OF MOTION (S=ut+1/2 at2 )
Consider a body of mass “m” having initial velocity “u”. Let after time “t” its final velocity becomes “v” due to uniform acceleration “a”. Let the distance travelled by the body be “s”.
Now As we know that,
Distance = Average velocity X Time
Also, Average velocity = u+v/2
Distance (s) = ( u+v ) *t/2 …….eq.(1)
Again we know that, v = u + at
By substituting this value of “v” in eq.(1), we get
Distance(s) = (u+u+at) *t/2
=> s = (2u+at)* t/2
=> s = 2ut/2+at2/2
=>s = ut+ at2/2
or s = ut + 1/2 at2
This is the second equation of motion.
DERIVATION OF THIRD EQUATION OF MOTION (V2 = u2+2as)
Consider a body of mass “m” having initial velocity “u”. Let after time “t” its final velocity becomes “v” due to uniform acceleration “a”. Let the distance travelled by body be “s”.
Displacement=(Initial Velocity+Final Velocity)×t/2
Substituting the standard notations, the above equation becomes
s=(u+v)×t/2
From the first equation of motion, we know that
v=u+at
Rearranging the above formula, we get
t=v−u/a
Substituting the value of ‘t’ in the displacement formula, we get
s=(v+u)/2 *(v−u)/a
s=(v2 - u2)/2a
2as= v2 - u2
Rearranging, we get
v2 – u2= 2as
This is the third equation of motion.
elementary idea of uniform circular motion.
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Introduction To Uniform Circular Motion
We have come across different types of motions in our previous sessions. Rotatory motion, rectilinear motion, oscillatory motion, uniform circular, and periodic motion are some types of motion. Movement of an object while rotating along a circular path is known as circular motion. Circular motion can be either uniform or non-uniform. In this article, let us discuss in brief the uniform circular motion along with examples.
What is Uniform Circular Motion?
The movement of a body following a circular path is called a circular motion. Now, the motion of a body moving with constant speed along a circular path is called Uniform Circular Motion. Here, the speed is constant but the velocity changes.
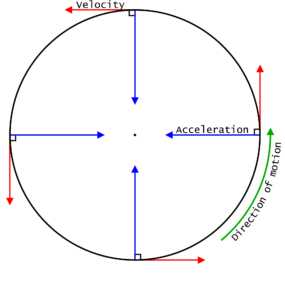
NOTE -
So if a particle is moving in a uniform circular motion:
Its speed is constant
Velocity is changing at every instant
Uniform Circular Motion Examples
Following are the examples of uniform circular motion:
Motion of artificial satellites around the earth is an example of uniform circular motion. The gravitational force from the earth makes the satellites stay in the circular orbit around the earth.
The motion of electrons around its nucleus.
The motion of blades of the windmills.
The tip of second’s hand of a watch with circular dial shows uniform circular motion.
Formula for velocity in UCM -
V=2πR/T
where R is radius of circle, T is time taken
Newton’s Laws of Motion
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Newton’s Laws of Motion
→ Newton studied the ideas of Galileo and gave the three laws of motion. These laws are known as Newton’s laws of motion.
Newton’s First Law of Motion (Law of Inertia)
→ Any object remains in the state of rest or in uniform motion along a straight line, until it is compelled to change the state by applying external force.
Explanation: If any object is in the state of rest, then it will remain in rest until a external force is applied to change its state. Similarly, an object will remain in motion until any external force is applied over it to change its state.
This means all objects resist to in changing their state. The state of any object can be changed by applying external forces only, this property is called inertia.
• Newton’s First Law of Motion in Everyday Life
(i) A person standing in a bus falls backward when bus starts moving suddenly.
→ This happens because the person and bus both are in rest while bus is not moving, but as the bus starts moving, the legs of the person start moving along with bus but rest portion of his body has the tendency to remain in rest. Because of this, the person falls backward; if he is not alert.
(ii) A person standing in a moving bus falls forward if driver applies brakes suddenly.
→ This happens because when bus is moving, the person standing in it is also in motion along with bus. But when driver applies brakes the speed of bus decreases suddenly or bus comes in the state of rest suddenly, in this condition the legs of the person which are in contact with the bus come in rest while the rest part of his body have the tendency to remain in motion. Because of this person falls forward if he is not alert.
(iii) Before hanging the wet clothes over laundry line, usually many jerks are given to the clothes to get them dried quickly. Because of jerks, droplets of water from the pores of the cloth falls on the ground and reduced amount of water in clothes dries them quickly.
→ This happens because when suddenly clothes are made in motion by giving jerks, the water droplets in it have the tendency to remain in rest and they are separated from clothes and fall on the ground.
(iv) When the pile of coin on the carom-board is hit by a striker, coin only at the bottom moves away leaving rest of the pile of coin at same place.
→ This happens because when the pile is struck with a striker, the coin at the bottom comes in motion while rest of the coin in the pile has the tendency to remain in the rest and they vertically falls the carom-board and remain at same place.
Statement of Second Law of Motion
→ Rate of change of momentum of an object is proportional to applied unbalanced force in the direction of force.
Mathematical expression
Suppose, Mass of an object = m kg
Initial velocity of an object = u m/s
Final velocity of an object = v m/s
∴ Initial momentum, p1 = mu
Final momentum, p2 = mv
∴ Change in momentum = Final momentum – Initial momentum
= mv – mu
= m(v – u)
∴ Rate of change of momentum = Change in momentum/Time taken
= m(v-u)/t
• According to 2nd law, this rate of change is momentum is directly proportional to force.
We know that, a = (v-u)/t (From 1st equation of motion)
∴ F = kma
where, k is a constant. Its value can be assumed as 1.
∴ F = 1 × m × a = ma
• SI unit = kg m/s2 or Newton
1 Newton: When an acceleration of 1 m/s2 is seen in a body of mass 1 kg, then the
force applied on the body is said to be 1 Newton.
Proof of Newton’s First Law of Motion from Second Law
→ First law states that if external force F = 0, then a moving body keeps moving with the same velocity, or a body at rest continues to be at rest.
∴ F = 0
We know, F = m(v-u)/t
(i) A body is moving with initial velocity u then,
m(v-u)/t = 0 ⇒ v – u = 0
∴ v = u
Thus, final velocity is also same.
(ii) A body is at rest i.e., u = 0
Therefore, from above u = v = 0
So, the body will continue to be at rest.
Third Law of Motion
→ For every action there is an equal an opposite reaction.
Applications
(i) Walking is enabled by 3rd law.
(ii) A boat moves back when we deboard it.
(iii) A gun recoils.
(iv) Rowing of a boat.
Action and reaction forces
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Third Law of Motion
→ For every action there is an equal an opposite reaction.
Applications
(i) Walking is enabled by 3rd law.
(ii) A boat moves back when we deboard it.
(iii) A gun recoils.
(iv) Rowing of a boat.
Inertia of a body
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
→ The property of an object because of which it resists to get disturb its state is called inertia.
Inertia and mass
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Mass and Inertia
→ The property of an object because of which it resists to get disturb its state is called inertia.
→ Inertia of an object is measured by its mass. Inertia is directly proportional to the mass. This means inertia increases with increase in mass and decreases with decrease in mass.
→ A heavy object will have more inertia than the lighter one. In other words, the natural tendency of an object that resists the change in state of motion or rest of the object is called inertia.
→ Since a heavy object has more inertia, thus it is difficult to push or pull a heavy box over the ground than the lighter one.
Momentum
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Momentum
→ Momentum is the power of motion of an object.
→ The product of velocity and mass is called the momentum. Momentum is denoted by ‘p’.
→ Therefore, Momentum of the object = Mass × Velocity (p = m × v)
where, p = momentum, m = mass of the object and v = velocity of the object.
• Some explanations to understand the momentum:
→ A person get injured in the case of hitting by a moving object, such as stone, pebbles or anything because of momentum of the object.
→ Even a small bullet is able to kill a person when it is fired from a gun because of its momentum due to great velocity.
→ A person get injured severely when hit by a moving vehicle because of momentum of vehicle due to mass and velocity.
Momentum and Mass
→ Since momentum is the product of mass and velocity (p = m × v) of an object. This means momentum is directly proportional to mass and velocity. Momentum increases with increase of either mass or velocity of an object.
→ This means if a lighter and a heavier object is moving with same velocity, then heavier object will have more momentum than the lighter one.
→ If a small object is moving with great velocity, it has tremendous momentum. And because of momentum, it can harm an object more severely.
Example: a small bullet having a little mass even kills a person when it is fired from a gun.
→ Usually, road accidents prove more fatal because of high speed than in slower speed. This happens because vehicles running with high speed have greater momentum compared to a vehicle running with slower speed.
Momentum of an object which is in the state of rest
Let an object with mass ‘m’ is in the rest.
Since, object is in rest, therefore, its velocity, v = 0
Now we know that,
Momentum = mass × velocity
⇒ p = m × 0 = 0
Thus, the momentum of an object in the rest i.e. non-moving, is equal to zero.
Unit of momentum
→ SI unit of mass = kg
→ SI unit of velocity = m/s
We know that,
Momentum (p) = m × v
∴ p = kg × m/s ⇒ p = kg m/s
Numerical Problems Based on Momentum
Type I: Calculation of Momentum
Example 1: What will be the momentum of a stone having mass of 10 kg when it is thrown with a velocity of 2 m/s?
Solution
Mass (m) = 10 kg
Velocity (v) = 2 m/s
We know that,
Momentum (p) = Mass (m) × Velocity (v)
∴ p = 10 kg × 2 m/s = 20 kg m/s
Thus, the momentum of the stone = 20 kg m/s.
Example 2: Calculate the momentum of a bullet of 25 g when it is fired from a gun with a velocity of 100 m/s.
Solution
Given, Velocity of the bullet (v) = 100 m/s
Mass of the bullet (m) = 25 g = 25/1000 kg = 0.025 kg
Since, p = m × v
∴ p = 0.025 × 100 = 2.5 kg m/s
Momentum of the bullet = 2.5 kg m/s.
Example 3: Calculate the momentum of a bullet having mass of 25 g is thrown using hand with a velocity of 0.1 m/s.
Solution
Given, Velocity of the bullet (v) = 0.1 m/s
Mass of the bullet (m) = 25 g = 25/1000 kg = 0.025 kg
Momentum (p) = Mass (m) × Velocity (v)
∴ p = 0.025 kg × 0.1 m/s
⇒ p = 0.0025 kg m/s
Momentum of the bullet = 0.0025 kg m/s.
Example 4: The mass of a goods lorry is 4000 kg and the mass of goods loaded on it is 20000 kg. If the lorry is moving with a velocity of 2 m/s, what will be its momentum?
Solution
Given, Velocity (v) = 2 m/s
Mass of lorry = 4000 kg
Mass of goods on the lorry = 20000 kg
∴ Total mass (m) on the lorry = 4000 kg + 20000 kg = 24000 kg
Momentum (p) = Mass (m) × Velocity (v)
∴ p = 24000 kg × 2 m/s
⇒ p = 48000 kg m/s
Momentum of the lorry = 48000 kg m/s.
Example 5: A car having mass of 1000 kg is moving with a velocity of 0.5 m/s. What will be its momentum?
Solution
Given, Velocity of the car (v) = 0.5 m/s
Mass of the car (m) = 1000 kg
Momentum (p) = Mass (m) × Velocity (v)
∴ p = 1000 kg × 0.5 m/s = 500 kg m/s
Momentum of the car = 500 kg m/s.
Force and Acceleration
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
→ Force:
It is the force that enables us to do any work. To do anything, either we pull or push the object. Therefore, pull or push is called force.
Example, to open a door, either we push or pull it. A drawer is pulled to open and pushed to close.
Elementary idea of conservation of Momentum
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Law of Conservation of Momentum
→ When two (or more) bodies act upon one another, their total momentum remains constant (or conserved) provided no external forces are acting.
• Initial momentum = Final momentum
Suppose, two objects A and B each of mass m1 and mass m2 are moving initially with velocities u1 and u2, strike each other after time t and start moving with velocities v1 and v2 respectively.
Now, Initial momentum of object A = m1u1
Initial momentum of object B = m2u2
Final momentum of object A = m1v1
Final momentum of object B = m2v2
So, Rate of change of momentum in A,
F1 = (m1v1 - m1u1)t = m1(v1 - u1)/t ....(i)
Rate of change of momentum in B,
F2 = (m2v2 – m2u2)t = m2(v2 - u2)/t ....(ii)
We know from 3rd law of motion,
F1 = −F2
So, m1(v1 - u1)/t = - m2(v2 - u2)/t
⇒ m1v1 – m1u1 = -m2v2 + m2u2
⇒ m1u1 + m2u2 = m1v1 + m2v2
Thus, Initial momentum = Final momentum
Example 1: A bullet of mass 20 g is fired horizontally with a velocity of 150 m/s from a pistol of mass 2 kg. Find the recoil velocity of the pistol.
Solution
Given, Mass (m1) of bullet = 20 g = 0.02 kg
Mass (m2) of pistol = 2 kg
Initially bullet is inside the gun and it is not moving.
∵ Mass = m1+m2 = (0.02 + 2) kg = 2.02 kg
and u1 = 0
∴ Initial momentum = 2.02 × 0 = 0 ....(i)
Let the velocity of pistol be v2 and v1 for bullet = 150
∴ Final momentum = m1v1 + m2v2 = 0.02×150 + 2v2 ...(ii)
We know that,
Initial momentum = Final momentum
∴ (0.02×150)/100 + 2v2 = 0 [From equations (i) and (ii)]
⇒ 3 + 2v2 = 0
⇒ 2v2 = −3
⇒ v2 = −1.5 m/s
(−)ve sign indicates that gun recoils in direction opposite to that of the bullet.
Example 2: Two hockey players viz A of mass 50 kg is moving with a velocity of 4 m/s and another one B belonging to opposite team with mass 60 kg is moving with 3 m/s, get entangled while chasing and fall down. Find the velocity with which they fall down and in which direction?
Solution
Given,
mA = 50 kg, uA = 4 m/s
mB = 60 kg, uB = 3 m/s
Initial momentum A = mAuA = 50 × 4 = 200 kgm/s
Initial momentum B = MBuB = 60 × 3 = 180 kgm/s
∴ Total initial momentum = 200 + 180 = 380 kgm/s ....(i)
Final momentum = (mA + mB)v = (50 + 60)v = 110v ....(ii)
According to the law of conservation of momentum,
380 = 110v
⇒ v = 380/110 = 3.454 m/s
universal law of gravitation
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Universal Law of Gravitation
→ Sir Isaac Newton in 1687 proposed a law about the force of attraction between the
objects in the universe which is known as Newton’s law of gravitation.
According to Universal law of Gravitation
→ Every mass in this universe attracts every other mass with a force which is directly proportional to
the product of two masses and inversely proportional to the square of the distance between them
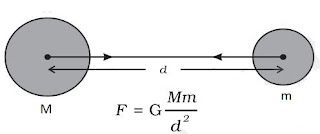
• Let masses (M) and (m) of two objects are distance (d) apart, then force of attraction (F) between
them
F ∝ M×m
F ∝ 1/d2
F ∝ Mm/d2
F = (GMm)/d2
where,
G is a constant and is known as Gravitational constant.
Value of G = 6.67×10-11 Nm2/kg2
G is called universal gravitational constant.
→ If unit of F is in Newton, m is in kg, d is in mere, then unit of G can be calculated as :
G = (F×d2)/Mm, therefor unit will be Nm2/kg2
Importance of universal law of gravitation
(i) The force that binds us to the earth.
(ii) The motion of moon around the earth.
(iii) The motion of earth around the sun.
(iv) The tides due to moon and the sun.
force of gravitation of the earth (gravity)
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Free fall of an object and acceleration (g)
→ When an object is thrown upward, it reaches certain height, then it starts falling down towar
earth. It is because the earth’s gravitational force exerts on it.
→ This fall under the influence of earth is called ‘free fall of an object’.
→ During this free fall direction do not change but velocity continuously changes which is calle
acceleration due to gravity. It is denoted by ‘g’.
→ Its unit is same as acceleration m/s .
acceleration due to gravity
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Gravitational Acceleration and its value at the surface of earth
→ The uniform acceleration produced in a freely falling object due to the gravitational force of
earth, is called acceleration due to gravity.
→ It is represented by ‘g’ and it always acts towards the centre of the earth.
Mathematical Expression for g
From the second law of motion, force is the product of mass and acceleration.
F = ma
For free fall, acceleration is replaced by acceleration due to gravity.
Therefore, force becomes:
F = mg ….(i)
But from Universal Law of Gravitation,
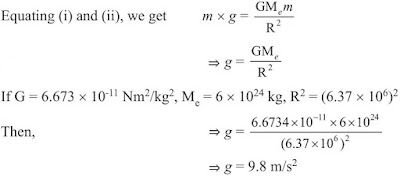
Factors Affecting the Value of g
- As the radius of the earth increases from the poles to the equator, the value of g becomes greater at the poles than at the equator.
- As we go at large heights, value of g decreases.
To Calculate the Value of g
Value of universal gravitational constant, G = 6.7 × 10–11 N m2/ kg2,
Mass of the earth, M = 6 × 1024 kg, and
Radius of the earth, R = 6.4 × 106 m
Putting all these values in equation (iii), we get:
![]()
Thus, the value of acceleration due to gravity of the earth, g = 9.8 m/s2.
Difference between Gravitation Constant (G) and Gravitational Acceleration (g)

Motion of Objects Under the Influence of Gravitational Force of the Earth
Let an object is falling towards earth with initial velocity u. Let its velocity, under the effect of gravitational acceleration g, changes to v after covering the height h in time t.
Then the three equations of motion can be represented as:
Velocity (v) after t seconds, v = u + ght
Height covered in t seconds, h = ut + ½gt2
Relation between v and u excluding t, v2 = u2 + 2gh
The value of g is taken as positive in case of the object is moving towards earth and taken as negative in case of the object is thrown in opposite direction of the earth.
mass and weight
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Mass & weight
Mass (m)
- The mass of a body is the quantity of matter contained in it.
- Mass is a scalar quantity which has only magnitude but no direction.
- Mass of a body always remains constant and does not change from place to place.
- SI unit of mass is kilogram (kg).
- Mass of a body can never be zero.
Weight (W)
- The force with which an object is attracted towards the centre of the earth, is called the weight of the object.
Now, Force =m×a
But in case of earth,a=g
∴F=m×g
But the force of attraction of earth on an object is called its weight (W).
∴W=mg - As weight always acts vertically downwards, therefore, weight has both magnitude and direction and thus it is a vector quantity.
- The weight of a body changes from place to place, depending on mass of object.
- The SI unit of weight is Newton.
- Weight of the object becomes zero if g is zero.
Weight of an Object on the Surface of Moon
Mass of an object is same on earth as well as on moon. But weight is different.
weight of the object on the moon = (1/6) × its weight on the earth.
free fall
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Free fall of an object and acceleration (g)
→ When an object is thrown upward, it reaches certain height, then it starts falling down towar
earth. It is because the earth’s gravitational force exerts on it.
→ This fall under the influence of earth is called ‘free fall of an object’.
→ During this free fall direction do not change but velocity continuously changes which is calle
acceleration due to gravity. It is denoted by ‘g’.
→ Its unit is same as acceleration m/s .
Archimedes' principle
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Archimedes’ Principle
→ It states, when a body is immersed fully or partially in a fluid, it experiences a upward force
equal to the weight of the fluid displaced by it.
Applications of Archimedes’ Principle
i) It is used in determining relative density of substances.
(ii) It is used in designing ships and submarines.
(iii) Hydrometers and lactometers are made on this principle.
→ It is because of this ship made of iron and steel floats in water whereas a small piece of iron
in it.
buoyancy
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Buoyancy
→ The upward force experienced by an object when it is immersed into a fluid is called force of
buoyancy.
→ It acts in upward direction and it depends on the density of the fluid.
→ When force of gravitational attraction of the earth on the surface of the object < buoyant force
exerted by fluid on the surface of the object, object floats in the fluid.
• When force of gravitational attraction of the earth on the surface of the object > buoyant force
exerted by fluid on the surface of the object, the object sinks in the fluid.
→ This is the reason, why allpin sinks and boat/ship floats on the surface of water. (Archimedes
principle)
elementary idea of relative density
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Relative density
→ The ratio of the density of a substance to that of the density of water is called relative density.
• Relative density = Density of a substance/Density of water
→ It has no unit as it is a ratio.
Kepler’s laws of planetary motion
Kepler observed that different planets take different time to complete one revolution around the sun. From s this observation of planetary motion he deduced that square of time period is proportional to the cube ob its distance from the sun.
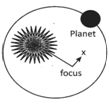
Kepler’s First Law
Kepler’s first law of planetary motion states that planets move around the sun in such a way that sun always remains at one of its focus.
Kepler’s second law
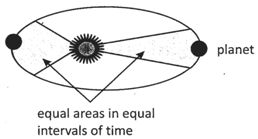
According to second law the line joining planet to the sun sweeps out equal area in equal time interval, as the planet revolve around the sun in a elliptical orbit.
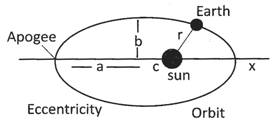
Kepler's Third Law
It states that square of time period is proportional to the cube of its semi major axis.
kinetic and potential energy
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Kinetic Energy
Objects in motion possess energy and can do work. This energy is called Kinetic Energy.
F = ma.
Also W = F.s
⇒ From the 2nd equation of motion v2−u2=2as,
⇒ we get s = v2−u2 / 2a
Substituting equation for work done by a moving body,
⇒ we get W =m.a * v2−u2 / 2a
Or
⇒ Kinetic Energy = K.E= 1/2 mv2 (taking initial velocity u=0)
When two identical bodies are in motion, the body with a higher velocity has more K.E.
Work-energy theorem
The work-energy theorem states that the net work done by a moving body can be calculated by finding the change in KE.
⇒ Wnet = KEfinal− KEinitial
⇒ Wnet = 1/2 mv2
Factors affecting kinetic energy
- Mass
- Velocity
- Momentum
Potential Energy
Energy can get stored in an object when work is done on it.
For example, stretching a rubber string. The energy that is possessed by a body by virtue of its configuration or change in position is known as Potential Energy.
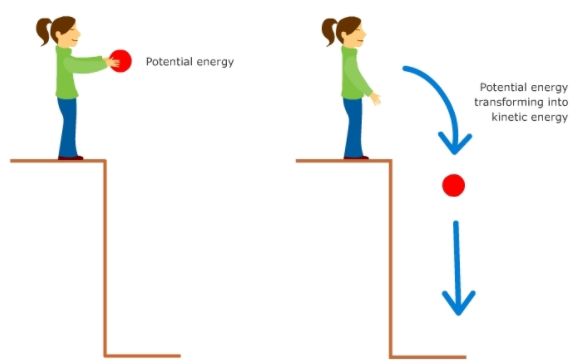
The potential energy of an object at a height.
When an object is raised to a certain height, work is done against gravity to change its position. This energy is stored as Potential Energy.
⇒W = F.s
⇒F = ma
In the case of increasing the height, F = mg
Therefore, W (P.E) = mgh
⇒ ΔPE = mg(hfinal - hinitial )
law of conservation of energy
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Law of Conservation of Energy
Law of conservation of energy states that energy can neither be created nor destroyed, but can be transferred from one form to another. The total energy before and after the transformation remains constant.
For example: consider a ball falling freely from a height.
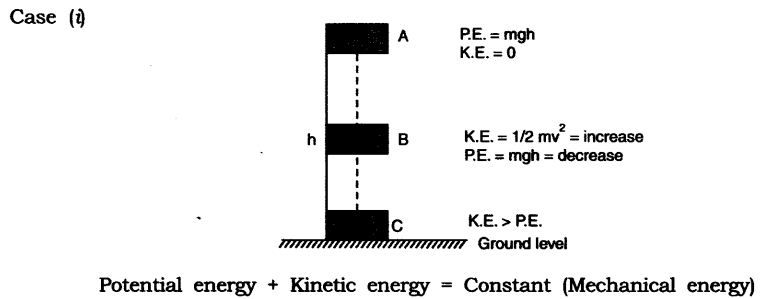
Potential energy + Kinetic energy = Constant (Mechanical energy)
A body of mass ‘m’ is raised to height ‘h’ at A its potential energy is maximum and kinetic energy is 0 as it is stationary.
When body falls at B, h is decreasing hence potential energy decreases and V is increasing hence kinetic energy is increasing.
When the body is about to reach the ground level, h = 0, v will be maximum hence kinetic energy –> potential energy
Decrease in potential energy = Increase in kinetic energy
This shows the continual transformation of gravitational potential energy into kinetic energy.
range of hearing in humans
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Range of Hearing
(i) Range of hearing in human is 20 Hz to 20000 Hz.
→ Children younger than 5 years and dogs can hear upto 25 Khz.
(ii) The sounds of frequencies lower than 20 Hz are
known as ‘infrasonic sounds’
→ A vibrating simple pendulum produces infrasonic sounds.
→ Rhinoceroses communicate each other using frequencies as low as 5 Hz.
→ Elephants and whales produces infrasonic waves.
→ Earthquakes produces infrasonic waves (before shock waves)
which some animals can hear and get disturbed.
(iii) The sounds of frequencies higher than 20 KHz are known as ‘ultrasonic waves’.
→ Dogs, parpoises, dolphins, bats and rats can hear ultrasonic sounds.
→ Bats and rats can produce ultrasonic sounds.
ultrasound
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Applications of Ultrasound
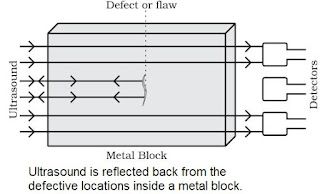
(i) It is used to detect cracks in metal blocks in industries without damaging them.
(ii) It is used in industries to clean ‘hard to reach’ parts of objects such as spiral tubes, odd shaped
machines etc.
(iii) It is used to investigate the internal organs of human body such as liver, gall bladder, kidney
uterus and heart.
(iv) Ecocardiography: These waves are used to reflect the action of heart and its images are
formed. This technique is called echocardiography.
(v) Ultrasonography: The technique of obtaining pictures of internal organs of the body by using
echoes of ultrasound waves is called ultrasonography.
(vi) Ultrasound is used to split tiny stones in kidneys into fine grains.
reflection of sound
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Reflection of Sound
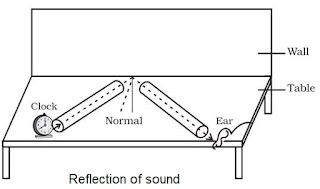
→ Like light, sound also bounce back when it falls on a hard surface. It is called reflection of sound.
• The laws of reflection of light are obeyed during reflection of sound.
(i) The incident sound wave, the reflected sound wave and normal at the point of incidence lie
same plane.
(ii) Angle of reflection of sound is always equal to the angle of incidence of sound.
Applications of Reflection of Sound
(i) Megaphone, loudspeakers, bulb horns and trumpets, shehnai etc. are designed to send sound to
a particular direction without spreading all around.
→ All these instruments have funnel tube which reflects sound waves repeatedly towards audio
In this amplitude of sound waves adds up to increase loudness of sound.

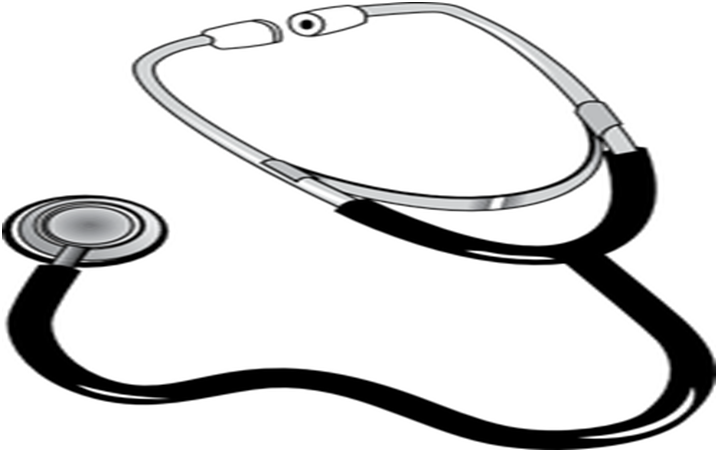
(ii) Stethoscope: It is a medical instrument used for listening the sounds produced in human bo
mainly in heart and lungs. The sound of the heartbeats reaches the doctor’s ears by the multipe
reflection of the sound waves in the rubber tube of stethoscope.
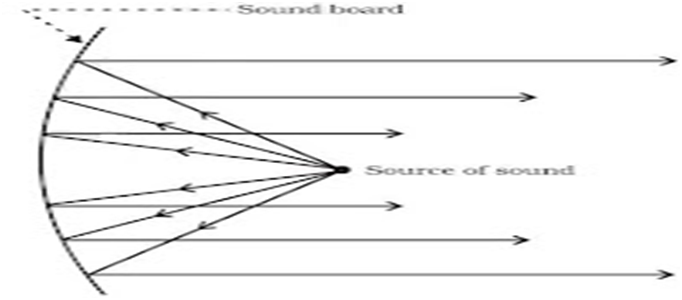
(iii) Sound Board: In big halls or auditoriums sound is absorbed by walls, ceiling, seats etc. So a
curved board (sound board) is placed behind the speakers so that his speech can be heard easily
by audiences. The soundboard works on the multiple reflection of sound.
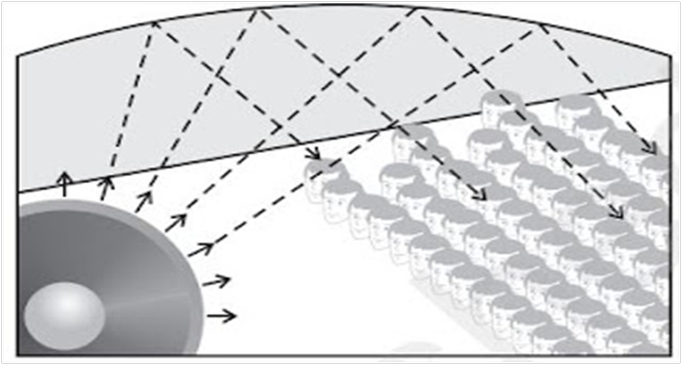
(iv) The ceiling of concert halls are made curved, so that sound after reflection from ceiling, rea
all the parts of the hall.
echo and SONAR
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Echo
• The repetition of sound caused by the reflection of sound waves is called an echo.
→ We can hear echo when there is a time gap of 0.1 second in original sound and echo (reflection of
sound).
→ Echo is produced when sound reflected from a hard surface (i.e. brick wall, mountain etc.) as
surface tends to absorb sound.
Minimum distance to hear an echo
Speed = Distance/Time
Here, Speed of sound in air = 344 ms -1 at 22ºC
Time = 0.1 second
344 = Distance/0.1 sec
⇒ Distance = 344 × 0.1 = 34.4 m
So, distance between reflecting surface and audience = 34.4/2 = 17.2 (at 22ºC).
Reverberation
• The persistence of sound in a big hall due to repeated reflection of sound from the walls, ceiling
and floor of the hall is called reverberation.
→ If reverberation is too long, sound becomes blurred, distorted and confusing due to overlapping
of different sound.
Methods to reduce reverberation in big halls or auditoriums
→ Panels made of felt or compressed fibre board are put on walls and ceiling to absorb sound
→ Heavy curtains are put on doors and windows.
→ Carpets are put on the floor.
→ Seats are made of material having sound absorbing properties.
SONAR
→ The word ‘SONAR’ stands for ‘Sound Navigation And Ranging’.
→ SONAR is a device which is used to find distance, direction and speed of underwater objects
→ SONAR consists of a transmitter and a receptor or detector and installed at the bottom of a sea
→ The transmitter produces and transmits ultrasonic waves.
→ These waves travel through water and after striking the objects on the bottom of sea, are
reflected back and received by detector.
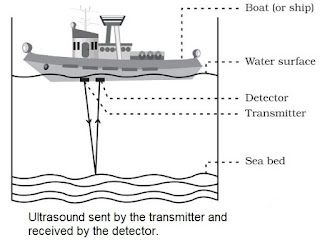
→ These reflected waves are converted into electric signals by detector.
→ The sonar device measures the time taken by ultrasound waves to travel from ship to bottom of
sea and back to ship.
→ Half of this time gives the time taken by the ultrasound waves from ship to bottom.
• Let the time interval between transmission and reception of ultrasound signal is t.
Speed of sound through sea water is v
Total distance travelled by waves = 2d.
→ The sonar is used to find the depth of sea, to locate underwater hills, valleys, submarines, ice
and sunken ships etc.
→ Bats fly in the dark night by emitting high pitched ultrasound waves which are reflected from
obstacle or prey and returned to bats ear.
→ The nature of reflection tells the bat where the obstacle or prey is and what it is like.
Structure of the human ear (auditory aspect only)
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Structure of The Human Ear
→ The ear consists of three parts: outer ear, middle ear and inner ear.
→ The ears are the sense organs which help us in hearing sound.
→ The outer ear is called pinna. It collects the sound from surroundings.
→ This sound passes through the auditory canal.
→ At the end of auditory canal, is a thin elastic membrane called ear drum or tympanic memb
→ The middle ear contains of three bones: hammer, anvil and stirrup linked with one another. F
end of hammer touches ear drum and that of stirrup linked with membrane of oval window of
ear.
→ The lower part of middle ear has a narrow ‘Eustachian tube’.
→ The inner ear has a coiled tube called cochlea, which is connected with oval window. Cochle
filled with a liquid containing nerve cells.
→ Other side of cochlea is connected to auditory nerve which goes to brain.
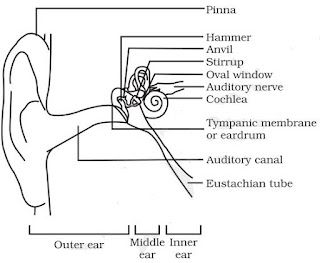
Working of Human ear
Pinna → Ear canal → Ear drum → Hammer → Anvil → Stirrup → Oval window → Cochlea → Audi
nerve → Brain
→ When compression of sound wave strikes the ear drum, the pressure on the outside of ear d
increases and pushes the ear drum inwards.
→ While during rarefaction ear drum moves outwards. Thus, ear drum starts vibrating back an
forth.
→ These vibrations are increased by three bones and middle ear transmits these amplified pre
variations received from sound waves to inner ear.
→ In the inner ear the pressure variations are turned into electric signals by the cochlea.
→ These electric signals are sent to the brain via auditory nerve and the brain interprets them
sound.
FRAME OF REFERENCE
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Rest & Motion Relative terms?
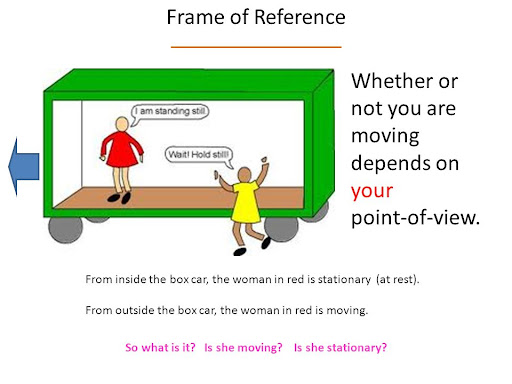
Frame of Reference - A frame of reference is another object or scene with respect to which we compare an object's position.
Objects changing positions with time with respect to the frame of reference are in motion while those which do not change position are at rest.
For example – A passenger sitting on a moving bus is at rest with respect to his co-passenger but at the same time, he is moving with the bus with respect to a person standing outside.
INTRODUCTION
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Introduction –
• In the physical world, one of the most common phenomena is motion.
• The branch of Physics, which deals with the behavior of moving objects, is known as mechanics.
• Mechanics is further divided into two sections namely Kinematics and Dynamics.
• Kinematics deals with the study of motion without taking into account the cause of motion.
• Dynamics is concerned with the cause of motion, namely force.
Motion and Rest -
• An object is said to be in motion if it changes its position with respect to its surroundings in a given time.
• An object is said to be at rest if it does not change its position with respect to its surroundings.
distance and displacement
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
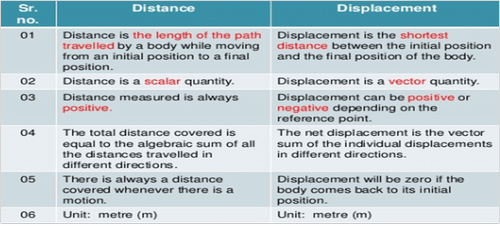
Distance and Displacement
Distance -The actual path or length travelled by the object travelled by the object is called the distance.
- It is a scalar quantity.
- It is always positive.
- It can never be zero or negative.
Displacement – It is the shortest path between initial and final point.
- It is a vector quantity.
- It can be positive or negative.
- It can be zero.
Difference b\w distance and displacement
• Example 1: A body travels in a semicircular path of radius 10 m starting its motion from point ‘A’ to point ‘B’. Calculate the distance and displacement.
• Example 2: A body travels 4 km towards North then he turn to his right and travels another 4 km before coming to rest. Calculate (i) total distance travelled, (ii) total displacement.
Speed
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Speed -
The measurement of distance travelled by a body per unit time is called speed.
Speed (v) = Distance Travelled/Time Taken = s/t
SI unit = m/s (meter/second)
Average Speed - The average speed of a body is the total distance travelled by the total time taken to cover this distance.
Average speed= Total Distance travelled / Total Time taken
EXAMPLE 1 - You walk 60 m at a speed of 3m/s and then run 140m at a speed of 7m/s along a straight track. Find the average speed?
EXAMPLE 2 - What will be the speed of body in m/s and km/hr if it travels 40 kms in 5 hrs ?
1. Introduction
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Introduction –
• In the physical world, one of the most common phenomena is motion.
• The branch of Physics, which deals with the behavior of moving objects, is known as mechanics.
• Mechanics is further divided into two sections namely Kinematics and Dynamics.
• Kinematics deals with the study of motion without taking into account the cause of motion.
• Dynamics is concerned with the cause of motion, namely force.
Motion and Rest
• An object is said to be in motion if it changes its position with respect to its surroundings in a given time.
• An object is said to be at rest if it does not change its position with respect to its surroundings.

Rest & Motion Relative terms?
1. Introduction
- Books Name
- Mayank classes Science Book
- Publication
- Mayank classes
- Course
- CBSE Class 9
- Subject
- Science
Introduction –
• In the physical world, one of the most common phenomena is motion.
• The branch of Physics, which deals with the behavior of moving objects, is known as mechanics.
• Mechanics is further divided into two sections namely Kinematics and Dynamics.
• Kinematics deals with the study of motion without taking into account the cause of motion.
• Dynamics is concerned with the cause of motion, namely force.
Motion and Rest
• An object is said to be in motion if it changes its position with respect to its surroundings in a given time.
• An object is said to be at rest if it does not change its position with respect to its surroundings.

Rest & Motion Relative terms?
1. Introduction
Chapter 8
Motion
Introduction
• One of the most common phenomena in the physical world is motion. Mechanics is the branch of Physics that deals with the behaviour of moving objects.
• Mechanics is divided further into two sections: Kinematics and Dynamics.
• Kinematics is the study of motion without regard for the cause of motion.
• Dynamics is concerned with the source of motion, which is force.
Motion and Rest:
• An object is said to be in motion if its position in relation to its surroundings changes in a given time.
• An object is said to be at rest if its position in relation to its surroundings does not change.
• A frame of reference is another object or scene against which we compare the position of an object.
Types of Motion:
There are three types of motion:
• Translatory motion
• Rotatory motion
• Vibratory motion
Translatory Motion:
• A particle in translatory motion moves from one point in space to another. This movement may be in a straight line or in a curved path.
• Rectilinear motion is defined as motion along a straight line.
• Curvilinear motion is defined as movement along a curved path.
• As an example, consider a car driving down a straight road.
Rotatory Motion:
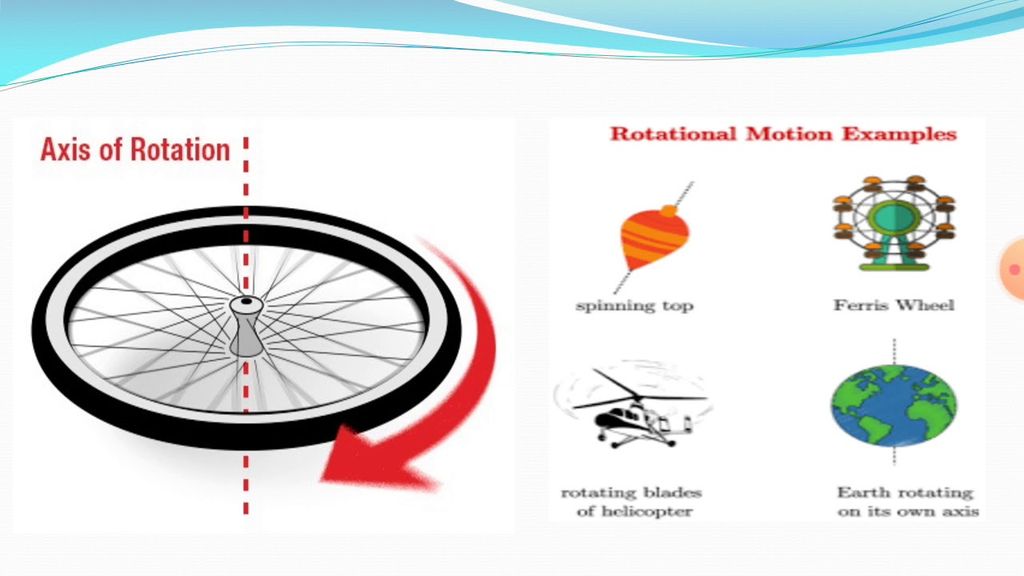
The particles of the body describe concentric circles around the axis of motion in rotatory motion.

Vibrational Motion:
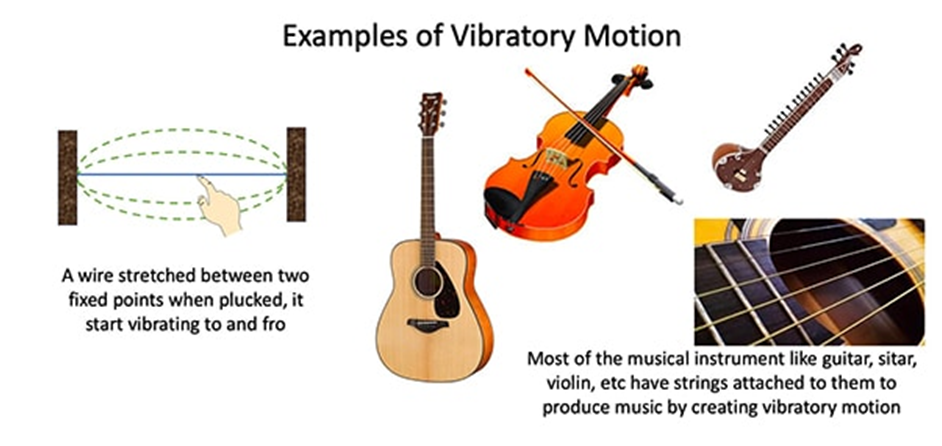
Particles in vibratory motion move back and forth around a fixed point.
1. Introduction
- Books Name
- Yash Tyagi Coaching Science Book
- Publication
- ACERISE INDIA
- Course
- CBSE Class 9
- Subject
- Science
Font Size
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substance[11]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substance[12]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substance[13]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substance[14]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substances[15]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substances[16]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substances[17]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substances[18]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substances[19]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substances[20]
2. Scalar and Vector Physical Quantities
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
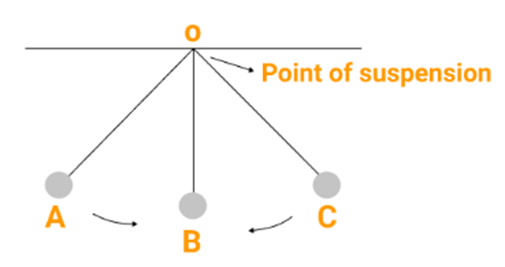
Frame of Reference - A frame of reference is another object or scene with respect to which we compare an object's position.
Objects changing positions with time with respect to the frame of reference are in motion while those which do not change position are at rest.
For example – A passenger sitting on a moving bus is at rest with respect to his co-passenger but at the same time, he is moving with the bus with respect to a person standing outside.
2. Scalar and Vector Physical Quantities
Scalar quantities
The quantities that depend upon magnitude and not the direction is called scalar quantities. They are represented as their own symbol.
Vector quantities
A physical quantity that depends upon magnitude as well as direction. They are represented by putting on their symbol.
Distance and Displacement:
Distance
• The distance travelled by a moving object is the length of the path the object takes.
• The measure of distance is a scalar quantity. The meter is the SI unit of distance.
Displacement
• It is the shortest path covered by a moving object in a specified direction from the point of reference (the initial position of the body).
• The meter is the SI unit of displacement.
• Displacement is a vector, which means that it is represented by a number with appropriate units and direction.
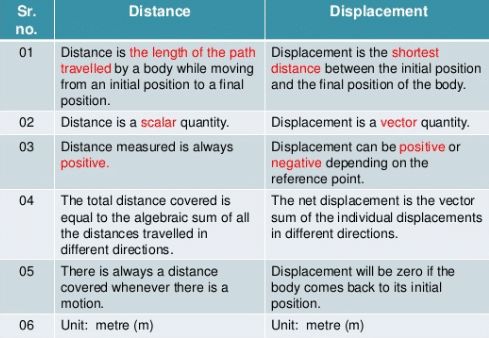
Difference between Distance and Displacement
|
Distance |
Displacement |
|
Distance provides the complete details of the path taken by the object |
Displacement does not provide the complete details of the path taken by the object |
|
Distance is always positive |
Displacement can be positive, negative or zero |
|
It is a scalar quantity |
It is a vector quantity |
|
The distance between two points may not be unique |
The displacement between two points is always unique |
3. Uniform and Non-Uniform Motion
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Types of Motion
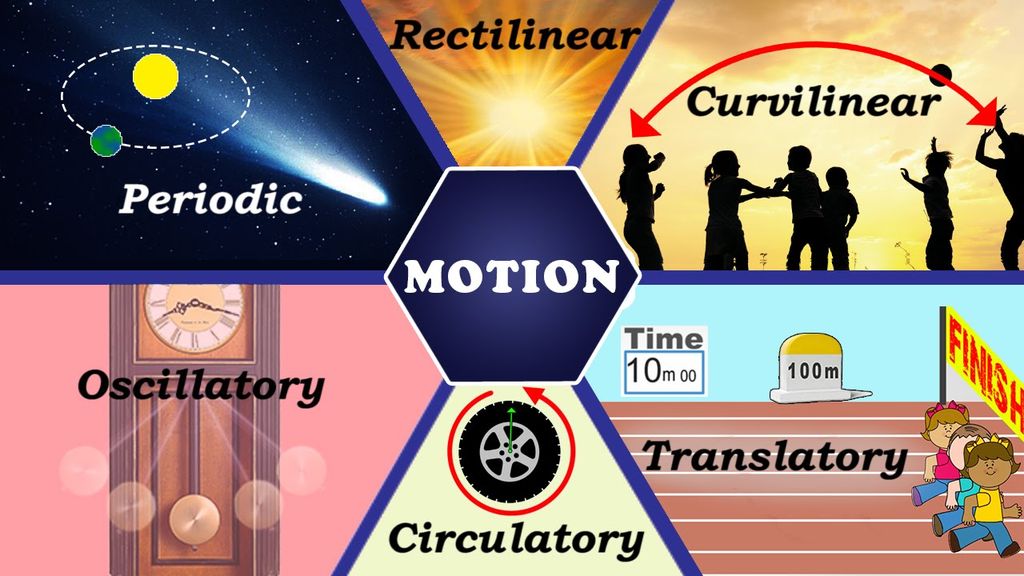
There are three types of motion:
• Translatory motion
• Rotatory motion
• Vibratory motion
Translatory Motion
• In translatory motion the particle moves from one point in space to another. This motion may be along a straight line or along a curved path.
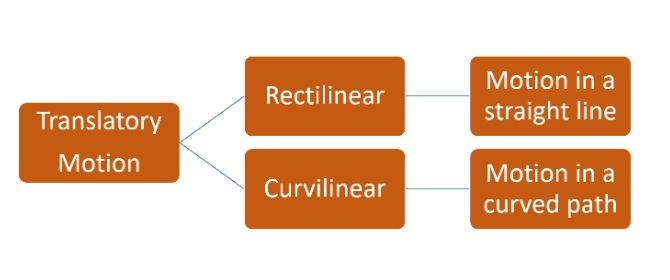
• Motion along a straight line is called rectilinear motion.
• Motion along a curved path is called curvilinear motion.
• Example: A car moving on a straight road
Curvilinear Motion
• Rotatory Motion - In rotatory motion, the particles of the body describe concentric circles about the axis of motion. Rotatory Motion
• Vibratory Motion - In vibratory motion the particles move to and fro about a fixed point.
3. Uniform and Non-Uniform Motion
Motion
Uniform Motion and Non-uniform Motion:
- If the body covers equal lengths in equal time intervals, so it is assumed to have a Uniform Motion.
- If the body covers unequal distances at equal intervals or equal distances at unequal intervals, so the body is said to have Non-uniform Motion.
Speed
Speed is defined as the total distance travelled by the object in the time interval during which the motion takes place. SI unit of speed is meter per second.
Speed = Distance Travelled / Time Taken
Velocity
The velocity of a body is known as the rate of change of displacement of a body with the passage of time. The velocity of a moving object is measured in meters per second in SI units.
Acceleration
Acceleration is a measure of the change in the velocity of an object per unit of time. SI unit of acceleration is ms-2. The equation can mathematically be written as:
Uniform Acceleration
The body is said to have a uniform acceleration if it is going on a straight path and the velocity shifts (increases or decreases) by equal proportions at equal time intervals.
Non-Uniform Acceleration
A body is said to have a non-uniform acceleration if the velocity shifts (increases or decreases) by unequal proportions at unequal time frames.
4. Derivation of Equation of Motion - Graphically,Circular Motion
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Physical Quantity – The term in which results of physics can be expressed and measured.
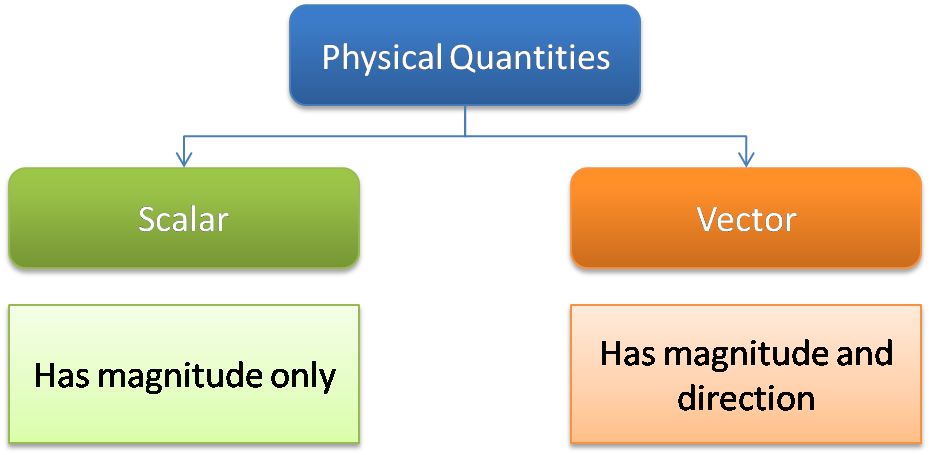
• Scalar quantity - It is the physical quantity having own magnitude but no direction.
For Example: distance, speed.
• Vector quantity - It is the physical quantity that requires both magnitude and direction.
For Example: displacement, velocity.

4. Derivation of Equation of Motion - Graphically,Circular Motion
Equation of motion by graphical methods
(i) Distance -Time Graph
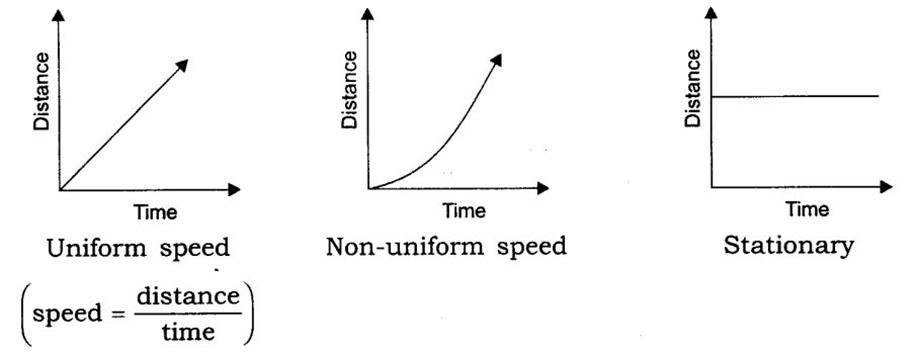
• Distance – Time Graphs represents a change in position of the object with respect to time. The graph in case the object is stationary (means the distance is constant at all time intervals) – Straight line graph parallel to x = axis
• For a distance-time graph, time is taken on x-axis and distance is taken on the y-axis.
• For a body at rest, as the slope is zero, so the speed of the body is zero
• For a body moving with uniform speed
• For an accelerated motion., the slope of the graph is increasing with time
• For decelerated (speeding down) motion, the slope of the graph is decreasing with time.
(ii) Velocity- Time Graph
• Constant velocity is a straight-line graph, velocity is always parallel to the x-axis. When a body is moving with a uniform velocity, the slope of AB indicates zero acceleration.
• When a body starts from rest and moves with uniform acceleration, then it is greater is the slope of the v-t graph, greater will be the acceleration.
• When a body is moving with uniform acceleration and its initial velocity is not zero.
• When a body is moving with increasing acceleration, the slope gradually increases with time.
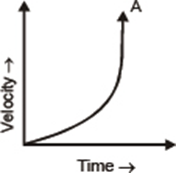
• When a body is moving with decreasing acceleration, the slope decreases with time.
• When a body is moving with uniform retardation and its initial velocity is not zero, as θ > 90°, the graph has a negative slope.
Derivations
(i)velocity-time relation:

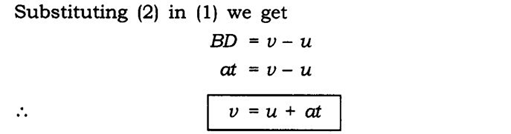
(ii) Position-time relation:
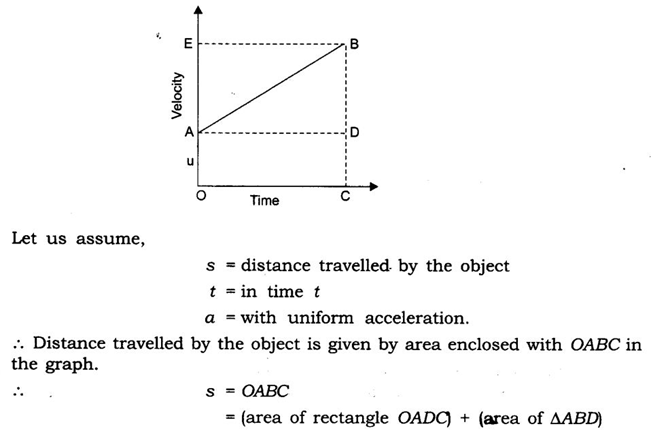
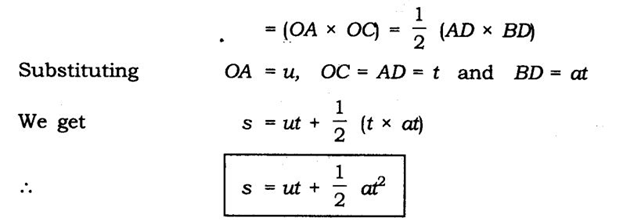
(iii) Position-velocity relation:
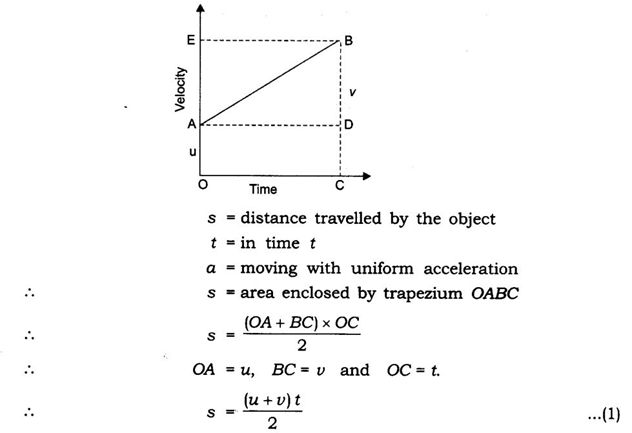
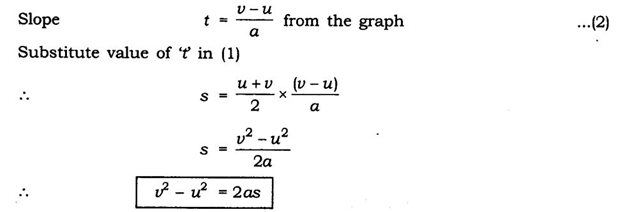
Uniform circular motion
When a body moves in a circular path with uniform speed, its motion is called uniform circular motion.
5. Equation Of Motion By Graphical Method
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Distance and Displacement
Distance -The actual path or length travelled by the object travelled by the object is called the distance.
- It is a scalar quantity.
- It is always positive.
- It can never be zero or negative.
Displacement – It is the shortest path between initial and final point.
- It is a vector quantity.
- It can be positive or negative.
- It can be zero.
Difference b\w distance and displacement
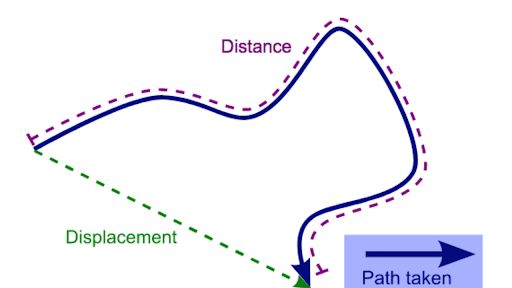
-
Example 1: A body travels in a semicircular path of radius 10 m starting its motion from point ‘A’ to point ‘B’. Calculate the distance and displacement.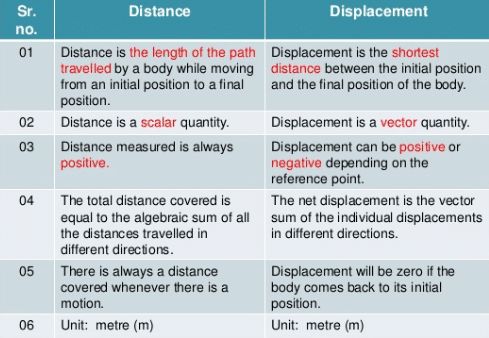
- Example 2: A body travels 4 km towards North then he turn to his right and travels another 4 km before coming to rest. Calculate (i) total distance travelled, (ii) total displacement.
UNIFORM MOTION AND NON-UNIFORM MOTION
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Uniform Motion and Non-uniform Motion
- Uniform motion - When a body covers equal distances in equal intervals of time then the body is said to describe uniform motion.
- Non uniform motion - When a body moves unequal distances in equal intervals of time or vice-versa, then the body is said to describe non-uniform motion.

NON UNIFORM MOTION
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Non uniform motion - When a body moves unequal distances in equal intervals of time or vice-versa, then the body is said to describe non-uniform motion.
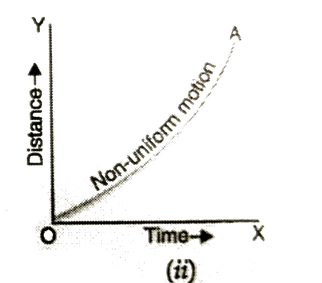
SPEED AND AVERAGE SPEED
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Speed - The measurement of distance travelled by a body per unit time is called speed.
• Speed (v) = Distance Travelled/Time Taken = s/t
• SI unit = m/s (meter/second)
Average Speed - The average speed of a body is the total distance travelled by the total time taken to cover this distance.
- Average speed= Total Distance travelled / Total Time taken
- EXAMPLE 1 - You walk 60 m at a speed of 3m/s and then run 140m at a speed of 7m/s along a straight track. Find the average speed?
- EXAMPLE 2 - What will be the speed of body in m/s and km/hr if it travels 40 kms in 5 hrs ?
AVERAGE SPEED
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Average Speed - The average speed of a body is the total distance travelled by the total time taken to cover this distance.
- Average speed= Total Distance travelled / Total Time taken
- EXAMPLE 1 - You walk 60 m at a speed of 3m/s and then run 140m at a speed of 7m/s along a straight track. Find the average speed?
- EXAMPLE 2 - What will be the speed of body in m/s and km/hr if it travels 40 kms in 5 hrs ?
VELOCITY AND AVERAGE VELOCITY
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Velocity - It is defined as the displacement of the body per unit time.
Velocity = displacement travelled / time taken
SI unit = m/s (meter/second)
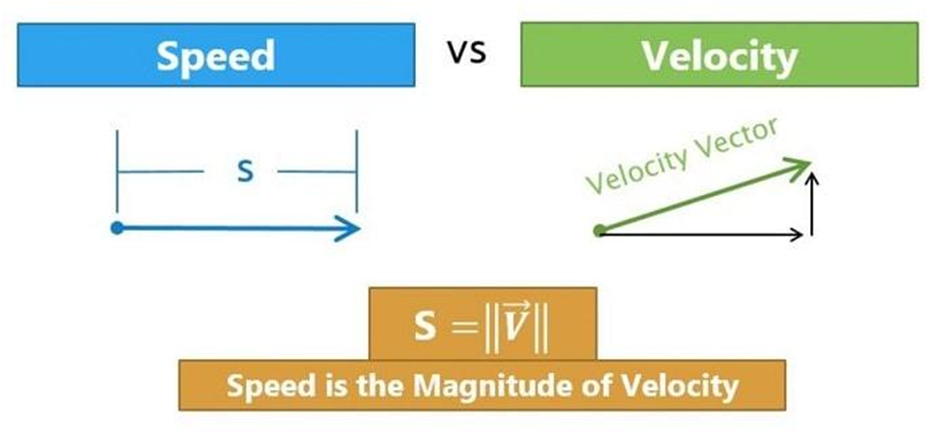
Average Velocity - The average velocity of a body is the total displacement travelled by the total time taken to cover this distance.
Average velocity= Total Displacement/Total Time taken
Avg. Velocity (vavg) = (Initial velocity + Final velocity)/2 = (u+v)/2
where, u = initial velocity, v = final velocity
Example 1: During first half of a journey by a body it travel with a speed of 40 km/hr and in the next half it travels with a speed of 20 km/hr. Calculate the average speed of the whole journey.
Example 2 : If Ananya was able to travel 6 km in North in 2 hour in his car. What was her velocity?
Example 3: A car travels 20 km in first hour, 40 km in second hour and 30 km in third hour. Calculat the average speed of the train.
AVERAGE VELOCITY
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Average Velocity - The average velocity of a body is the total displacement travelled by the total time taken to cover this distance.
Average velocity= Total Displacement/Total Time taken
Avg. Velocity (vavg) = (Initial velocity + Final velocity)/2 = (u+v)/2
where, u = initial velocity, v = final velocity
Example 1: During first half of a journey by a body it travel with a speed of 40 km/hr and in the next half it travels with a speed of 20 km/hr. Calculate the average speed of the whole journey.
Example 2 : If Ananya was able to travel 6 km in North in 2 hour in his car. What was her velocity?
Example 3: A car travels 20 km in first hour, 40 km in second hour and 30 km in third hour. Calculat the average speed of the train.
ACCELERATION/ RETARDATION
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Acceleration - Acceleration is seen in non-uniform motion and it can be defined as the rate of change of velocity with time.
- Acceleration (a) = Change in velocity/Time = (v-u)/t
where, v = final velocity, u = initial velocity
- If v > u, then ‘a’ will be positive (+ve).
Retardation/Deceleration - Deceleration is seen in non-uniform motion during decrease in velocity with time. It has same definition as acceleration
- Deceleration (a') = Change in velocity/Time = (v-u)/t
- Here, v < u, ‘a’ = negative (-ve).
- It is a vector quantity.
- SI unit – m/s2 ( meter per second square)
Example 1: A car speed increases from 40 km/hr to 60 km/hr in 5 sec. Calculate the acceleration of car.
Example 2: A car travelling with a speed of 20 km/hr comes into rest in 0.5 hrs. What will be the valu of its retardation?
EXAMPLE 3 : If the velocity of the car reduced to 80 m/s from 120 m/s in 8 seconds on applying breaks . Calculate its acceleration.
6. Uniform Circular Motion
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Uniform Acceleration - If the change in velocity in equal intervals of time is always the same, then the object is said to be moving with uniform acceleration.
Example: a body falling from a height towards the surface of the earth.
Non-uniform or Variable Acceleration- If the change in velocity in equal intervals of time is not the same, then the object is said to be moving with variable acceleration.
Example - A ball thrown vertically upwards is moving with a negative acceleration as the velocity decreases with time.
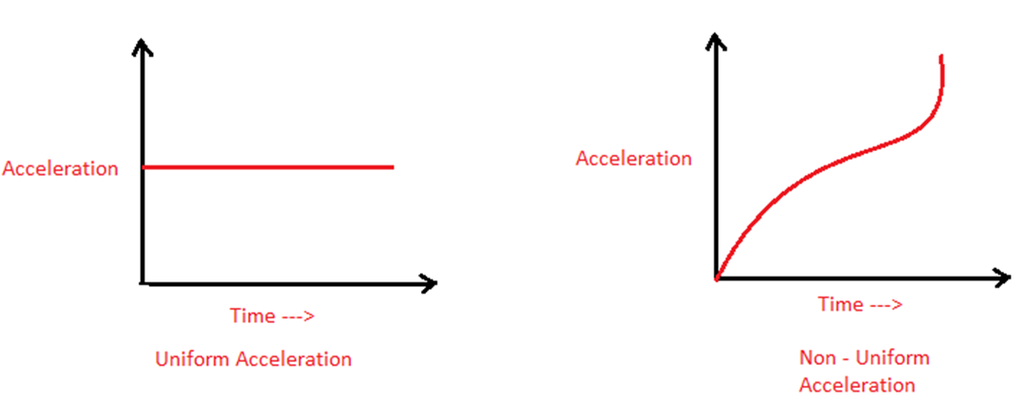
GRAPHS OF MOTION
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Graphs for Motion -
1) Distance-time graphs (s-t graphs)
a) When the object is stationary or at rest -
The distance time graph for stationary object is the line parallel to time axis.
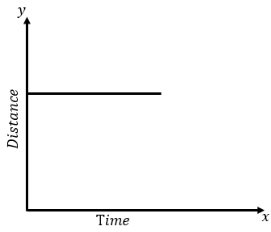
b) When object is in uniform motion -
The distance time graph for the object moving in uniform motion is the straight line inclined to time axis.
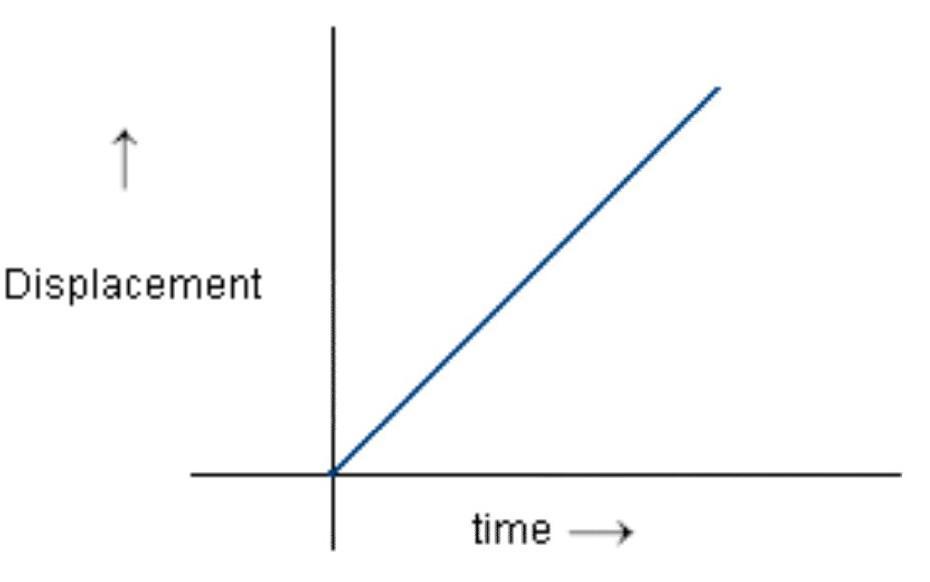
C) When object is in non-uniform motion -
The distance time graph for object moving in non -uniform motion is the curved line.
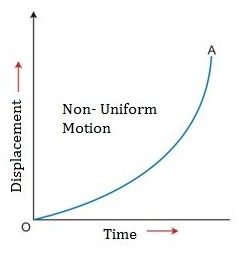
Important results of distance time graphs -
1) area under curve of s-t graph = displacement/distance travelled by the object
2) slope of s-t graph = velocity of the object
Velocity time graphs (v-t graphs)
a) When object is moving with constant speed -
The velocity time graph for an object moving with constant/same speed is given by a straight line parallel to time axis.
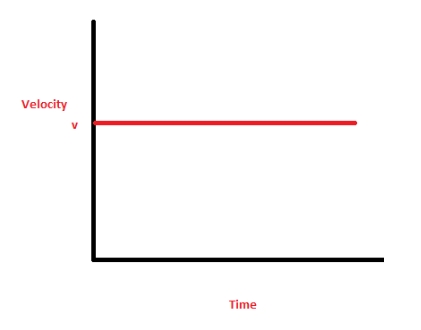
b) When object is in uniform motion -
The velocity tiem graph for an object in uniform motion is the straight line inclined to time axis.
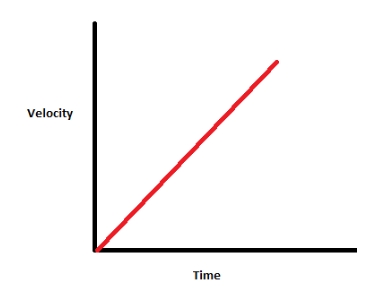
C) When object is in non-uniform motion -
The distance time graph for object moving in non -uniform motion is the curved line.
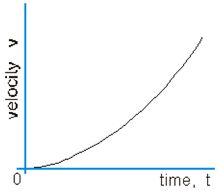
Important results of velocity time graphs -
1) area under curve of v-t graph = displacement/distance travelled by the object
2) slope of v-t graph = acceleration of the object
EQUATIONS OF MOTION AND DERIVATION OF EQUATIONS BY GRAPHICAL METHOD
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Definition of Equations of Motion
Equations of motion, in physics, are defined as equations that describe the behaviour of a physical system in terms of its motion as a function of time.
There are three equations of motion that can be used to derive components such as displacement(s), velocity (initial and final), time(t) and acceleration(a). The following are the three equation of motion:
- First Equation of Motion : v=u+at
- Second Equation of Motion : s=ut+1/2 at2
- Third Equation of Motion : v2=u2+2as
DERIVATION OF FIRST EQUATION OF MOTION ( V = u+at )
Consider a body of mass “m” having initial velocity “u”. Let after time “t” its final velocity becomes “v” due to uniform acceleration “a”.
Now as we know that,
Acceleration = change in velocity/Time taken Acceleration = Final velocity-Initial velocity / time taken
a = v-u/t
=> at = v-u
or v = u + at
This is the first equation of motion.
DERIVATION OF SECOND EQUATION OF MOTION (S=ut+1/2 at2 )
Consider a body of mass “m” having initial velocity “u”. Let after time “t” its final velocity becomes “v” due to uniform acceleration “a”. Let the distance travelled by the body be “s”.
Now As we know that,
Distance = Average velocity X Time
Also, Average velocity = u+v/2
Distance (s) = ( u+v ) *t/2 …….eq.(1)
Again we know that, v = u + at
By substituting this value of “v” in eq.(1), we get
Distance(s) = (u+u+at) *t/2
=> s = (2u+at)* t/2
=> s = 2ut/2+at2/2
=>s = ut+ at2/2
or s = ut + 1/2 at2
This is the second equation of motion.
DERIVATION OF THIRD EQUATION OF MOTION (V2 = u2+2as)
Consider a body of mass “m” having initial velocity “u”. Let after time “t” its final velocity becomes “v” due to uniform acceleration “a”. Let the distance travelled by body be “s”.
Displacement=(Initial Velocity+Final Velocity)×t/2
Substituting the standard notations, the above equation becomes
s=(u+v)×t/2
From the first equation of motion, we know that
v=u+at
Rearranging the above formula, we get
t=v−u/a
Substituting the value of ‘t’ in the displacement formula, we get
s=(v+u)/2 *(v−u)/a
s=(v2 - u2)/2a
2as= v2 - u2
Rearranging, we get
v2 – u2= 2as This is the third equation of motion.
UNIFORM CIRCULAR MOTION
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
What is Uniform Circular Motion?
The movement of a body following a circular path is called a circular motion. Now, the motion of a body moving with constant speed along a circular path is called Uniform Circular Motion. Here, the speed is constant but the velocity changes.
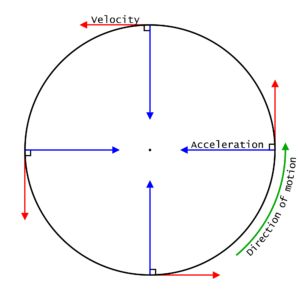
NOTE -
So if a particle is moving in a uniform circular motion:
1) Its speed is constant
2) Velocity is changing at every instant
Uniform Circular Motion Examples
Following are the examples of uniform circular motion:
- Motion of artificial satellites around the earth is an example of uniform circular motion. The gravitational force from the earth makes the satellites stay in the circular orbit around the earth.
- The motion of electrons around its nucleus.
- The motion of blades of the windmills.
- The tip of second’s hand of a watch with circular dial shows uniform circular motion.
Formula for veocity in UCM -
V=2πR/T
where R is radius of circle, T is time taken
introduction
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Introduction
→ Force: It is the force that enables us to do any work. To do anything, either we pull or push the object. Therefore, pull or push is called force.
Example, to open a door, either we push or pull it. A drawer is pulled to open and pushed to close.
1. Introduction
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Introduction
→ Force: It is the force that enables us to do any work. To do anything, either we pull or push the object. Therefore, pull or push is called force.
Example, to open a door, either we push or pull it. A drawer is pulled to open and pushed to close.
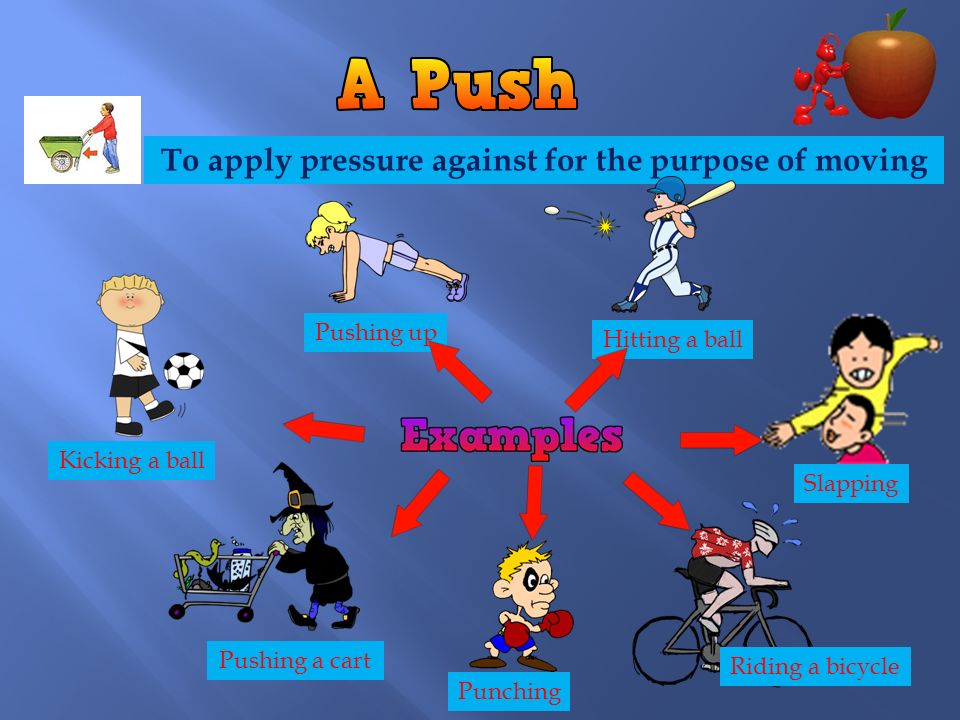

Effects of Force
→ Force can make a stationary body in object.
For example: a football can be set to move by kicking it i.e. by applying a force.

→ Force can stop a moving body.
For example, by applying brakes, a running cycle or a running vehicle can be stopped.

→ Force can change the direction of a moving object.
For example: by applying force i.e. by moving handle, the direction of a running bicycle can be changed. Similarly by moving steering, the direction of a running vehicle is changed.

→ Force can change the speed of a moving body. By accelerating, the speed of a running vehicle can be increased or by applying brakes the speed of a running vehicle can be decreased.

→ Force can change the shape and size of an object.
For example: by hammering, a block of metal can be turned into a thin sheet. By hammering, a stone can be broken into pieces.

1. Introduction
Force and Laws of Motion
Introduction
What is Force?
It is a push or pulls on an object that produces an acceleration in the body on which it acts. S.I. unit of force is Newton.
A force can do three things on a body.
• It can change the speed of the body.
• It can change the direction of motion of a body.
• It can change the shape of a body.
Balanced Forces – When equal amounts of forces are applied to an object from different directions such that they cancel out each other, such forces are known as balanced forces.
• Balanced forces do not change the state of rest or motion of an object.
• Balanced forces may change the shape and size of an object.
• If forces nullify one another then their resultant force is zero.
Unbalanced Force – When forces applied to an object are of different magnitude (or not in opposite directions to cancel out each other), such forces are unbalanced forces.
• Unbalanced forces can alter the state of rest or motion of an object.
• Unbalanced forces can cause acceleration in an object.
• Unbalanced forces can change the shape and size of an object.
2. Newton's Law of Motion
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
• Forces are mainly of two types:
(i) Balanced forces
(ii) Unbalanced forces

Balanced Forces
→ If the resultant of applied forces is equal to zero, it is called balanced forces.
Example: In the tug of war if both the team apply similar magnitude of forces in opposite directions, rope does not move in either side.
This happens because of balanced forces in which resultant of applied forces become zero.
→ Balanced forces do not cause any change of state of an object. Balanced forces are equal in magnitude and opposite in direction.
→ Balanced forces can change the shape and size of an object.
For example: When forces are applied from both sides over a balloon, the size and shape of balloon is changed.
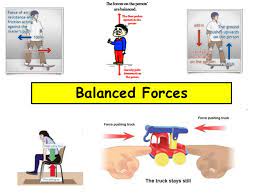
Unbalanced Forces
→ If the resultant of applied forces are greater than zero, the forces are called unbalanced forces.
→ An object in rest can be moved because of applying balanced forces.
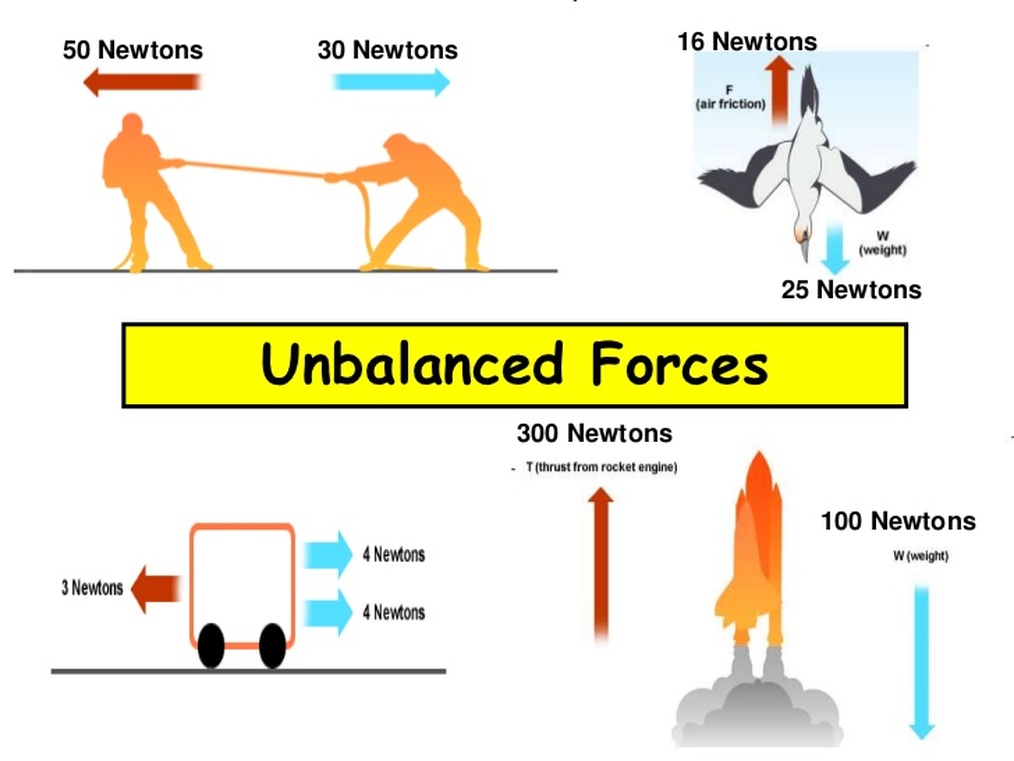
• Effects of Unbalanced forces -
→ Move a stationary object
→ Increase the speed of a moving object
→ Decrease the speed of a moving object
→ Stop a moving object
→ Change the shape and size of an object
2. Newton's Law of Motion
Force of Friction
It is a force extended when two surfaces are in contact with each other. It always acts in a direction opposite to the direction of motion of the object.
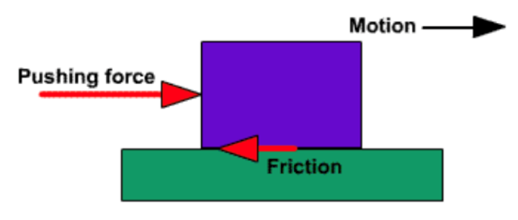
First law of motion: An object remains in a state of rest or of uniform motion in a straight line unless acted upon by an external unbalanced force.
Inertia: The natural tendency of an object to resist a change in their state of rest or of uniform motion is called inertia.
1. The mass of an object is a measure of its inertia.
2. Its S.I. unit is kg.
3. A body with greater mass has greater inertia.
Example of Inertia
• We fall back when a vehicle starts moving in the forward direction because our body is in the rest state and it opposes the motion of the vehicle.
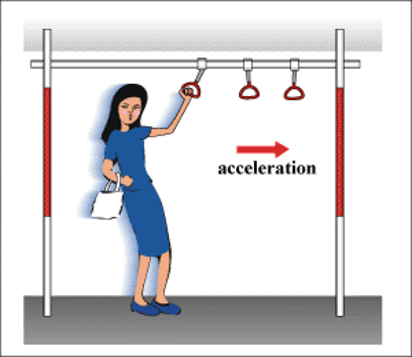
The second law of motion: The rate of change of momentum of an object is proportional to the applied unbalanced force in the direction of the force.
Momentum: The momentum of an object is the product of its mass and velocity and has the same direction as that of the velocity.
1.Its S.I. unit is kg m/s.
2.It is a vector quantity.
1 Newton: A force of one Newton produces an acceleration of 1 m/s2 on an object of mass 1 kg.
IN. = 1 kg m/s2 (F = ma)
For Example –
A cricketer when catches a ball pulls his hands in the backward direction to give some time to decrease the velocity of the ball. As the acceleration of the ball decreases the force exerted on catching the moving ball also decreases. If the cricketer would try to stop a moving ball suddenly, he would have to apply a larger force.
Third law of motion: To every action, there is an equal and opposite reaction and they act on two different bodies.
For Example, a ball when it hits the ground (action) bounces back with a certain force reaction.
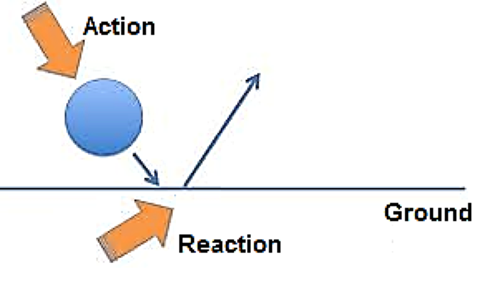
EFFECT OF UNBALANCED FORCE
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Unbalanced Forces
→ If the resultant of applied forces are greater than zero, the forces are called unbalanced forces.
→ An object in rest can be moved because of applying balanced forces.

• Effects of Unbalanced forces -
→ Move a stationary object
→ Increase the speed of a moving object
→ Decrease the speed of a moving object
→ Stop a moving object
→ Change the shape and size of an object
3. Law of Conversation of Momentum
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Laws of Motion
• Galileo Galilei: Galileo first of all said that object move with a constant speed when no forces act on them.
→ This means if an object is moving on a frictionless path and no other force is acting upon it, the object would be moving forever. That is, there is no unbalanced force working on the object. But practically it is not possible for any object.
→ Force of friction, force of air and many other forces are always acting upon an object.
Newton’s Laws of Motion
→ Newton studied the ideas of Galileo and gave the three laws of motion. These laws are known as Newton’s laws of motion.
Newton’s First Law of Motion (Law of Inertia)
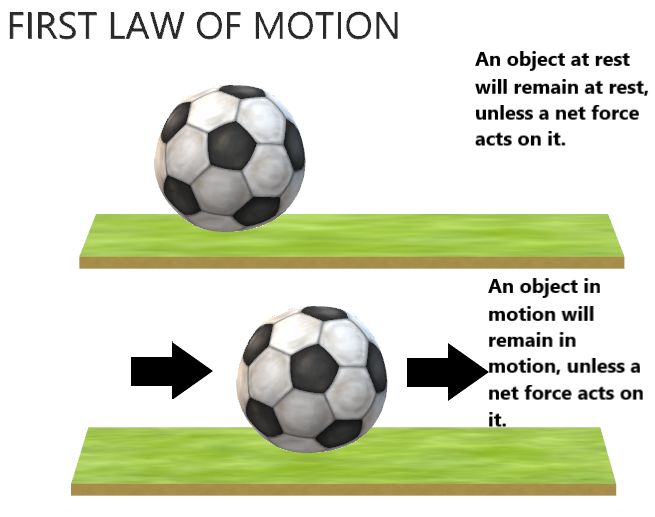
→ Any object remains in the state of rest or in uniform motion along a straight line, until it is compelled to change the state by applying external force.
Explanation: If any object is in the state of rest, then it will remain in rest until a external force is applied to change its state. Similarly, an object will remain in motion until any external force is applied over it to change its state.
This means all objects resist to in changing their state. The state of any object can be changed by applying external forces only, this property is called inertia.
• Newton’s First Law of Motion in Everyday Life
(i) A person standing in a bus falls backward when bus starts moving suddenly.
→ This happens because the person and bus both are in rest while bus is not moving, but as the bus starts moving, the legs of the person start moving along with bus but rest portion of his body has the tendency to remain in rest. Because of this, the person falls backward; if he is not alert.
(ii) A person standing in a moving bus falls forward if driver applies brakes suddenly.
→ This happens because when bus is moving, the person standing in it is also in motion along with bus. But when driver applies brakes the speed of bus decreases suddenly or bus comes in the state of rest suddenly, in this condition the legs of the person which are in contact with the bus come in rest while the rest part of his body have the tendency to remain in motion. Because of this person falls forward if he is not alert.
(iii) Before hanging the wet clothes over laundry line, usually many jerks are given to the clothes to get them dried quickly. Because of jerks, droplets of water from the pores of the cloth falls on the ground and reduced amount of water in clothes dries them quickly.
→ This happens because when suddenly clothes are made in motion by giving jerks, the water droplets in it have the tendency to remain in rest and they are separated from clothes and fall on the ground.
(iv) When the pile of coin on the carom-board is hit by a striker, coin only at the bottom moves away leaving rest of the pile of coin at same place.
→ This happens because when the pile is struck with a striker, the coin at the bottom comes in motion while rest of the coin in the pile has the tendency to remain in the rest and they vertically falls the carom-board and remain at same place.
3. Law of Conversation of Momentum
Conservation of momentum
If the external force on a system is zero, the momentum of the system remains constant i.e., in an isolated system, the total momentum remains conserved.
Suppose A and B are two balls, they have mass m1 and m2 and initial velocities u1 and u2 as shown in above figure before collision. The two bodies collide and force is exerted by each body. There is change in their velocities due to collision.
NEWTONS LAW OF MOTION
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Newton’s Laws of Motion
→ Newton studied the ideas of Galileo and gave the three laws of motion. These laws are known as Newton’s laws of motion.
Newton’s First Law of Motion (Law of Inertia)

→ Any object remains in the state of rest or in uniform motion along a straight line, until it is compelled to change the state by applying external force.
Explanation: If any object is in the state of rest, then it will remain in rest until a external force is applied to change its state. Similarly, an object will remain in motion until any external force is applied over it to change its state.
This means all objects resist to in changing their state. The state of any object can be changed by applying external forces only, this property is called inertia.
• Newton’s First Law of Motion in Everyday Life
(i) A person standing in a bus falls backward when bus starts moving suddenly.
→ This happens because the person and bus both are in rest while bus is not moving, but as the bus starts moving, the legs of the person start moving along with bus but rest portion of his body has the tendency to remain in rest. Because of this, the person falls backward; if he is not alert.
(ii) A person standing in a moving bus falls forward if driver applies brakes suddenly.
→ This happens because when bus is moving, the person standing in it is also in motion along with bus. But when driver applies brakes the speed of bus decreases suddenly or bus comes in the state of rest suddenly, in this condition the legs of the person which are in contact with the bus come in rest while the rest part of his body have the tendency to remain in motion. Because of this person falls forward if he is not alert.
(iii) Before hanging the wet clothes over laundry line, usually many jerks are given to the clothes to get them dried quickly. Because of jerks, droplets of water from the pores of the cloth falls on the ground and reduced amount of water in clothes dries them quickly.
→ This happens because when suddenly clothes are made in motion by giving jerks, the water droplets in it have the tendency to remain in rest and they are separated from clothes and fall on the ground.
(iv) When the pile of coin on the carom-board is hit by a striker, coin only at the bottom moves away leaving rest of the pile of coin at same place.
→ This happens because when the pile is struck with a striker, the coin at the bottom comes in motion while rest of the coin in the pile has the tendency to remain in the rest and they vertically falls the carom-board and remain at same place.
4. Second Law Of Motion
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Mass and Inertia
→ The property of an object because of which it resists to get disturb its state is called inertia.
→ Inertia of an object is measured by its mass. Inertia is directly proportional to the mass. This means inertia increases with increase in mass and decreases with decrease in mass.
→ A heavy object will have more inertia than the lighter one. In other words, the natural tendency of an object that resists the change in state of motion or rest of the object is called inertia.

→ Since a heavy object has more inertia, thus it is difficult to push or pull a heavy box over the ground than the lighter one.
5. Third Law Of Motion
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Momentum
→ Momentum is the power of motion of an object.
→ The product of velocity and mass is called the momentum. Momentum is denoted by ‘p’.
→ Therefore, Momentum of the object = Mass × Velocity (p = m × v)
where, p = momentum, m = mass of the object and v = velocity of the object.
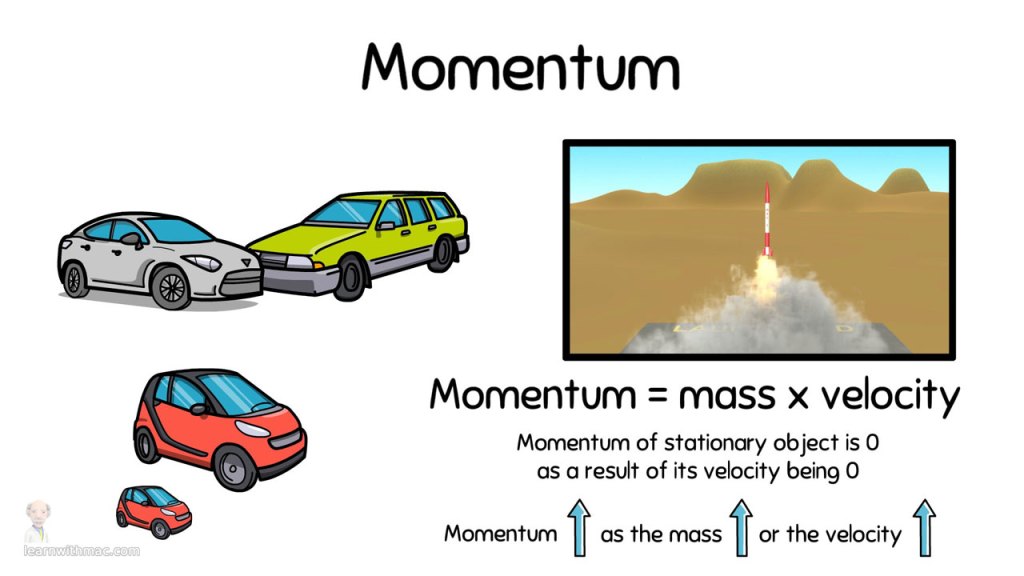
• Some explanations to understand the momentum:
→ A person get injured in the case of hitting by a moving object, such as stone, pebbles or anything because of momentum of the object.
→ Even a small bullet is able to kill a person when it is fired from a gun because of its momentum due to great velocity.
→ A person get injured severely when hit by a moving vehicle because of momentum of vehicle due to mass and velocity.
Momentum and Mass
→ Since momentum is the product of mass and velocity (p = m × v) of an object. This means momentum is directly proportional to mass and velocity. Momentum increases with increase of either mass or velocity of an object.
→ This means if a lighter and a heavier object is moving with same velocity, then heavier object will have more momentum than the lighter one.
→ If a small object is moving with great velocity, it has tremendous momentum. And because of momentum, it can harm an object more severely.
Example: a small bullet having a little mass even kills a person when it is fired from a gun.
→ Usually, road accidents prove more fatal because of high speed than in slower speed. This happens because vehicles running with high speed have greater momentum compared to a vehicle running with slower speed.
Momentum of an object which is in the state of rest
Let an object with mass ‘m’ is in the rest.
Since, object is in rest, therefore, its velocity, v = 0
Now we know that,
Momentum = mass × velocity
⇒ p = m × 0 = 0
Thus, the momentum of an object in the rest i.e. non-moving, is equal to zero.
Unit of momentum
→ SI unit of mass = kg
→ SI unit of velocity = m/s
We know that,
Momentum (p) = m × v
∴ p = kg × m/s ⇒ p = kg m/s
Numerical Problems Based on Momentum
Type I: Calculation of Momentum
Example 1: What will be the momentum of a stone having mass of 10 kg when it is thrown with a velocity of 2 m/s?
Solution
Mass (m) = 10 kg
Velocity (v) = 2 m/s
We know that,
Momentum (p) = Mass (m) × Velocity (v)
∴ p = 10 kg × 2 m/s = 20 kg m/s
Thus, the momentum of the stone = 20 kg m/s.
Example 2: Calculate the momentum of a bullet of 25 g when it is fired from a gun with a velocity of 100 m/s.
Solution
Given, Velocity of the bullet (v) = 100 m/s
Mass of the bullet (m) = 25 g = 25/1000 kg = 0.025 kg
Since, p = m × v
∴ p = 0.025 × 100 = 2.5 kg m/s
Momentum of the bullet = 2.5 kg m/s.
Example 3: Calculate the momentum of a bullet having mass of 25 g is thrown using hand with a velocity of 0.1 m/s.
Solution
Given, Velocity of the bullet (v) = 0.1 m/s
Mass of the bullet (m) = 25 g = 25/1000 kg = 0.025 kg
Momentum (p) = Mass (m) × Velocity (v)
∴ p = 0.025 kg × 0.1 m/s
⇒ p = 0.0025 kg m/s
Momentum of the bullet = 0.0025 kg m/s.
Example 4: The mass of a goods lorry is 4000 kg and the mass of goods loaded on it is 20000 kg. If the lorry is moving with a velocity of 2 m/s, what will be its momentum?
Solution
Given, Velocity (v) = 2 m/s
Mass of lorry = 4000 kg
Mass of goods on the lorry = 20000 kg
∴ Total mass (m) on the lorry = 4000 kg + 20000 kg = 24000 kg
Momentum (p) = Mass (m) × Velocity (v)
∴ p = 24000 kg × 2 m/s
⇒ p = 48000 kg m/s
Momentum of the lorry = 48000 kg m/s.
Example 5: A car having mass of 1000 kg is moving with a velocity of 0.5 m/s. What will be its momentum?
Solution
Given, Velocity of the car (v) = 0.5 m/s
Mass of the car (m) = 1000 kg
Momentum (p) = Mass (m) × Velocity (v)
∴ p = 1000 kg × 0.5 m/s = 500 kg m/s
Momentum of the car = 500 kg m/s.
6. Conservation Of Momentum
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Statement of Second Law of Motion
→ Rate of change of momentum of an object is proportional to applied unbalanced force in the direction of force.
Mathematical expression
Suppose, Mass of an object = m kg
Initial velocity of an object = u m/s
Final velocity of an object = v m/s
∴ Initial momentum, p1 = mu
Final momentum, p2 = mv
∴ Change in momentum = Final momentum – Initial momentum
= mv – mu
= m(v – u)
∴ Rate of change of momentum = Change in momentum/Time taken
= m(v-u)/t
• According to 2nd law, this rate of change is momentum is directly proportional to force.
We know that, a = (v-u)/t (From 1st equation of motion)
∴ F = kma
where, k is a constant. Its value can be assumed as 1.
∴ F = 1 × m × a = ma
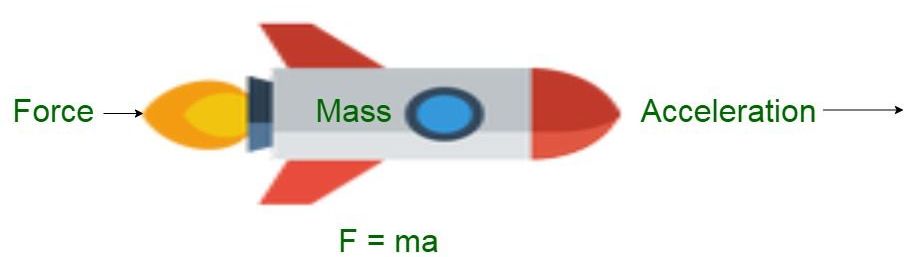
• SI unit = kg m/s2 or Newton
1 Newton: When an acceleration of 1 m/s2 is seen in a body of mass 1 kg, then the
force applied on the body is said to be 1 Newton.
Proof of Newton’s First Law of Motion from Second Law
→ First law states that if external force F = 0, then a moving body keeps moving with the same velocity, or a body at rest continues to be at rest.
∴ F = 0
We know, F = m(v-u)/t
(i) A body is moving with initial velocity u then,
m(v-u)/t = 0 ⇒ v – u = 0
∴ v = u
Thus, final velocity is also same.
(ii) A body is at rest i.e., u = 0
Therefore, from above u = v = 0
So, the body will continue to be at rest.
THIRD LAW OF MOTION
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Third Law of Motion
→ For every action there is an equal an opposite reaction.

Applications
(i) Walking is enabled by 3rd law.
(ii) A boat moves back when we deboard it.
(iii) A gun recoils.
(iv) Rowing of a boat.
LAW OF CONSERVATION OF MOMENTUM
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Law of Conservation of Momentum
→ When two (or more) bodies act upon one another, their total momentum remains constant (or conserved) provided no external forces are acting.
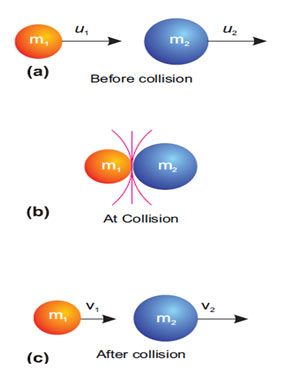
• Initial momentum = Final momentum
Suppose, two objects A and B each of mass m1 and mass m2 are moving initially with velocities u1 and u2, strike each other after time t and start moving with velocities v1 and v2 respectively.
Now, Initial momentum of object A = m1u1
Initial momentum of object B = m2u2
Final momentum of object A = m1v1
Final momentum of object B = m2v2
so, Rate of change of momentum in A,
F1 = (m1v1 - m1u1)t = m1(v1 - u1)/t ....(i)
Rate of change of momentum in B,
F2 = (m2v2 – m2u2)t = m2(v2 - u2)/t ....(ii)
We know from 3rd law of motion,
F1 = −F2
So, m1(v1 - u1)/t = - m2(v2 - u2)/t
⇒ m1v1 – m1u1 = -m2v2 + m2u2
⇒ m1u1 + m2u2 = m1v1 + m2v2
Thus, Initial momentum = Final momentum
Example 1: A bullet of mass 20 g is fired horizontally with a velocity of 150 m/s from a pistol of mass 2 kg. Find the recoil velocity of the pistol.
Solution
Given, Mass (m1) of bullet = 20 g = 0.02 kg
Mass (m2) of pistol = 2 kg
Initially bullet is inside the gun and it is not moving.
∵ Mass = m1+m2 = (0.02 + 2) kg = 2.02 kg
and u1 = 0
∴ Initial momentum = 2.02 × 0 = 0 ....(i)
Let the velocity of pistol be v2 and v1 for bullet = 150
∴ Final momentum = m1v1 + m2v2 = 0.02×150 + 2v2 ...(ii)
We know that,
Initial momentum = Final momentum
∴ (0.02×150)/100 + 2v2 = 0 [From equations (i) and (ii)]
⇒ 3 + 2v2 = 0
⇒ 2v2 = −3
⇒ v2 = −1.5 m/s
(−)ve sign indicates that gun recoils in direction opposite to that of the bullet.
Example 2: Two hockey players viz A of mass 50 kg is moving with a velocity of 4 m/s and another one B belonging to opposite team with mass 60 kg is moving with 3 m/s, get entangled while chasing and fall down. Find the velocity with which they fall down and in which direction?
Solution
Given,
mA = 50 kg, uA = 4 m/s
mB = 60 kg, uB = 3 m/s
Initial momentum A = mAuA = 50 × 4 = 200 kgm/s
Initial momentum B = MBuB = 60 × 3 = 180 kgm/s
∴ Total initial momentum = 200 + 180 = 380 kgm/s ....(i)
Final momentum = (mA + mB)v = (50 + 60)v = 110v ....(ii)
According to the law of conservation of momentum,
380 = 110v
⇒ v = 380/110 = 3.454 m/s
Questions -
1. State two effects of force.
2. Scientist who first conducted experiment to form the base for Newton's first law of motion.
3. If first law of motion holds true, why does a ball rolling on ground stop on its own?
4. What would happen if there was no friction on the Earth?
5. Why is it dangerous to jump out of a moving bus?
6. Define force and its various types. What is its unit?
7. What is the negative effect of friction on your shoe soles?
8. You are applying force on the pan of single pan weighing balance and the pointer points to 100 g. What is the force in newtons applied by you?
9. An athlete always runs some distance before taking a jump. Why?
10. A cricket ball of mass 70 g moving with a velocity of 0.5 m/s is stopped by a player in 0.5 s. What is the force applied by the player to stop the ball?
11. In a cricket match, why does a player lower his hands slightly while catching the ball?
12. Two cars having masses in the ratio 4 : 5, accelerate in the ratio 2:3. Find the ratio of forces exerted by each of them.
1. Introduction
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Introduction
→ Gravitational Force of Earth: If we release a small stone without pushing it from a height, it
accelerates towards earth. Earth attracts everything towards it by an unseen force of attraction. This force of attraction is known as gravitation or gravitational pull

Universal Law of Gravitation
→ Sir Isaac Newton in 1687 proposed a law about the force of attraction between the
objects in the universe which is known as Newton’s law of gravitation.
According to Universal law of Gravitation
→ Every mass in this universe attracts every other mass with a force which is directly proportional to
the product of two masses and inversely proportional to the square of the distance between them
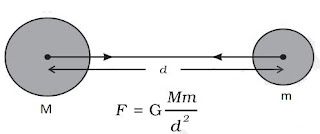
• Let masses (M) and (m) of two objects are distance (d) apart, then force of attraction (F) between
them
F ∝ M×m
F ∝ 1/d2
F ∝ Mm/d2
F = (GMm)/d2
where,
G is a constant and is known as Gravitational constant.
Value of G = 6.67×10-11 Nm2/kg2
G is called universal gravitational constant.
→ If unit of F is in Newton, m is in kg, d is in mere, then unit of G can be calculated as :
G = (F×d2)/Mm, therefor unit will be Nm2/kg2
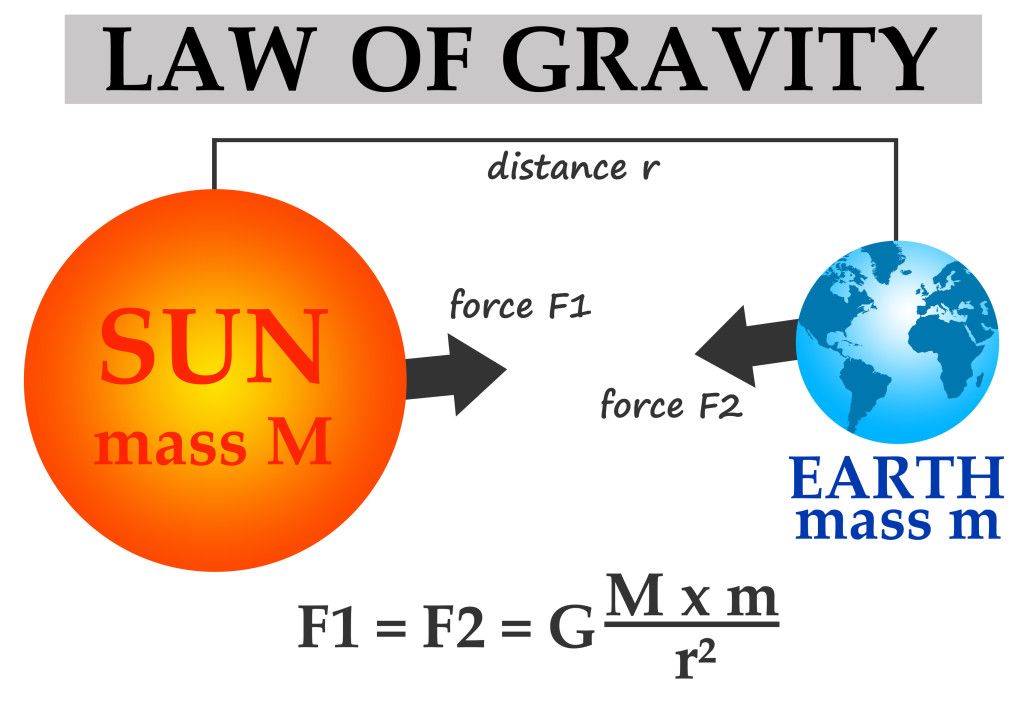
Importance of universal law of gravitation
(i) The force that binds us to the earth.
(ii) The motion of moon around the earth.
(iii) The motion of earth around the sun.
(iv) The tides due to moon and the sun.
1. Introduction
Chapter 10
Gravitation
Introduction
Gravitational force of Earth:
- If we release a small stone without pushing it from a height it accelerates towards Earth. The stone is when accelerated towards earth, means some force is acting on it.
- The force which pulls the object towards the centre of earth is known as gravitational force of the earth. Here, stone also attracts the earth.
- It means every object in universe attracts every other object.
- When a body undergoes circular motion, it experiences a force that acts towards the centre of the circle. This centre-seeking force is called a centripetal force.
Universal Law of Gravitation
- According to the universal law of gravitation, every object attracts every other object with a force.
- This force is directly proportional to the product of their masses.
- This force is inversely proportional to the square of distances between them.
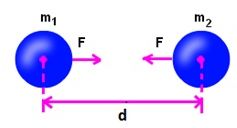
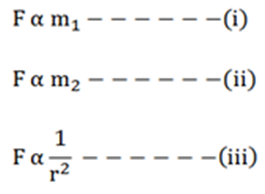
From the above equation we can rewrite them as the following:
![]()
If we remove the proportionality, we get proportionality constant G as the following:
![]()
According to, Newton’s universal Law of gravitation
G = Fr2/ m1 m2
SI Unit: Nm2 kg-2
Value of G = 6.673 × 10-11 Nm2 kg-2
The proportionality constant G is also known as the Universal Gravitational Constant.
Importance of universal law of gravitation
It explains:
- the force that binds us to the earth.
- the motion of moon around the earth
- the motion of planets around the sun.
- the tides due to the moon and the sun.
2. Gravitational Constant and its Units
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Free fall of an object and acceleration (g)
→ When an object is thrown upward, it reaches certain height, then it starts falling down towar
earth. It is because the earth’s gravitational force exerts on it.
→ This fall under the influence of earth is called ‘free fall of an object’.

→ During this free fall direction do not change but velocity continuously changes which is calle
acceleration due to gravity. It is denoted by ‘g’.
→ Its unit is same as acceleration m/s .
2. Gravitational Constant and its Units
Freefall
• When an object falls down towards the earth under the gravitational force alone, we say the object is in free fall.
• The velocity of a freely falling body changes and is said to be accelerated.
• This acceleration is called acceleration due to gravity, denoted by ’g’. Unit is m/s2.
• The motion of objects under the influence of gravity ‘g’ does not depend on the mass of the body. All objects fall at the same rate.
We know that, F= ma
Therefore, F = mg
The force (F) of gravitational attraction on a body of mass m due to earth of mass M and radius R is given by
![]()
g. But the acceleration due to gravity is represented by the symbol g. Therefore, we can write
h. F = mg ... (2)
i. From the equation (1) and (2), we get
![]()
j. When body is at a distance ‘r’ from the centre of the earth then
![]()

Weight of object on the moon
Just like the Earth, the Moon also exerts a force upon objects. Hence, objects on moon also have some weight. The weight will not be same as than on the earth. So, weight on the Moon can be calculated as -

3. Weight and Mass
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Gravitational Acceleration and its value at the surface of earth
→ The uniform acceleration produced in a freely falling object due to the gravitational force of
earth, is called acceleration due to gravity.
→ It is represented by ‘g’ and it always acts towards the centre of the earth.
Mathematical Expression for g
From the second law of motion, force is the product of mass and acceleration.
F = ma
For free fall, acceleration is replaced by acceleration due to gravity.
Therefore, force becomes:
F = mg ….(i)
But from Universal Law of Gravitation,
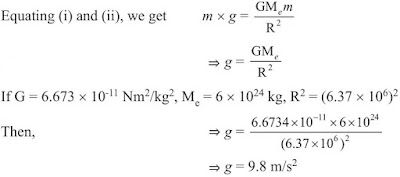
Factors Affecting the Value of g
- As the radius of the earth increases from the poles to the equator, the value of g becomes greater at the poles than at the equator.
- As we go at large heights, value of g decreases.
To Calculate the Value of g
Value of universal gravitational constant, G = 6.7 × 10–11 N m2/ kg2,
Mass of the earth, M = 6 × 1024 kg, and
Radius of the earth, R = 6.4 × 106 m
Putting all these values in equation (iii), we get:
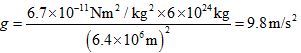
Thus, the value of acceleration due to gravity of the earth, g = 9.8 m/s2.
3. Weight and Mass
Mass:
• Mass of an object is the measure of its inertia.
• It is the matter present in it. It remains the same everywhere in the universe.
Weight:
• The force of attraction of the earth on the object is known as the weight of the object.
• It’s S.I. unit is Newton.
W = m x g
Thrust:
• The force that acts in the perpendicular direction is called thrust.
• It is similar to force applied to an object
• It is a vector quantity.
Pressure
• The force that acts per unit area of the object is pressure.
• It is the thrust per unit area.
• Pressure is denoted by ‘P'
• P = thrust/ area = force/ area = F/A
• SI unit: N/m2 or Pa (Pascal)
Applications of pressure
• The base of high buildings is made wider so that weight of the walls act over a large surface area and pressure is less.
• School bags are having broad strap so that the weight of the school bags fall over a large area of shoulder and produce less pressure and become less painful.
• All liquids and gases exist pressure in all direction.
4. Buoyancy and Density
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Difference between Gravitation Constant (G) and Gravitational Acceleration (g)

Motion of Objects Under the Influence of Gravitational Force of the Earth
Let an object is falling towards earth with initial velocity u. Let its velocity, under the effect of gravitational acceleration g, changes to v after covering the height h in time t.
Then the three equations of motion can be represented as:
Velocity (v) after t seconds, v = u + ght
Height covered in t seconds, h = ut + ½gt2
Relation between v and u excluding t, v2 = u2 + 2gh
The value of g is taken as positive in case of the object is moving towards earth and taken as negative in case of the object is thrown in opposite direction of the earth.
4. Buoyancy and Density
Buoyancy
• Whenever an object is immersed in a liquid, the liquid exerts a buoyant force or upthrust in the opposite direction of the gravitational force. This is also called the Force of Buoyancy.
• It depends upon the density of the fluid.
• Therefore, an object is able to float in water when the gravitational force is less than the buoyant force.
• Similarly, an object sinks into the water when the gravitational force is larger than the buoyant force.
Archimedes principle
• According to the Archimedes principle, whenever an object is immersed in a liquid (fully or partially), the liquid exerts an upward force upon the object. The amount of that force is equivalent to the weight of the liquid displaced by the object.
Why does an object sink or float on water?
• An object can sink or float on water based on its density with respect to water. The density is defined as mass per unit volume.
• Objects having a density less than water float in it. For Example, Cork flows in water because its density is lower than that of water.
• Objects that have a density higher than water sink in it. For Example, Iron nail sinks in water because the density of iron is more than water's density.
Thus, we can conclude that buoyancy depends upon:
The density of the liquid
The volume of the object (as the volume of object increases, its density decreases and vice-versa
Application of Archimedes Principle:
• In evaluating relative density
• In designing ships and submarines
• In making lactometers and hydrometers
Relative Density
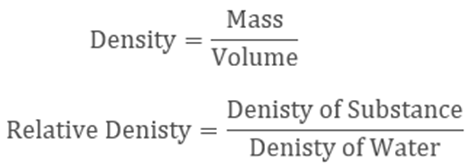
MOTION OF OBJECT UNDER GRAVITY
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Motion of Objects Under the Influence of Gravitational Force of the Earth
Let an object is falling towards earth with initial velocity u. Let its velocity, under the effect of gravitational acceleration g, changes to v after covering the height h in time t.
Then the three equations of motion can be represented as:
Velocity (v) after t seconds, v = u + ght
Height covered in t seconds, h = ut + ½gt2
Relation between v and u excluding t, v2 = u2 + 2gh
The value of g is taken as positive in case of the object is moving towards earth and taken as negative in case of the object is thrown in opposite direction of the earth.
5. Archimedes'S Principle
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Mass & weight
Mass (m)
- The mass of a body is the quantity of matter contained in it.
- Mass is a scalar quantity which has only magnitude but no direction.
- Mass of a body always remains constant and does not change from place to place.
- SI unit of mass is kilogram (kg).
- Mass of a body can never be zero.
Weight (W)
- The force with which an object is attracted towards the centre of the earth, is called the weight of the object.
Now, Force =m×a
But in case of earth,a=g
∴F=m×g
But the force of attraction of earth on an object is called its weight (W).
∴W=mg - As weight always acts vertically downwards, therefore, weight has both magnitude and direction and thus it is a vector quantity.
- The weight of a body changes from place to place, depending on mass of object.
- The SI unit of weight is Newton.
- Weight of the object becomes zero if g is zero.
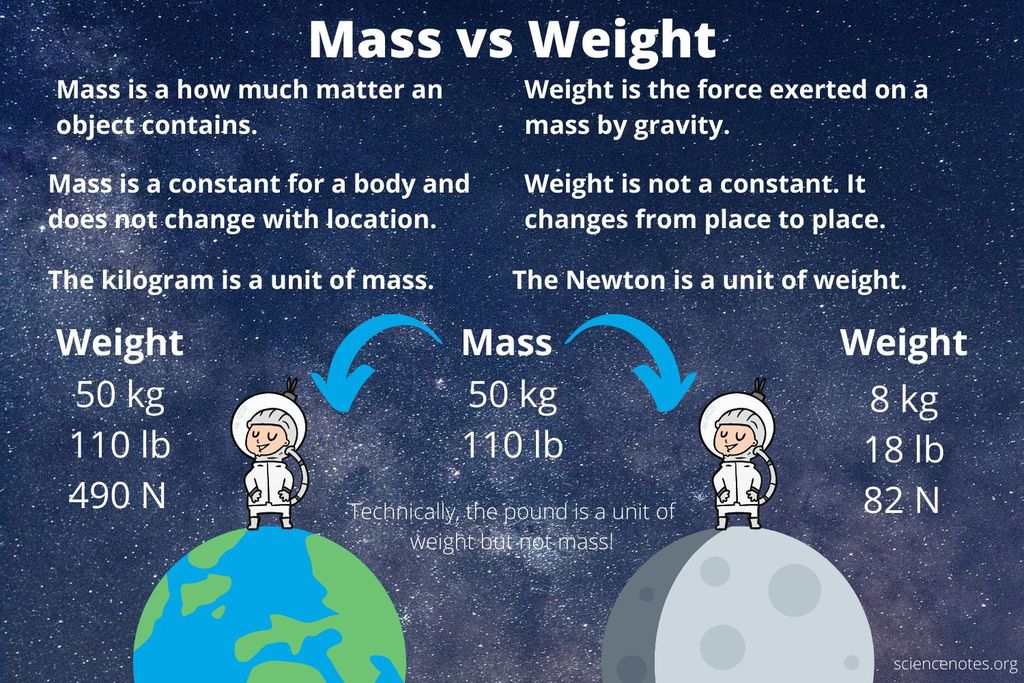
Weight of an Object on the Surface of Moon
Mass of an object is same on earth as well as on moon. But weight is different.
weight of the object on the moon = (1/6) × its weight on the earth.
INTRODUCTION, THRUST & PRESSURE
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Introduction
Floatation depends upon the density. If an object has density less than the density of water, it floats. Principle of floatation is stated by the Archimedes. This chapter deals with what is floatation, laws of floatation, its applications and examples.
Thrust and Pressure
Force acting on an object perpendicular to the surface is called thrust.
Effect of thrust depends on the area of contact.
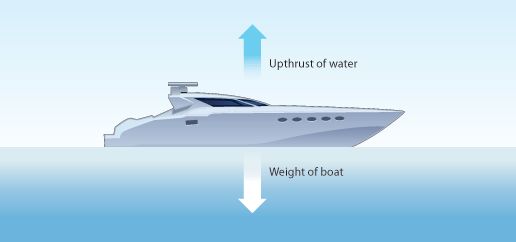
The pressure is thrust per unit area.
SI unit is the pascal (Pa).
Force acting on a smaller area applies more pressure than the same force acting on a larger area.
FACTORS AFFECTING PRESSURE
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
• Pressure depends on two factors
(i) Force applied
(ii) Area of surface over which force acts
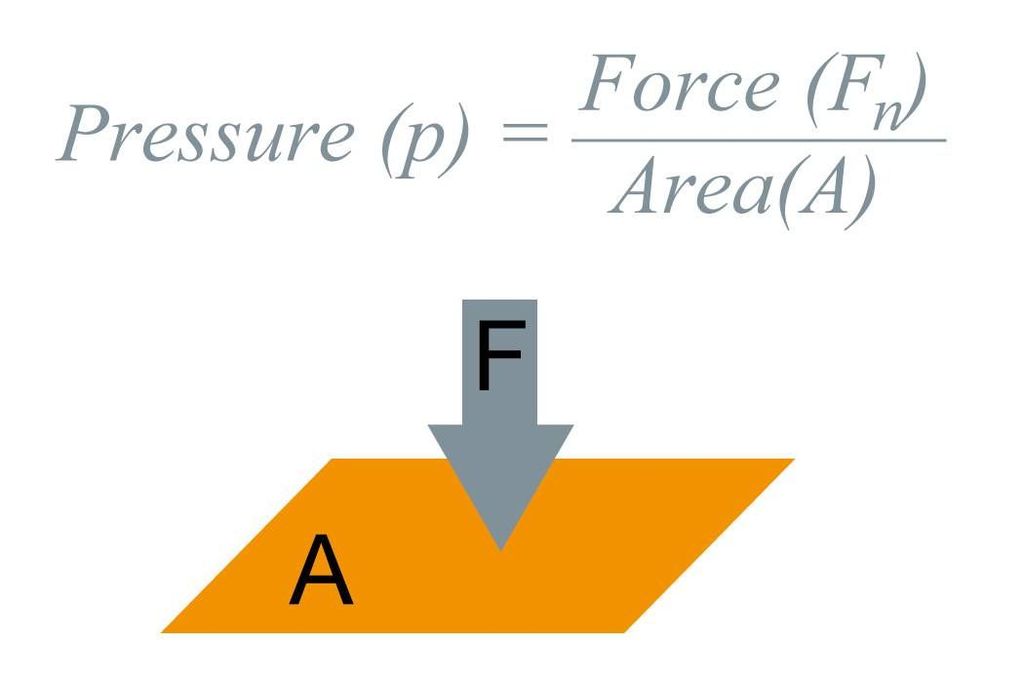
Examples of Pressure
→ The base of high buildings is made wider so that weight of walls act over a large surface are
pressure is less.
→ School bags are having broad strap so that the weight of school bags fall over a larger area so that student feel less pressure on shoulders.
--> liquids and gases are fluids and they exert pressure in all directions.

BUOYANCY
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Buoyancy
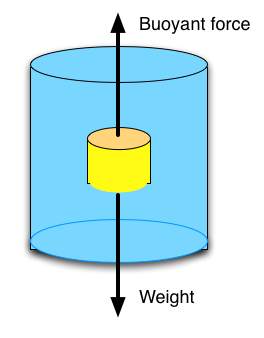
→ The upward force experienced by an object when it is immersed into a fluid is called force of
buoyancy.
→ It acts in upward direction and it depends on the density of the fluid.
→ When force of gravitational attraction of the earth on the surface of the object < buoyant force
exerted by fluid on the surface of the object, object floats in the fluid.
• When force of gravitational attraction of the earth on the surface of the object > buoyant force
exerted by fluid on the surface of the object, the object sinks in the fluid.
→ This is the reason, why allpin sinks and boat/ship floats on the surface of water. (Archimedes
principle)
DENSITY AND RELATIVE DENSITY
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Density

→ The mass per unit volume is called density of an object.
→ If M is the mass and V is the volume, then
• Density (d) = Mass(M)/Volume(V)
• SI unit = kg/m3
ARCHIMEDES PRINCIPLE
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Archimedes’ Principle
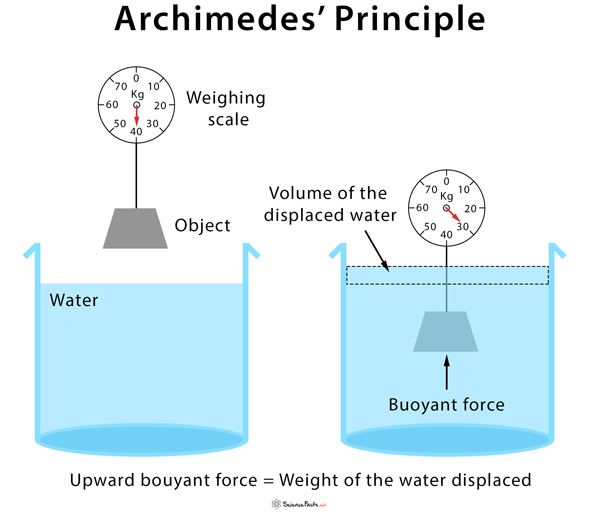
→ It states, when a body is immersed fully or partially in a fluid, it experiences a upward force
equal to the weight of the fluid displaced by it.
Applications of Archimedes’ Principle
i) It is used in determining relative density of substances.
(ii) It is used in designing ships and submarines.
(iii) Hydrometers and lactometers are made on this principle.

→ It is because of this ship made of iron and steel floats in water whereas a small piece of iron
in it.
Relative density
→ The ratio of the density of a substance to that of the density of water is called relative density.
• Relative density = Density of a substance/Density of water
→ It has no unit as it is a ratio.
KEPLER'S LAWS
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Kepler’s laws of planetary motion
Kepler observed that different planets take different time to complete one revolution around the sun. From s this observation of planetary motion he deduced that square of time period is proportional to the cube ob its distance from the sun.
Kepler’s First Law
Kepler’s first law of planetary motion states that planets move around the sun in such a way that sun always remains at one of its focus.
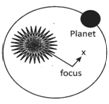
Kepler’s second law
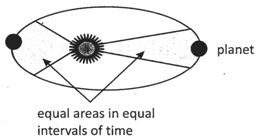
According to second law the line joining planet to the sun sweeps out equal area in equal time interval, as the planet revolve around the sun in a elliptical orbit.
Kepler's Third Law
It states that square of time period is proportional to the cube of its semi major axis.
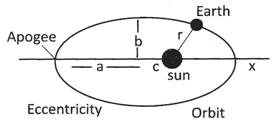
1. Introduction Part 1
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Introduction
→ The energy for the ‘life processes’ comes from food. Activities like playing, singing, reading, w
thinking, jumping, cycling and running requires energy.

1. Introduction Part 1
Work and Energy
Introduction
Work done
Work done on an object is defined as the product of the magnitude of the force acting on the body and the displacement in the direction of the force. W = F.s
If a force acting on a body causes no displacement, the work done is 0. For example, pushing a wall.
Two conditions need to be satisfied for work to be done:
(i) A force should act on object
(ii) The object must be displaced
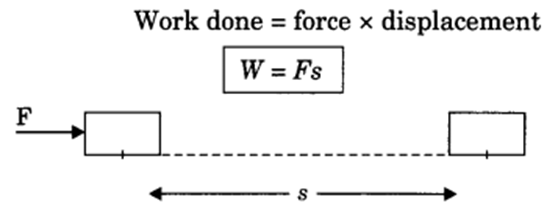
• W = Fs
If F = 1 N and s = 1 m
W= 1 N x 1 Nm
W = 1 Nm
1j =1 Nm
- 1 J is the amount of work done on an object when a force of 1 N displaces it by 1 m along the line of action of the force.
• Work done has only magnitude and no direction i.e., work is a scalar quantity.
• SI unit of work is joule (J).
• 1 joule (one joule)
2. Types of Work
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Work
Work done on an object is defined as the product of the magnitude of the force acting on the body and the displacement in the direction of the force.
W = F.s
If a force acting on a body causes no displacement, the work done is 0. For example, pushing a wall.
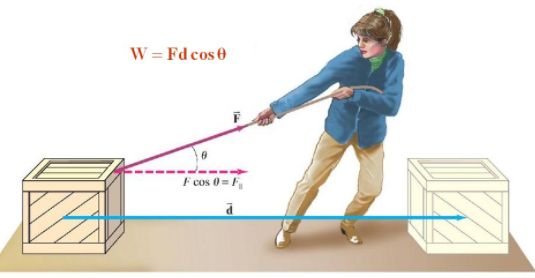
Two conditions need to be satisfied for work to be done:
(i) A force should act on object
(a) The object must be displaced
Work = Force x Displacement
Unit of workdone = Joule = Newton x metre
1 Joule work is said to be done when 1 Newton force is applied on an object and it shows the displacement by 1 meter.

2. Types of Work
Types of work
(i) Zero work: If the angle between force and displacement is 90°, then work done is said to be zero work.
Example: When a man carries a load on his hand and moves on a level road, work done by the man on the load is zero.
(ii) Positive work: Work done is said to be positive if force applied on an object and displacement are in the same direction.
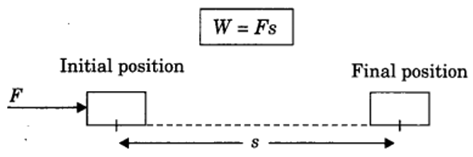
Example: Work done by the force of gravity on a falling body is positive.
(iii) Negative work: Work done is said to be negative if the applied force on an object and displacement are in opposite direction.
W = -Fs
Here displacement is taken to be negative (-s).
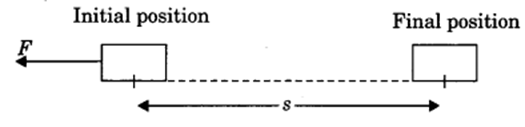
Example: Work done by friction force is usually negative on a moving body.
3. Introduction Part 2
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Energy

Energy is defined as the ability to do work. Its unit is the same as that of work.
SI unit of energy or work = Joule (Nm)
Energy has different forms: Light, heat, chemical, electrical or mechanical.
Mechanical energy is the sum of:
(i) Kinetic energy (K.E)
(ii) Potential energy (P.E)
Kinetic Energy
Objects in motion possess energy and can do work. This energy is called Kinetic Energy.
F = ma.
Also W = F.s
⇒ From the 2nd equation of motion v2−u2=2as,
⇒ we get s = v2−u2 / 2a
Substituting equation for work done by a moving body,
⇒ we get W =m.a * v2−u2 / 2a
Or
⇒ Kinetic Energy = K.E= 1/2 mv2 (taking initial velocity u=0)
When two identical bodies are in motion, the body with a higher velocity has more K.E.
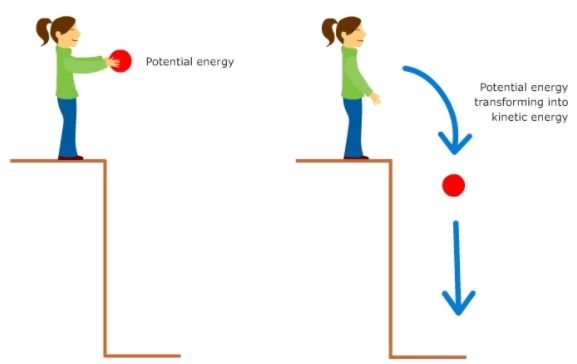
Work-energy theorem
The work-energy theorem states that the net work done by a moving body can be calculated by finding the change in KE.
⇒ Wnet = KEfinal− KEinitial
⇒ Wnet = 1/2 mv2
3. Introduction Part 2
Energy
Energy of a body is defined as the capacity or ability of a body to do work.
The SI unit of energy is joule (J)
Forms of energy
There are various forms of energy in the nature, few of them are mechanical energy (potential energy + kinetic energy) heat energy, chemical energy and light energy.
1. Mechanical energy
Mechanical energy includes kinetic energy and potential energy.
a) Kinetic energy
The energy possessed by a body by the virtue of its motion is called kinetic energy.
Kinetic energy possessed by a body can be calculated by
EK=1/2 mv2
m = mass of body
V = velocity of body
Derivation of kinetic energy
Let us consider an object lying on a frictionless surface having mass ‘m’
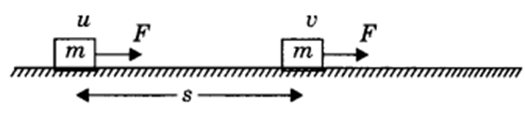
A force of constant magnitude F is acting on the body. Here initial velocity of the body is u and final velocity is v. As there is no dissipative forces, work done on the body will be stored in the form of change in kinetic energy.
W=Fs
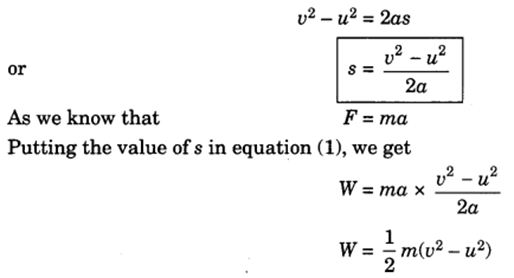
If the object is starting from a stationary position u = 0, then
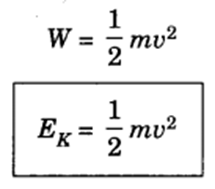
Factors affecting Kinetic energy
• Mass
• Velocity
• Momentum
b) Potential energy
The energy possessed by a body due to its position or configuration is called potential energy.
(i) Gravitational potential energy
Potential energy at any height (h) from a reference can be calculated by formula
Ep = mgh
where, m = mass of object
v = height from reference
The gravitational potential energy of an object at a point above the ground is defined as the work done in raising it from the ground to that point against gravity.
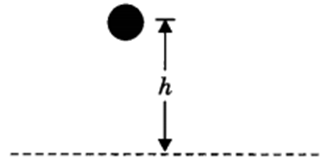
Derivation of potential energy
When work is done on the body, the work is stored in the form of energy. Consider an object of mass, m. Let it be raised through a height, h from the ground. A force is required to do this. The minimum force required to raise the object is equal to the weight of the object, mg. The object gains energy equal to the work done on it. Let the work done on the object against gravity be W.
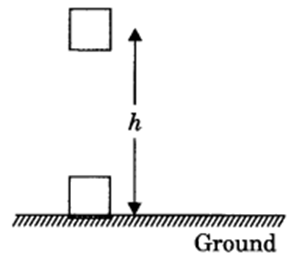
W = force x displacement
= mgh.
Since work done on the object is equal to mgh, an energy equal to mgh units is gained by the object. This is the potential energy (Ep) of the object.
Ep = mgh
WORK ENERGY THEOREM
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Work-energy theorem
The work-energy theorem states that the net work done by a moving body can be calculated by finding the change in KE.
⇒ Wnet = KEfinal− KEinitial
⇒ Wnet = 1/2 mv2
FACTORS AFFECTING K.E.
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Factors affecting kinetic energy
- Mass
- Velocity
- Momentum
POTENTIAL ENERGY
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Potential Energy
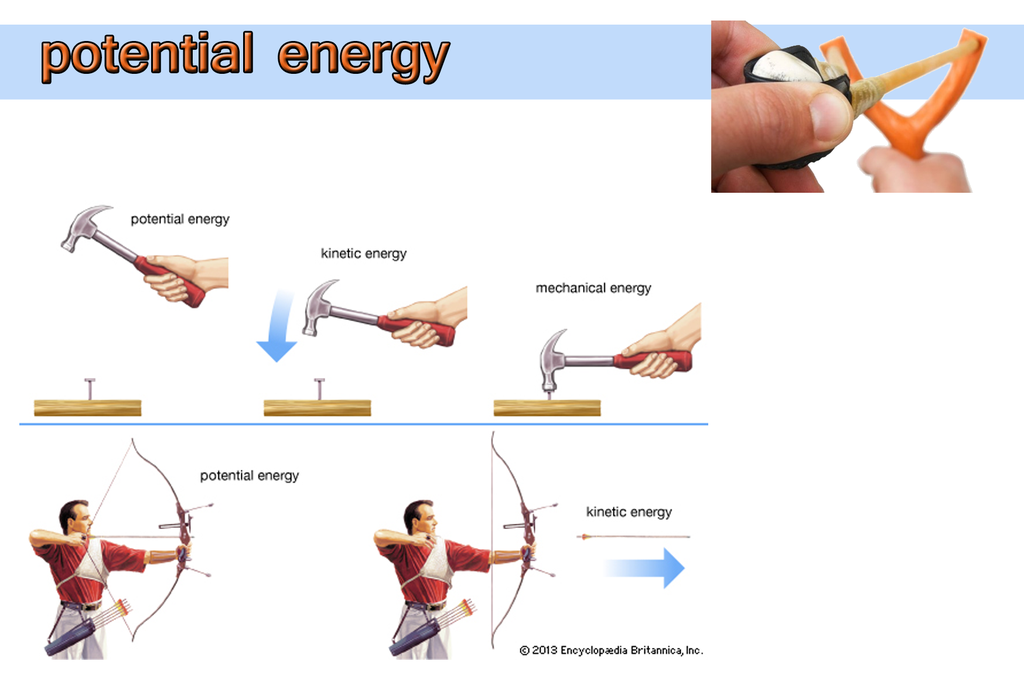
Energy can get stored in an object when work is done on it.
For example, stretching a rubber string. The energy that is possessed by a body by virtue of its configuration or change in position is known as Potential Energy.
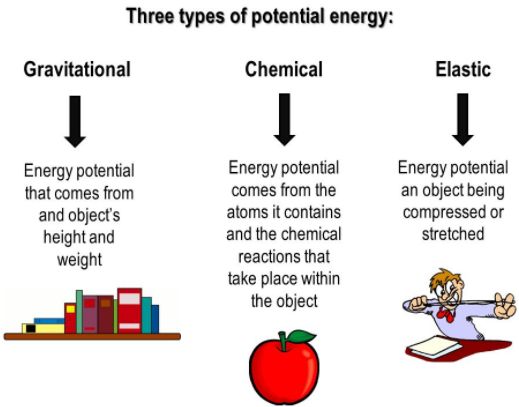
The potential energy of an object at a height.
When an object is raised to a certain height, work is done against gravity to change its position. This energy is stored as Potential Energy.
⇒W = F.s
⇒F = ma
In the case of increasing the height, F = mg
Therefore, W (P.E) = mgh
⇒ ΔPE = mg(hfinal - hinitial )
LAW OF CONSERVATION OF ENERGY
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Law of Conservation of Energy
Law of conservation of energy states that energy can neither be created nor destroyed, but can be transferred from one form to another. The total energy before and after the transformation remains constant.
For example: consider a ball falling freely from a height.
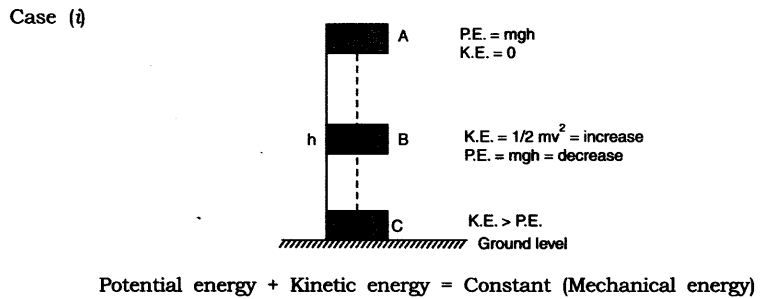
Potential energy + Kinetic energy = Constant (Mechanical energy)
A body of mass ‘m’ is raised to height ‘h’ at A its potential energy is maximum and kinetic energy is 0 as it is stationary.
When body falls at B, h is decreasing hence potential energy decreases and V is increasing hence kinetic energy is increasing.
When the body is about to reach the ground level, h = 0, v will be maximum hence kinetic energy –> potential energy
Decrease in potential energy = Increase in kinetic energy
This shows the continual transformation of gravitational potential energy into kinetic energy.
POWER
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Power
The rate of doing work or the rate of transfer of energy is called power. It is denoted by P
⇒ P = Wt
SI unit is Watt (J/s).
Average power = Total energy consumed / Total time taken
The commercial unit of power is kWh i.e. energy used in 1 hour at 1000 Joules/second.
1KWh = 3.6×106 J
1. Introduction
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Introduction
→ The sensation felt by our ears is called sound.
→ Sound is a form of energy which makes us hear.
→ Law of conservation of energy is also applicable to sound.
→ Sound travels in form of wave.

Production of Sound
→ Sound is produced when object vibrates or sound is produced by vibrating objects.
→ The energy required to make an object vibrate and produce sound is provided by some out
source (like our hand, wind etc.).
→ Example: Sound of our voice is produced by vibration of two vocal cords in our throat.
• Sound of a drum or tabla is produced by vibration of its membrane
when struck.
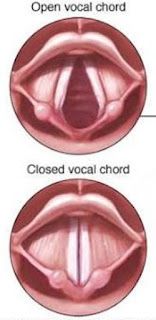
→ In laboratory experiments, sound is produced by vibrating tuning fork. The vibrations of tuning fork
can be shown by touching a small suspended pith ball (cork ball) with a prong of the sounding
tuning fork. The pith ball is pushed away with a great force.

→ In laboratory experiments, sound is produced by vibrating tuning fork. The vibrations of tuning fork
can be shown by touching a small suspended pith ball (cork ball) with a prong of the sounding
tuning fork. The pith ball is pushed away with a great force.
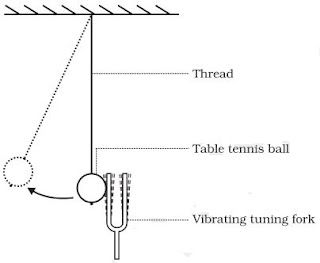
• Sound can be produced by following methods:
(i) By vibrating string (sitar)
(ii) By vibrating air (flute)
(iii) By vibrating membrane (table, drum)
(iv) By vibrating plates (bicycle bell)
(v) By friction in objects
(vi) By scratching or scrubbing the objects etc
1. Introduction
Sound
Introduction
• Sound energy is a form of energy because of which our ears are able to hear something.
• One cannot create sound or destroy it. But one can transform one form of energy into sound energy. For instance, when a cell phone rings, the sound is produced by converting electrical energy into sound energy.
• A wave that is produced when objects of the medium oscillate is called Mechanical Wave. The sound waves are therefore, mechanical waves.
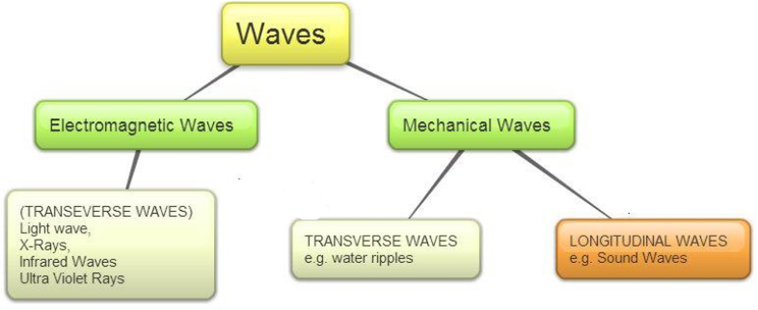
Types of Waves
• Sound cannot travel through the vacuum as it always needs a medium to propagate. The vacuum contains no air hence no particles can propagate sound.
Longitudinal waves - Any wave that vibrates in the direction of the motion is called a Longitudinal Wave. Sound waves are longitudinal because the particles of the medium vibrate in the direction which is parallel to the direction of the propagation of the sound waves. The particles in the medium oscillate to and fro in the case of longitudinal waves.
Transverse Waves - A transverse wave is produced when the particles of the medium oscillate in a direction which is perpendicular to the direction of the propagation of the wave. The particles in a transverse wave oscillate in an up and down motion. For Example, light waves are transverse in nature.
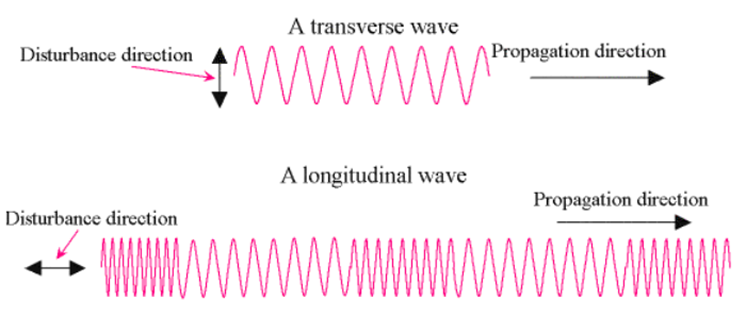
PRODUCTION OF SOUND
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Production of Sound
→ Sound is produced when object vibrates or sound is produced by vibrating objects.
→ The energy required to make an object vibrate and produce sound is provided by some out
source (like our hand, wind etc.).
→ Example: Sound of our voice is produced by vibration of two vocal cords in our throat.
• Sound of a drum or tabla is produced by vibration of its membrane
when struck.
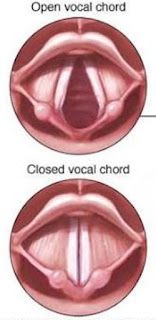
→ In laboratory experiments, sound is produced by vibrating tuning fork. The vibrations of tuning fork
can be shown by touching a small suspended pith ball (cork ball) with a prong of the sounding
tuning fork. The pith ball is pushed away with a great force.

→ In laboratory experiments, sound is produced by vibrating tuning fork. The vibrations of tuning fork
can be shown by touching a small suspended pith ball (cork ball) with a prong of the sounding
tuning fork. The pith ball is pushed away with a great force.
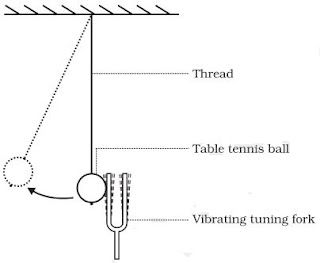
• Sound can be produced by following methods:
(i) By vibrating string (sitar)
(ii) By vibrating air (flute)
(iii) By vibrating membrane (table, drum)
(iv) By vibrating plates (bicycle bell)
(v) By friction in objects
(vi) By scratching or scrubbing the objects etc.
2. Characterstics of Sound
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Propogation of Sound
→ The substance through which sound travels is called a medium.
→ The medium may be solid, liquid or gas.
→ When an object vibrates, then the air particles around it also start vibrating in exactly the same
way and displaced from their stable position.
→ These vibrating air particles exert a force on nearby air particles so they are also displaced from
their rest position and start to vibrate.
→ This process is continued in the medium till sound reaches our ears.
→ The disturbance produced by sound travels through the medium (not the particles of the
medium).
→ Wave is a disturbance which travels through a medium and carries energy.
→ So sound travels in wave form known as mechanical waves.
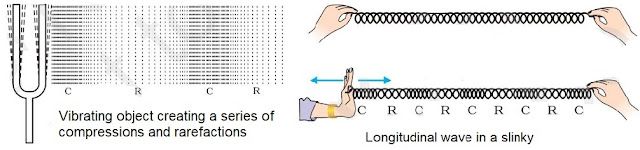
• When a body vibrates then it compresses the air surrounding it and form a area of high density
called compression (C).
→ Compression is the part of wave in which particles of the medium are closer to one another
forming high pressure.
→ This compression move away from the vibrating body.
• When vibrating body vibrates back a area of low pressure is formed called rarefaction (R).
→ Rarefaction is the area of wave in which particles of the medium are further apart from one
another forming a low pressure or low density area.
→ When body vibrates back and forth, a series of compression and rarefaction is formed in air
resulting in sound wave.
→ Propogation of sound wave is propogation of density change.
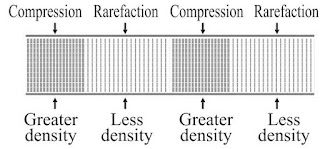
Sound needs Medium for Propogation
• Sound waves are mechanical waves.
→ It needs material medium for propogation like air, water, steel etc.
→ It cannot travel in vaccum.
→ An electric bell is suspended in airtight bell jar connected with vacuum pump.
→ So, medium is necessary for propagation of sound.
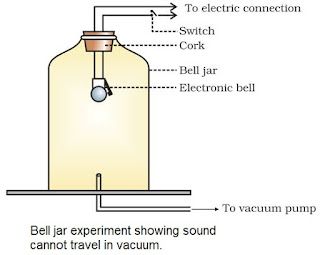
Experiment to show that sound cannot travel through vacuum
2. Characterstics of Sound
Characteristics of Sound
A sound wave is characterized by three factors:
• Amplitude
• Frequency
• Speed
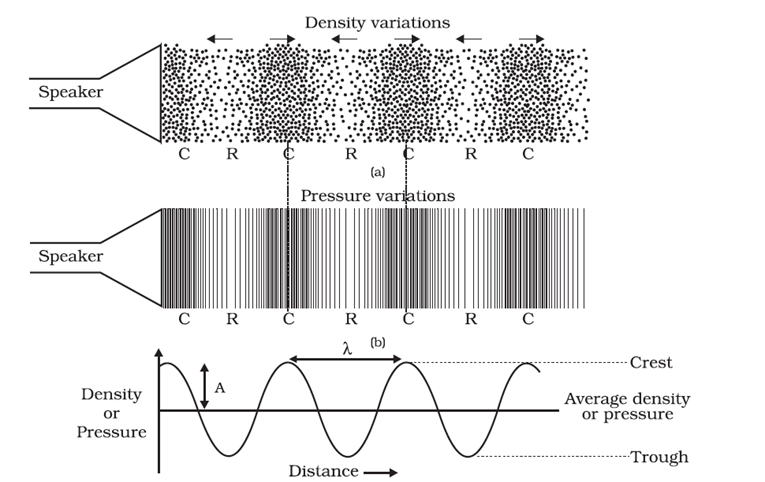
Sound cannot travel at the same speed in different mediums. The speed of sound in a medium is affected by three things:
• The density of the medium. For instance, speed of sound is the maximum through solids
• The temperature of the medium. As the temperature increases, the sound propagates easily.
• Humidity in the air also affects the travel of sound. As the humidity increases, so does the propagation of sound.
Properties of Sound Waves:
Frequency: Number of oscillations of sound waves is called its frequency. The number of peak and troughs per unit of time will give frequency. It is represented by v (nu) and its SI unit is Hertz (Hz).
Time Period: The time taken to complete one oscillation is called its time period. Its unit is second and is represented by T.
Relation of frequency and time period:
v = 1/T
Amplitude: The magnitude of the maximum disturbance in the medium on either side of the mean value is called the amplitude of the wave. It is usually represented by the letter A. Its unit is meter. Softness or Loudness of Sound: If the amplitude is smaller than the sound will be softer and if it is larger than sound will be louder. Higher amplitude helps the sound wave is travelling faster.
Sonic Booms
• When an object travels in the air with a speed greater than that of the sound, it produces a sound with high energy.
• This energy is loud enough that it can break glasses or damage the buildings. The sound produced is similar to the sound of an explosion or thunderclap.
• These objects exert a large amount of pressure on the air which causes the production of shock waves in the air.
• These shock waves produce extremely large and loud sound waves which are called Sonic booms.
• Speed of light in air = 3 * 108 m/s
• Speed of sound in air = 344 m/s
This clearly states that sound travels a lower speed than that of light in air. This is a reason why at the time of lightening, the light is visible instantly while the sound of the thunder reaches our ears after a few seconds.
3. Reflection of Sound and Its Applications
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Sound Waves as Longitudinal Waves
• A wave in which the particles of the medium vibrate back and forth in the same direction in which
the wave is moving, is called a longitudinal wave.
→ When we push and pull the slinky compression (number of turns are more or closer) and
rarefaction (number of turns are less or farther) are formed.
→ When a wave travels along with slinky, its each turn moves back and forth by only a small
distance in the direction of wave. So the wave is longitudinal.
→ The direction of vibrations of the particles is parallel to the direction of wave.

• When one end of a slinky is moved up and down rapidly whose other end is fixed, it produces
transverse wave.
→ This wave possess along the slinky in horizontal direction, while turns of slinky (particles) vibrates
up and down at right angle to the direction of wave.
→ Thus in transverse wave particles of the medium vibrate up and down at right angles to the
direction of wave.
→ Light waves are transverse waves but they don’t need a material
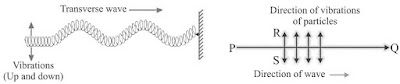
3. Reflection of Sound and Its Applications
Laws of reflection
• The incident sound wave, the reflected sound wave and the normal, all lie in the same plane.
• The angle of incident of incident sound wave is equal to the angle of reflection formed by the reflected sound wave, that is, i = r
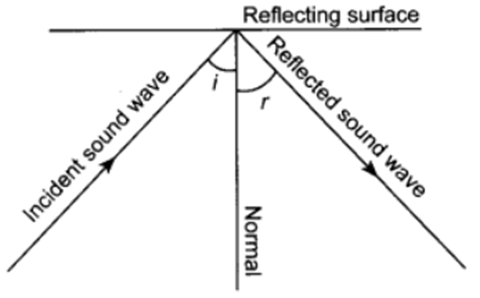
Echo
• When we hear the same sound again and again in a medium it is called Echo.
• The sound or echo persists in our brain for 0.1 seconds. This means that the difference between sound and its echo should be at least 0.1 seconds.
• It is produced as a result of reflection of sound through a medium. If sound reflects more than once we may hear multiple echoes.
Reverberation: Repeated reflections of sound results in persistence of sound and is called reverberation.
Use of Reverberation of Sound: Following instruments use this property of sound:
1. Megaphones, Shehanais, Trumpets
2. Stethoscope
3. Curved dome of concert halls
Advantages of Multiple Reflection of Sound
• Horns, trumpets, loudhailers or megaphones are designed in such a way that sound can travel in a particular direction only without spreading out everywhere. This makes it easier for the audience to listen to the speaker. All these instruments work on the phenomena of multiple reflections of sound.
• The multiple reflections in a stethoscope tube make it possible for the doctors to listen to a patient’s heartbeat.
• Concert halls are generally covered so that sound can reflect through it and reach the wider audience.
• Human auditory range is between 20 Hz and 20000 Hz.
4. Ultrasound's and its Application
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Characteristics of Sound Wave
• The characteristics of sound waves are : wavelength, frequency, amplitude, time period and
velocity.
→ When a wave travel in air the density and pressure of air changes from their mean position.
→ Compression is shown by crest while rarefaction is shown by trough.
→ Compression is the region of maximum density or pressure.
→ Rarefaction is the region of minimum density or pressure.
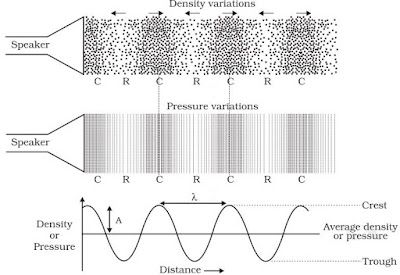
Wavelength
→ In sound waves the combined length of a compression and an adjacent rarefaction is called
wavelength.
→ The distance between the centres of two consecutive compressions or two consecutive
rarefactions is also called its wavelength.
→ It is denoted by the Greek letter lamda (λ). Its SI unit is metre.
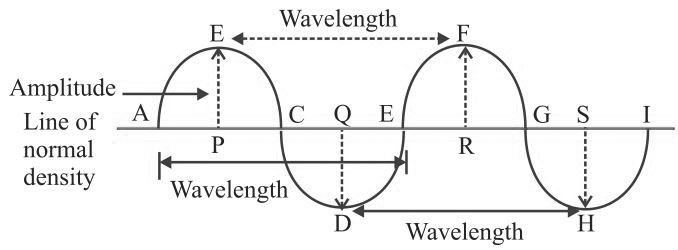
Frequency
→ No. of complete waves produced in one second or number of vibrations per second is called
frequency.
→ Number of compressions or rarefactions passed in one second is also frequency.
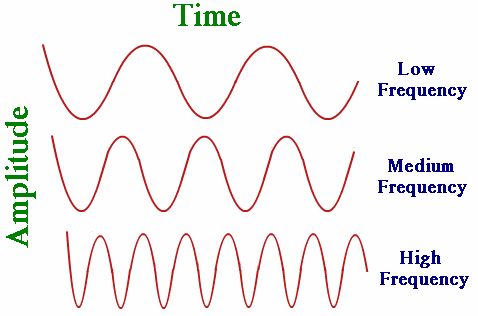
→ Frequency of wave is same as the frequency of the vibrating body which produces the wave
• The SI unit of frequency is hertz (Hz). The symbol of frequency is v (nu).
• 1 Hertz: One Hz is equal to 1 vibration per second.
• Bigger unit of frequency is kilohertz kHz = 1000 Hz.
Time Period
→ Time taken to complete one vibration is called time period.
→ Time required to pass two consecutive compressions or rarefactions through a point is called
time period.
• SI unit of time period is second (s). Time period is denoted by T.
• The frequency of a wave is the reciprocal of the time period.
• v = 1/T
Amplitude
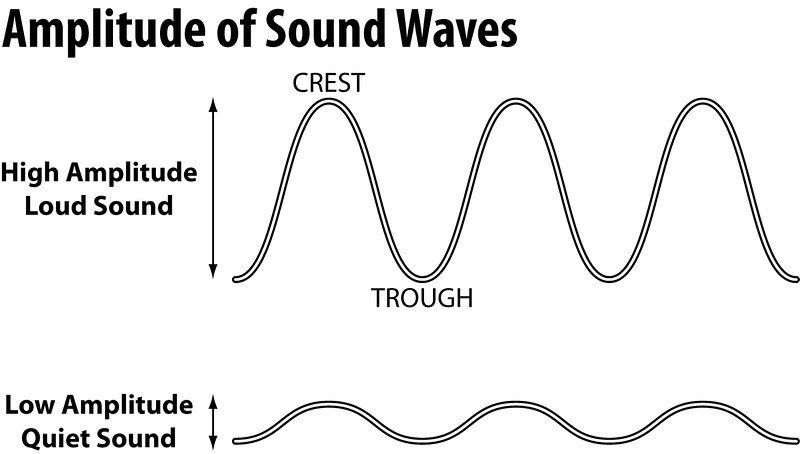
→ The maximum displacement of the particle of the medium from their original undisturbed
position is called amplitude of the wave.
• Amplitude is denoted by A and its SI unit is metre (m).
→ Sound have characteristics like pitch and loudness and timbre.
• Pitch: The pitch of sound depends on the frequency of sound (vibration).
→ It is directly proportional to its frequency. Greater the frequency, higher is the pitch and lesser the
frequency, lower is the pitch.
→ A woman’s voice is shrill having a high pitch while a man’s voice is flat having low pitch.
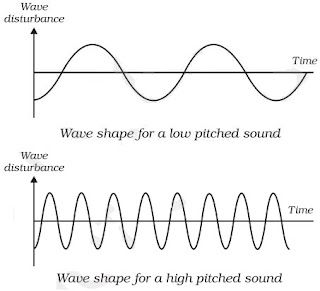
• Loudness: The loudness depends on the amplitude of the sound wave.
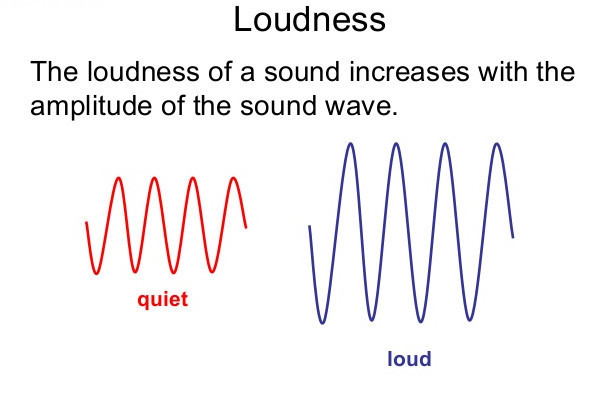
→ Loudness is the measure of the sound energy reaching the ear per sec.
→ Greater the amplitude of sound wave, greater is the energy, louder the sound; short is the
amplitude, less is the energy, soft is the sound.
→ Loudness is measured in decibel ‘dB’.
• Quality or Timbre: The timbre of a sound depends on the shape of sound wave produced by
the characteristic of musical sound.
→ It helps us to distinguish between two sounds of same pitch & loudness.
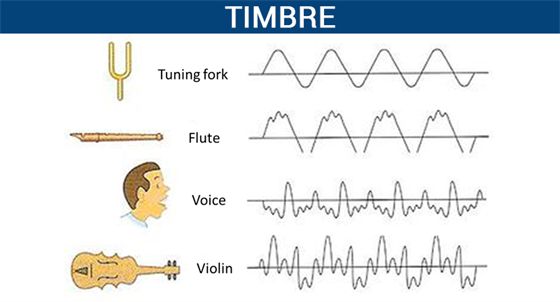
• Sound of single (same) frequency is called tone while a mixture of different frequencies is called
note.
• The distance travelled by a wave in one second is called velocity of the wave.
• Its SI unit is metre per second (m/s ).
Velocity = Distance travelled/Time taken
⇒ v = λ/T
(λ is the wavelength of the waves travelled in one time time period T)
v = λv (1/T = v)
So, Velocity = Wavelength × Frequency
This is the wave equation.
Example: What is the frequency of sound wave whose time period is 0.05 second ?
4. Ultrasound's and its Application
Ultra Sound
The ultrasound waves are the sound waves with high frequency. Due to this, they can travel long distances despite any obstacles between their paths.
Application of Ultra Sound
• The ultrasound waves are used in clearing parts of objects that are hard to reach such as a spiral tube or electronic components. In order to clean the objects, they are put in a solution, then the ultrasonic waves are passed through the solution. As a result, the dust particles on the object get detached and fall off them.
• Ultrasound waves can recognize tiny cracks in metallic objects that are used in the manufacture of large structures, buildings and scientific equipment. The presence of such cracks can lower the strength of these structures and machines. Hence, the ultrasound waves are passed through the metallic objects and detectors are used to detect the waves that pass through the cracks. If a crack is present the ultrasound waves would reflect back.
• Ultrasonic waves are also used in a medical process called Echocardiography. In this process, the ultrasound waves are passed through various parts of the heart in order to form the images of the organ.
• Ultrasonic waves are also used in a procedure called Ultrasonography. In this procedure, the ultrasonic waves are passed through the internal organs of the body in order to get their image. In this way, the doctors can find out the cause of a disease or any abnormalities in the organs. The ultrasound waves travel through the tissues of the body and as soon as the density of the tissue changes, they reflect back. The reflected waves are then converted into electrical signals which form the images of the internal organs.
• Ultrasound waves are also used to break the kidney stones.
SONAR – Sound Navigation and Ranging
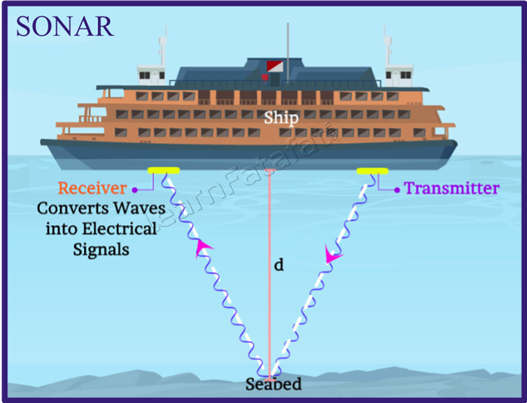
• This device is used to find the distance, direction and speed of objects that are present under the water. It uses Ultrasonic waves to do so.
• The Sonar consists of two main devices – The transmitter and the detector (or receiver). The main function of the transmitter is the production and transmission of the Ultrasonic waves in water.
• As these waves travel underwater, they, when hit by an object, reflect back to the detector. The detector then converts these sound waves into electrical signals which are then interpreted.
• The distance of the object is calculated with the help of the speed of sound in water and time taken by the way to reach the detector. This process is called Echo Ranging.
Uses of Sonar
• Finding the depth of a water body such as sea
• Detecting the presence of underwater objects like submarines, hills, icebergs and ships
The Human Ear
The ear is a sensitive organ of the human body. It is mainly involved with detecting, transmitting and transducing sound and maintaining a sense of balance is another important function of the human ear. Human ear includes:
• The outer ear or the visible part of the ear is called the pinna.
• Pinna collects sound from the surroundings.
• Sound passes through a tube called an auditory canal.
• Eardrum (tympanic membrane) vibrates in response to incident sound waves.
• Vibrations are amplified and transmitted further by three bones hammer, anvil and stirrup in the middle ear to the inner ear.
• In the inner ear, cochlea converts pressure signals into electrical signals.
• Electrical signals are transmitted by the auditory nerve to the brain for interpretation.
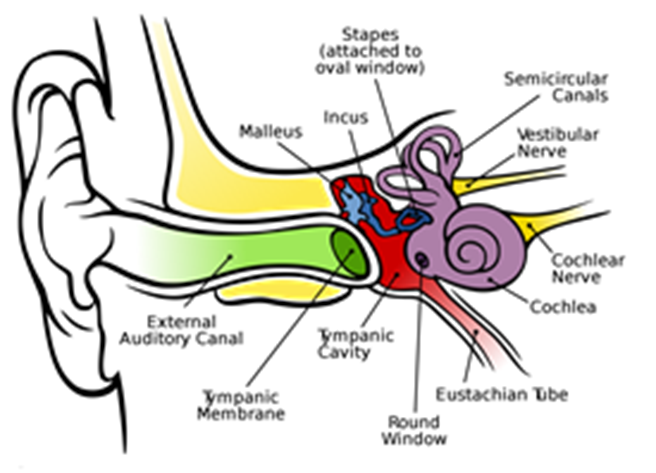
Structure of Human Ear
5. Applications Of Ultrasound
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Speed of Sound in Various Mediums
→ Speed of sound depends on the nature of material through which it travels. It is slowest in gases,
faster in liquids and fastest in solids.
→ Speed of sound increases with the rise in temperature.
→ Speed of sound increases as humidity of air increases.
→ Speed of light is faster than speed of sound.
→ In air, speed of sound is 344 ms-1 at 22ºC.
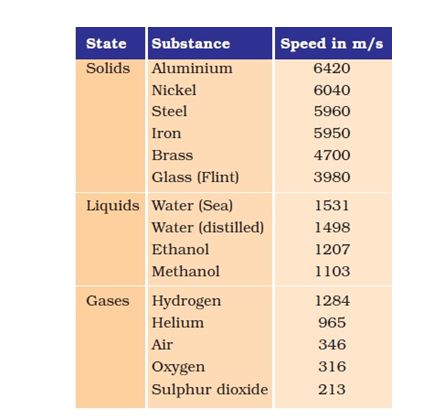
Sonic Boom
→ Some aircrafts, bullets, rockets etc. have ‘supersonic speed’.
• Supersonic refers to the speed of an object which is greater than the speed of sound and it
produces extremely loud sound waves called ‘shock waves’ in air.

Reflection of Sound
→ Like light, sound also bounce back when it falls on a hard surface. It is called reflection of sound.
• The laws of reflection of light are obeyed during reflection of sound.
(i) The incident sound wave, the reflected sound wave and normal at the point of incidence lie
same plane.
(ii) Angle of reflection of sound is always equal to the angle of incidence of sound.
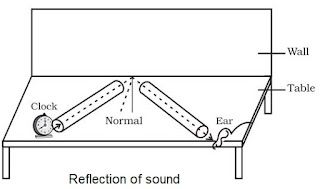
SONIC BOOM
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Sonic Boom
→ Some aircrafts, bullets, rockets etc. have ‘supersonic speed’.
• Supersonic refers to the speed of an object which is greater than the speed of sound and it
produces extremely loud sound waves called ‘shock waves’ in air.

REFLECTION OF SOUND
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Reflection of Sound
→ Like light, sound also bounce back when it falls on a hard surface. It is called reflection of sound.
• The laws of reflection of light are obeyed during reflection of sound.
(i) The incident sound wave, the reflected sound wave and normal at the point of incidence lie
same plane.
(ii) Angle of reflection of sound is always equal to the angle of incidence of sound.

6. Structure Of Human Ear
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Echo
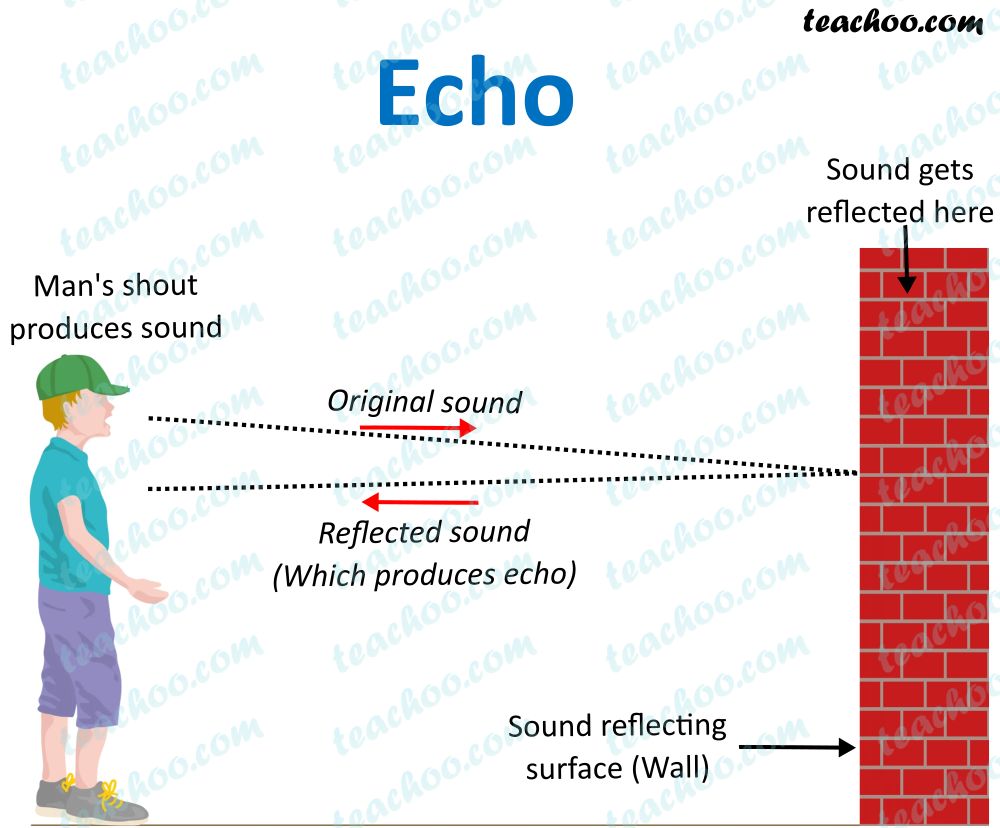
• The repetition of sound caused by the reflection of sound waves is called an echo.
→ We can hear echo when there is a time gap of 0.1 second in original sound and echo (reflection of
sound).
→ Echo is produced when sound reflected from a hard surface (i.e. brick wall, mountain etc.) as
surface tends to absorb sound.
Minimum distance to hear an echo
Speed = Distance/Time
Here, Speed of sound in air = 344 ms -1 at 22ºC
Time = 0.1 second
344 = Distance/0.1 sec
⇒ Distance = 344 × 0.1 = 34.4 m
So, distance between reflecting surface and audience = 34.4/2 = 17.2 (at 22ºC).
Reverberation
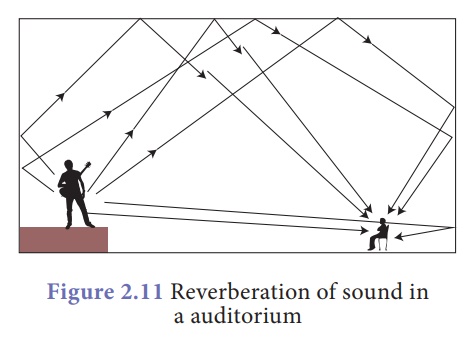
• The persistence of sound in a big hall due to repeated reflection of sound from the walls, ceiling
and floor of the hall is called reverberation.
→ If reverberation is too long, sound becomes blurred, distorted and confusing due to overlapping
of different sound.
Methods to reduce reverberation in big halls or auditoriums
→ Panels made of felt or compressed fibre board are put on walls and ceiling to absorb sound
→ Heavy curtains are put on doors and windows.
→ Carpets are put on the floor.
→ Seats are made of material having sound absorbing properties.
APPLICATIONS OF REFLECTION OF SOUND
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Applications of Reflection of Sound
(i) Megaphone, loudspeakers, bulb horns and trumpets, shehnai etc. are designed to send sound to
a particular direction without spreading all around.
→ All these instruments have funnel tube which reflects sound waves repeatedly towards audio
In this amplitude of sound waves adds up to increase loudness of sound.
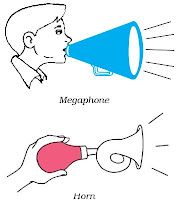
(ii) Stethoscope: It is a medical instrument used for listening the sounds produced in human bo
mainly in heart and lungs. The sound of the heartbeats reaches the doctor’s ears by the multipe
reflection of the sound waves in the rubber tube of stethoscope.
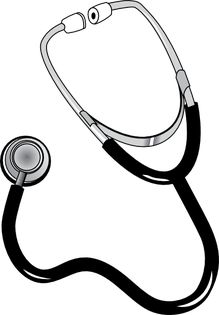
(iii) Sound Board: In big halls or auditoriums sound is absorbed by walls, ceiling, seats etc. So a
curved board (sound board) is placed behind the speakers so that his speech can be heard ea
by audiences. The soundboard works on the multiple reflection of sound.
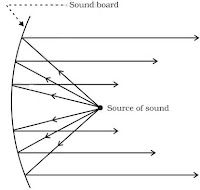
(iv) The ceiling of concert halls are made curved, so that sound after reflection from ceiling, rea
all the parts of the hall.
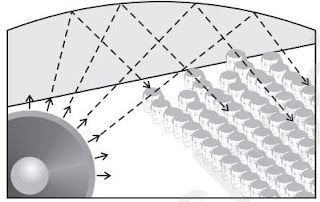
RANGE OF HEARING
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Range of Hearing
(i) Range of hearing in human is 20 Hz to 20000 Hz.
→ Children younger than 5 years and dogs can hear upto 25 Khz.
(ii) The sounds of frequencies lower than 20 Hz are
known as ‘infrasonic sounds’
→ A vibrating simple pendulum produces infrasonic sounds.
→ Rhinoceroses communicate each other using frequencies as low as 5 Hz.
→ Elephants and whales produces infrasonic waves.
→ Earthquakes produces infrasonic waves (before shock waves)
which some animals can hear and get disturbed.
(iii) The sounds of frequencies higher than 20 KHz are known as ‘ultrasonic waves’.
→ Dogs, parpoises, dolphins, bats and rats can hear ultrasonic sounds.
→ Bats and rats can produce ultrasonic sounds.
Hearing Aid
→ It is battery operated electronic device used by persons who are hard of hearing.
→ Microphone convert sound into electrical signals, than those are amplified by amplifier. Ampified
signals are send to the speaker of hearing aid. The speaker converts the amplified signal to sound
and sends to ear for clear hearing.
Applications of Ultrasound
(i) It is used to detect cracks in metal blocks in industries without damaging them.
(ii) It is used in industries to clean ‘hard to reach’ parts of objects such as spiral tubes, odd shaped
machines etc.
(iii) It is used to investigate the internal organs of human body such as liver, gall bladder, kidney
uterus and heart.
(iv) Ecocardiography: These waves are used to reflect the action of heart and its images are
formed. This technique is called echocardiography.
(v) Ultrasonography: The technique of obtaining pictures of internal organs of the body by using
echoes of ultrasound waves is called ultrasonography.
(vi) Ultrasound is used to split tiny stones in kidneys into fine grains.
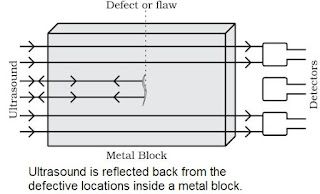
SONAR
→ The word ‘SONAR’ stands for ‘Sound Navigation And Ranging’.
→ SONAR is a device which is used to find distance, direction and speed of underwater objects
→ SONAR consists of a transmitter and a receptor or detector and installed at the bottom of a sea
→ The transmitter produces and transmits ultrasonic waves.
→ These waves travel through water and after striking the objects on the bottom of sea, are
reflected back and received by detector.
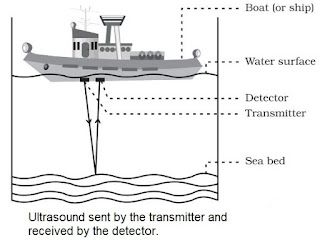
→ These reflected waves are converted into electric signals by detector.
→ The sonar device measures the time taken by ultrasound waves to travel from ship to bottom of
sea and back to ship.
→ Half of this time gives the time taken by the ultrasound waves from ship to bottom.
• Let the time interval between transmission and reception of ultrasound signal is t.
Speed of sound through sea water is v
Total distance travelled by waves = 2d.
→ The sonar is used to find the depth of sea, to locate underwater hills, valleys, submarines, ice
and sunken ships etc.
→ Bats fly in the dark night by emitting high pitched ultrasound waves which are reflected from
obstacle or prey and returned to bats ear.
→ The nature of reflection tells the bat where the obstacle or prey is and what it is like.
HUMAN EAR
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Structure of Human Ear
→ The ear consists of three parts: outer ear, middle ear and inner ear.
→ The ears are the sense organs which help us in hearing sound.
→ The outer ear is called pinna. It collects the sound from surroundings.
→ This sound passes through the auditory canal.
→ At the end of auditory canal, is a thin elastic membrane called ear drum or tympanic memb
→ The middle ear contains of three bones: hammer, anvil and stirrup linked with one another. F
end of hammer touches ear drum and that of stirrup linked with membrane of oval window of
ear.
→ The lower part of middle ear has a narrow ‘Eustachian tube’.
→ The inner ear has a coiled tube called cochlea, which is connected with oval window. Cochle
filled with a liquid containing nerve cells.
→ Other side of cochlea is connected to auditory nerve which goes to brain.
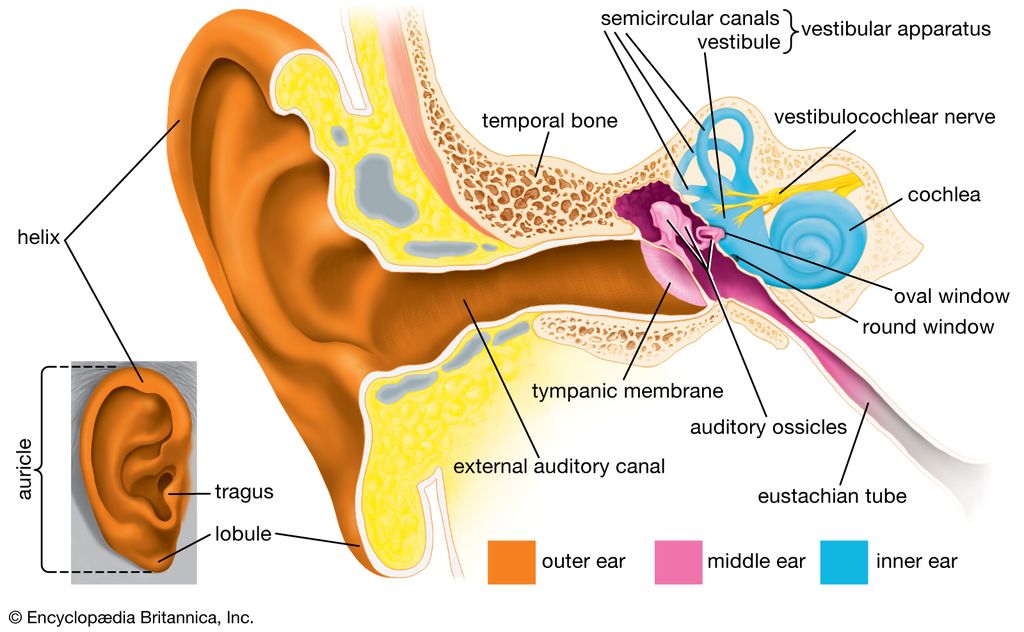
Working of Human ear
Pinna → Ear canal → Ear drum → Hammer → Anvil → Stirrup → Oval window → Cochlea → Audi
nerve → Brain
→ When compression of sound wave strikes the ear drum, the pressure on the outside of ear d
increases and pushes the ear drum inwards.
→ While during rarefaction ear drum moves outwards. Thus, ear drum starts vibrating back an
forth.
→ These vibrations are increased by three bones and middle ear transmits these amplified pre
variations received from sound waves to inner ear.
→ In the inner ear the pressure variations are turned into electric signals by the cochlea.
→ These electric signals are sent to the brain via auditory nerve and the brain interprets them
sound.
4. Law of Conversation of Energy
Law of Conservation of Energy
Energy can neither be created nor destroyed, it can only be transformed from one form to another. The total energy before and after transformation remains the same.
Total energy = KE + PE
For example: consider a ball falling freely from a height. At height h, it has only PE = mgh.
By the time it is about to hit the ground, it has a velocity and therefore has KE=
mv2. Therefore, energy gets transferred from PE to KE, while the total energy remains the same.
Power (P)
Power is defined as the rate of doing work or rate of transfer of energy.
Power = work/time
P=W/T
• Unit of power is watt (W).
Watt
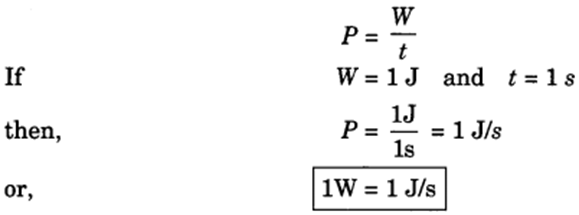
Commercial unit of energy
• Kilowatt hour (kWh) or 1 unit
• The energy used in households, industries and commercial establishments are usually expressed in kilowatt hour.
• 1 kWh is the energy used in one hour (1 h) at the rate of 1000 J/s or (1 kW).
∴1 kWh =l kW x U = 1000 W x 3600 s = 3600000 J
1 kWh = 3.6 x 106 J = 1 unit
Power can also be represented as,
P = Fv
F = force applied
v = velocity of object
P=W/t=Fs/t=Fv

 Science Made Easy
Science Made Easy
 ACERISE INDIA
ACERISE INDIA
